Свойства числовых характеристик(мат ожидание, дисперсия).

Мат ожидание:

1. Математическое ожидание постоянной величины равно самой постоянной:

M(C)=C

Д-во: Будем рассматривать постоянную С как дискретную случайную величину, которая имеет одно возможное значения С и принимает его с вероятностью р=1. М(С)=С*1=С.

2.  Постоянный множитель можно выносить за знак математического ожидания: М(СХ)=СМ(Х)

 Д-во: Пусть случайная величина Х задана законом распределения вероятностей:

Х	x1	x2	…	xn
p	p1	p2	…	pn

 или

СХ	Сx1	Сx2	…	Сxn
p	p1	p2	…	pn

 Математическое ожидание случ. величины СХ:

 M(CX)=Cx1p1+Cx2p2+…Cxnpn=C(x1p1+x2p2+…xnpn)=CM(X) => M(CX)=CM(X).

3. Математическое ожидание произведения двух независимых случ. величин равно произведению их мат ожиданий. M(XY)=M(X)M(Y)

Д-во: Пусть независимы случайные величины Х и Y заданы своими законами распределения вероятностей:

 

 

X	x1y1	Y	y1y2
p	p1p2	g	g1g2

 

Составив все значения, которые может принимать случ. величина XY, напишем закон распределения XY.

ХY	x1y1	x2y1	x1y2	x2y2
p	p1g1	p2g1	p1g2	p2g2

Мат ожидание равно сумме произведений всех возможных значений на их вероятности:

M(XY)=x1y1*p1g1+x2y1*p2g1+x1y2*p1g2+x2y2*p2g2=y1g1(x1p1+x2p2)+y2g2(x1p1+x2p2)=

=(x1p1+x2p2)(y1g1+y2g2)=M(X)M(Y).

Следствие:

M(XYZ)=M(X)M(Z)M(Y)

4. Мат ожидание суммы двух случ величин равно сумме мат ожиданий слагаемых:

M(X+Y)=M(X)+M(Y)

Д-во: Пусть случ величины X и Y заданы следующими законами распределения:

X	x1	x2	Y	y1	y2
p	p1	p2	g	g1	g2

Составим все возможные значения величины X+Y: x1+y1; x2+y1; x1+y2; x2+y2. Обозначим их вероятности соответственно p11, p12, p21 и p22. Мат ожидание X+Y равно:

M(X+Y)=(x1+y1)p11+(x1+y2)p12+(x2+y1)p21+(x2+y2)p22=x1(p11+p12)+x2(p21+p22)+

+y1(p11+p21)+y2(p12+p22).

p11+p12=p, т.к. Событие «Х примет значение х1» влечет за собой событие «Х+Y примет значения x1+y1 или x1+y2», вероятность которого равно p11+p12. Следовательно, p11+p12=p1.

Аналогично: p21+p22=p2; p11+p21=g1 и p12+p22=g2. Получим:

M(X+Y)=(x1p1+x2p2)+(y1g1+y2g2)=M(X)+M(Y)

Следствие: M(X+Y+Z)=M(X)+M(Y)+M(Z)

Дисперсия:

1. D(C)=0;

Д-во: D(C)=M{[C-M(C)]²}=M[(C-C)²]=M(0)=0.

2. D(CX)=C²D(X)

Д-во: D(CX)=M{[CX-M(CX)]²}= M{[CX-CM(X)]²}=M{C²[X-M(X)]²}=C²M{[X-M(X)]²}=C²D(X).

3. D(X+Y) =D(X)+D(Y).

Д-во: D(X+Y) = M[(X+Y)²]-[M(X+Y)]²= M[X²+2XY++Y²]-[M(X)+M(Y)]²=M(X²)+2M(X)M(Y)+

+M(Y²)-M²(X)-2M(X)M(Y)-M²(Y)={ M(X²)-[M(X)]²}+{ M(Y²)-[M(Y)]²}=D(X)+D(Y).

Следствие 1: D(X+Y+Z)=D(X)+D(Y)+D(Z)

Следствие 2: D(C+X)=D(X)+D(C)=D(X)

4. D(X-Y)=D(X)+D(Y)

Д-во: D(X-Y)=D(X)+D(-Y)=D(X)+(-1)²D(Y)=D(X)+D(Y)

 

Нормальное распределение.

Нормальным называют распределение вероятностей непрерывной случ величины, которое описывается плотностью:

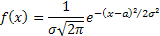
где a-мат ожидание, а σ – среднее квадратическое отклонение Х.

1. D(f)=R

2.

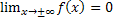
3.

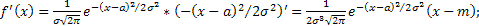
4.

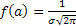
Вероятность того, что Х примет значение, принадлежащее интервалу (α,β)

P(α<X<β)=Ф((β-a)/σ)-Ф((α-a)/σ), где 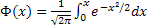 – функция Лапласа.

1. Ф(-∞)=0

2. Ф(+∞)=1

3. Ф(-х)=1-Ф(х)

P(mx-l<x<mx+l)=Ф(l/σ)-Ф(-l/σ)=2Ф(l/σ)-1

Асимметрия, эксцесс, мода и медиана нормального распределения соответственно равны:

As=0, Ek=0, M0=a, Me=a, где a=M(x).

 

Правило «трех сигма».

Если случайная величина распределена нормально, то абсолютная величина ее отклонения от мат ожидания не превосходит утроенного среднего квадратического отклонения.

 

Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:

 

 

       Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:

 

 

 

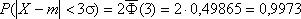
       Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.

 

       Это правило называется правилом трех сигм.

 

Равномерное распределение

На практике очень часто встречаются случ числа, про которые заранее известно, чтоих значения лежат в пределах некоторого интервала, и все значения случ величины одинаково вероятны.

О таких случ числах говорят, что они распределены равномерно. Плотность такого распределения сохраняет постоянное значение, а именно f(x)=1/(b-a). Вне этого интервала f(x)=0.

Вероятность попадания значения случ числа в заданный интервал (a;b), можно вычислить по формуле: .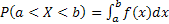

График плотности равомерного распределения симметричен относительно прямой x=(a+b)/2, поэтому M(x)=(a+b)/2. Этот же результат можно получить по формуле .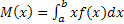

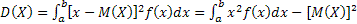. Подставив формулы, полученные выше, получим D(x)=(b-a)²/12. В таком случае среднее квадратическое отклонение случ числа равно .

 

 

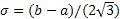Закон Пуассона.

Рассмотрим дискретную случ величину Х, которая может принимать целые неотрицательные значения. Говорят, что случ величина распределена по закону Пуассона, если вероятность того, что она примет значение m, выражена формулой: 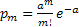 , где a – параметр Пуассона.

Доказательство:

                                     

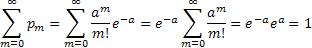
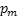
                                                                 x 

      

/

/

.

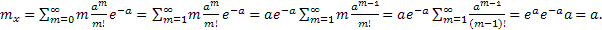
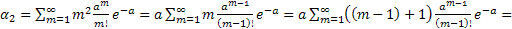
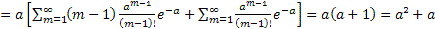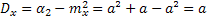Равенство мат ожидания и дисперсии параметру а используется на практике для решения вопроса правдоподобия гипотезы о том, что случ величина Х распределяется по закону Пуассона.

Пусть на оси абсцисс случ образом распределены точки. Допустим, что случ образом распределенные точки удовлетворяют следующим условиям:

1. Вероятность попадания того или иного числа точек на отрезок l зависит от их положения на оси абсцисс.

2. Точки распределяются по оси абсцисс независимо друг от друга.

3. Вероятность попадания на малый участок ∆х 2х и более точек пренебрежимо мала по сравнению с вероятностью попадания одной точки.

Выделим отрезок длины l и рассмотрим дискретную случ величину Х числа точек, попадающих на этот отрезок.

Докажем, что случ величина Х подчиняется закону Пуассона и посчитаем вероятность того, что на этот отрезок попадет ровно m точек. Рассмотрим маленький участок этой прямой ∆х и вычислим вероятность того, что на этот участок попадет хотя бы одна точка.

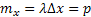
Согласно 3му условию вероятность попадания на участок ∆х 2 и более точек ≈0, поэтому мат ожидание будет = вероятности попадания хотя бы одной точки на ∆х.

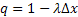
       Для вычисления вероятности попадания на отрезок l ровно m точек, разделим этот участок на n частей: ∆х = l/n, p=λ∆x=λl/n, q=1-(λl/n).

По условию 2 вероятности попадания точек являются независимыми можно использовать частную теорему повторения опыта:

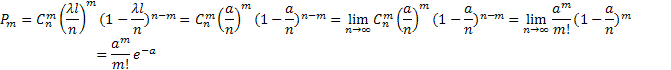
Параметр a определяется как ср. число точек, попадающих на нужный отрезок.