Вязкой жидкости
Полученное уравнение Бернулли (6.2) справедливо для идеальной жидкости, вязкость которой равна нулю.
Для того чтобы распространить это уравнение на реальную жидкость необходимо уравнение Бернулли записать для двух сечений элементарной струйки. При движении вязкой жидкости между движущимися частицами возникает сила трения, в результате чего часть механической энергии перейдет в теплоту. Если жидкость движется с малой скоростью, то это тепло не повышает температуру. Так как часть механической энергии перешла в теплоту, поэтому
 ,[Дж/кг]. (6.3)
,[Дж/кг]. (6.3)
Разделив уравнение (6.3) на g, получим уравнение Бернулли в единицах напора
 , [м]. (6.4)
, [м]. (6.4)
Если разделим уравнение (6.4) на  , получим уравнение Бернулли в единицах давления
, получим уравнение Бернулли в единицах давления
 , [Па], (6.5)
, [Па], (6.5)
где  соответственно потери удельной энергии, напора и давления на преодоление гидравлических сопротивлений. Сопротивления бывают двух типов:
соответственно потери удельной энергии, напора и давления на преодоление гидравлических сопротивлений. Сопротивления бывают двух типов:
1. Гидравлические сопротивления, которые возникают за счет трения по всей длине канала ( );
);
2. Гидравлические сопротивления, которые возникают внезапно при изменении диаметра трубопровода, наличии поворота, колена, клапана, задвижки и т.д. Их называют местными сопротивлениями ( ).
).
Общие гидравлические потери получают путем суммирования всех имеющихся сопротивлений. Тогда

Итак, уравнение Бернулли имеет три формы записи, поэтому рассмотрим смысл каждого уравнения в отдельности.
1. Уравнение Бернулли, записанное в форме (6.3), представляет собой закон сохранения механической энергии, отнесенной к единице массы, поэтому каждое слагаемое несет следующий смысл:
 – удельная потенциальная энергия положения, [Дж/кг];
– удельная потенциальная энергия положения, [Дж/кг];
 – удельная потенциальная энергия давления, [Дж/кг];
– удельная потенциальная энергия давления, [Дж/кг];
 – удельная кинетическая энергия;
– удельная кинетическая энергия;
 – удельная полная механическая энергия;
– удельная полная механическая энергия;
 – потери удельной механической энергии.
– потери удельной механической энергии.
2. Уравнение Бернулли, записанное в форме (6.4), представляет собой закон сохранения полного давления, где  – статическое давление,
– статическое давление,  – динамическое давление,
– динамическое давление,  – полное гидростатическое давление.
– полное гидростатическое давление.
3. Уравнение Бернулли, записанное в форме (6.5), представляет собой закон сохранения полного гидродинамического напора и поэтому несет геометрический смысл. В этом смысле имеет место теорема Бернулли: при стационарном движении тяжелой идеальной несжимаемой жидкости гидравлическая высота, равная сумме скоростной, пьезометрической и геометрической высот, сохраняет постоянное значение вдоль любой линии тока (траектории) или вихревой линии (рис. 6.1).


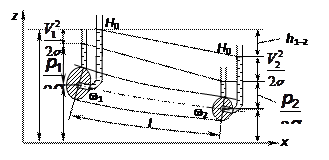
Рис. 6.1. Геометрический смысл слагаемых уравнения Бернулли
Выделим в потоке элементарную струйку, проведем два сечения (1-1, 2-2), тогда каждое слагаемое будет иметь следующий смысл:
 – нивелирная (геометрическая) высота;
– нивелирная (геометрическая) высота;
 – пьезометрическая высота;
– пьезометрическая высота;
 – пьезометрический напор;
– пьезометрический напор;
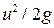 – скоростной (динамический) напор;
– скоростной (динамический) напор;
 – полный гидродинамический напор [м];
– полный гидродинамический напор [м];
 – потери напора на участке 1-2.
– потери напора на участке 1-2.



 ,[Дж/кг]. (6.3)
,[Дж/кг]. (6.3) , [м]. (6.4)
, [м]. (6.4) , получим уравнение Бернулли в единицах давления
, получим уравнение Бернулли в единицах давления , [Па], (6.5)
, [Па], (6.5) соответственно потери удельной энергии, напора и давления на преодоление гидравлических сопротивлений. Сопротивления бывают двух типов:
соответственно потери удельной энергии, напора и давления на преодоление гидравлических сопротивлений. Сопротивления бывают двух типов: );
); ).
).
 – удельная потенциальная энергия положения, [Дж/кг];
– удельная потенциальная энергия положения, [Дж/кг]; – удельная потенциальная энергия давления, [Дж/кг];
– удельная потенциальная энергия давления, [Дж/кг]; – удельная кинетическая энергия;
– удельная кинетическая энергия; – удельная полная механическая энергия;
– удельная полная механическая энергия; – потери удельной механической энергии.
– потери удельной механической энергии. – статическое давление,
– статическое давление,  – динамическое давление,
– динамическое давление,  – полное гидростатическое давление.
– полное гидростатическое давление.


 – нивелирная (геометрическая) высота;
– нивелирная (геометрическая) высота; – пьезометрическая высота;
– пьезометрическая высота; – пьезометрический напор;
– пьезометрический напор;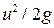 – скоростной (динамический) напор;
– скоростной (динамический) напор; – полный гидродинамический напор [м];
– полный гидродинамический напор [м]; – потери напора на участке 1-2.
– потери напора на участке 1-2.

