

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...
Топ:
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре...
Интересное:
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Для всех проектов
· 2. Оглавление. В нём приводятся все заголовки пояснительной записки и указываются страницы, на которых они находятся. Сокращать их или давать в другой формулировке, последовательности и соподчиненности нельзя. Все заголовки пишутся с прописной буквы и без точки в конце. Последнее слово каждого заголовка соединяют отточием с соответствующим ему номером страницы в правом столбце оглавления.
· 3. Введение.
· •В нем обосновывается актуальность выбранной темы, цель и содержание поста вленных задач, формулируются планируемый результат и основные проблемы, рассматриваемые в проекте,
· •указываются межпредметные связи, сообщается, кому предназначен проект и в чем состоит его новизна. Во введении также дается характеристика основных источников получения информации (официальных, научных, литературных, библиографических).
· •Желательно перечислить используемые в ходе выполнения проекта оборудование и материалы. Актуальность — обязательное требование к любой проектной работе. Обоснование ее включает оценку значимости проекта и предполагаемых результатов, раскрываются возможности их использования на практике.
· •От формулировки цели проекта необходимо перейти к указанию конкретных задач, которые предстоит решать в соответствии с ней. Это обычно делается в форме перечисления (изучить..., описать..., установить, выявить и т.п.)
Эпиграф (не обязатльно)
Мудрые мысли:
«Величие человека - в его способности мыслить».
Б. Паскаль.
«Математика- это язык, на котором говорят все точные науки».
Н.И. Лобачевский.
«Знание – столь драгоценная вещь, что его не зазорно добывать из любого источника»
|
|
Абуль-Фарадж Аль-Исфахани
· 5. Основная часть
· Главы основной части.
· • Теоретическая
· В первой главе проекта (начало исследования) рассматривается предполагаемая методика и техника его выполнения, приводится краткий обзор литературы и других материалов по теме (исторические сведения, современное состояние и др.).
· В следующей главе (поисковой) необходимо разработать банк идей и предложений по решению проблемы, рассматриваемой в проекте. Важно дать объективную оценку каждому из предлагаемых вариантов, при этом можно воспользоваться рядом определенных критериев.
· • Практическая часть проекта
· В ней необходимо разработать последовательность выполнения объекта. Она может включать в себя перечень этапов, технологическую карту, в которой описывается алгоритм операций с указанием инструментов, материалов и способов.
· Содержание глав основной части должно точно соответствовать теме работы и полностью ее раскрывать. Эти главы должны показать умение сжато, логично и аргументировано излагать материал. Не злоупотреблять перепечаткой или копированием информации из различных источников. Обязательно делать выводы о том, как эта информация пригодилась в работе.
· 6. Заключение
· Краткие выводы по результатам выполненного проекта, оценку полноты решения поставленных задач. В заключении последовательно излагаются полученные результаты, определяется их соотношение с общей целью и конкретными задачами, сформулированными во введении, дается самооценка проделанной работе. В некоторых случаях возникает необходимость указать пути продолжения исследования темы, а также конкретные задачи, которые предстоит при этом решать.
· 7. Библиографический список использованной литературы
· После заключения принято помещать список литературы, использованной при выполнении проекта. Каждый включенный в него источник должен иметь отражение в пояснительной записке. Все заимствования должны обязательно иметь подстрочные ссылки, откуда взяты приведенные материалы. Не следует включать в данный список работы, которые фактически не были использованы.
|
|
· 8. Приложения
· Вспомогательные или дополнительные материалы, которые загромождают основную часть работы, помещают в приложениях. По содержанию и форме приложения очень разнообразны. Они могут представлять собой текст, таблицы, карты, графики, рисунки. Каждое приложение должно начинаться с нового листа (страницы) с указанием в правом верхнем углу слова «Приложение» и иметь тематический заголовок. При наличии в работе более одного приложения они нумеруются арабскими цифрами (без знака №) и т. д. нумерация страниц, на которых даются приложения, должна быть сквозной и продолжать общую нумерацию основного текста. Связь его с приложениями осуществляется через ссылки, которые употребляются со словом «смотри» (см.), заключаемым вместе с шифром в круглые скобки.
Методы решения тригонометрических уравнений
· проанализировать задания ЕГЭ,
· найти информацию из ресурсов интернет. Относящиеся к теме проекта,
· выполнить практическую работу по данной теме, составив сборник заданий,
· подготовить показ конечного продукта своей работы в форме презентации, продемонстрировав глубину практической работы в рамках проекта «Методы решения тригонометрических уравнений», сделать памятку для своих сверстников.
Основополагающим вопросом, направляющий проект - вопрос «Для чего нужна тригонометрия?
-Как тригонометрия помогает решать алгебраические задачи?
- Как тригонометрия помогает решать геометрические задачи?
- Как тригонометрия помогает решать физические задачи?
-Как возникла тригонометрия?
-Какие реальные явления она описывает?
-Как применяется в физике?
-Какие методы решения тригонометрических уравнений бывают?
- Как тригонометрия помогает решить геометрические задачи?
-Зачем нужно знать тригонометрию?
-Каковы основные формулы тригонометрии?
· свободно ориентироваться в многообразных тригонометрических формулах;
· решать геометрические задачи с помощью тригонометрии;
· применять полученные знания на практике;
· выдвигать гипотезы;
· быстро и точно подбирать необходимые для работы ресурсы, вести поиск в Интернете;
|
|
· работать в различных поисковых системах;
· точно формулировать вопрос;
· представлять результаты исследований в виде презентаций, публикаций и рефератов;
· интерпретировать результаты исследования;
· делать выводы;
· обсуждать результаты исследования, участвовать в дискуссии.
саморазвитие в процессе подготовки к ЕГЭ
имеем представление о том, что подготовка к ЕГЭ – это не только изучение предмета. Умение решать складывается не только из выполнения действий по образцу, но и предполагает, что ты свободно ориентируешься в материале предмета.
несмотря на все трудности, успех на ЕГЭ возможен!
Актуальность темы:
Почему я выбрал тему ….
встречаются в курсе алгебры и начала анализа, в разделе ЕГЭ по математике
– это одна из сложнейших тем математики, которая выходит на Единый Государственный Экзамен. Очень многие учащиеся затрудняются или вообще не умеют решать …
Немаловажно знать, тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалеких звезд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Следует отметить применение тригонометрии в следующих областях: техника навигации, теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ), компьютерная томография, фармацевтика, химия, теория чисел, сейсмология, метеорология, океанология, картография, многие разделы физики, топография, геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.
Каждого изучающего математику, интересует как и где применяются полученные знания. Ответ на этот вопрос и дает данная работа.
Проблема:
Цель исследования:
|
|
Задачи:
Предмет исследования:
· ресурсы Интернет – сайтов, содержащих …
· материалы энциклопедий и справочников
· задания из Демо - вариантов ЕГЭ разных лет по математике
· способы решения …
Методы и приемы:
Гипотеза (не обязательно): Существует две гипотезы:
Выводы: Выполняя исследовательскую работу
Из истории происхождения
Слово тригонометрия составилось из двух греческих слов: τρίγονον (тригонон-треугольник) и и μετρειν (метрейн - измерять) в буквальном переводе означает измерение треугольников.
Именно эта задача- измерение треугольников или, как принято теперь говорить, решение треугольников, т.е. определение всех сторон и углов треугольника по трем его известным элементам (стороне и двум углам, двум сторонам и углу или трем сторонам)- с древнейших времен составляла основу практических приложений тригонометрии.
Как и всякая другая наука, тригонометрия выросла из человеческой практики, в процессе решения конкретных практических задач. Первые этапы развития тригонометрии тесно связаны с развитием астрономии. Большое влияние на развитие астрономии и тесно связанной с ней тригонометрии оказали потребности развивающегося мореплавания, для которого требовалось умение правильно определять курс корабля в открытом море по положению небесных светил. Значительную роль в развитии тригонометрии сыграла потребность в составлении географических карт и тесно связанная с этим необходимость правильного определения больших расстояний на земной поверхности.
|
|
Основополагающее значение для развития тригонометрии в эпоху ее зарождения имели работы древнегреческого астронома Гиппарха (середина II века до н.э.). Тригонометрия как наука, в современном смысле этого слова не было не только у Гиппарха, но и у других ученых древности, так как они еще не имели понятия о функциях углов и даже не ставили в общем виде вопроса о зависимости между углами и сторонами треугольника. Но по существу они, пользуясь известными им средствами элементарной геометрии, решали те задачи, которыми занимается тригонометрия. При этом основным средством получения нужных результатов было умение вычислять длины круговых хорд на основании известных соотношений между сторонами правильных трех-, четырех-, пяти- и десятиугольника и радиусом описанного круга.
Гиппарх составил первые таблицы хорд, т.е. таблицы, выражающие длину хорды для различных центральных углов в круге постоянного радиуса. Это были, по существу, таблицы двойных синусов половины центрального угла. Впрочем, оригинальные таблицы Гиппарха (как и почти все им написанное) до нас не дошли, и мы можем составить себе о них представление главным образом по сочинению «Великое построение» или (в арабском переводе) «Альмагест» знаменитого астронома Клавдия Птолемея, жившего в середине II века н.э.
Птолемей делил окружность на 360 градусов, а диаметр- на 120 частей. Он считал радиус равным 60 частям(60′′). Каждую из частей он делил на 60′, каждую минуту на 60′′, секунду на 60 терций (60′′′) и т.д., применяя указанное деление, Птолемей выражал сторону правильного вписанного шестиугольника или хорду, стягивающую дугу в 60° в виде 60 частей радиуса (60ч), а сторону вписанного квадрата или хорду в 90° приравнивал числу 84ч51′10″.Хорду в 120°- сторону вписанного равностороннего треугольника- он выражал числом 103ч55′23″ и т.д. Для прямоугольного треугольника с гипотенузой, равной диаметру круга, он записывал на основании теоремы Пифагора: (хорда á)2+(хорда|180-á|)2=(диаметру)2, что соответствует современной формуле sin2á+cos2á=1.
«Альмагест» содержит таблицу хорд через полградуса от 0° до 180°, которая с нашей современной точки зрения представляет таблицу синусов для углов от 0° до 90° через каждые четверть градуса.
В основе всех тригонометрических вычислений у греков лежала известная еще Гиппарху теорема Птолемея: «прямоугольник, построенный на диагоналях вписанного в круг четырехугольника, равен сумме прямоугольников, построенных на противолежащих сторонах» (произведение диагоналей равно сумме произведений противоположных сторон). Пользуясь этой теоремой, греки умели (с помощью теоремы Пифагора) по хордам двух углов вычислить хорду суммы (или хорду разности) этих углов или хорду половины данного угла, т.е. умели получать результаты, которые мы получаем теперь по формулам синуса суммы (или разности) двух углов или половины угла.
Новые шаги в развитии тригонометрии связаны с развитием математической культуры народов Индии, Средней Азии и Европы (V-XII).
Важный шаг вперед в период с V по XII век был сделан индусами, которые в отличие от греков стали рассматривать и употреблять в вычислениях уже не целую хорду ММ′ (см. чертеж) соответствующего центрального угла, а только ее половину МР, т. е. то, что мы теперь называем линией синуса á- половины центрального угла.
Наряду с синусом индусы ввели в тригонометрию косинус, точнее говоря, стали употреблять в своих вычислениях линию косинуса. (термин косинус появился значительно позднее в работах европейских ученых впервые в конце XVI в.из так называемого «синуса дополнения», т.е. синуса угла, дополняющего данный угол до 90°. «Синус дополнения» или (по латыни) sinus complementi стали сокращенно записывать как sinus co или co-sinus).
Им были известны также соотношения cosá=sin(90°-á) и sin2á+cos2á=r2, а также формулы для синуса суммы и разности двух углов.
Следующий этап в развитии тригонометрии связан со странами
Модель биоритмов
Модель биоритмов можно построить с помощью тригонометрических функций. Для построения модели биоритмов необходимо ввести дату рождения человека, дату отсчета (день, месяц, год) и длительность прогноза (кол-во дней).
Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения. При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.
Формула сердца
В результате исследования, проведенного студентом иранского университета Шираз Вахидом-Резой Аббаси, медики впервые получили возможность упорядочить информацию, относящуюся к электрической активности сердца или, другими словами, электрокардиографии.
Формула, получившая название тегеранской, была представлена широкой научной общественности на 14-й конференции географической медицины и затем - на 28-й конференции по вопросам применения компьютерной техники в кардиологии, состоявшейся в Нидерландах. Эта формула представляет собой комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии. Как утверждают медики, эта формула в значительной степени облегчает процесс описания основных параметров деятельности сердца, ускоряя, тем самым, постановку диагноза и начало собственно лечения.
Объект изучения
Введение
Тригонометрические уравнения возникают при решении задач по планиметрии, стереометрии, астрономии, физики и в других областях. Еще древнегреческие математики, используя элементы тригонометрии для решения прямоугольных треугольников, фактически составляли и решали простейшие тригонометрические уравнения. Исторически учение о решении тригонометрических уравнений формировалось с развитием теории тригонометрических функций, а также черпало из алгебры общие методы их решения.
Цель работы: изучить методы решения тригонометрических уравнений, исследовать применение их к решению уравнений повышенной сложности и задач различного содержания.
Теоретическая часть
· определение тригонометрического уравнения
· Простейшие тригонометрические уравнения
· определения arcsin a arcos a arcctq a arcctq a
· 2 основных способа решения простейших тригонометрических уравнения (1. с помощью круга 2. с помощью формул)
Поскольку каждому значению тригонометрической функции соответствует неограниченное множество углов, то тригонометрическое уравнение, если не сделано каких-либо оговорок, имеет бесчисленное множество решений.
Особо используются частные случаи элементарных тригонометрических уравнений, когда тригонометрические функции равны -1, 0, 1, в которых решение записывается без применения общих формул.
Частные случаи
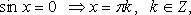
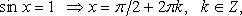
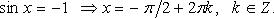
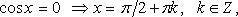
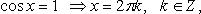
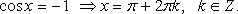
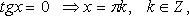
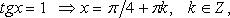
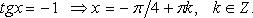
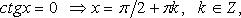
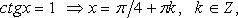
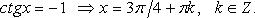
При решении тригонометрических уравнений важную роль играет период тригонометрических функций.
Рекомендации по решению тригонометрических уравнений
1. Если аргументы функций одинаковые, попробовать получить одинаковые функции, использовав формулы без изменения аргументов.
2. Если аргументы функций отличаются в два раза, попробовать получить одинаковые аргументы, использовав формулы двойного аргумента.
3. Если аргументы функций отличаются в четыре раза, попробовать их привести к промежуточному двойному аргументу.
4. Если есть функции одного аргумента, степени свыше первой, попробовать понизить степень, используя формулы понижения степени или формулы сокращенного умножения.
5. Если есть сумма одноименных функций первой степени с разными аргументами (вне случаев 2,3), попробовать преобразовать сумму в произведение для появления общего множителя.
6. Если есть сумма разноимённых функций первой степени с разными аргументами (вне случаев 2, 3), попробовать использовать формулы приведения, получить затем случай 5.
7. Если в уравнении есть произведение косинусов (синусов) различных аргументов, попробовать свести его к формуле синус двойного аргумента, умножив и разделив это выражение на синус (косинус) подходящего аргумента:
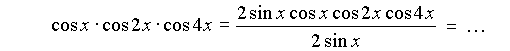
8. Если в уравнении есть числовое слагаемое (множитель), то его можно представить в виде значений функции угла. Например:
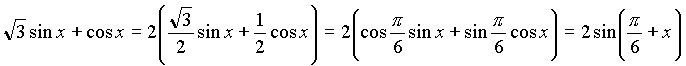
Практическая часть
Примеры
1) Решить уравнение 2sin2 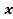 + 3sin
+ 3sin 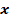 —2 = 0.
—2 = 0.
Это уравнение является квадратным относительно sin 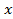 .
.
Его корни: sin 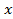 =
=  , sin
, sin 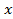 =—2. Второе из полученных простейших уравнений не имеет решений, так как Isin
=—2. Второе из полученных простейших уравнений не имеет решений, так как Isin 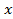 l
l 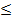 1, решения первого можно записать так:
1, решения первого можно записать так:
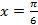 +2k
+2k 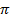 ,
, 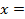 π
π 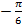 + 2k
+ 2k 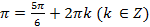
Если в уравнении встречаются разные тригонометрические функции, то надо заменить их все на какую-нибудь одну, используя тригонометрические тождества.
2) Решить уравнение 2sin 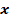 + cos
+ cos 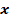 = 2.
= 2.
Если в этом уравнении заменим косинус на синус (по аналогии с предыдущими примерами) или наоборот, то получим уравнение с радикалами. Чтобы избежать этого, используем формулы, выражающие синус и косинус через тангенс половинного угла:
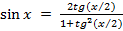 и
и 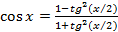 .
.
Делая замену, получаем уравнение относительно 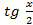 :
: 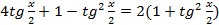 .
.
Квадратное уравнение 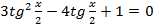 имеет корни
имеет корни 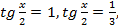 откуда
откуда
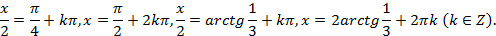
Это же уравнение можно решить другим способом, вводя вспомогательный угол:
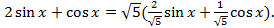
Пусть 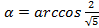 . Тогда можно продолжить преобразование:
. Тогда можно продолжить преобразование: 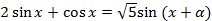 . Получаем простейшее уравнение
. Получаем простейшее уравнение 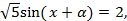 т. е.
т. е. 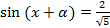 , откуда
, откуда 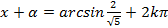 , или
, или 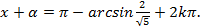
Ответ получился в другом виде, однако можно проверить, что решения на самом деле совпадают.
2. Понижение порядка уравнения.
Формулы удвоения 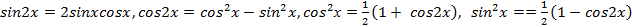 позволяют квадраты синуса, косинуса и их произведения заменять линейными функциями от синуса и косинуса двойного угла. Такие замены делать выгодно, так как они понижают порядок уравнения.
позволяют квадраты синуса, косинуса и их произведения заменять линейными функциями от синуса и косинуса двойного угла. Такие замены делать выгодно, так как они понижают порядок уравнения.
Примеры
1) Решить уравнение 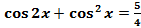 .
.
Можно заменить cos2 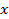 на 2cos2
на 2cos2 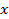 —1 и получить квадратное уравнение относительно cos
—1 и получить квадратное уравнение относительно cos 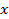 , но проще заменить
, но проще заменить 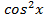 на
на 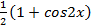 и получить линейное уравнение относительно
и получить линейное уравнение относительно 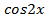 .
.
2) Решить уравнение 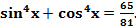
Подставляя вместо 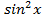 ,
, 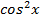 их выражения через
их выражения через 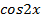 , получаем:
, получаем:
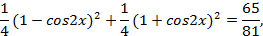
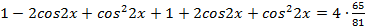 ,
,
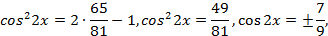
2 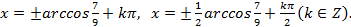
3. Использование тригонометрических формул сложения и следствий из них.
Иногда в уравнениях встречаются тригонометрические функции кратных углов. В таких случаях нужно использовать формулы сложения.
Примеры
1) Решить уравнение 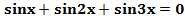 .
.
Сложим два крайних слагаемых: 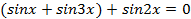 , откуда
, откуда 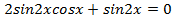 ,
, 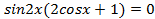 . Тогда
. Тогда 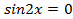 ,
, 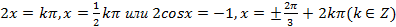 .
.
2) Решить уравнение 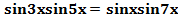 .
.
Преобразуем произведение синусов в сумму: 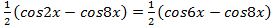 ,
,
откуда 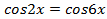 . Полученное уравнение можно решить разными способами: 1) воспользоваться формулами сложения; 2) преобразовать
. Полученное уравнение можно решить разными способами: 1) воспользоваться формулами сложения; 2) преобразовать 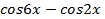 в произведение. Удобнее воспользоваться условием равенства косинусов двух углов
в произведение. Удобнее воспользоваться условием равенства косинусов двух углов 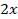 и
и 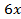 :
: 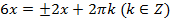 .
.
Получаем два уравнения: 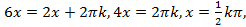
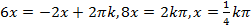 .
.
Здесь решения второй серии содержат в себе все решения первой серии. Учитывая это, ответ можно записать короче: 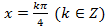 .
.
4. Однородные уравнения.
Уравнение, в котором каждое слагаемое имеет одну и ту же степень, называется однородным. Его можно решить, выполнив деление на старшую степень синуса (или косинуса).
Так как 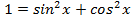 , то постоянные слагаемые можно считать членами второй степени.
, то постоянные слагаемые можно считать членами второй степени.
Пример: 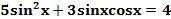 .
.
Заменяя 4 на 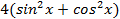 ,получаем:
,получаем: 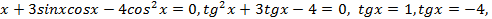
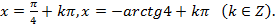
5. Переход к половинному углу
Рассмотрим этот метод на примере:
Пример 6. Решить уравнение: 3 sin x – 5 cos x = 7.
Решение.
6 sin (x / 2) · cos (x / 2) – 5 cos ² (x / 2) + 5 sin ² (x / 2) =
= 7 sin ² (x / 2) + 7 cos ² (x / 2),
2 sin ² (x / 2) – 6 sin (x / 2) · cos (x / 2) + 12 cos ² (x / 2) = 0,
tg ² (x / 2) – 3 tg (x / 2) + 6 = 0,
6. Введение вспомогательного угла
Рассмотрим уравнение вида:
a sin x + b cos x = c,
где a, b, c – коэффициенты; x – неизвестное.
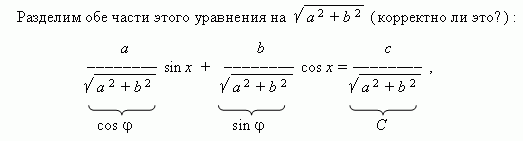
Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль (абсолютное значение) каждого из них не больше 1, а сумма их квадратов равна 1. Тогда можно обозначить их соответственно как cos 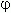 и sin
и sin 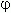 (здесь
(здесь 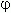 - так называемый вспомогательный угол), и наше уравнение принимает вид:
- так называемый вспомогательный угол), и наше уравнение принимает вид:
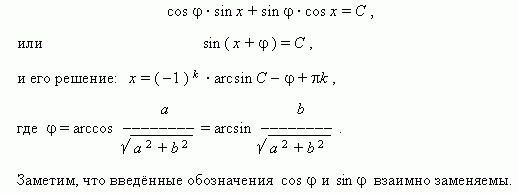
Пример. Решить уравнение: 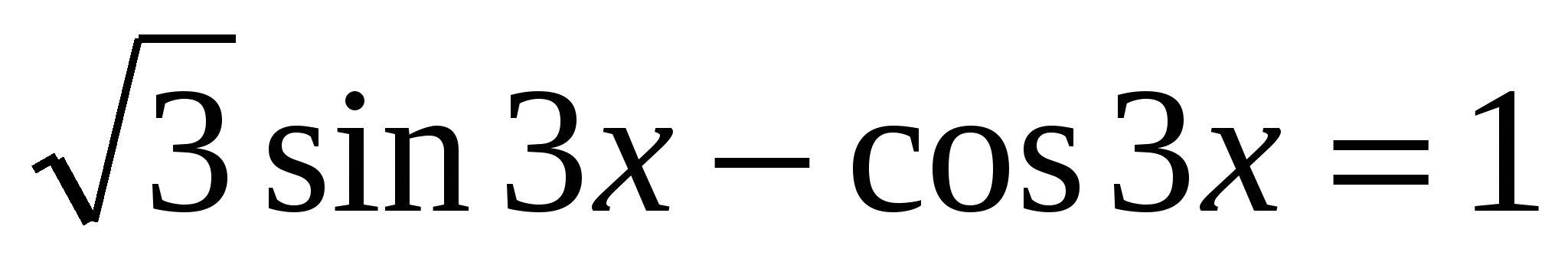
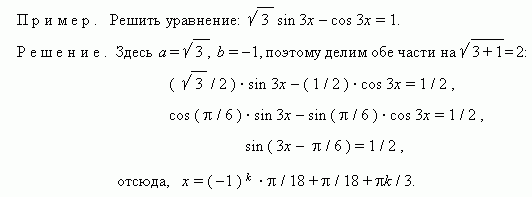
Приемы решения тригонометрических уравнений, требующих искусственных преобразований.
1. Умножение обеих частей уравнения на одну и ту же тригонометрическую функцию.
Пример. Решите уравнение 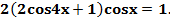
Решение. Раскроем скобки и преобразуем произведение
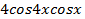 в сумму:
в сумму: 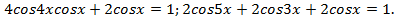
Умножим обе части уравнения на 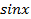 . Заметим, что
. Заметим, что 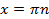 ,
,  не является решением данного уравнения.
не является решением данного уравнения. 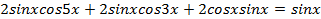 . Преобразуем левую часть уравнения:
. Преобразуем левую часть уравнения:
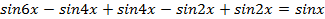 ;
; 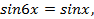 или
или 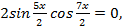 тогда
тогда
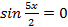 или
или 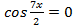 , т.е.
, т.е. 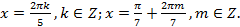
Исключим из найденных серий корни вида 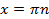 ,
,  :
:
а) 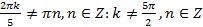 . Ясно, что
. Ясно, что 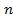 - четное число, т.е.
- четное число, т.е. 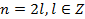 , а потому
, а потому 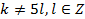 .
.
б) 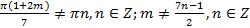 .Tax как
.Tax как 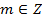 , то
, то 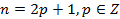 ,но тогда
,но тогда 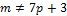 ,
, 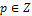 .
.
Ответ: 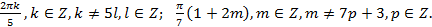
2. Прибавление к обеим частям уравнения одного и того же числа, одной и той же тригонометрической функции.
Пример. Решите уравнение 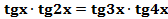 .
.
Решение. Область определения уравнения задается неравенствами:
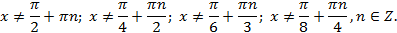
При6авим к обеим частям уравнения по единице. 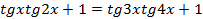 ;
;
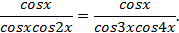
Разделим обе части уравнения на 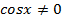 и после преобразований получим.
и после преобразований получим.
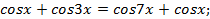
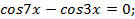
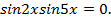
Тогда 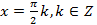 или
или 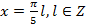 .
.
Из первой серии корней области определения принадлежит только  ,
, 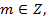 но это серия корней содержится в серии
но это серия корней содержится в серии 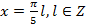 . Нетрудно убедиться, что
. Нетрудно убедиться, что 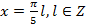 входит в область определения. Например:
входит в область определения. Например: 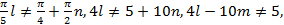 что верно, поскольку левая часть - число четное, а правая - нечетное.
что верно, поскольку левая часть - число четное, а правая - нечетное.
Ответ: 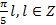 .
.
3. Тождественные преобразования одной из частей уравнения.
Пример. Решите уравнение 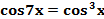 .
.
Решение. Преобразуем левую часть уравнения:
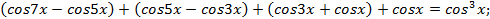
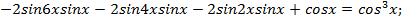
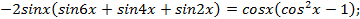
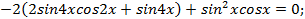
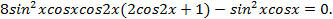
Откуда 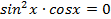 , тогда
, тогда 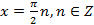 или
или 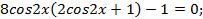
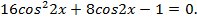
Легко видеть, что 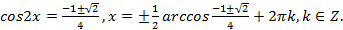
Ответ: 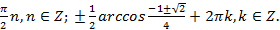
4. Использование свойств пропорции.
Необходимо помнить, что применение равенств
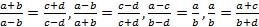 и т. д. приводит к изменению области определения уравнения. Так, у пропорции
и т. д. приводит к изменению области определения уравнения. Так, у пропорции 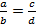 существует ограничение:
существует ограничение: 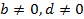 , а у пропорции
, а у пропорции 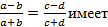 место другое ограничение:
место другое ограничение: 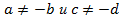 .
.
Пример. Решите уравнение 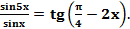
Решение. Применяя формулу тангенса разности, получим уравнение: 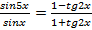 . Используем свойство пропорции:
. Используем свойство пропорции: 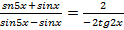 ;
; 
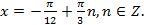 Область определения исходного уравнения:
Область определения исходного уравнения: 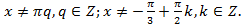
В ходе решения произошло сужение области определения, добавились новые, ограничения: 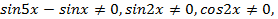 откуда
откуда 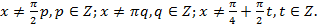
Проверим, удовлетворяют ли исходному уравнению значения
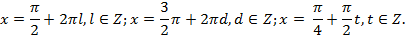
а) 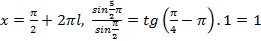 -верное равенство,
-верное равенство,
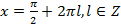 - решение исходного уравнения.
- решение исходного уравнения.
б) 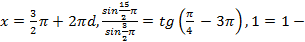 верное равенство.
верное равенство.
в) 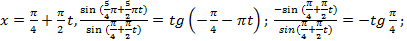 -1
-1 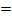 -1 - верное равенство, Ответ:
-1 - верное равенство, Ответ: 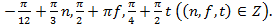
5. Решение тригонометрических уравнений методом экстремальных значений.
При решении некоторых тригонометрических уравнений бывает удобно использовать ограниченность функций, 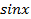 и
и 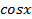 . Покажем это на конкретных примерах.
. Покажем это на конкретных примерах.
Пример 1. Решите уравнение 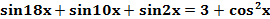 .
.
Решение. Так как 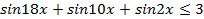 , то
, то 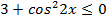 ,
, 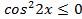 , откуда
, откуда 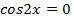 и возможные корни данного уравнения
и возможные корни данного уравнения 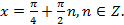 Подставив эти значения в левую часть уравнения, получим
Подставив эти значения в левую часть уравнения, получим 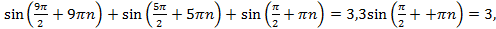 а последнее равенство возможно только при
а последнее равенство возможно только при 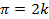 .
.
Следовательно,

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!