1.Функция распределения Гаусса
Пусть мы проводим серию измерений одной и той же величины. Из-за наличия случайных ошибок отдельные значения x 1, x 2 и т.д. будут неодинаковы. В качестве наилучшего значения измеряемой величины выбирается среднее арифметическое  . Но это не означает, что величина
. Но это не означает, что величина  равна истинному значению, которое обозначим Х. Мы можем предположить, что имеется вероятность того, что Х лежит в каких-то пределах вблизи
равна истинному значению, которое обозначим Х. Мы можем предположить, что имеется вероятность того, что Х лежит в каких-то пределах вблизи  . Интуитивно понятно, что чем больше разброс результатов измерений, тем больше ошибка в величине
. Интуитивно понятно, что чем больше разброс результатов измерений, тем больше ошибка в величине  .
.
Результаты серии измерений одной величины можно наглядно представить, построив диаграмму, которая показывает, как часто получалось то или иное значение. Такая диаграмма называется гистограммой (рис. П1). Для этого мы разбиваем весь диапазон измеряемых значений на равные интервалы и подсчитываем, сколько раз измеренная величина попадает в каждый интервал.


Рис. П1 
Теперь представим, что число измеренных значений очень велико, а ширина интервалов очень мала. Тогда вместо гистограммы можно построить график, который бы давал долю полного числа отсчетов N, попадающих в каждый интервал. Полученная гладкая кривая называется функцией плотности вероятности  (Probability Density Function − PDF). Её смысл состоит в том, что произведение
(Probability Density Function − PDF). Её смысл состоит в том, что произведение 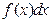 дает долю полного числа отсчетов N, приходящихся на интервал от x до
дает долю полного числа отсчетов N, приходящихся на интервал от x до  . То есть произведение
. То есть произведение  есть вероятность того, что отдельное случайно выбранное значение измеряемой величины окажется в интервале от x до
есть вероятность того, что отдельное случайно выбранное значение измеряемой величины окажется в интервале от x до  . Примерный вид такой функции
. Примерный вид такой функции  показан на рис. П1.
показан на рис. П1.
По определению функция  удовлетворяет условию
удовлетворяет условию
 . (П1)
. (П1)
Тогда среднее значение (то есть среднее арифметическое значение) для данного распределения будет равно
 (П2)
(П2)
Если число измерений велико, а систематические ошибки отсутствуют, мы будем полагать, что  совпадает с истинным значением Х.
совпадает с истинным значением Х.
Ошибка в измеренном значении x равна:
 .
.
Квадратный корень из среднего квадрата разности 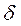 обозначается через
обозначается через  и называетсясреднеквадратическим (стандартным) отклонением, а величина
и называетсясреднеквадратическим (стандартным) отклонением, а величина  называется дисперсией:
называется дисперсией:
 . (П3)
. (П3)
Дисперсия служит мерой ширины функции распределения, то есть разброса результатов измерений. При точных измерениях кривая распределения имеет узкий максимум вблизи значения  , и величина
, и величина  будет мала.
будет мала.
Помимо среднеквадратического отклонения в качестве характеристики ширины распределения можно пользоваться и другой величиной, которая называется средним отклонением или средней ошибкой:
 . (П4)
. (П4)
Модуль от величины  взят потому, что в противном случае из-за наличия у этой разности обоих знаков интеграл был бы равен нулю.
взят потому, что в противном случае из-за наличия у этой разности обоих знаков интеграл был бы равен нулю.
Однако необходимо знать точный вид функции распределения. Согласно центральной предельной теореме теории случайных процессов любые физические явления, возникающие в результате воздействия суммы большого числа независимых случайных событий, подчиняются нормальному распределению плотности вероятности случайной величины, т.е. являются гауссовским случайным процессом (рис. П2):
 (П5)
(П5)
Во многих случаях полагают Х = 0. Легко убедиться, что распределение Гаусса удовлетворяет условию (П1). В точках 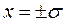 функция имеет точки перегиба. На рис. П2 представлено несколько гауссовых распределений с разными
функция имеет точки перегиба. На рис. П2 представлено несколько гауссовых распределений с разными  .
.
В некоторых случаях необходимо знать, какая доля F (x) измеренных значений приходится на интервал от - х до х. По определению величина f (x) – это доля показаний, приходящихся на интервал от - х до х. Поэтому
 (П6)
(П6)

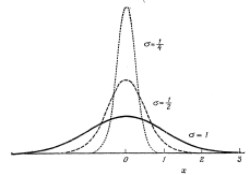

Рис.П2
Функция F (x) (рис. П2) зависит от  . Легко показать, используя функцию распределения Гаусса, что в пределах
. Легко показать, используя функцию распределения Гаусса, что в пределах  заключено примерно две трети результатов (рис. П3). Вне интервала
заключено примерно две трети результатов (рис. П3). Вне интервала  остается одна двадцатая часть результатов, а вне интервала
остается одна двадцатая часть результатов, а вне интервала  − лишь одна четырехсотая.
− лишь одна четырехсотая.

Рис. П3.
Явления, в которых в силу случайного процесса измеряемые величины изменяются дискретно (например, при регистрации числа частиц в ядерной физике), описываются распределением Пуассона.
Распределение Пуассона
Распределение Пуассона возникает при выполнении следующих условий:
1. Случайная величина (число отсчетов) может принимать только целые положительные значения, включая 0.
2. Распределение Пуассона описывает редкие события – вероятность двух (и более) событий на достаточно малом временном или пространственном интервале бесконечно мала по сравнению с вероятностью одного события.
3. События должны быть статистически независимыми (во времени или пространстве).
4. Поток событий считается стационарным, т. е. не зависящим от начала отсчета временной или пространственной координаты.
Распределение Пуассона имеет вид
 , (П7)
, (П7)
где  −вероятность того, что за время t произойдет k событий,
−вероятность того, что за время t произойдет k событий,  − интенсивность появления ожидаемого события, под которым понимается среднее число событий в единицу времени, t − время с начала отсчета.
− интенсивность появления ожидаемого события, под которым понимается среднее число событий в единицу времени, t − время с начала отсчета.
Определим среднее число событий  за время t. Оно определяется равенством
за время t. Оно определяется равенством
 . (П8)
. (П8)
Тогда
 . (П9)
. (П9)
Таким образом, можно записать
 , (П10)
, (П10)
где  .
.
Как видно из (П10), распределение Пуассона полностью определяется заданием только одного параметра − среднего числа событий 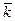 .
.
Заметим, что закон Пуассона в форме (П10) не содержит в явном виде информацию о том, какое именно распределение (временнóе или пространственное) изучается. Число  может быть средним числом событий за время t, тогда
может быть средним числом событий за время t, тогда 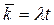 . Но k может быть и средним числом событий в данном элементе пространства, тогда
. Но k может быть и средним числом событий в данном элементе пространства, тогда 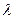 будет иметь смысл пространственной интенсивности – числа событий на интервале х.
будет иметь смысл пространственной интенсивности – числа событий на интервале х.
Также отметим, что любое статистическое распределение должно быть нормировано согласно требованию, чтобы вероятность достоверного события равнялась единице. В нашем случае условие нормировки выполняется:

 . (П11)
. (П11)
Важнейшими характеристиками статистического распределения являются среднее значение и дисперсия. Среднее значение  определяет положение распределения на оси абсцисс, а дисперсия
определяет положение распределения на оси абсцисс, а дисперсия 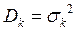 − разброс случайных значений относительно этого среднего. Для дискретных законов распределения среднее значение и дисперсия случайной величины k определяются соответственно:
− разброс случайных значений относительно этого среднего. Для дискретных законов распределения среднее значение и дисперсия случайной величины k определяются соответственно:
 (П12)
(П12)
 (П13)
(П13)
Если использовать распределение Пуассона (П10), то из (П13) получается
 . (П14)
. (П14)
Такая связь между дисперсией и средним значением случайной величины характерна только для пуассоновского распределения и является его отличительным признаком.
Среднеквадратическое (стандартное) отклонение (ошибка) 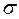 связано с дисперсией соотношением
связано с дисперсией соотношением
 . (П15)
. (П15)
Из выражений (П14) и (П15) следует, что относительная статистическая ошибка измерения случайной величины k, распределенной по закону Пуассона, равна
 . (П16)
. (П16)
Рассмотрим несколько важных примеров использования распределения Пуассона.
Пример 1. Средняя длина пробега электронов в канале МДП транзистора равна  . Найти вероятность того, что электрон пролетит расстояние х без столкновений.
. Найти вероятность того, что электрон пролетит расстояние х без столкновений.
Решение. Интенсивность процесса составляет  − среднее число столкновений на единице пути. Тогда
− среднее число столкновений на единице пути. Тогда  − среднее число столкновений на интервале х. Вероятность того, что электрон пролетит путь длиной х без столкновений (то есть
− среднее число столкновений на интервале х. Вероятность того, что электрон пролетит путь длиной х без столкновений (то есть  ) в соответствии с формулой (П7) составляет
) в соответствии с формулой (П7) составляет
 . (П17)
. (П17)
На длине  в электрическом поле электрон набирает энергию
в электрическом поле электрон набирает энергию  , на длине х − энергию
, на длине х − энергию  . Таким образом, вероятность того, что электрон на пути х наберет энергию, равную энергии ионизации
. Таким образом, вероятность того, что электрон на пути х наберет энергию, равную энергии ионизации  , равна
, равна
 . (П18)
. (П18)
Эту вероятность можно рассматривать также как долю электронов, избежавших столкновения до набора энергии  .
.
Пример 2. Рассчитать статистически случайную флуктуацию числа атомов примеси внутри данного объема v около их среднего значения, если полупроводник легирован однородно с концентрацией примеси (для определенности акцепторной) N а.
Решение. Среднее число атомов примеси в объеме v составляет N а v. Вероятность того, что в этом объеме будет N 0 атомов равна
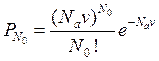 .
.
Согласно (П15) среднеквадратическое (стандартное) отклонение (флуктуация) составляет
 , (П19)
, (П19)
а отношение флуктуации к среднему значению составляет
 . (П20)
. (П20)



 . Но это не означает, что величина
. Но это не означает, что величина  равна истинному значению, которое обозначим Х. Мы можем предположить, что имеется вероятность того, что Х лежит в каких-то пределах вблизи
равна истинному значению, которое обозначим Х. Мы можем предположить, что имеется вероятность того, что Х лежит в каких-то пределах вблизи  .
.


 (Probability Density Function − PDF). Её смысл состоит в том, что произведение
(Probability Density Function − PDF). Её смысл состоит в том, что произведение 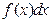 дает долю полного числа отсчетов N, приходящихся на интервал от x до
дает долю полного числа отсчетов N, приходящихся на интервал от x до  . То есть произведение
. То есть произведение  есть вероятность того, что отдельное случайно выбранное значение измеряемой величины окажется в интервале от x до
есть вероятность того, что отдельное случайно выбранное значение измеряемой величины окажется в интервале от x до  . Примерный вид такой функции
. Примерный вид такой функции  показан на рис. П1.
показан на рис. П1. . (П1)
. (П1) (П2)
(П2) совпадает с истинным значением Х.
совпадает с истинным значением Х. .
.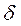 обозначается через
обозначается через  и называетсясреднеквадратическим (стандартным) отклонением, а величина
и называетсясреднеквадратическим (стандартным) отклонением, а величина  называется дисперсией:
называется дисперсией: . (П3)
. (П3) , и величина
, и величина  будет мала.
будет мала. . (П4)
. (П4) взят потому, что в противном случае из-за наличия у этой разности обоих знаков интеграл был бы равен нулю.
взят потому, что в противном случае из-за наличия у этой разности обоих знаков интеграл был бы равен нулю. (П5)
(П5)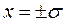 функция имеет точки перегиба. На рис. П2 представлено несколько гауссовых распределений с разными
функция имеет точки перегиба. На рис. П2 представлено несколько гауссовых распределений с разными  .
. (П6)
(П6)


 заключено примерно две трети результатов (рис. П3). Вне интервала
заключено примерно две трети результатов (рис. П3). Вне интервала  остается одна двадцатая часть результатов, а вне интервала
остается одна двадцатая часть результатов, а вне интервала  − лишь одна четырехсотая.
− лишь одна четырехсотая.
 , (П7)
, (П7) −вероятность того, что за время t произойдет k событий,
−вероятность того, что за время t произойдет k событий,  − интенсивность появления ожидаемого события, под которым понимается среднее число событий в единицу времени, t − время с начала отсчета.
− интенсивность появления ожидаемого события, под которым понимается среднее число событий в единицу времени, t − время с начала отсчета. за время t. Оно определяется равенством
за время t. Оно определяется равенством . (П8)
. (П8) . (П9)
. (П9) , (П10)
, (П10) .
.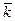 .
.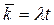 . Но k может быть и средним числом событий в данном элементе пространства, тогда
. Но k может быть и средним числом событий в данном элементе пространства, тогда 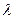 будет иметь смысл пространственной интенсивности – числа событий на интервале х.
будет иметь смысл пространственной интенсивности – числа событий на интервале х. . (П11)
. (П11) определяет положение распределения на оси абсцисс, а дисперсия
определяет положение распределения на оси абсцисс, а дисперсия 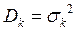 − разброс случайных значений относительно этого среднего. Для дискретных законов распределения среднее значение и дисперсия случайной величины k определяются соответственно:
− разброс случайных значений относительно этого среднего. Для дискретных законов распределения среднее значение и дисперсия случайной величины k определяются соответственно: (П12)
(П12) (П13)
(П13) . (П14)
. (П14)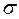 связано с дисперсией соотношением
связано с дисперсией соотношением . (П15)
. (П15) . (П16)
. (П16) . Найти вероятность того, что электрон пролетит расстояние х без столкновений.
. Найти вероятность того, что электрон пролетит расстояние х без столкновений. − среднее число столкновений на единице пути. Тогда
− среднее число столкновений на единице пути. Тогда  − среднее число столкновений на интервале х. Вероятность того, что электрон пролетит путь длиной х без столкновений (то есть
− среднее число столкновений на интервале х. Вероятность того, что электрон пролетит путь длиной х без столкновений (то есть  ) в соответствии с формулой (П7) составляет
) в соответствии с формулой (П7) составляет . (П17)
. (П17) , на длине х − энергию
, на длине х − энергию  . Таким образом, вероятность того, что электрон на пути х наберет энергию, равную энергии ионизации
. Таким образом, вероятность того, что электрон на пути х наберет энергию, равную энергии ионизации  , равна
, равна . (П18)
. (П18) .
.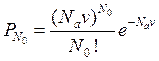 .
. , (П19)
, (П19) . (П20)
. (П20)

