Анализ сетей Петри на основе матричных уравнений

Анализ сетей

 

Сеть Петри ограничена тогда и только тогда, когда символ w отсутствует в ее дереве достижимости. Если сеть ограничена и символ w отсутствует в дереве достижимости, то сеть представляет систему конечных состояний. Это позволяет решить вопросы анализа простым перебором и проверкой конечного множества всех достижимых маркировок.

Сеть Петри является сохраняющей, если она не теряет и не порождает метки, а просто передвигает их. Свойство сохранения проверяется по дереву достижимости вычислением для каждой маркировки суммы меток. Если метки взвешены, то вычисляется взвешенная сумма. Если сумма одинакова для каждой достижимой маркировки, сеть - сохраняющая.

Задача покрываемости маркировки М маркировкой М’ сводится к поиску на дереве такой вершины х, состояние которой покрывает состояние М. Если такой вершины М(х) не существует, маркировка М не покрывается никакой достижимой маркировкой.

Таким образом, дерево достижимости можно использовать для решения задач безопасности, ограниченности, сохранения и покрываемости. К сожалению, в общем случае его нельзя использовать для решения задач достижимости и активности, а также для определения возможной последовательности запусков. Решение этих задач ограничено существованием символа w. Символ w означает потерю информации, конкретные количества меток отбрасываются, учитывается только существование их большого числа. Вместе с тем, в отдельных конкретных случаях дерево достижимости позволяет судить о свойствах достижимости и активности. Например, сеть, дерево достижимости которой содержит терминальную вершину, не активна. Аналогично искомая маркировка M’ в задаче достижимости может встретиться в дереве достижимости, что означает ее достижимость. Кроме того, если маркировка не покрывается некоторой вершиной дерева достижимости, то она недостижима.

 

 

Раскрашенные сети

 

Такие сети являются естественной интерпретацией реальных систем, аналогичной многоклассовым сетям с очередями. Однако эти многоклассовые сети не допускают представления эффектов размножения и синхронизации, отражаемых с помощью переходов в сетях Петри.

Метками раскрашенной сети приписывают атрибуты, которые называют цветами. Правила возбуждения переходов дополняются условиями, предполагающими выбор меток определённых цветов из позиций Pre(t_j). Срабатывание переходов сопровождается посылкой в позиции Post(t_j) меток, с задаваемыми значениями цвета.

 

 

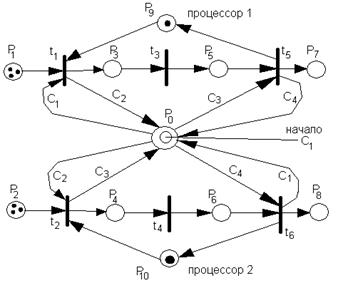
t₁, t₂ - загрузка процессоров

t₃, t₄ - обработка

t₅, t₆ - освобождение процессоров

P₀ - позиция супервизора

P₁, P₂ - заявки на обработку

P₃, P₄ - Заявки приняты

P₅, P₆ - конец обработки

P₇, P₈ - обработанные заявки

P₉, P₁₀ - двоичные семафоры, исключающие попытки запустить занятые процессоры.

На Рис.1 приведена модель процессов в двухпроцессорной системе, управляемой супервизором. Множество атрибутов-цветов, связываемых с метками и дугами сети, принято равным С = {λ, C₁, C₂, C₃, C₄}. В сети раскрашена метка, имитирующая работу супервизора и дуги, имитирующие последовательность запуска процессоров. Прочие дуги, а также метки-заявки и метки управления не нарушены.

Начальный цвет метки в P₀ равен C₁ и дуга (P₀,t­₁) окрашена в C₁. Поэтому условие возбуждения выполнимо для перехода t₁. После срабатывания t₁ в P₀ метка возвращается, уже имея цвет C₂, поскольку дуга (t₁,P₀) раскрашена в цвет C₂.

Раскрашивание дуг обеспечивает возбуждение только одного из переходов, следующих за P₀, при любом состоянии системы. При данной раскраске алгоритм работы

супервизора представлен последовательностью срабатывания переходов t₁, t₂ (t₃, t₄) t₅, t₆, т. е. происходит запуск первого процессора, затем второго, после чего следует их освобождение и цикл повторяется.

 

 

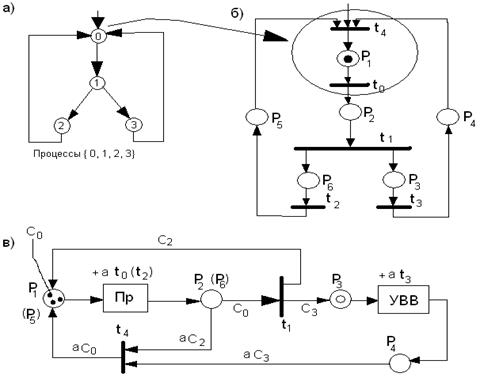
В примере 2 раскрашенная сеть используется для представления мультипрограммного выполнения алгоритма с ветвями и точкой синхронизации в ВС с процессором и УВВ.

а) – граф алгоритма

б) – биграф алгоритма

в) – модель мультипрограммного выполнения алгоритмов, представленная раскрашенной сетью.

На Пр и УВВ параллельно могут выполняться операторы 2 и 3, завершение которых является условием выполнения оператора 0 (что видно из Рис.а). Переходы t₀ – t₃ биграфа (Рис. б) соответствуют вершинам графа на (Рис. а). Для отображения точки входа в алгоритм на его биграфе введена маркированная позиция P₁, поэтому нулевой вершине графа (Рис. а) поставлены в соответствие переходы t₀ и t₄ биграфа. При построении сети (Рис. в) учтено, что время выполнения операций t₁ и t₄ мало по сравнению с остальными. Учитывая также, что действия t₀ и t₂ выполняются на процессоре, позиции P₁ и P₅, а также P₂ и P₆ биграфа совмещены на (Рис. в) и обозначены как P₁ и P₂. Процессы выполнения алгоритмов представлены движением меток. Раскраска меток двухэлементная, определяющая номер процесса a = {1, 2, 3} и номер этапа обработки C = {C₀, C₁, C₂, C₃}.

Из (Рис. в) видно, что некоторые из дуг раскрашены одним цветом (C_i), другие парой цветов (a C_i), третьи не раскрашены вовсе, что учитывается при управлении возбуждением переходов и изменении цвета меток. Заметим, что при раскрашивании парой цветов все эти признаки анализируются или изменяются в комплексе. Например, входные дуги перехода t₄ помечены парами a C₂ и a C₃, что определяет выбор для синхронизации на t₄ процессов с одним и тем же номером a и завершенными этапами обработки C₂ и C₃ соответственно.

Следующий пример 3 показывает изобразительные возможности раскрашенных сетей по разделению путей данных и управления в УВВ. Данные от двух источников U₁ и U₂ помечены квадратами в P₁ и P₃, а сигналы запроса на обработку – кружками в P₂ и P₄. Запросы принимаются (переходы t₁, t₂), накапливаются в регистре (позиция P₅), выбираются из неё (переход t₃) и запускают пересылку данных от источников (P₁ или P₃) в буфер P₇. Метка-треугольник в позиции P₈ отражает управляющий процесс, разрешающий выполнение только одной из двух операций считывания t₄ или t₅.

 

ПРИМЕР 3

 

 

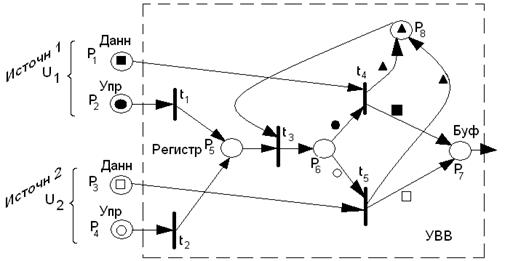
Таким образом, процедура раскраски сети Петри – это модельный способ трактовки различных по характеру реальных элементов:

- в алгоритмах – номера оператора или этапа обработки;

- в мультипрограммных системах – номера задачи, её приоритета и других атрибутов;

- для ресурсов – их типа, способы использования и т. п.

 

 

Анализ сетей

 

Сеть Петри ограничена тогда и только тогда, когда символ w отсутствует в ее дереве достижимости. Если сеть ограничена и символ w отсутствует в дереве достижимости, то сеть представляет систему конечных состояний. Это позволяет решить вопросы анализа простым перебором и проверкой конечного множества всех достижимых маркировок.

Сеть Петри является сохраняющей, если она не теряет и не порождает метки, а просто передвигает их. Свойство сохранения проверяется по дереву достижимости вычислением для каждой маркировки суммы меток. Если метки взвешены, то вычисляется взвешенная сумма. Если сумма одинакова для каждой достижимой маркировки, сеть - сохраняющая.

Задача покрываемости маркировки М маркировкой М’ сводится к поиску на дереве такой вершины х, состояние которой покрывает состояние М. Если такой вершины М(х) не существует, маркировка М не покрывается никакой достижимой маркировкой.

Таким образом, дерево достижимости можно использовать для решения задач безопасности, ограниченности, сохранения и покрываемости. К сожалению, в общем случае его нельзя использовать для решения задач достижимости и активности, а также для определения возможной последовательности запусков. Решение этих задач ограничено существованием символа w. Символ w означает потерю информации, конкретные количества меток отбрасываются, учитывается только существование их большого числа. Вместе с тем, в отдельных конкретных случаях дерево достижимости позволяет судить о свойствах достижимости и активности. Например, сеть, дерево достижимости которой содержит терминальную вершину, не активна. Аналогично искомая маркировка M’ в задаче достижимости может встретиться в дереве достижимости, что означает ее достижимость. Кроме того, если маркировка не покрывается некоторой вершиной дерева достижимости, то она недостижима.

 

 

Анализ сетей Петри на основе матричных уравнений

 

Матричный подход основывается на представлении сети двумя матрицами Д^- и Д⁺, представляющими входную и выходную функции сети. Каждая матрица имеет m строк (по одной на переход) и n столбцов (по одному на позицию). Определим                        Д^-(j,i)=K(P_i,I(t_j)), а Д⁺(j,i)=K(P_i,O(t_j)). Д^- определяет входы в переходы, Д⁺ - выходы. K – кратность позиции по входам и выходам.

Введём m - вектор e(j), содержащий нули везде, за исключением j-й компоненты. Переход t_j представляется m - вектором e(j).

Тогда переход t_j в маркировке М разрешён, если М≥e(j)Д^-, а результат запуска перехода t_j в маркировке М записывается как:

 

δ(M,t_j)=M - e(j) Д^- + e(j) Д⁺ = M+ e(j)(- Д^- + Д⁺) = M + e(j)Д

 

где Д = Д⁺ - Д^- - составная матрица изменений.

Тогда для последовательности запусков переходов G = t_j1, t_j2,…, t_jk имеем

 

δ(M,G) =δ(M, t_j1, t_j2,…, t_jk) =

= M + e(j₁)Д + e(j₂)Д + … + e(j_k)Д =

= M +[ e(j₁) + e(j₂) + … + e(j_k)]Д = M + f(G)Д    (1)

 

Вектор f(G) = e(j₁)+e(j₂) …..+e(j_k) называется вектором запуска последовательности t_j1,t_j2,…,t_jk. i-й элемент вектора f(G), f(G)_i - это число запусков перехода t_j в последовательности t_j1,t_j2,…,t_jk. Вектор запусков, следовательно, является вектором с неотрицательными целыми компонентами.

Рассмотрим задачу сохранения при известном векторе взвешивания меток W. Если M₀ - начальная маркировка, а M’ - произвольная достижимая маркировка, необходимо, чтобы M₀W = M’W. Тогда существует последовательность запусков переходов G, которая переводит сеть из M₀ в M’. Поэтому

 

M’ = δ(M₀,G) = M₀ + f(G)Д

 

Следовательно, M₀W = M’W = (M₀ + f(G) Д) W = M₀W + f(G) ДW, поэтому f(G)ДW = 0.

Поскольку это должно быть верно для всех f(G), имеем ДW = 0.

Таким образом, сеть Петри является сохраняющей тогда и только тогда, когда существует такой положительный вектор W, что ДW = 0. Это обеспечивает простой алгоритм проверки сохранения, а также позволяет получать вектор взвешивания W для сохраняющей сети.

Матричная теория является инструментом для решения проблемы достижимости. Пусть маркировка M’ достижима из M₀, тогда существует последовательность (возможно пустая) запусков переходов G, которая приводит из M₀ к M’. Это означает, что f(G) является неотрицательным целым решением следующего матричного уравнения для X:

 

M’ = M₀ + X Д  (*)

 

Следовательно, если M’ достижима из M₀, тогда уравнение (*) имеет решение в неотрицательных целых; если уравнение не имеет решения, тогда M’ недопустима из M₀.

ПРИМЕР:

1	1	1	0
0	0	0	1
0	0	1	0

 

                                                               Д^- =

 

 

1	0	0	0
0	2	1	0
0	0	0	1

 

                                                            Д⁺=

 

 

0	-1	-1	0
0	+2	+1	-1
0	0	-1	+1

 

                                             Д = Д⁺ - Д^- =

 

 

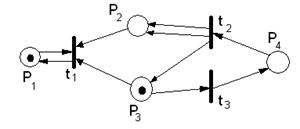
В начальной маркировке M₀=(1,0,1,0) переход t₃ разрешён и приводит к маркировке M’, где:

0	-1	-1	0
0	+2	+1	-1
0	0	-1	+1

 

M’=(1,0,1,0)+(0,0,1) =(1,0,1,0)+(0,0,-1,+1)=(1,0,0,1)                    

Последовательность G= t_­­3 t_­­2 t_­­3 t_­­2 t_­­1 представляется вектором запусков f(G)=(1,2,2) и получает маркировку M’:

 

0	-1	-1	0
0	+2	+1	-1
0	0	-1	+1

 

 M’ = (1,0,1,0) + (1,2,2)                                          =(1,0,1,0) +(0,3,-1,0) = (1,3,0,0)

 

 

Для определения того, является ли маркировка (1, 8, 0, 1) достижимой из маркировки (1, 0, 1, 0), имеем уравнение

 

0	-1	-1	0
0	+2	+1	-1
0	0	-1	+1

 

 (1, 8, 0, 1) = (1, 0, 1, 0) + X

 

0	-1	-1	0
0	+2	+1	-1
0	0	-1	+1

 

(0,8,-1,1)= X

 

 

которое имеет решение X=(0, 4, 5). Это соответствует последовательности G= t₃ t₂ t₃ t₂ t₃ t₂ t₃ t₂ t₃.

Можно показать, что маркировка (1, 7, 0, 1) недостижима из маркировки (1, 0, 1, 0) поскольку матричное уравнение

0	-1	-1	0
0	+2	+1	-1
0	0	-1	+1

 

(1,7,0,1)=(1,0,1,0) + X

 

 

0	-1	-1	0
0	+2	+1	-1
0	0	-1	+1

 

(0,7,-1,1)= X

 

 

не имеет решения.