Если об обстановке опыта можно сделать n исключающих друг друга предположений (гипотез)
H 1, H 2, …, Hn
и если событие A может появиться только при одной из этих гипотез, то вероятность события A вычисляется по формуле полной вероятности:
Р(A) = Р(H 1)Р (А | H 1) + Р(H 2)Р (А | H 2) + … + Р(Hn)Р (А | Hn)
или
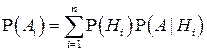 ,
,
где Р(Hi) –вероятность гипотезы Hi,Р(А | Hi) –условная вероятность события A при этой гипотезе.
Гипотезы H 1, H 2, …, Hn составляют полную группу попарно несовместных событий, т. е.
 .
.
Если до опыта вероятности гипотез были Р(H 1), Р(H 2),..., Р(Hn), а в результате опыта появилось событие A, то с учетом этого события «новые», т.е. условные, вероятности гипотез вычисляются по формуле Бейеса:
 .
.
Формула Бейеса дает возможность «пересмотреть» вероятности гипотез с учетом наблюденного результата опыта.
Если после опыта, закончившегося появлением события A, производится еще один опыт, в котором может появиться или не появиться событие В, то вероятность (условная) этого последнего события вычисляется по формуле полной вероятности, в которую подставлены не прежние вероятности гипотез Р(Hi), а новые Р(Hi | А):
 .
.
Формула Бейеса позволяет на основе знания априорных (до опыта) вероятностей гипотез P(Hi) и условных вероятностей наступления события A при этих гипотезах – P(A | Hi) вычислить апостериорные (после опыта, A наступило) вероятности гипотез P(Hi | A).
Задачи
4.1. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартная, равна 0,8, а второго – 0,9. Найти вероятность того, что наудачу взятая деталь (из наудачу взятого набора) – стандартная.
Решение. Обозначим через A событие «извлеченная деталь стандартная». Деталь может быть извлечена либо из первого набора (гипотеза H 1), либо из второго (гипотеза H 2). Вероятность того, что деталь вынута из первого набора P(H 1) = 1/2. Вероятность того, что деталь вынута из второго набора P(H 2) = 1/2. Условная вероятность того, что из первого набора будет извлечена стандартная деталь, P(A | H 1) = 0,8. Условная вероятность того, что из второго набора будет извлечена стандартная деталь, P(A | H 2) = 0,9.
Искомая вероятность того, что извлеченная наудачу деталь – стандартная, по формуле полной вероятности равна
 .
.
4.2. В первой коробке содержится 20 радиоламп, из них 18 стандартных; во второй коробке – 10 ламп, из них 9 стандартных. Из второй коробки наудачу взята лампа и переложена в первую. Найти вероятность того, что лампа, наудачу извлеченная из первой коробки, будет стандартной.
Решение. Обозначим через A событие «из первой коробки извлечена стандартная лампа». Из второй коробки могла быть извлечена либо стандартная лампа (гипотеза H 1), либо нестандартная (гипотеза H 2). Вероятность того, что из второй коробки извлечена стандартная лампа, P(H 1) = 9/10=0,9.
Вероятность того, что из второй коробки извлечена нестандартная лампа, P(H 2) = 1/10=0,1.
Условная вероятность того, что из первой коробки извлечена стандартная лампа, при условии, что из второй коробки в первую была переложена стандартная лампа, равна P(A | H 1) = 19/21.
Условная вероятность того, что из первой коробки извлечена стандартная лампа, при условии, что из второй коробки в первую была переложена нестандартная лампа, равна P(A | H 2) = 18/21.
Искомая вероятность того, что из первой коробки будет извлечена стандартная лампа, по формуле полной вероятности равна
 .
.
Аналогично решаются задачи 4.5 – 4.10.
4.3. В группе из 10 студентов, пришедших на экзамен, 3 подготовленных отлично, 4 – хорошо, 2 – посредственно и 1 – плохо. В экзаменационных билетах имеется 20 вопросов. Отлично подготовленный студент может ответить на все 20 вопросов, хорошо подготовленный – на 16, посредственно – на 10, плохо – на 5. Вызванный наугад студент ответил на три произвольно заданных вопроса. Найти вероятность того, что этот студент подготовлен: а) отлично; б) плохо.
Решение. Гипотезы:
Н 1 – студент подготовлен отлично;
Н 2 – студент подготовлен хорошо;
Н 3 – студент подготовлен посредственно;
Н 4 – студент подготовлен плохо.
До опыта (априори):
P(H 1) = 0,3; P(H 2) = 0,4; P(H 3) = 0,2; P(H 4) = 0,1;
P(A | H 1) = 1; P(A | H 2) = (16/20)∙(15/19)∙(14/18) ≈ 0,491;
P(A | H 3) = (10/20)∙(9/19)∙(8/18) ≈ 0,105;
P(A | H 4) = (5/20)∙(4/19)∙(3/18) ≈ 0,009.
Вычислим знаменатель в формуле Бейеса (формула полной вероятности)
P(A)=0,3∙1+0,4∙0,491+0,2∙0,105+0,1∙0,009 = 0,518.
После опыта (апостериори):
а)  ; б)
; б)  .
.
4.4. Детали, изготовленные цехом завода, попадают для проверки к одному из двух контролеров. Вероятность того, что деталь попадет к первому контролеру, равна 0,6, а ко второму – 0,4. Вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0,94, а вторым – 0,98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер.
Решение. Обозначим через A событие, состоящее в том, что годная деталь признана стандартной. Можно сделать два предположения:
1) деталь проверил первый контролер (гипотеза H 1);
2) деталь проверил второй контролер (гипотеза H 2).
Искомую вероятность того, что деталь проверил первый контроллер, найдем по формуле Бейеса:
 .
.
По условию задачи имеем:
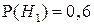 (вероятность того, что деталь попадет к первому контролеру);
(вероятность того, что деталь попадет к первому контролеру);
 вероятность того, что деталь попадет ко второму контролеру);
вероятность того, что деталь попадет ко второму контролеру);
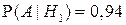 (вероятность того, что годная деталь будет признана первым контролером стандартной);
(вероятность того, что годная деталь будет признана первым контролером стандартной);
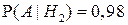 (вероятность того, что годная деталь будет признана вторым контролером стандартной).
(вероятность того, что годная деталь будет признана вторым контролером стандартной).
Искомая вероятность
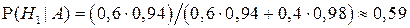 .
.
Как видно, до испытания вероятность гипотезы H 1 (априорная) равнялась 0,6, а после того, как стал известен результат испытания, вероятность этой гипотезы (апостериорная) изменилась и стала равна 0,59. Таким образом, использование формулы Бейеса позволило переоценить вероятность рассматриваемой гипотезы.
Аналогично решаются задачи 4.11 – 4.13.
4.5. У сборщика имеется 16 деталей, изготовленных заводом № 1, и 4 детали завода № 2. Наудачу взяты 2 детали. Найти вероятность того, что хотя бы одна из них окажется изготовленной заводом № 1.
Ответ: 92/95.
4.6. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника – 0,9, для велосипедиста – 0,8 и для бегуна – 0,76. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму.
Ответ: 0,86.
4.7. Сборщик получил 3 коробки деталей, изготовленных заводом № 1, и 2 коробки деталей, изготовленных заводом № 2. Вероятность того, что деталь завода № 1 стандартна, равна 0,8, а завода № 2 – 0,9. Сборщик наудачу извлек деталь из наудачу взятой коробки. Найти вероятность того, что извлечена стандартная деталь.
Ответ: 0,84.
4.8. В первом ящике содержится 20 деталей, из них 15 стандартных; во втором – 30 деталей, из них 24 стандартных; в третьем – 10 деталей, из них 6 стандартных. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика — стандартная.
Ответ: 43/60.
4.9. В телевизионном ателье имеется 4 кинескопа. Вероятности того, что кинескоп выдержит гарантийный срок службы, соответственно равны 0,8; 0,85; 0,9; 0,95. Найти вероятность того, что взятый наудачу кинескоп выдержит гарантийный срок службы.
Ответ: 0,875.
4.10. В двух ящиках имеются радиолампы. В первом ящике содержится 12 ламп, из них 1 нестандартная; во втором 10 ламп, из них 1 нестандартная. Из первого ящика наудачу взята лампа и переложена во второй. Найти вероятность того, что наудачу извлеченная из второго ящика лампа будет нестандартной.
Ответ: 13/132.
4.11. При отклонении от нормального режима работы автомата срабатывает сигнализатор С-I с вероятностью 0,8, а сигнализатор С-II срабатывает с вероятностью 1. Вероятности того, что автомат снабжен сигнализатором С-I или С-II, соответственно равны 0,6 и 0,4. Получен сигнал о разделке автомата. Что вероятнее: автомат снабжен сигнализатором С-I или С-II?
Ответ: Вероятность того, что автомат снабжен сигнализатором С-I, равна 6/11, а С-II – 5/11.
4.12. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы курса 4, из второй – 6, из третьей группы – 5 студентов. Вероятности того, что студент первой, второй и третьей группы попадает в сборную института, соответственно равны 0,9; 0,7 и 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. К какой из групп вероятнее всего принадлежал этот студент?
Ответ: Вероятности того, что выбран студент первой, второй, третьей групп, соответственно равны: 18/59, 21/59, 20/59.
4.13. Вероятность для изделий некоторого производства удовлетворять стандарту равна 0,96. Предлагается упрощенная система проверки на стандартность, дающая положительный результат с вероятностью 0,98 для изделий, удовлетворяющих стандарту, а для изделий, которые не удовлетворяют стандарту, – с вероятностью 0,05. Найти вероятность того, что изделие, признанное при проверке стандартным, действительно удовлетворяет стандарту.
Ответ: 0,998.
5. Схема испытаний Бернулли. Биномиальное распределение.
Формулы Муавра – Лапласа
Пусть проводится эксперимент, состоящий из n независимых опытов, в каждом из которых некоторое событие А либо наступает, либо не наступает. Вероятность наступления события А в каждом опыте постоянна и равна р. Такой эксперимент называется схемой испытаний Бернулли.
Вероятность того, что событие А наступит ровно m раз в схеме испытаний Бернулли
 .
.
Величина Р п (т),рассматриваемая как функция от m (m = 0, 1,..., n), называется биномиальным распределением вероятно стей, отметим, что  . Максимальное значение Р п (т)достигается при
. Максимальное значение Р п (т)достигается при 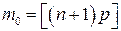 ,где [ ] – целая часть числа, m 0 называется наивероятнейшим значением. Если
,где [ ] – целая часть числа, m 0 называется наивероятнейшим значением. Если  –целое число, то наивероятнейшим значением является также и m 0 – 1. Обозначим q = 1 – р.
–целое число, то наивероятнейшим значением является также и m 0 – 1. Обозначим q = 1 – р.
В случае, когда р и q не малы, а п велико (обычно npq > 8), применяют приближенные формулы Муавра – Лапласа
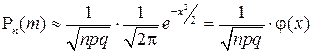 ,
,
где  , а
, а 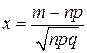 ;
;
 ,
,
где  – функция Лапласа.
– функция Лапласа.
Задачи
5.1. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит нормы, равна p = 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
Решение. Вероятность нормального расхода электроэнергии в продолжение каждых из 6 суток постоянна и равна p = 0,75. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна
q = 1 – p = 1 – 0,75 = 0,25.
Искомая вероятность по формуле Бернулли равна
 .
.
5.2. Что вероятнее: выиграть у равносильного противника (ничейный исход партии исключен): а) три партии из четырех или пять из восьми; б) не менее трех партий из четырех или не менее пяти партий из восьми?
Решение. Так как противники равносильные, то вероятности выигрыша и проигрыша каждой партии одинаковы и равны p = q = 1/2.
а) Вероятность выиграть три партии из четырех
 .
.
Вероятность выиграть пять партий из восьми
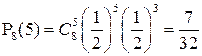 .
.
Так как 1/4 > 7/32, то вероятнее выиграть три партии из четырех.
б) Вероятность выиграть не менее трех партий из четырех
 ,
,
а вероятность выиграть не менее пяти партий из восьми
 .
.
Так как 93/256 > 5/18 = 80/256, то вероятнее выиграть не менее пяти партий из восьми.
Аналогично решаются задачи 5.5 – 5.10.
5.3. Найти вероятность того, что событие A наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.
Решение. По условию, n = 400; m = 80; p = 0,2; q = 0,8.
Воспользуемся асимптотической формулой Лапласа:
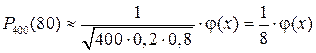 .
.
Вычислим определяемое данными задачи значение x:
 .
.
По таблице 1 находим φ(0) = 0,3989.
Искомая вероятность
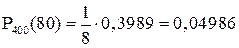 .
.
Замечание. Для отрицательных значений аргумента x функции φ(x) пользуются той же таблицей, так как функция φ(x) четная, т.е. φ(– x) = φ(x).
Аналогично решаются задачи 5.11 – 5.12.
5.4. Вероятность того, что деталь не прошла проверку ОТК, равна p = 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.
Решение. По условию, p = 0,2; q = 0,8; n = 400; m 1 = 70; m 2 = 100. воспользуемся интегральной теоремой Лапласа:
 .
.
Вычислим нижний и верхний пределы интегрирования:
 ;
;
 .
.
Таким образом, имеем
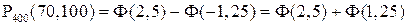 .
.
По таблице 2 находим: Φ(2,5) = 0,4938; Φ(1,25) = 0,3944.
Искомая вероятность
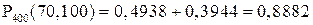 .
.
Замечание. В таблице 2 даны значения функции Φ(x) для положительных значений x и для x = 0; для x < 0 пользуются той же таблицей, так как функция Φ(x) нечетная, т.е. Φ(– x) = – Φ(x). В таблице приведены значения интеграла лишь до x = 5, так как для x > 5 можно принять Φ(x) = 0,5.
Аналогично решаются задачи 5.13 – 5.14.
5.5. В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент: а) включено 4 мотора; б) включены все моторы; в) выключены все моторы.
Ответ: а) Р6 (4) = 0,246; б) Р6(6) = 0,26; в) Р6 (0) = 0,000064.
5.6. Найти вероятность того, что событие А появится в пяти независимых испытаниях не менее двух раз, если в каждом испытании вероятность появления события А равна 0,3.
Ответ: Р = 1 – [Р5(0) + Р5(1)] = 0,472.
5.7. Событие В появится в случае, если событие А появится не менее двух раз. Найти вероятность того, что наступит событие В, если будет произведено 6 независимых испытаний, в каждом из которых вероятность появления события А равна 0,4.
Ответ: Р = 1 – [Р6(0) + Р6(1)] = 0,767.
5.8. Произведено 8 независимых испытаний, в каждом из которых вероятность появления события А равна 0,1. Найти вероятность того, что событие А появится хотя бы 2 раза.
Ответ: Р = 1 – [Р8(0) + Р8(1)] = 0,19.
5.9. Монету бросают 6 раз. Найти вероятность того, что герб выпадет: а) менее двух раз; б) не менее двух раз.
Ответ: Р = Р6(0) + Р6(1) = 7/64; Q = 1 – [Р6(0) + Р6(1)] = 57/64.
5.10. Вероятность попадания в цель при одном выстреле из орудия р = 0,9. Вероятность поражения цели при k попаданиях  равна
равна  . Найти вероятность того, что цель будет поражена, если сделано два выстрела.
. Найти вероятность того, что цель будет поражена, если сделано два выстрела.
Указание. Воспользоваться формулами Бернулли и полной вероятности.
Ответ: 0,9639.
5.11. Найти приближенно вероятность того, что при 400 испытаниях событие наступит ровно 104 раза, если вероятность его появления в каждом испытании равна 0,2.
Ответ: Р400(104) = 0,0006.
5.12. Вероятность появления успеха в каждом испытании равна 0,25. Какова вероятность, что при 300 испытаниях успех наступит: а) ровно 75 раз; б) ровно 85 раз.
Ответ: а) 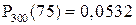 ; б)
; б)  .
.
5.13. Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, что при 100 выстрелах мишень будет поражена: а) не менее 70 и не более 80 раз; б) не более 70 раз.
Ответ: а) Р100(70, 80) = 2Ф(1,16) =0,7498;
б) Р100(0; 70)= – Ф(1,15) + 0,5 = 0,1251.
5.14. Какова вероятность того, что из 100 наугад отобранных монет число монет, расположенных «гербом» вверх, будет от 45 до 55.
Ответ:  .
.
Таблица значений функции 
| x
| 0
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
|
| 0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
| 0,3989
3970
3910
3814
3683
3521
3332
3123
2897
2661
| 3989
3965
3902
3802
3668
3503
3312
3101
2874
2637
| 3989
3961
3894
3790
3653
3485
3292
3079
2850
2613
| 3988
3956
3885
3778
3637
3467
3271
3056
2827
2589
| 3986
3951
3876
3765
3621
3448
3251
3034
2803
2565
| 3984
3945
3867
3752
3605
3429
3230
3011
2780
2541
| 3982
3939
3857
3739
3589
3410
3209
2989
2756
2516
| 3980
3932
3847
3726
3572
3391
3187
2966
2732
2492
| 3977
3925
3836
3712
3555
3372
3166
2943
2709
2468
| 3973
3918
3825
3697
3538
3352
3144
2920
2685
2444
|
| 1,0
1,1
1.2
1,3
1,4
1.5
1,6
1,7
1,8
1,9
| 0,2420
2179
1942
1714
1497
1295
1109
0940
0790
0656
| 2396
2155
1919
1691
1476
1276
1092
0925
0775
0644
| 2371
2131
1895
1669
1456
1257
1074
0909
0761
0632
| 2347
2107
1872
1647
1435
1238
1057
0893
0748
0620
| 2323
2083
1849
1626
1415
1219
1040
0878
0734
0608
| 2299
2059
1826
1604
1394
1200
1023
0863
0721
0596
| 2275
2036
1804
1582
1374
1182
1006
0848
0707
0584
| 2251
2012
1781
1561
1354
1163
0989
0833
0694
0573
| 2227
1989
1758
1539
1334
1145
0973
0818
0681
0562
| 2203
1965
1736
1518
1315
1127
0957
0804
0669
0551
|
| 2,0
2,1
2,2
2,3
2.4
2,5
2,6
2,7
2,8
2,9
| 0,0540
0440
0355
0283
0224
0175
0136
0104
0079
0060
| 0529
0431
0347
0277
0219
0171
0132
0101
0077
0058
| 0519
0422
0339,
0270
0213
0167
0129
0099
0075
0056
| 0508
0413
0332
0264
0208
0163
0126
0096
0073
0055
| 0498
0404
0325
0258
0203
0158
0122
0093
0071
0053
| 0488
0396
0317
0252
0198
0154
0119
0091
0069
0051
| 0478
0387
0310
0246
0194
0151
0116
0088
0067
0050
| 0468
0379
0303
0241
0189
0147
0113
0086
0065
0048
| 0459
0371
0297
0235
0184
0143
0110
0084
0063
0047
| 0449
0363
0290
0229
0180
0139
0107
0081
0061
0046
|
| 3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
| 0,0044
0033
0024
0017
0012
0009
0006
0004
0003
0002
| 0043
0032
0023
0017
0012
0008
0006
0004
0003
0002
| 0042
0031
0022
0016
0012
0008
0006
0004
0003
0002
| 0040
0030
0022
0016
0011
0008
0005
0004
0003
0002
| 0039
0029
0021
0015
0011
0008
0005
0004
0003
0002
| 0038
0028
0020
0015
0010
0007
0005
0004
0002
0002
| 0037
0027
0020
0014
0010
0007
0005
0003
0002
0002
| 0036
0026
0019
0014
0010
0007
0005
0003
0002
0002
| 0035
0025
0018
9013
0009
0007
0005
0003
0002
0001
| 0034
0025
0018
0013
0009
0006
0004
0003
0002
0001
|
Таблица значений функции 
| x
| 0
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
|
| 0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
| 0,00000
03983
07926
11791
15542
19146
22575
25804
28814
31594
| 00399
04380
08317
12172
15910
19497
22907
26115
29103
31859
| 00798
04776
08706
12552
16276
19847
23237
26424
29389
32121
| 01197
05172
09095
12930
16640
20194
23565
26730
29673
32381
| 01595
05567
09483
13307
17003
20540
23891
27035
29955
32639
| 01994
05962
09871
13683
17364
20884
24215
27337
30234
32894
| 02392
06356
10257
14058
17724
21226
24537
27637
30511
33147
| 02790
06749
10642
14431
18082
21566
24857
27935
30785
33398
| 03188
07142
11026
14803
18439
21904
25175
28230
31057
33646
| 03586
07535
11409
15173
18793
22240
25490
28524
31327
33891
|
| 1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
| 34134
36433
38493
40320
41924
43319
44520
45543
46407
47128
| 34375
36650
38686
40490
42073
43448
44630
45637
46485
47193
| 34614
36864
38877
40658
42220
43574
44738
45728
46562
47257
| 34850
37076
39065
40824
42364
43699
44845
46818
46638
47320
| 35083
37286
39251
40988
42507
43822
44950
45907
46712
47381
| 35314
37493
39435
41149
42647
43943
45053
45994
46784
47441
| 35543
37698
39617
41309
42786
44062
45154
46080
46856
47500
| 35769
37900
39796
41466
42922
44179
45254
46164
46926
47558
| 35993
38100
39973
41621
43056
44295
45352
46246
46995
47615
| 36214
38298
40147
41774
43189
44408
45449
46327
47062
47670
|
| 2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
| 47725
48214
48610
48928
49180
49379
49534
49653
49744
49813
| 47778
48257
48645
48956
49202
49396
49547
49664
49752
49819
| 47831
48300
48679
48983
49224
49413
49560
49674
49760
49825
| 47882
48341
48713
49010
49245
49430
49573
49683
49767
49831
| 47932
48382
48745
49036
49266
49446
49585
49693
49774
49836
| 47982
48422
48778
49061
49286
49461
49598
49702
49781
49841
| 48030
48461
48809
49086
49305
49477
49609
49711
49788
49846
| 48077
48500
48840
49111
49324
49492
49621
49720
49795
49851
| 48124
48537
48870
49134
49343
49506
49632
49728
49801
49856
| 48169
48574
48899
49158
49361
49520
49643
49736
49807
49861
|
| 3,0
3,5
4,0
4,5
5,0
| 0,49835
49977
499968
499997
49999997
| 3,1
3,6
| 49903
49984
| 3,2
3,7
| 49931
49989
| 3,3
3,8
| 49952
49993
| 3,4
3,9
| 49966
49995
|
| | | | | | | | | | | | |
Литература
1. Вентцель Е.С. Задачи и упражнения по теории вероятностей: учеб. пособие для втузов / Е.С. Вентцель, Л.А. Овгоров. – 3-е изд., стер. – М.: Высшая школа, 2000. – 366 с.
2. Гмурман В.Е. Теория вероятностей и математическая статистика: учеб. пособие для втузов / В.Е. Гмурман. – 10-е изд., стер. – М.: Высшая школа, 2004. – 479 с.
3. Сборник задач по теории вероятностей, математической статистике и теории случайных функций / под ред. А.А. Свешникова. – М.: Наука, 1965. – 632 с.
[*] Данная задача, как и ряд других в главе 3, может быть решена и с помощью непосредственного подсчета числа случаев; здесь требуется решить их с помощью теорем сложения или умножения.



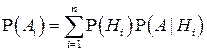 ,
, .
. .
. .
. .
. .
. ; б)
; б)  .
.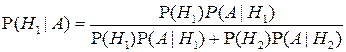 .
.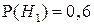 (вероятность того, что деталь попадет к первому контролеру);
(вероятность того, что деталь попадет к первому контролеру); вероятность того, что деталь попадет ко второму контролеру);
вероятность того, что деталь попадет ко второму контролеру);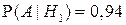 (вероятность того, что годная деталь будет признана первым контролером стандартной);
(вероятность того, что годная деталь будет признана первым контролером стандартной);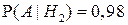 (вероятность того, что годная деталь будет признана вторым контролером стандартной).
(вероятность того, что годная деталь будет признана вторым контролером стандартной).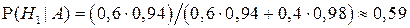 .
. .
. . Максимальное значение Р п (т)достигается при
. Максимальное значение Р п (т)достигается при 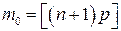 ,где [ ] – целая часть числа, m 0 называется наивероятнейшим значением. Если
,где [ ] – целая часть числа, m 0 называется наивероятнейшим значением. Если  –целое число, то наивероятнейшим значением является также и m 0 – 1. Обозначим q = 1 – р.
–целое число, то наивероятнейшим значением является также и m 0 – 1. Обозначим q = 1 – р.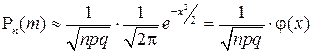 ,
, , а
, а 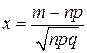 ;
; ,
, – функция Лапласа.
– функция Лапласа. .
. .
.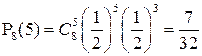 .
. ,
, .
.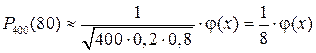 .
. .
.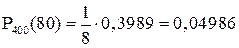 .
. .
. ;
; .
.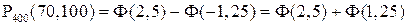 .
.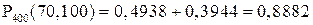 .
. равна
равна  . Найти вероятность того, что цель будет поражена, если сделано два выстрела.
. Найти вероятность того, что цель будет поражена, если сделано два выстрела.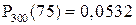 ; б)
; б)  .
. .
.




