1. Даны векторы  и
и  . Найти координаты вектора
. Найти координаты вектора  .
.
1) 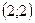 ; 2)
; 2)  ; 3) 4; 4)
; 3) 4; 4)  ; 5)
; 5) 
2. Длина вектора 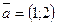 равна:
равна:
1) 1; 2)  ; 3) 2; 4)
; 3) 2; 4)  ; 5)
; 5)  .
.
3. Скалярное произведение векторов  и
и  равно:
равно:
1) 14; 2) 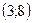 ; 3) 11; 4)
; 3) 11; 4)  ; 5)
; 5) 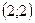
4. Даны точки  и
и  . Найти координаты вектора
. Найти координаты вектора  .
.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 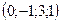 ; 5)
; 5) 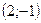
5. Дан вектор 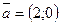 . Найти координаты вектора
. Найти координаты вектора  .
.
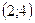 ; 2) 6; 3)
; 2) 6; 3) 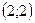 ; 4)
; 4)  ; 5)
; 5) 
6. Найти площадь треугольника с вершинами в точках  ,
,  ,
,  .
.
1). 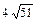 ; 2).
; 2).  ; 3).
; 3).  ; 4).
; 4).  5).
5). 
7. Известно, что  ,
,  , а угол между
, а угол между  и
и  равен
равен  . Найти
. Найти  .
.
1). 0; 2).  ; 3).
; 3). 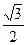 ; 4).
; 4). 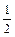 5). 1.
5). 1.
8. Определить  , при котором компланарны векторы
, при котором компланарны векторы  ,
, 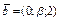 ,
,  .
.
1).  ; 2).
; 2). 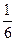 ; 3). 1; 4).
; 3). 1; 4).  ; 5).
; 5). 
9. Найти объем треугольной пирамиды с вершинами в точках  ,
,  ,
,  ,
, 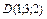 .
.
1). 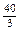 ; 2).
; 2).  ; 3).
; 3). 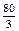 ; 4). 40; 5).
; 4). 40; 5).  .
.
10. 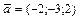 ,
, 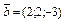 . Найти
. Найти  .
.
1).  ; 2).
; 2). 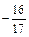 ; 3).
; 3).  ; 4). 0; 5).
; 4). 0; 5).  .
.
РАЗДЕЛ III. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ
Глава 4. УРАВНЕНИЕ ЛИНИИ
Простейшие задачи аналитической геометрии на плоскости. Линии первого порядка
Длина отрезка между точками  и
и  находится по формуле:
находится по формуле:
 -
-
Координаты точки деления отрезка в данном отношении:
 ;
;  -
-
1. Уравнение прямой линии с угловым коэффициентом:

Где k равен тангенсу угла α, наклона прямой к оси Ох ( ) и называется угловым коэффициентом прямой, b – величина отрезка отсекаемого прямой на оси Оу.
) и называется угловым коэффициентом прямой, b – величина отрезка отсекаемого прямой на оси Оу.
2. Уравнение прямой, проходящей через две точки  и
и  :
:

3. Уравнение прямой, проходящей через данную точку 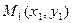 с данным угловым коэффициентом:
с данным угловым коэффициентом:

4. Общее уравнение прямой - уравнение первой степени с двумя неизвестными.

где А, В, С - произвольные коэффициенты (А и В не равны одновременно).
5. Угол между двумя прямыми. Если известны угловые коэффициенты двух прямых, то один из углов между этими прямыми определяется по формуле:
 ,
,  -угол между двумя прямыми.
-угол между двумя прямыми.
Второй угол равен 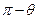
Условие параллельности двух прямых: 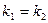 .
.
Условие перпендикулярности двух прямых  .
.
6. Уравнение прямой, проходящей через т.  , перпендикулярно вектору
, перпендикулярно вектору  определяется по формуле:
определяется по формуле:
 -
-
Линии второго порядка
Определение. Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружности.
Окружность радиуса R с центром в точке М0 (х0; у0) имеет уравнение:

Уравнение окружности с центром в т. O ( 0; 0 ) и радиусом r имеет вид:
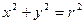

Определение. Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, называемых фокусамиэллипса, есть величина постоянная. Фокусы эллипса обозначаются буквами F1 и F2, расстояние между ними  через 2с.
через 2с.
Каноническое (простейшее) уравнение эллипса имеет вид:
 где: b 2 = a 2 - c 2 т.е.
где: b 2 = a 2 - c 2 т.е. 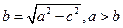
Если эллипс задан каноническим уравнением, то его осями симметрии служат оси Ох и Оу, а начало координат - центр симметрии.
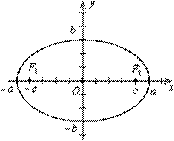
Точки пересечения эллипса с его осями симметрии называются вершинами эллипса. Центр симметрии - центром эллипса. Отрезок между двумя вершинами, содержащий фокусы, называется большой осью эллипса и обозначается 2а, половина его длины - большой полуосью эллипса и обозначается а. Отрезок между вершинами на оси симметрии, не содержащей фокусов, называется малой осью эллипса и обозначается 2 b, половина его длины - малой полуосью и обозначается b.
Величина с, являющаяся половиной расстояния между фокусами, определяется из формулы:

Величина 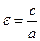 , (0< ε <1) называется эксцентриситетом эллипса.
, (0< ε <1) называется эксцентриситетом эллипса.
Эксцентриситет  эллипса характеризует степень вытянутости эллипса. Чем ближе эксцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс.
эллипса характеризует степень вытянутости эллипса. Чем ближе эксцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс.
Определение. Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная.
Каноническое уравнение гиперболы с центром в начале координат имеет вид:
 где b 2= c 2- a 2 т.е.
где b 2= c 2- a 2 т.е. 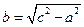
Уравнение гиперболы со смещённым центром О1(x 0, y 0):
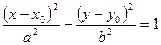
Прямые  называются асимптотами гиперболы.
называются асимптотами гиперболы.

Точки пересечения гиперболы с осью Ох, заданной каноническим уравнением, называются вершинами гиперболы, отрезок между ними называется действительной осью гиперболы.
Отрезок оси ординат между точками (0; - b) и (0; b) называется мнимой осью.
Числа a и b называются соответственно действительной и мнимой полуосями гиперболы. Начало координат называется ее центром.
Величина  , (ε >1) называется эксцентриситетом гиперболы.
, (ε >1) называется эксцентриситетом гиперболы.
Определение. Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы
Каноническое уравнение параболы с вершиной в т. O ( 0,0 ) имеет вид:
 где р - параметр параболы
где р - параметр параболы
Точка пересечения оси симметрии с параболой называется вершиной параболы, и находится в начале координат. Симметрична относительно оси Ох. Парабола имеет фокус 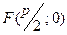 и директрису
и директрису 

Парабола  симметрична относительно оси Оу, лежит в верхней полуплоскости.
симметрична относительно оси Оу, лежит в верхней полуплоскости.
Примеры решения типовых задач
№ 1. Даны координаты вершин треугольника А ВС: А (4; 3), В (16; - 6), С (20; 16).
Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) угол В в радианах с точностью до двух знаков; 4) уравнение высоты CD и ее длину; 5) уравнение медианы АЕ и координаты точки К пересечения этой медианы с высотой CD; 6) уравнение прямой, проходящей через точку Кпараллельно стороне АВ.
Решение.
1. Расстояние d между точками А (x 1; y 1) и В (х2; y 2) определяется по формуле:
 (1)
(1)
Применяя (1), находим длину стороны АВ:

2. Уравнение прямой, проходящей через точки А(х1; у1) и В(х2; y 2), имеет вид:  (2)
(2)
Подставляя в (2) координаты точек A и В, получим уравнение стороны АВ:



4 y -12= -3 x +12;
3x+4y-24=0 (AB).
Решив последнее уравнение относительно у, находим уравнение стороны АВ в виде уравнения прямой с угловым коэффициентом:
4 y = -3 x +24;  откуда
откуда 
Подставив в (2) координаты точек В и С, получим уравнение прямой BC:


 ;
;
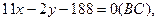 или y =5,5 x -94, откуда kBC =5,5.
или y =5,5 x -94, откуда kBC =5,5.
3. Известно, что тангенс угла  между двумя прямыми, угловые коэффициенты которых соответственно равны k1 и k2 вычисляется по формуле:
между двумя прямыми, угловые коэффициенты которых соответственно равны k1 и k2 вычисляется по формуле:
 (3)
(3)
Искомый угол В образован прямыми АВ и ВС, угловые коэффициенты которых найдены: 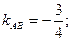
 Применяя (3), получим
Применяя (3), получим

В=63°26'. или В» 1,11 рад.
4. Уравнение прямой, проходящей через данную точку в заданном направлении, имеет вид:
y — y 1 = k (x — x 1). (4)
Высота CD перпендикулярна стороне АВ. Чтобы найти угловой коэффициент высоты CD, воспользуемся условием перпендикулярности прямых. Так как,  , то
, то  . Подставив в (4) координаты точки С и найденный угловой коэффициент высоты, получим:
. Подставив в (4) координаты точки С и найденный угловой коэффициент высоты, получим:


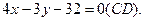
Чтобы найти длину высоты CD, определим сперва координаты точки D - точки пересечения прямых АВ и CD. Решая совместно систему:
 , находим x =8, y =0, т.е D (8;0)
, находим x =8, y =0, т.е D (8;0)
По формуле (1) находим длину высоты CD:
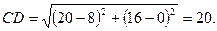
5. Чтобы найти уравнение медианы АЕ, определим сначала координаты точки Е, которая является серединой стороны ВС, применяя формулы деления отрезка на две равные части:


Следовательно, 
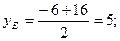 E (18;5).
E (18;5).
Подставив в (2) координаты точек А и Е, находим уравнение медианы:
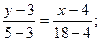


Чтобы найти координаты точки пересечения высоты CD и медианы АЕ, решим совместно систему уравнений:
 x=11, y=4; K (11;4).
x=11, y=4; K (11;4).
6. Так как искомая прямая параллельна стороне АВ, то ее угловой коэффициент будет равен угловому коэффициенту прямой АВ. Подставив в (4) координаты найденной точки К и угловой коэффициент  получим:
получим:



Треугольник ABC, высота CD, медиана АЕ, прямая KF построены в системе координат хОу на рис. 1.

№ 2. Установить, какая линия определяется данным уравнением. Изобразить данную линию на чертеже, охарактеризовав ее.
а) х2 + у2 + 6 х + 10 у – 15 = 0.
Преобразуем данное уравнение, для этого выделим полный квадрат:
 х2 + 6 х + 9 + у2 + 10 у – 9 – 25 - 15 = 0;
х2 + 6 х + 9 + у2 + 10 у – 9 – 25 - 15 = 0;
(х + 3 )2 + (у + 5 )2 - 49 = 0 – уравнение окружности с центром в точке (- 3; - 5), радиусом 7.
 у
у
х
О (- 3; - 5)
б) x 2 -4 x +4 y 2 =0.
Найдем каноническое уравнение кривой, для этого сделаем преобразования:
x 2 -4 x +4-4+4 y 2 =0 (x -2)2+4 y 2 =4
Окончательно 
Полученное уравнение есть каноническое уравнение эллипса, где а =2; b=1;
центр эллипса в точке (2,0).

Найдем фокусы, для этого вычислим параметр с:

тогда:  эксцентриситет эллипса -
эксцентриситет эллипса - 



 и
и  . Найти координаты вектора
. Найти координаты вектора  .
.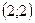 ; 2)
; 2)  ; 3) 4; 4)
; 3) 4; 4)  ; 5)
; 5) 
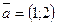 равна:
равна: ; 3) 2; 4)
; 3) 2; 4)  ; 5)
; 5)  .
. и
и  равно:
равно: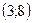 ; 3) 11; 4)
; 3) 11; 4)  ; 5)
; 5)  и
и  . Найти координаты вектора
. Найти координаты вектора  .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 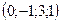 ; 5)
; 5) 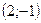
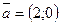 . Найти координаты вектора
. Найти координаты вектора  .
.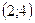 ; 2) 6; 3)
; 2) 6; 3) 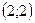 ; 4)
; 4)  ; 5)
; 5) 
 ,
,  ,
,  .
.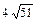 ; 2).
; 2).  ; 3).
; 3).  ; 4).
; 4).  5).
5). 
 ,
,  , а угол между
, а угол между  и
и  равен
равен  . Найти
. Найти  .
. ; 3).
; 3). 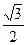 ; 4).
; 4). 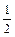 5). 1.
5). 1. , при котором компланарны векторы
, при котором компланарны векторы  ,
, 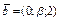 ,
,  .
. ; 2).
; 2). 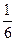 ; 3). 1; 4).
; 3). 1; 4).  ; 5).
; 5). 
 ,
,  ,
,  ,
, 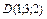 .
.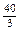 ; 2).
; 2).  ; 3).
; 3). 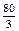 ; 4). 40; 5).
; 4). 40; 5).  .
.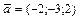 ,
, 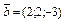 . Найти
. Найти  .
. ; 2).
; 2). 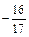 ; 3).
; 3).  ; 4). 0; 5).
; 4). 0; 5).  .
. и
и  находится по формуле:
находится по формуле: -
- ;
;  -
-
 ) и называется угловым коэффициентом прямой, b – величина отрезка отсекаемого прямой на оси Оу.
) и называется угловым коэффициентом прямой, b – величина отрезка отсекаемого прямой на оси Оу. и
и  :
:
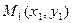 с данным угловым коэффициентом:
с данным угловым коэффициентом:

 ,
,  -угол между двумя прямыми.
-угол между двумя прямыми.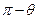
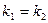 .
. .
.  , перпендикулярно вектору
, перпендикулярно вектору  определяется по формуле:
определяется по формуле: -
-
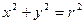

 через 2с.
через 2с. где: b 2 = a 2 - c 2 т.е.
где: b 2 = a 2 - c 2 т.е. 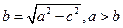


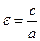 , (0< ε <1) называется эксцентриситетом эллипса.
, (0< ε <1) называется эксцентриситетом эллипса. эллипса характеризует степень вытянутости эллипса. Чем ближе эксцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс.
эллипса характеризует степень вытянутости эллипса. Чем ближе эксцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. где b 2= c 2- a 2 т.е.
где b 2= c 2- a 2 т.е. 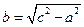
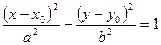
 называются асимптотами гиперболы.
называются асимптотами гиперболы.
 , (ε >1) называется эксцентриситетом гиперболы.
, (ε >1) называется эксцентриситетом гиперболы. где р - параметр параболы
где р - параметр параболы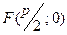 и директрису
и директрису 

 симметрична относительно оси Оу, лежит в верхней полуплоскости.
симметрична относительно оси Оу, лежит в верхней полуплоскости. (1)
(1)
 (2)
(2)


 откуда
откуда 


 ;
;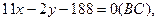 или y =5,5 x -94, откуда kBC =5,5.
или y =5,5 x -94, откуда kBC =5,5. между двумя прямыми, угловые коэффициенты которых соответственно равны k1 и k2 вычисляется по формуле:
между двумя прямыми, угловые коэффициенты которых соответственно равны k1 и k2 вычисляется по формуле: (3)
(3)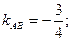
 Применяя (3), получим
Применяя (3), получим
 , то
, то  . Подставив в (4) координаты точки С и найденный угловой коэффициент высоты, получим:
. Подставив в (4) координаты точки С и найденный угловой коэффициент высоты, получим:

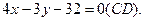
 , находим x =8, y =0, т.е D (8;0)
, находим x =8, y =0, т.е D (8;0) 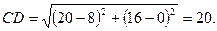



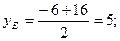 E (18;5).
E (18;5).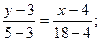


 x=11, y=4; K (11;4).
x=11, y=4; K (11;4). получим:
получим:



 у
у


 эксцентриситет эллипса -
эксцентриситет эллипса - 



