Курсовая работа
Матричные дифференциальные уравнения
Выполнила: студентка 2 курса
факультета математики и
информационных технологий
заочной формы обучения
группы Z3,5ПМИ 21
Нуркиева Р.Р.
Научный руководитель:
к.ф.-м.н.,доцент кафедры
матем.анализа
Сабитова Ю.К.
Стерлитамак - 2019
Содержание
Введение. 3
Матричные многочленные уравнения. 4
Квадратный корень из матрицы.. 19
Линейное дифференциальное уравнение. 34
Заключение. 45
Список использованных источников и литературы. 46
Введение
Эта работа полностью посвящена матричным уравнениям. Здесь излагается достаточно широкий круг вопросов теории и приложений таких уравнений.
Теоретические вопросы относятся в основном к методам практического построения решений. Рассматриваются методы точного аналитического решения.
Для достижения этих целей нам потребуются некоторые факты о способах решения различных многочленных матричных уравнений. В одних случаях они тривиальны, в других требуется соответствующее обоснование. Хотя многие из приводимых ниже результатов без особого труда распространяются на случай прямоугольных матриц, мы этими обобщениями увлекаться не будем, а всюду в дальнейшем ограничимся анализом уравнений.
Цель курсовой работы
Изучить теорию матричных дифференциальных уравнений.
1) рассмотреть примеры матричных дифференциальных уравнений и методов решения.
2) изучить перестановочные матрицы, задача Фробениуса.
3) рассмотреть частное решение неоднородного уравнения, Формула Коши.
Квадратный корень из матрицы
В этом и следующем параграфах будем рассматривать алгебраическое уравнение Риккати
 (2.1)
(2.1)
где R, А, В и Р — заданные постоянные матрицы порядка n, а θ — матрица с нулевыми элементами. Сначала рассмотрим наиболее простой частный случай, который представляет и самостоятельный интерес. Речь идет об уравнении вида
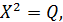 (2.2)
(2.2)
которое получается из уравнения (2.1) при  .
.
Его решение удобно рассматривать, последовательно анализируя следующие частные случаи.
1) Q имеет каноническую жорданову форму  , где
, где  , а
, а
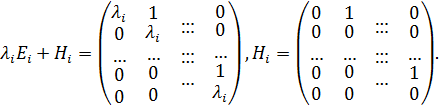
При этом все собственные значения  , матрицы Q отличны от нуля.
, матрицы Q отличны от нуля.
2) Матрица Q не имеет канонической жордановой формы, но не является особенной.
3) Q — особенная матрица.
Курсовая работа
Матричные дифференциальные уравнения
Выполнила: студентка 2 курса
факультета математики и
информационных технологий
заочной формы обучения
группы Z3,5ПМИ 21
Нуркиева Р.Р.
Научный руководитель:
к.ф.-м.н.,доцент кафедры
матем.анализа
Сабитова Ю.К.
Стерлитамак - 2019
Содержание
Введение. 3
Матричные многочленные уравнения. 4
Квадратный корень из матрицы.. 19
Линейное дифференциальное уравнение. 34
Заключение. 45
Список использованных источников и литературы. 46
Введение
Эта работа полностью посвящена матричным уравнениям. Здесь излагается достаточно широкий круг вопросов теории и приложений таких уравнений.
Теоретические вопросы относятся в основном к методам практического построения решений. Рассматриваются методы точного аналитического решения.
Для достижения этих целей нам потребуются некоторые факты о способах решения различных многочленных матричных уравнений. В одних случаях они тривиальны, в других требуется соответствующее обоснование. Хотя многие из приводимых ниже результатов без особого труда распространяются на случай прямоугольных матриц, мы этими обобщениями увлекаться не будем, а всюду в дальнейшем ограничимся анализом уравнений.
Цель курсовой работы
Изучить теорию матричных дифференциальных уравнений.
1) рассмотреть примеры матричных дифференциальных уравнений и методов решения.
2) изучить перестановочные матрицы, задача Фробениуса.
3) рассмотреть частное решение неоднородного уравнения, Формула Коши.
Матричные многочленные уравнения.
1.1. Уравнение  . Будем рассматривать уравнение
. Будем рассматривать уравнение
 , (1.1)
, (1.1)
где θ — нулевая матрица, а А и В — заданные n-мерные матрицы.
Пусть
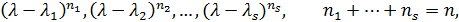

- элементарные делители матриц А и В, соответственно. Тогда существуют неособенные (невырожденные) матрицы U и V такие, что А и В приводятся к канонической жордановой форме:
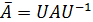 ,
, 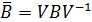 , (1.2)
, (1.2)
где

 (1.3)
(1.3)
Здесь  — единичная матрица порядка q,
— единичная матрица порядка q,
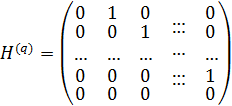 . (1.4)
. (1.4)
Умножим обе части уравнения (1.1) слева на U и справа на 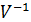 . Тогда получим
. Тогда получим 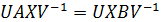 . Очевидно, что это уравнение можно переписать в виде
. Очевидно, что это уравнение можно переписать в виде
 (1.5)
(1.5)
поскольку справедливы равенства 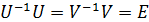 .
.
Если ввести обозначение
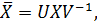 (1.6)
(1.6)
то уравнение (1.5) принимает вид
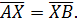 (1.7)
(1.7)
Для решения этого уравнения матрицу  разобьем на блоки
разобьем на блоки 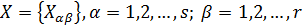 , каждый из которых является прямоугольным, но они построены так, чтобы матрица
, каждый из которых является прямоугольным, но они построены так, чтобы матрица  имела размерность
имела размерность  (
( - число строк,
- число строк,  - число столбцов).
- число столбцов).
Тогда уравнение (1.7) распадется на систему независимых друг от друга уравнений

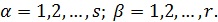
Эти уравнения перепишем в более удобной форме
 (1.8)
(1.8)
где введены обозначения
 (1.9)
(1.9)
Следовательно, 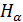 имеет порядок
имеет порядок  , а порядок матрицы
, а порядок матрицы  равен
равен  . Проанализируем каждое из полученных уравнений. Возьмем одно из них и рассмотрим возможные случаи.
. Проанализируем каждое из полученных уравнений. Возьмем одно из них и рассмотрим возможные случаи.
1-й случай. 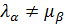 . Обе части выбранного уравнения из (1.8) умножим на
. Обе части выбранного уравнения из (1.8) умножим на  , а затем в полученном уравнении заменяем
, а затем в полученном уравнении заменяем  на
на 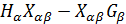 . Эту операцию повторим q — 1 раз. В итоге получим уравнение
. Эту операцию повторим q — 1 раз. В итоге получим уравнение
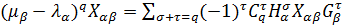 (1.10)
(1.10)
Из определения матриц 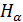 и
и  (см. (1.4) и (1.9)) следует, что
(см. (1.4) и (1.9)) следует, что
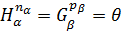 . (1.11)
. (1.11)
Поэтому если теперь в уравнении (1.10) взять  , то в каждом члене суммы,
, то в каждом члене суммы,  ,
,  . В силу равенств (1.11) либо
. В силу равенств (1.11) либо  , либо
, либо  . Так как, кроме того, в рассматриваемом случае
. Так как, кроме того, в рассматриваемом случае 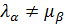 , то из уравнения (1.10) следует, что
, то из уравнения (1.10) следует, что
 (1.12)
(1.12)
2-й случай.  . В этом случае соответствующее уравнение из системы (1.8) принимает вид
. В этом случае соответствующее уравнение из системы (1.8) принимает вид
 (1.13)
(1.13)
Согласно определению (см. (1.9) и (1.4)) в матрицах 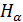 и
и  отличны от нуля только элементы первой наддиагонали (каждый из них равен единице). Все остальные элементы этих матриц — нули. Положим
отличны от нуля только элементы первой наддиагонали (каждый из них равен единице). Все остальные элементы этих матриц — нули. Положим 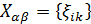 ,
,  . Тогда уравнение (1.13) можно заменить эквивалентной ему системой уравнений
. Тогда уравнение (1.13) можно заменить эквивалентной ему системой уравнений

 (1.14)
(1.14)
Полученные уравнения определяют решение, которое обладает следующими свойствами.
1) В матрице  на каждой линии, параллельной главной диагонали,стоят равные между собой элементы.
на каждой линии, параллельной главной диагонали,стоят равные между собой элементы.
2) 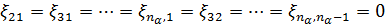 .
.
Пусть  . Из свойств 1) и 2) следует, что матрица
. Из свойств 1) и 2) следует, что матрица  квадратная. Все ее элементы, расположенные под главной диагональю, равны нулю. Элементы главной диагонали равны одному и тому же постоянному числу. Обозначим его через
квадратная. Все ее элементы, расположенные под главной диагональю, равны нулю. Элементы главной диагонали равны одному и тому же постоянному числу. Обозначим его через 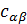 . Элементы на линии над главной диагональю равны другому постоянному числу
. Элементы на линии над главной диагональю равны другому постоянному числу  и т. д., т. е. эта матрица имеет вид (Напомним, что символ ≜ означает равенство по определению)
и т. д., т. е. эта матрица имеет вид (Напомним, что символ ≜ означает равенство по определению)
 (1.15)
(1.15)
где 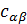 ,
,  ,…,
,…,  — произвольные постоянные.
— произвольные постоянные.
Если же  , то легко показать, что в этом случае
, то легко показать, что в этом случае
 (1.16)
(1.16)
а при 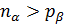
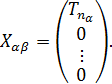 (1.17)
(1.17)
Про матрицы (1.15), (1.16) и (1.17) говорят, что они имеют правильную верхнюю треугольную форму. Число произвольных постоянных в такой матрице  равно наименьшему из чисел
равно наименьшему из чисел  и
и  . Таким образом, при решении каждого из уравнений (1.8) возможны две принципиально различные ситуации:
. Таким образом, при решении каждого из уравнений (1.8) возможны две принципиально различные ситуации:
1)  в этом случае соответствующее уравнение из системы (1.8) имеет только тривиальное решение;
в этом случае соответствующее уравнение из системы (1.8) имеет только тривиальное решение;
2)  ; в этом случае соответствующее уравнение из системы (1.8) имеет нетривиальное решение правильной верхней треугольной формы, а число произвольных параметров в решении равно наименьшему из чисел
; в этом случае соответствующее уравнение из системы (1.8) имеет нетривиальное решение правильной верхней треугольной формы, а число произвольных параметров в решении равно наименьшему из чисел  и
и  .
.
Полученный результат позволяет определить структуру каждого блока  в блочном представлении матрицы
в блочном представлении матрицы

которая является решением уравнения (1.7). У этой матрицы имеются ненулевые блоки в том и только том случае, когда матрицы (1.3), входящие в уравнение (1.7), имеют хотя бы но одному одинаковому собственному значению (не обязательно одинаковой кратности).
Чтобы получить решение исходного уравнения (1.1), следует воспользоваться формулой (1.6).
Пример 1.1. Требуется решить уравнение
 (1.18)
(1.18)
Сначала решаем характеристическое уравнение  матрицы А. В результате находим, что
матрицы А. В результате находим, что 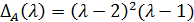 ), и, следовательно, собственные значения матрицы А таковы:
), и, следовательно, собственные значения матрицы А таковы:
 (1.19)
(1.19)
Для приведения матрицы А к канонической жордановой форме умножим ее слева на U, а справа на  , где
, где
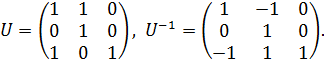 (1.20)
(1.20)
В итоге получим
 (1.21)
(1.21)
Аналогичные действия выполняем относительно матрицы В. Корнями ее характеристического уравнения являются числа
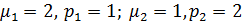 (1.22)
(1.22)
С помощью матриц
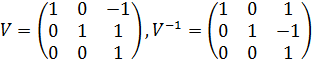 (1.23)
(1.23)
матрица В приводится к канонической жордановой форме:
 (1.24)
(1.24)
Вводя замену (см. (1.6))
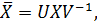 (1.25)
(1.25)
получаем уравнение
 (1.26)
(1.26)
где матрицы  и
и 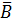 определяются формулами (1.21) и (1.24). Матрицу
определяются формулами (1.21) и (1.24). Матрицу  представляем в блочной форме
представляем в блочной форме 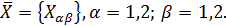
По индексу α мы перебираем собственные значения матрицы A, а по индексу β — собственные значения матрицы В. Так как собственному значению  (см. (1.19)) матрицы А соответствует кратный элементарный делитель
(см. (1.19)) матрицы А соответствует кратный элементарный делитель 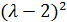 , а собственному значению
, а собственному значению 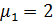 (см. (1.22)) матрицы В соответствует простой элементарный делитель
(см. (1.22)) матрицы В соответствует простой элементарный делитель 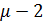 , то матрица (блок)
, то матрица (блок) 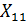 имеет размерность 2×1.
имеет размерность 2×1.
Поэтому если  представить в виде
представить в виде
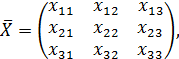
то получаем
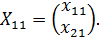
Анализируя другие пары  , аналогичными рассуждениями определим структуру остальных блоков матрицы
, аналогичными рассуждениями определим структуру остальных блоков матрицы  :
:
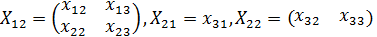
Уравнение (1.26) теперь записываем в виде
 (1.27)
(1.27)
Если же матрицы  и
и 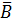 представить в блочной форме:
представить в блочной форме:

где

то уравнение (1.27) можно записать в виде

Согласно правилам перемножения блочных матриц отсюда получаем
систему матричных уравнений относительно неизвестных блоков  :
:




Решая эти уравнения, получаем

где 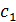 и
и  — произвольные постоянные. Следовательно,
— произвольные постоянные. Следовательно,

Чтобы получить решение исходного уравнения (1.18), следует воспользоваться формулой (1.25), согласно которой
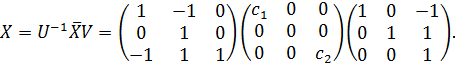
Следовательно, матрица X определяется в виде

Полученный результат, проиллюстрированный решением примера, позволяет сформулировать процедуру решения матричного уравнения (1.1).
Она состоит в следующем.
1. Найти собственные значения матриц А и В.
2. Построить все элементарные делители этих матриц.
3. Построить матрицы U и V, с помощью которых матрицы A и В приводятся к канонической жордановой форме  и
и 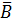 (см. (1.2)).
(см. (1.2)).
4. В уравнении (1.1) сделать замену X на  по формуле (1.6), в результате чего уравнение (1.1) приведется к виду (1.7). Здесь матрицы
по формуле (1.6), в результате чего уравнение (1.1) приведется к виду (1.7). Здесь матрицы  и
и 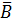 имеют жорданову форму и, следовательно, имеют блочную структуру (см. (1.3))
имеют жорданову форму и, следовательно, имеют блочную структуру (см. (1.3))
 ,
, 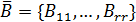 . (1.28)
. (1.28)
5. Матрицу  представить в блочной форме
представить в блочной форме
 (1.29)
(1.29)
где размерности матриц  определяются соответствующими блоками матриц
определяются соответствующими блоками матриц 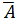 и
и 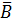 (см. (1.28)). В частности, число строк матрицы
(см. (1.28)). В частности, число строк матрицы 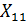 равно порядку матрицы
равно порядку матрицы  , а число ее столбцов равно порядку матрицы
, а число ее столбцов равно порядку матрицы 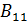 .
.
6. Подставить матрицы (1.28) и (1.29) в уравнение (1.7) и получить систему независимых уравнений относительно блоков  . Решить эту систему, в результате чего будет найдена матрица (1.29).
. Решить эту систему, в результате чего будет найдена матрица (1.29).
7. С помощью преобразования (1.6) найти искомое решение X.
Замечание 1.1. Если матрицы А и В не имеют общих характеристических чисел (т. е. характеристические полиномы  и
и  взаимно просты), то уравнение (1.1) имеет только тривиальное решение.
взаимно просты), то уравнение (1.1) имеет только тривиальное решение.
1.2. Решение линейного неоднородного уравнения. Будем рассматривать уравнение
 (1.38)
(1.38)
Оно эквивалентно системе скалярных уравнений

Однако мы не будем использовать традиционные методы ее решения, основанные на представлении системы в виде  . Для нас важно установить явную зависимость решения от матриц А и В.
. Для нас важно установить явную зависимость решения от матриц А и В.
Будем предполагать, что матрицы А, B и F вещественны. Соответствующая однородная система уравнений может быть представлена в виде
 (1.39)
(1.39)
и вопрос о ее разрешимости, а также о практическом способе построения общего решения уравнения (1.39) рассмотрен в п. 1. Там было установлено, что это уравнение имеет только нулевое решение в том и только том случае, когда матрицы А и В не имеют общих характеристических чисел.
Отсюда можно сделать важный
В ы вод. Если матрицы А и В не имеют общих характеристических чисел, то уравнение (1.38) имеет единственное решение. Если же у них есть общие характеристические числа, то в зависимости от свободного члена F возможны два случая: либо уравнение (1.38) противоречиво, либо оно имеет бесчисленное множество решений, определяемых формулой  , где
, где  общее решение однородного уравнения (1.39), а
общее решение однородного уравнения (1.39), а 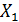 — некоторое частное решение уравнения (1.38).
— некоторое частное решение уравнения (1.38).
Что касается процедуры практического решения уравнения (1.38), то она полностью совпадает с той, которая использовалась при решении однородного уравнения (1.39).
1.3. Скалярное уравнение. Рассмотрим уравнение
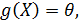 (1.40)
(1.40)
где
 (1.41)
(1.41)
- заданный многочлен переменной  .
.
Требуется решить это уравнение.
Для каждого решения 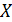 полином
полином 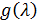 является аннулирующим и поэтому делится без остатка на минимальный многочлен матрицы X. Если n - порядок матрицы X, то в качестве
является аннулирующим и поэтому делится без остатка на минимальный многочлен матрицы X. Если n - порядок матрицы X, то в качестве  может быть взят любой из полиномов, начиная с
может быть взят любой из полиномов, начиная с 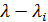 и кончая полиномом типа (1.41) (с теми же корнями), степень которого равна n.
и кончая полиномом типа (1.41) (с теми же корнями), степень которого равна n.
Поэтому каждый из них можно представить в виде
 (1.42)
(1.42)
где
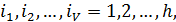
 (1.43)
(1.43)
Причем среди индексов 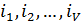 могут быть и равные.
могут быть и равные.
Отсюда следует, что искомая матрица представима в виде
 (1.44)
(1.44)
где Т — произвольная неособенная матрица. Следовательно, решение представляет собой многопараметрическое семейство, которое распадается на конечное число классов подобных матриц, определяемых формулой (1.44).
Замечательным примером, иллюстрирующим все многообразие возможных ситуаций при решении скалярных уравнений, является квадратное уравнение, анализ которого представляет не только теоретический интерес.
Пример 1.3. Дано уравнение
 (1.45)
(1.45)
Матрица, которая удовлетворяет этому уравнению, называется идемпотентной. Элементарными делителями идемпотентной матрицы могут быть только 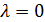 и
и 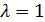 (см. (1.41)). Поэтому идемпотентную матрицу можно определить как матрицу простой структуры (т. е. приводящейся к диагональной форме) с характеристическими числами, равными нулю или единице. Формула, охватывающая все идемпотентные матрицы данного порядка, имеет вид
(см. (1.41)). Поэтому идемпотентную матрицу можно определить как матрицу простой структуры (т. е. приводящейся к диагональной форме) с характеристическими числами, равными нулю или единице. Формула, охватывающая все идемпотентные матрицы данного порядка, имеет вид 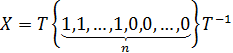 , где Т - произвольная матрица порядка n.Эти матрицы распадаются на классы эквивалентных между собой матриц.
, где Т - произвольная матрица порядка n.Эти матрицы распадаются на классы эквивалентных между собой матриц.
К первому классу относятся матрицы  . Во второй
. Во второй
класс входят матрицы вида  и т. д.
и т. д.
Рассмотрим теперь более общее уравнение  , где
, где  — регулярная функция в некоторой области G комплексного аргумента. От каждого решения X потребуется, чтобы все его характеристические числа лежали в области G.
— регулярная функция в некоторой области G комплексного аргумента. От каждого решения X потребуется, чтобы все его характеристические числа лежали в области G.
Пусть  все нули функции
все нули функции 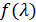 ,a
,a 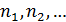 ,— соответствующие
,— соответствующие
им кратности. Как и в предыдущем случае, каждый элементарный делитель матрицы X должен иметь вид  ,
,  . Поэтому решениями будут матрицы
. Поэтому решениями будут матрицы

 (2.1)
(2.1)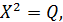 (2.2)
(2.2) .
. , где
, где  , а
, а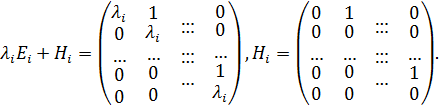
 , матрицы Q отличны от нуля.
, матрицы Q отличны от нуля. . Будем рассматривать уравнение
. Будем рассматривать уравнение , (1.1)
, (1.1)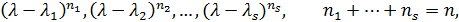

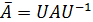 ,
, 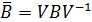 , (1.2)
, (1.2)
 (1.3)
(1.3)  — единичная матрица порядка q,
— единичная матрица порядка q,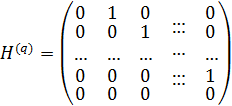 . (1.4)
. (1.4)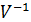 . Тогда получим
. Тогда получим 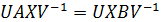 . Очевидно, что это уравнение можно переписать в виде
. Очевидно, что это уравнение можно переписать в виде (1.5)
(1.5)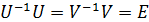 .
.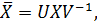 (1.6)
(1.6)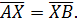 (1.7)
(1.7) разобьем на блоки
разобьем на блоки 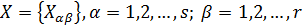 , каждый из которых является прямоугольным, но они построены так, чтобы матрица
, каждый из которых является прямоугольным, но они построены так, чтобы матрица  имела размерность
имела размерность  (
( - число строк,
- число строк,  - число столбцов).
- число столбцов).
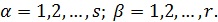
 (1.8)
(1.8) (1.9)
(1.9)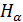 имеет порядок
имеет порядок  равен
равен 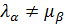 . Обе части выбранного уравнения из (1.8) умножим на
. Обе части выбранного уравнения из (1.8) умножим на  , а затем в полученном уравнении заменяем
, а затем в полученном уравнении заменяем  на
на 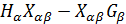 . Эту операцию повторим q — 1 раз. В итоге получим уравнение
. Эту операцию повторим q — 1 раз. В итоге получим уравнение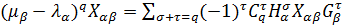 (1.10)
(1.10)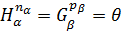 . (1.11)
. (1.11) , то в каждом члене суммы,
, то в каждом члене суммы,  ,
,  . В силу равенств (1.11) либо
. В силу равенств (1.11) либо  , либо
, либо  . Так как, кроме того, в рассматриваемом случае
. Так как, кроме того, в рассматриваемом случае  (1.12)
(1.12) . В этом случае соответствующее уравнение из системы (1.8) принимает вид
. В этом случае соответствующее уравнение из системы (1.8) принимает вид (1.13)
(1.13)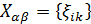 ,
,  . Тогда уравнение (1.13) можно заменить эквивалентной ему системой уравнений
. Тогда уравнение (1.13) можно заменить эквивалентной ему системой уравнений
 (1.14)
(1.14)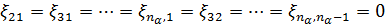 .
. . Из свойств 1) и 2) следует, что матрица
. Из свойств 1) и 2) следует, что матрица 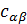 . Элементы на линии над главной диагональю равны другому постоянному числу
. Элементы на линии над главной диагональю равны другому постоянному числу  и т. д., т. е. эта матрица имеет вид (Напомним, что символ ≜ означает равенство по определению)
и т. д., т. е. эта матрица имеет вид (Напомним, что символ ≜ означает равенство по определению) (1.15)
(1.15) — произвольные постоянные.
— произвольные постоянные. , то легко показать, что в этом случае
, то легко показать, что в этом случае (1.16)
(1.16)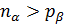
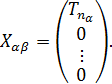 (1.17)
(1.17) в этом случае соответствующее уравнение из системы (1.8) имеет только тривиальное решение;
в этом случае соответствующее уравнение из системы (1.8) имеет только тривиальное решение;
 (1.18)
(1.18) матрицы А. В результате находим, что
матрицы А. В результате находим, что 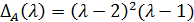 ), и, следовательно, собственные значения матрицы А таковы:
), и, следовательно, собственные значения матрицы А таковы: (1.19)
(1.19) , где
, где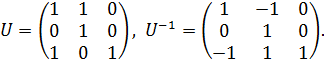 (1.20)
(1.20) (1.21)
(1.21)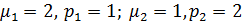 (1.22)
(1.22)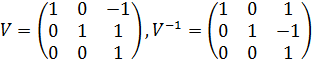 (1.23)
(1.23) (1.24)
(1.24) (1.26)
(1.26) и
и 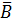 определяются формулами (1.21) и (1.24). Матрицу
определяются формулами (1.21) и (1.24). Матрицу 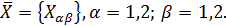
 (см. (1.19)) матрицы А соответствует кратный элементарный делитель
(см. (1.19)) матрицы А соответствует кратный элементарный делитель 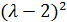 , а собственному значению
, а собственному значению 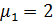 (см. (1.22)) матрицы В соответствует простой элементарный делитель
(см. (1.22)) матрицы В соответствует простой элементарный делитель 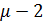 , то матрица (блок)
, то матрица (блок) 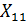 имеет размерность 2×1.
имеет размерность 2×1.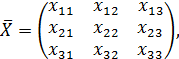
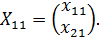
 , аналогичными рассуждениями определим структуру остальных блоков матрицы
, аналогичными рассуждениями определим структуру остальных блоков матрицы 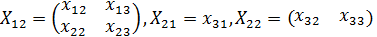
 (1.27)
(1.27)


 :
:




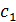 и
и  — произвольные постоянные. Следовательно,
— произвольные постоянные. Следовательно,
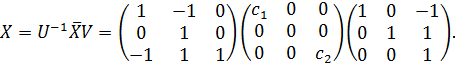

 ,
, 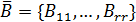 . (1.28)
. (1.28) (1.29)
(1.29)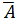 и
и  , а число ее столбцов равно порядку матрицы
, а число ее столбцов равно порядку матрицы 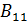 .
. и
и  взаимно просты), то уравнение (1.1) имеет только тривиальное решение.
взаимно просты), то уравнение (1.1) имеет только тривиальное решение. (1.38)
(1.38)
 . Для нас важно установить явную зависимость решения от матриц А и В.
. Для нас важно установить явную зависимость решения от матриц А и В. (1.39)
(1.39) , где
, где  общее решение однородного уравнения (1.39), а
общее решение однородного уравнения (1.39), а 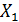 — некоторое частное решение уравнения (1.38).
— некоторое частное решение уравнения (1.38).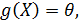 (1.40)
(1.40) (1.41)
(1.41) .
.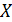 полином
полином 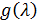 является аннулирующим и поэтому делится без остатка на минимальный многочлен матрицы X. Если n - порядок матрицы X, то в качестве
является аннулирующим и поэтому делится без остатка на минимальный многочлен матрицы X. Если n - порядок матрицы X, то в качестве  может быть взят любой из полиномов, начиная с
может быть взят любой из полиномов, начиная с 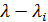 и кончая полиномом типа (1.41) (с теми же корнями), степень которого равна n.
и кончая полиномом типа (1.41) (с теми же корнями), степень которого равна n. (1.42)
(1.42)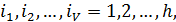
 (1.43)
(1.43)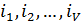 могут быть и равные.
могут быть и равные. (1.44)
(1.44) (1.45)
(1.45)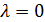 и
и 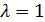 (см. (1.41)). Поэтому идемпотентную матрицу можно определить как матрицу простой структуры (т. е. приводящейся к диагональной форме) с характеристическими числами, равными нулю или единице. Формула, охватывающая все идемпотентные матрицы данного порядка, имеет вид
(см. (1.41)). Поэтому идемпотентную матрицу можно определить как матрицу простой структуры (т. е. приводящейся к диагональной форме) с характеристическими числами, равными нулю или единице. Формула, охватывающая все идемпотентные матрицы данного порядка, имеет вид 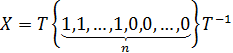 , где Т - произвольная матрица порядка n.Эти матрицы распадаются на классы эквивалентных между собой матриц.
, где Т - произвольная матрица порядка n.Эти матрицы распадаются на классы эквивалентных между собой матриц. . Во второй
. Во второй и т. д.
и т. д. , где
, где  — регулярная функция в некоторой области G комплексного аргумента. От каждого решения X потребуется, чтобы все его характеристические числа лежали в области G.
— регулярная функция в некоторой области G комплексного аргумента. От каждого решения X потребуется, чтобы все его характеристические числа лежали в области G. все нули функции
все нули функции 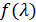 ,a
,a 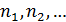 ,— соответствующие
,— соответствующие ,
,  . Поэтому решениями будут матрицы
. Поэтому решениями будут матрицы