Аналогичны формулы для определения ускорения точки:
 Формулы определяют величину и направление вектора ускорения. В формулах (1.6) и (1.8) приведены используемые в различных учебниках обозначения проекций скоростей и ускорений точек на оси декартовой системы координат.
Формулы определяют величину и направление вектора ускорения. В формулах (1.6) и (1.8) приведены используемые в различных учебниках обозначения проекций скоростей и ускорений точек на оси декартовой системы координат.
24.Определение ускорения точки при задании ее движения естественным способом. Ускорение определяется как производная от вектора скорости:
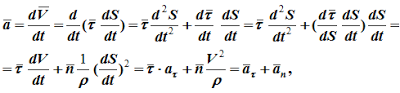 т.е. a=aτ+an.
т.е. a=aτ+an.  aτ=τ⋅dV/dt=τ⋅d2S/dt2, aτ=dV/dt=τ⋅d2S/dt2- касательное ускорение; оно характеризует быстроту изменения величины скорости точки; an=n⋅V2/ρ, an=V2/ρ - нормальное ускорение точки; характеризует быстроту изменения направления вектора скорости; ρ - радиус кривизны траектории в данной точке (например, для окружности: ρ=R, для прямой линии ρ=∞).Полное ускорение точки определяется следующим образом
aτ=τ⋅dV/dt=τ⋅d2S/dt2, aτ=dV/dt=τ⋅d2S/dt2- касательное ускорение; оно характеризует быстроту изменения величины скорости точки; an=n⋅V2/ρ, an=V2/ρ - нормальное ускорение точки; характеризует быстроту изменения направления вектора скорости; ρ - радиус кривизны траектории в данной точке (например, для окружности: ρ=R, для прямой линии ρ=∞).Полное ускорение точки определяется следующим образом
 Выше отмечалось, что всегда можно перейти от одного способа задания закона движения точки к другому. Поэтому, преобразовывая одни и те же формулы, можно получить другое их написание.
Выше отмечалось, что всегда можно перейти от одного способа задания закона движения точки к другому. Поэтому, преобразовывая одни и те же формулы, можно получить другое их написание.
25.Поступательное движение твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему начальному положению. Примеры поступательного движения: движение педалей велосипеда относительно его рамы, движение поршней в цилиндрах двигателя внутреннего сгорания относительно цилиндров, движение кабин колеса обозрения относительно Земли. Теорема. При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы.
26.Вращательное движение твердого тела – это движение твердого тела, имеющего как минимум две неподвижные точки. Прямая, проходящая через эти точки, называется осью вращения.
Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения. Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:
 В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернется на угол 2π⋅ n, где n – число оборотов в минуту (об/мин). Разделив этот угол на число секунд в минуте, получим
В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернется на угол 2π⋅ n, где n – число оборотов в минуту (об/мин). Разделив этот угол на число секунд в минуте, получим
 Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости
Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости
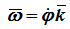 где k – единичный вектор оси вращения. Угловое ускорение – мера изменения угловой скорости:
где k – единичный вектор оси вращения. Угловое ускорение – мера изменения угловой скорости:
 Вектор углового ускорения – производная вектора угловой скорости по времени (рис. 1.4)
Вектор углового ускорения – производная вектора угловой скорости по времени (рис. 1.4)
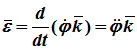
27.Угловая скорость и угловое ускорение. Угловой скоростью называют векторную величину, характеризующую быстроту вращения твердого тела, определяемую как приращение угла поворота тела за промежуток времени. Угловая скорость является векторной величиной. Угловым ускорением называют степень изменения угловой скорости. 
28.Скорость и ускорение точек вращающегося тела. При вращении твердого тела вокруг неподвижной оси каждая точка тела движется по окружности. Радиус окружности равен расстоянию от точки до оси вращения. Закон движения точки может быть задан естественным способом. Длина дуги (дуговая координата) определяется по формуле
 Скорость точки V=dS/dt=dφ⋅R/dt=ωR. Скорость направлена по касательной к траектории, поэтому можно написать
Скорость точки V=dS/dt=dφ⋅R/dt=ωR. Скорость направлена по касательной к траектории, поэтому можно написать
 Вектор скорости можно получить векторным произведением: V=ω⊗ r, V=ω⋅rsinα=ωR.Ускорение при естественном способе задания движения определяется как сумма касательного и нормального ускорений
Вектор скорости можно получить векторным произведением: V=ω⊗ r, V=ω⋅rsinα=ωR.Ускорение при естественном способе задания движения определяется как сумма касательного и нормального ускорений
29.Сложное движение. Основные понятия. При решении многих инженерных задач приходится рассматривать движение точки по отношению к некоторому твердому телу, которое в свою очередь движется. При математическом описании такого сложного движения вводится неподвижная система отсчета и система отсчета жестко связанная с движущимся твердым телом, т.е. подвижная система отсчета. Тогда движение точки относительно подвижной системы отсчета называется относительным движением. Движение твердого тела и неизменно связанной с ним подвижной системы отсчета относительно неподвижной системы называется переносным движением, а движение точки относительно неподвижной системы – абсолютным движением. Переносной скоростью и переносным ускорением называется скорость и ускорение той точки твердого тела или подвижной системы отсчета, в которой в данный момент находится движущаяся точка.
30.Сложение скоростей — с помощью данного закона определяется скорость движения тела относительно неподвижной системы отсчёта. Она равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной системы
 Для того, чтоб было более понятно, как работает закон сложения скоростей, рассмотрим такой пример. Вагон движется со скоростью 50 км\ч (это будет
Для того, чтоб было более понятно, как работает закон сложения скоростей, рассмотрим такой пример. Вагон движется со скоростью 50 км\ч (это будет  ), в вагоне идет человек со скоростью 3 км\ч (это будет
), в вагоне идет человек со скоростью 3 км\ч (это будет  ), найти скорость человека относительно Земли.
), найти скорость человека относительно Земли.
У данной задачи будет два решения. Если человек будет идти по направлению движения вагона, то скорость человека относительно Земли будет 53 км\ч.
 А если человек будет идти против движения вагона, то скорость человека относительно Земли будет 47 км\ч.
А если человек будет идти против движения вагона, то скорость человека относительно Земли будет 47 км\ч. 
 — Конечная скорость тела
— Конечная скорость тела
 — Скорость тел в различных инерциальных системах отчета
— Скорость тел в различных инерциальных системах отчета
31.Сложение ускорений точки в общем случае переносного движения (теорема Кориолиса). Сложным называется движение точки (или тела), которое рассматривается одновременно в разных системах отсчета. Теорема о сложении скоростей. При сложном движении точки абсолютная скорость равна  сумме ее относительной
сумме ее относительной  и переносной
и переносной  скоростей:
скоростей:  . Теорема о сложении ускорений (теорема Кориолиса). При непоступательном переносном движении абсолютное ускорение точки
. Теорема о сложении ускорений (теорема Кориолиса). При непоступательном переносном движении абсолютное ускорение точки 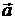 находится как сумма трех ускорений: относительного
находится как сумма трех ускорений: относительного  , переносного
, переносного 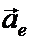 и ускорения Кориолиса
и ускорения Кориолиса 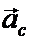
 ,
,  ,где
,где  − угловая скорость переносного вращения. νr - относительная скорость точки.
− угловая скорость переносного вращения. νr - относительная скорость точки.
32.Ускорение Кориолиса или поворотное ускорение определяется по формуле аC = 2 ωe * νr, где ωe - переносная угловая скорость, νr - относительная скорость точки. Направление ускорения Кориолиса определяется по правилу векторного произведения или по правилу Жуковского.Величина ускорения Кориолиса определяется выражением, aC = 2 ωe νr sinα,где α – угол между векторами ωe и νr.
33.Понятие плоского движения твердого тела. Плоским движением твердого тела называют такое его движение, при котором каждая его точка все время движется в одной и той же неподвижной плоскости. Часто это движение называют плоскопараллельным, так как плоскости, в которых движутся отдельные точки, параллельны между собой. Траектории точек тела при плоском движении являются плоскими кривыми. Такой случай движения часто реализуется в технике при движении механизмов и машин. Вращательное движение твердого тела вокруг неподвижной оси является частным случаем плоского движения.
34.Уравнения движения плоской фигуры: 1.Уравнение движения центра масс, определяющее скорость поступательного движения тела массой т: mdvc/dt=(сумм)i Fi, где vc – скорость центра масс тела; (сумм)i Fi – сумма всех внешних сил.
2. Уравнение динамики плоского движения относительно оси, проходящей через центр масс тела и неподвижной относительно тела, определяющее угловую скорость wc вращательного движения: Icdwc/dt=внешн.Mc, где Ic и внешн.Mc – момент инерции тела и момент внешних сил относительно этой оси соответственно. Кинетическая энергия тела, совершающего плоское движение. Если рассматривать движение тела как вращение вокруг мгновенной оси, то элемент массы mi имеет в данный момент времени линейную скорость vi = wri, где ri – расстояние от этого элемента до мгновенной оси. Кинетическая энергия отдельного элемента тела будет:Eki=miv2i=mir2iw2, а кинетическая энергия всего тела: Ek=(сумм) Eki=w2/2(сумм) mir2i=Iw2/2, где I – момент инерции тела относительно мгновенной оси. Теорема Кёнига: полная кинетическая энергия при плоском движении твердого тела равна сумме кинетических энергий поступательного и вращательного движений (вращение рассматривается вокруг оси, проходящей через центр масс).
35.Скорости точек тела при плоском движении. Скорость любой точки плоской фигуры равна геометрической сумме скорости выбранного полюса и скорости точки во вращательном движении фигуры вокруг полюса.
 Производная от вектора AM, постоянного по величине и переменного по направлению, численно равна скорости точки М при вращении ее вокруг точки А.
Производная от вектора AM, постоянного по величине и переменного по направлению, численно равна скорости точки М при вращении ее вокруг точки А.
36.Ускорения точек тела при плоском движении. Теорема об ускорении точек в плоскопараллельном движении: Из выражения VM=VA+VMA (или VM=VA + ω ⋅ AM) путем дифференцирования получаем
 aврMA= ε ⋅ AM - вращательное ускорение точки М при вращении вокруг точки А.
aврMA= ε ⋅ AM - вращательное ускорение точки М при вращении вокруг точки А.
 aцMA= ω2 ⋅ AM - центростремительное ускорение точки М при вращении вокруг точки А. Центростремительное ускорение a-цMA направлено от точки М к полюсу А.
aцMA= ω2 ⋅ AM - центростремительное ускорение точки М при вращении вокруг точки А. Центростремительное ускорение a-цMA направлено от точки М к полюсу А. 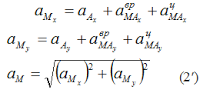
37.Мгновенный центр скоростей (МЦС). Теорема Эйлера- Шаля доказывает, что любое непоступательное перемещение фигуры в плоскости можно осуществить поворотом вокруг некоторого неподвижного центра. В соответствии с этим легко доказывается, что при плоско-параллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нулю. Эту точку называют мгновенным центром скоростей (МЦС). При определении положения МЦС скорость любой точки может быть записана: VM=VCV+VMCV, где точка СV выбрана за полюс. Поскольку это МЦС и VCV=0, то скорость любой точки определяется как скорость вращении вокруг мгновенного центра скоростей.
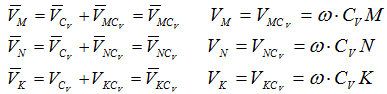
38.Основные аксиомы классической механики. Первая аксиома или закон инерции. Существуют инерциальные системы отсчета, относительно которых материальная точка, не испытывающая действия или находящаяся под действием уравновешенной системы сил, сохраняет состояние покоя или равномерного прямолинейного движения. Вторая аксиома. Ускорение точки прямо пропорционально силе и направленно в сторону этой силы. Масса- мера инертности точки.
Третья аксиома. Всякому действию есть противодействие, равное по величине и противоположное по направлению.
Четвертая аксиома. Закон независимости действия сил. Если к точке приложена система сил, то ускорение точки равно векторной сумме ускорений, получаемых от каждой силы в отдельности.

39.  Дифференциальные уравнения движения материальной точки. Уравнение (1), (2) являются дифференциальными уравнениями материальной точки в векторной форме. Спроектировав оба равенства (1) на оси координат:
Дифференциальные уравнения движения материальной точки. Уравнение (1), (2) являются дифференциальными уравнениями материальной точки в векторной форме. Спроектировав оба равенства (1) на оси координат:

 Пусть траектория движения точки известна
Пусть траектория движения точки известна
 Если траектория точки известна, всегда можно построить естественные оси траектории.
Если траектория точки известна, всегда можно построить естественные оси траектории.




Центр масс
Центром масс механической системы называется такая геометрическая точка C, сконцентрируя в которой массу M всей механической системы, получим, что ее статический момент массы равен статическому моменту массы всей механической системы, т.е.
41.Моменты инерции МОМЕНТОМ ИНЕРЦИИ I тела относительно точки, оси или плоскости называется сумма произведений массы точек тела mi, на квадраты их расстояний ri до точки, оси или плоскости:
 Момент инерции тела относительно оси является мерой инерции тела во вращательном движении вокруг этой оси.Момент инерции тела может быть также выражен через массу М тела и его радиус инерции r:
Момент инерции тела относительно оси является мерой инерции тела во вращательном движении вокруг этой оси.Момент инерции тела может быть также выражен через массу М тела и его радиус инерции r:
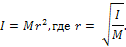 МОМЕНТЫ ИНЕРЦИИ ОТНОСИТЕЛЬНО ОСЕЙ, ПЛОСКОСТЕЙ И НАЧАЛА ДЕКАРТОВЫХ КООРДИНАТ. Осевые моменты инерции:
МОМЕНТЫ ИНЕРЦИИ ОТНОСИТЕЛЬНО ОСЕЙ, ПЛОСКОСТЕЙ И НАЧАЛА ДЕКАРТОВЫХ КООРДИНАТ. Осевые моменты инерции:
 Моменты инерции относительно плоскостей координат:
Моменты инерции относительно плоскостей координат:

Момент инерции относительно начала координат (полярный момент инерции):

Центробежные моменты инерции

СВЯЗЬ МЕЖДУ ОСЕВЫМИ, ПЛОСКОСТНЫМИ И ПОЛЯРНЫМ МОМЕНТАМИ ИНЕРЦИИ:

ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПЕРЕМЕНЕ ОСЕЙ. Момент инерции Iu1 относительно оси u1, параллельной данной оси u:

где Iu - момент инерции тела относительно оси u; l(l1) - расстояние от оси u (от оси u1) до параллельной им оси uс, проходящей через центр масс тела; а - расстояние между осями u и u1.
ИЗМЕНЕНИЕ ЦЕНТРОБЕЖНЫХ МОМЕНТОВ ИНЕРЦИИ ПРИ ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ ОСЕЙ:  где
где  - центробежный момент инерции относительно центральных осей хс, yс, параллельных осям х, у; М - масса тела; xс, yс - координаты центра масс в системе осей х, у. ИЗМЕНЕНИЕ ЦЕНТРОБЕЖНОГО МОМЕНТА ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ x, y ВОКРУГ ОСИ z НА УГОЛ α В ПОЛОЖЕНИЕ x1y1 (рис. 3):
- центробежный момент инерции относительно центральных осей хс, yс, параллельных осям х, у; М - масса тела; xс, yс - координаты центра масс в системе осей х, у. ИЗМЕНЕНИЕ ЦЕНТРОБЕЖНОГО МОМЕНТА ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ x, y ВОКРУГ ОСИ z НА УГОЛ α В ПОЛОЖЕНИЕ x1y1 (рис. 3):

42.Дифференциальные уравнения движения системы. Пусть имеется система, состоящая из n – точек.
 В проекциях на декартовые оси:
В проекциях на декартовые оси:
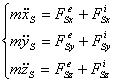 Суммарными характеристиками меры механического движения является: 1) количество движения системы, 2) момент количества движения, 3) кинетическая энергия системы. Две первые меры являются векторными, а последняя – скалярной.
Суммарными характеристиками меры механического движения является: 1) количество движения системы, 2) момент количества движения, 3) кинетическая энергия системы. Две первые меры являются векторными, а последняя – скалярной.
43.Количество движения точки. Элементарный и полный импульсы силы. Количеством движенияматериальной точки  называют вектор, равный произведению массы точки на ее скорость, т.е.
называют вектор, равный произведению массы точки на ее скорость, т.е.

Количеством движения системы  называют векторную сумму количеств движения отдельных точек системы, т.е.
называют векторную сумму количеств движения отдельных точек системы, т.е.
 Количество движения системы можно выразить через массу системы и скорость центра масс если масса системы не изменяется при движении.
Количество движения системы можно выразить через массу системы и скорость центра масс если масса системы не изменяется при движении.
 Действие силы
Действие силы  на материальную точку в течении времени
на материальную точку в течении времени 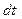 можно охарактеризовать элементарным импульсом силы
можно охарактеризовать элементарным импульсом силы  .Полный импульс силы
.Полный импульс силы 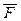 за время
за время  , или импульс силы
, или импульс силы  , определяется по формуле
, определяется по формуле  . Если сила
. Если сила 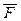 постоянна и по величине, и по направлению (
постоянна и по величине, и по направлению ( ),
),  .
.
Единицей измерения импульса в СИ является – 
44.Теорема об изменении количества движения точки. Действие силы  на материальную точку в течение времени dt можно охарактеризовать так называемым элементарным импульсом силы
на материальную точку в течение времени dt можно охарактеризовать так называемым элементарным импульсом силы  . Полный импульс силы за время t, или импульс силы определяют по формуле
. Полный импульс силы за время t, или импульс силы определяют по формуле
 Дифференциальное уравнение движения материальной точки под действием силы
Дифференциальное уравнение движения материальной точки под действием силы  можно представить в следующей векторной форме:
можно представить в следующей векторной форме:
 Так как масса точки считается постоянной, то ее можно внести под знак производной. Тогда
Так как масса точки считается постоянной, то ее можно внести под знак производной. Тогда
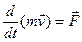 Эта формула выражает теорему об изменении количества движения точки в дифференциальной форме: первая производная по времени от количества движения точки равна действующей на точку силе. (Причиной изменения количества движения точки является сила).В проекциях на оси координат теорема записывается следующим образом:
Эта формула выражает теорему об изменении количества движения точки в дифференциальной форме: первая производная по времени от количества движения точки равна действующей на точку силе. (Причиной изменения количества движения точки является сила).В проекциях на оси координат теорема записывается следующим образом:
 Если обе части теоремы умножить на dt, то получим другую форму этой же теоремы
Если обе части теоремы умножить на dt, то получим другую форму этой же теоремы
 .т.е. дифференциал от количества движения точки равен элементарному импульсу силы, действующей на точку.Интегрируя обе части в пределах от нуля до t, имеем:
.т.е. дифференциал от количества движения точки равен элементарному импульсу силы, действующей на точку.Интегрируя обе части в пределах от нуля до t, имеем:
 .где
.где  -скорость точки в момент t,
-скорость точки в момент t,  -скорость при t=0,
-скорость при t=0,  -импульс силы за время t.Это выражение часто называют теоремой импульсов в конечной (или интегральной) форме: изменение количества движения точки за какой-либо промежуток времени равно импульсу силы за тот же промежуток времени.Для материальной точки теорема об изменении количества движения в любой из форм, по существу, не отличается от дифференциальных уравнений движения точки.
-импульс силы за время t.Это выражение часто называют теоремой импульсов в конечной (или интегральной) форме: изменение количества движения точки за какой-либо промежуток времени равно импульсу силы за тот же промежуток времени.Для материальной точки теорема об изменении количества движения в любой из форм, по существу, не отличается от дифференциальных уравнений движения точки.



 Формулы определяют величину и направление вектора ускорения. В формулах (1.6) и (1.8) приведены используемые в различных учебниках обозначения проекций скоростей и ускорений точек на оси декартовой системы координат.
Формулы определяют величину и направление вектора ускорения. В формулах (1.6) и (1.8) приведены используемые в различных учебниках обозначения проекций скоростей и ускорений точек на оси декартовой системы координат.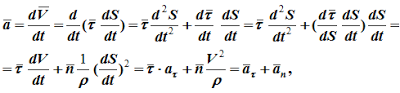 т.е. a=aτ+an.
т.е. a=aτ+an.  aτ=τ⋅dV/dt=τ⋅d2S/dt2, aτ=dV/dt=τ⋅d2S/dt2- касательное ускорение; оно характеризует быстроту изменения величины скорости точки; an=n⋅V2/ρ, an=V2/ρ - нормальное ускорение точки; характеризует быстроту изменения направления вектора скорости; ρ - радиус кривизны траектории в данной точке (например, для окружности: ρ=R, для прямой линии ρ=∞).Полное ускорение точки определяется следующим образом
aτ=τ⋅dV/dt=τ⋅d2S/dt2, aτ=dV/dt=τ⋅d2S/dt2- касательное ускорение; оно характеризует быстроту изменения величины скорости точки; an=n⋅V2/ρ, an=V2/ρ - нормальное ускорение точки; характеризует быстроту изменения направления вектора скорости; ρ - радиус кривизны траектории в данной точке (например, для окружности: ρ=R, для прямой линии ρ=∞).Полное ускорение точки определяется следующим образом Выше отмечалось, что всегда можно перейти от одного способа задания закона движения точки к другому. Поэтому, преобразовывая одни и те же формулы, можно получить другое их написание.
Выше отмечалось, что всегда можно перейти от одного способа задания закона движения точки к другому. Поэтому, преобразовывая одни и те же формулы, можно получить другое их написание. В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернется на угол 2π⋅ n, где n – число оборотов в минуту (об/мин). Разделив этот угол на число секунд в минуте, получим
В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернется на угол 2π⋅ n, где n – число оборотов в минуту (об/мин). Разделив этот угол на число секунд в минуте, получим Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости
Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости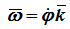 где k – единичный вектор оси вращения. Угловое ускорение – мера изменения угловой скорости:
где k – единичный вектор оси вращения. Угловое ускорение – мера изменения угловой скорости: Вектор углового ускорения – производная вектора угловой скорости по времени (рис. 1.4)
Вектор углового ускорения – производная вектора угловой скорости по времени (рис. 1.4)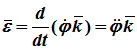

 Скорость точки V=dS/dt=dφ⋅R/dt=ωR. Скорость направлена по касательной к траектории, поэтому можно написать
Скорость точки V=dS/dt=dφ⋅R/dt=ωR. Скорость направлена по касательной к траектории, поэтому можно написать Вектор скорости можно получить векторным произведением: V=ω⊗ r, V=ω⋅rsinα=ωR.Ускорение при естественном способе задания движения определяется как сумма касательного и нормального ускорений
Вектор скорости можно получить векторным произведением: V=ω⊗ r, V=ω⋅rsinα=ωR.Ускорение при естественном способе задания движения определяется как сумма касательного и нормального ускорений Для того, чтоб было более понятно, как работает закон сложения скоростей, рассмотрим такой пример. Вагон движется со скоростью 50 км\ч (это будет
Для того, чтоб было более понятно, как работает закон сложения скоростей, рассмотрим такой пример. Вагон движется со скоростью 50 км\ч (это будет  ), в вагоне идет человек со скоростью 3 км\ч (это будет
), в вагоне идет человек со скоростью 3 км\ч (это будет  ), найти скорость человека относительно Земли.
), найти скорость человека относительно Земли. А если человек будет идти против движения вагона, то скорость человека относительно Земли будет 47 км\ч.
А если человек будет идти против движения вагона, то скорость человека относительно Земли будет 47 км\ч. 
 — Конечная скорость тела
— Конечная скорость тела — Скорость тел в различных инерциальных системах отчета
— Скорость тел в различных инерциальных системах отчета сумме ее относительной
сумме ее относительной  и переносной
и переносной  скоростей:
скоростей:  . Теорема о сложении ускорений (теорема Кориолиса). При непоступательном переносном движении абсолютное ускорение точки
. Теорема о сложении ускорений (теорема Кориолиса). При непоступательном переносном движении абсолютное ускорение точки 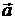 находится как сумма трех ускорений: относительного
находится как сумма трех ускорений: относительного  , переносного
, переносного 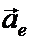 и ускорения Кориолиса
и ускорения Кориолиса 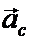
 ,
,  ,где
,где  − угловая скорость переносного вращения. νr - относительная скорость точки.
− угловая скорость переносного вращения. νr - относительная скорость точки. Производная от вектора AM, постоянного по величине и переменного по направлению, численно равна скорости точки М при вращении ее вокруг точки А.
Производная от вектора AM, постоянного по величине и переменного по направлению, численно равна скорости точки М при вращении ее вокруг точки А. aврMA= ε ⋅ AM - вращательное ускорение точки М при вращении вокруг точки А.
aврMA= ε ⋅ AM - вращательное ускорение точки М при вращении вокруг точки А. aцMA= ω2 ⋅ AM - центростремительное ускорение точки М при вращении вокруг точки А. Центростремительное ускорение a-цMA направлено от точки М к полюсу А.
aцMA= ω2 ⋅ AM - центростремительное ускорение точки М при вращении вокруг точки А. Центростремительное ускорение a-цMA направлено от точки М к полюсу А. 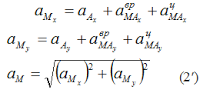
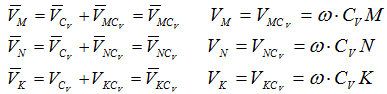

 Дифференциальные уравнения движения материальной точки. Уравнение (1), (2) являются дифференциальными уравнениями материальной точки в векторной форме. Спроектировав оба равенства (1) на оси координат:
Дифференциальные уравнения движения материальной точки. Уравнение (1), (2) являются дифференциальными уравнениями материальной точки в векторной форме. Спроектировав оба равенства (1) на оси координат:
 Пусть траектория движения точки известна
Пусть траектория движения точки известна Если траектория точки известна, всегда можно построить естественные оси траектории.
Если траектория точки известна, всегда можно построить естественные оси траектории.



 Момент инерции тела относительно оси является мерой инерции тела во вращательном движении вокруг этой оси.Момент инерции тела может быть также выражен через массу М тела и его радиус инерции r:
Момент инерции тела относительно оси является мерой инерции тела во вращательном движении вокруг этой оси.Момент инерции тела может быть также выражен через массу М тела и его радиус инерции r: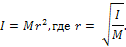 МОМЕНТЫ ИНЕРЦИИ ОТНОСИТЕЛЬНО ОСЕЙ, ПЛОСКОСТЕЙ И НАЧАЛА ДЕКАРТОВЫХ КООРДИНАТ. Осевые моменты инерции:
МОМЕНТЫ ИНЕРЦИИ ОТНОСИТЕЛЬНО ОСЕЙ, ПЛОСКОСТЕЙ И НАЧАЛА ДЕКАРТОВЫХ КООРДИНАТ. Осевые моменты инерции: Моменты инерции относительно плоскостей координат:
Моменты инерции относительно плоскостей координат:




 где
где  - центробежный момент инерции относительно центральных осей хс, yс, параллельных осям х, у; М - масса тела; xс, yс - координаты центра масс в системе осей х, у. ИЗМЕНЕНИЕ ЦЕНТРОБЕЖНОГО МОМЕНТА ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ x, y ВОКРУГ ОСИ z НА УГОЛ α В ПОЛОЖЕНИЕ x1y1 (рис. 3):
- центробежный момент инерции относительно центральных осей хс, yс, параллельных осям х, у; М - масса тела; xс, yс - координаты центра масс в системе осей х, у. ИЗМЕНЕНИЕ ЦЕНТРОБЕЖНОГО МОМЕНТА ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ x, y ВОКРУГ ОСИ z НА УГОЛ α В ПОЛОЖЕНИЕ x1y1 (рис. 3):
 В проекциях на декартовые оси:
В проекциях на декартовые оси: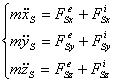 Суммарными характеристиками меры механического движения является: 1) количество движения системы, 2) момент количества движения, 3) кинетическая энергия системы. Две первые меры являются векторными, а последняя – скалярной.
Суммарными характеристиками меры механического движения является: 1) количество движения системы, 2) момент количества движения, 3) кинетическая энергия системы. Две первые меры являются векторными, а последняя – скалярной. называют вектор, равный произведению массы точки на ее скорость, т.е.
называют вектор, равный произведению массы точки на ее скорость, т.е.
 называют векторную сумму количеств движения отдельных точек системы, т.е.
называют векторную сумму количеств движения отдельных точек системы, т.е. Количество движения системы можно выразить через массу системы и скорость центра масс если масса системы не изменяется при движении.
Количество движения системы можно выразить через массу системы и скорость центра масс если масса системы не изменяется при движении. Действие силы
Действие силы 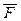 на материальную точку в течении времени
на материальную точку в течении времени 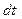 можно охарактеризовать элементарным импульсом силы
можно охарактеризовать элементарным импульсом силы  .Полный импульс силы
.Полный импульс силы  , или импульс силы
, или импульс силы  , определяется по формуле
, определяется по формуле  . Если сила
. Если сила  ),
),  .
.
 на материальную точку в течение времени dt можно охарактеризовать так называемым элементарным импульсом силы
на материальную точку в течение времени dt можно охарактеризовать так называемым элементарным импульсом силы  . Полный импульс силы за время t, или импульс силы определяют по формуле
. Полный импульс силы за время t, или импульс силы определяют по формуле Дифференциальное уравнение движения материальной точки под действием силы
Дифференциальное уравнение движения материальной точки под действием силы  Так как масса точки считается постоянной, то ее можно внести под знак производной. Тогда
Так как масса точки считается постоянной, то ее можно внести под знак производной. Тогда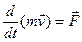 Эта формула выражает теорему об изменении количества движения точки в дифференциальной форме: первая производная по времени от количества движения точки равна действующей на точку силе. (Причиной изменения количества движения точки является сила).В проекциях на оси координат теорема записывается следующим образом:
Эта формула выражает теорему об изменении количества движения точки в дифференциальной форме: первая производная по времени от количества движения точки равна действующей на точку силе. (Причиной изменения количества движения точки является сила).В проекциях на оси координат теорема записывается следующим образом: Если обе части теоремы умножить на dt, то получим другую форму этой же теоремы
Если обе части теоремы умножить на dt, то получим другую форму этой же теоремы .т.е. дифференциал от количества движения точки равен элементарному импульсу силы, действующей на точку.Интегрируя обе части в пределах от нуля до t, имеем:
.т.е. дифференциал от количества движения точки равен элементарному импульсу силы, действующей на точку.Интегрируя обе части в пределах от нуля до t, имеем: .где
.где  -скорость точки в момент t,
-скорость точки в момент t,  -скорость при t=0,
-скорость при t=0,  -импульс силы за время t.Это выражение часто называют теоремой импульсов в конечной (или интегральной) форме: изменение количества движения точки за какой-либо промежуток времени равно импульсу силы за тот же промежуток времени.Для материальной точки теорема об изменении количества движения в любой из форм, по существу, не отличается от дифференциальных уравнений движения точки.
-импульс силы за время t.Это выражение часто называют теоремой импульсов в конечной (или интегральной) форме: изменение количества движения точки за какой-либо промежуток времени равно импульсу силы за тот же промежуток времени.Для материальной точки теорема об изменении количества движения в любой из форм, по существу, не отличается от дифференциальных уравнений движения точки.


