Матрицы и определители
Виды матриц.
- Матрица A размера m×n — это прямоугольная таблица чисел, расположенных в m строках и n столбцах

где aij (i =1, …, m; j =1, …, n) — это элементы матрицы A. Первый индекс i — это номер строки, второй индекс j — это номер столбца, на пересечении которых расположен элемент aij.
Сокращённое обозначение матрицы A=(aij)m×n. - Порядок матрицы — это число ее строк или столбцов.
- Главная диагональ квадратной матрицы — это диагональ, идущая из левого верхнего в правый нижний угол.
- Прямоугольная матрица — это матрица, у которой число строк не равно числу столбцов.
- Квадратная матрица — это матрица у которой число строк равно числу столбцов:
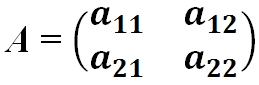
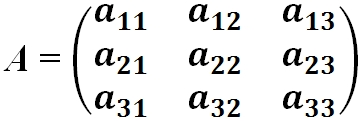
- Матрица-столбец — это матрица, у которой всего один столбец:
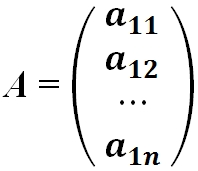
- Матрица-строка — это матрица, у которой всего одна строка:
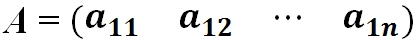
- Диагональная матрица — это квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю.
- Единичная матрица — это диагональная матрица, у которой все диагональные элементы равны единице:
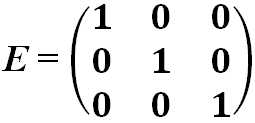
- Матрица квадратная диагональная:
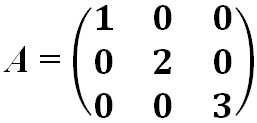
- Треугольная матрица — это квадратная матрица, у которой все элементы, расположенные по одну сторону главной диагонали, равны нулю.
- Матрица верхняя треугольная:
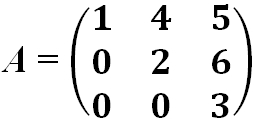
- Матрица нижняя треугольная:
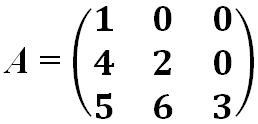
- Нулевая матрица — это матрица, все элементы которой равны 0:
Операции над матрицами.
- Равенство матриц.
Две матрицы A (aij), B (bij) совпадают | A=B |, если совпадают их размеры и соответствующие элементы равны,
то есть при всех i, j aij=bij. - Сложение матриц.
Суммой двух матриц A=(aij)m×n и B=(bij) m×n одинаковых размеров называется матрица C=(cij)m×n=A+B тех же размеров, элементы которой определяются равенствами cij=aij+bij. Пример 1. - Умножение матрицы на число.
Произведением матрицы A=(aij)m×n на число λ ∈ R называется матрица B=(bij)m×n=λA, элементы которой определяются равенствами bij=λaij. Пример 2. - Умножение матриц.
Произведением матрицы A=(aij)m×k на матрицу B=(bij)k×n называется матрица C=(cij)m×n=A· B размера m×n, элементы которой cij определяются равенством
cij=ai1b1j+ai2b2j+ … aikbkj.
Таким образом, элемент матрицы C=A·B, расположенный в i -й строке и j -м столбце, равен сумме произведений элементов i -й строки матрицы A на соответствующие элементы j -го столбца матрицы B. Пример 3. - Транспонированные матрицы.
Транспонированием матрицы А называется замена строк этой матрицы ее столбцами с сохранением их номеров.
Полученная матрица обозначается через A' или AT. Пример 4.
Квадратная матрица называется симметричной, если A=A', то есть для элементов выполнены равенства aij=aji. - Обратная матрица.
Квадратная матрица n –го порядка называется вырожденной, если определитель этой матрицы равен нулю, | A | = 0, и невырожденной, если | A | ≠ 0.
Матрица А-1 называется обратной матрицей для некоторой квадратной матрицы А, если выполняется соотношение:
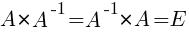
Если матрица А-1 не вырождена, то существует, и притом единственная, обратная матрица А-1, равная 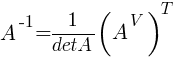 , где АV = Aij — присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).
, где АV = Aij — присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).
1) 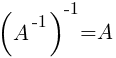
2) 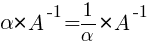
3) 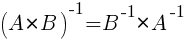
4) 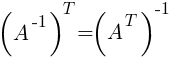
- Алгоритм нахождения А-1 заключается в следующих пунктах:
1) Находим det A, проверяем det A ≠ 0.
2) Находим Mij — все миноры матрицы A.
3) Определяем 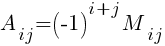
4) Строим матрицу алгебраических дополнений 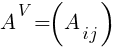 и транспонируем:
и транспонируем: 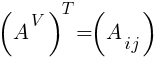
5) Делим каждый элемент матрицы на det A: 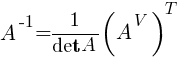 Пример 5.
Пример 5. - Элементарные преобразования строк (столбцов) матрицы:
1) перестановка строк (столбцов);
2) умножение строки (столбца) на число α ≠ 0;
3) прибавление к элементам строки (столбца) матрицы элементов другой строки (столбца), умноженных на некоторое число. - Решение матричных уравнений.
Матричное уравнение — это уравнение, содержащее неизвестную матрицу X и известные матрицы A, B, …,.
Простейшие типы матричных уравнений:
1) 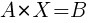 . Матрица A – квадратная и невырожденная,
. Матрица A – квадратная и невырожденная,
| A | ≠ 0, следовательно, существует обратная матрица A-1.
Умножим уравнение на A-1 слева: 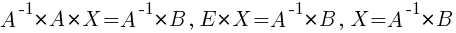
2) 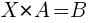 . Матрица A – квадратная, | A | ≠ 0.
. Матрица A – квадратная, | A | ≠ 0.
Умножим уравнение на A-1 справа: 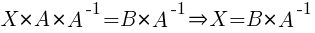 .
.
3) 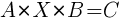 . Матрицы A и B – квадратные, | A | ≠ 0, | B | ≠ 0.
. Матрицы A и B – квадратные, | A | ≠ 0, | B | ≠ 0.
Умножим уравнение на A-1 слева: 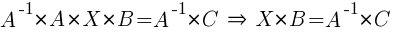
Умножим уравнение на B-1 справа: 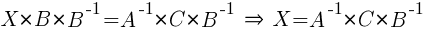 .
. - Ранг матрицы.
Ранг матрицы A — это число, равное максимальному порядку отличных от нуля миноров.
Mk этой матрицы: 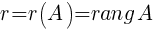
Матрицы называются эквивалентными, что обозначается
A ∼ B, если 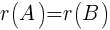 .
.
Ранг матрицы A вычисляется методом окаймляющих миноров или методом элементарных преобразований. - Метод окаймляющих миноров.
Пусть в матрице A элемент aij ≠ 0, тогда M1 ≠ 0 и r(A) ≥ 1. Окаймляем этот элемент элементами соседнего столбца и соседней строки (например, (j +1)–го столбца и (i +1)–й строки), получаем минор 2-го порядка: 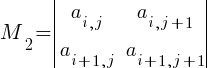 .
.
Если M2, то присоединяем другие строки и столбцы, перебирая все возможные миноры 2-го порядка.
Если все миноры второго порядка равны нулю, то r(A) = 1; если же существует хотя бы один минор 2-го порядка, отличный от нуля, то r(A) ≥ 1.
Выбираем отличный от нуля минор 2-го порядка M2 и окаймляем его элементами соседних строк и столбцов до минора 3-го порядка и так до тех пор, пока не будет выполнено условие: Mr ≠ 0, но все Mr+1 = 0. Пример 6. - Метод элементарных преобразований.
Элементарные преобразования матрицы не меняют ее ранга.
К элементарным преобразованиям матрицы относятся следующие: транспонирование; перестановка строк (столбцов); умножение строки (столбца) на число α ≠ 0; прибавление к элементам строки (столбца) матрицы элементов другой строки, умноженных на некоторое число; отбрасывание нулевой строки (столбца) матрицы.
Для определения ранга матрицы A методом элементарных преобразований следует:
1) Переставить строки и столбцы так, чтобы в верхнем левом углу матрицы был ненулевой элемент.
2) Все элементы первого столбца, кроме a11, обратить в ноль с помощью элементарных преобразований строк:
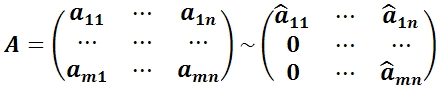
3) Переставить строки со 2–й по m и столбцы со 2–го по n так, чтобы a22 ≠ 0. Повторить операцию (2) со вторым столбцом: во втором столбце все элементы, кроме a12 и a22, обратить в ноль.
Окончательно после многократного применения указанной процедуры и отбрасывания нулевых строк преобразованная матрица будет иметь вид:
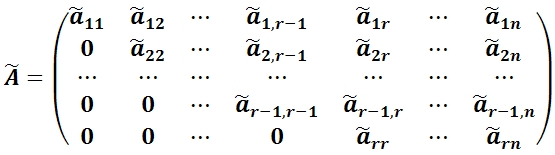
Тогда ранг матрицы A равен: rang A = rang Ã.
Определители
Определитель квадратной матрицы A =[ n × n ] — это объём n
-мерного параллелепипеда, который образуется, если рассмотреть строки матрицы в качестве векторов, образующих рёбра этого параллелепипеда.
Например, определитель матрицы размера 2x2 — это просто площадь параллелограмма, а для матрицы 3x3 это уже объём 3-мерного параллелепипеда — того самого, который так бесит всех старшеклассников на уроках стереометрии.
Определитель (детерминант) квадратной матрицы A — это число det A, которое ставится в соответствие матрице
Всякой квадр. матрице можно поставить в соответсвие число (определитель или дертеминант) det A n=1 A=(a11) det=|a11|= a11
n=2 A= 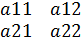 det=
det= 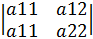 =a11*a22-a12*a21
=a11*a22-a12*a21
Определитель матрицы.
- Определитель квадратной матрицы.
Определитель первого порядка представляет собой число.
Определитель квадратной матрицы порядка n A=(aij)m×n обозначается символами: 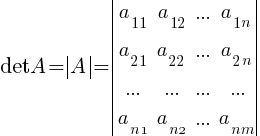
Определитель квадратной матрицы A второго порядка — это число, равное: 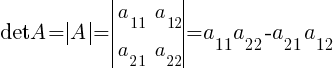
Определитель квадратной матрицы А третьего порядка — это число, равное:
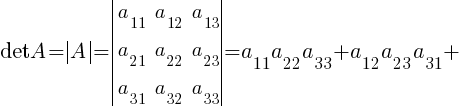
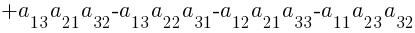 . Пример 7.
. Пример 7. - Правило треугольников (правило Саррюса):
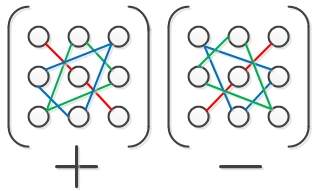
Знаки (+) и (–) соответствуют знакам определенных слагаемых, входящих в определитель, элементы определителя изображаются кружками, а соответствующие произведения — отрезками или треугольниками. - Алгебраическое дополнение A=(aij) элемента aij — это определитель n -1 порядка, полученный из | A | вычеркиванием i -й строки и j -го столбца, на пересечении которых стоит элемент aij, взятый со знаком (-1)i+j.
Свойства определителей.
- Определитель квадратной матрицы А не меняется при транспонировании: | AT |=| A |.
- При перестановке местами любых двух строк (столбцов) определитель | A | меняет знак:
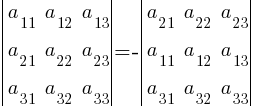
- Определитель, содержащий две одинаковые строки (столбца), равен нулю.
- Умножение всех элементов некоторой строки (столбца) определителя | A | на число k равносильно умножению определителя на это число:
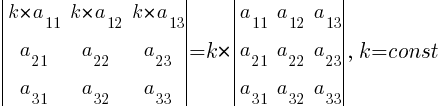
- Если все элементы некоторой строки (столбца) определителя | A | равны нулю, то и сам определитель равен нулю (вытекает из предыдущего свойства при (k = 0):
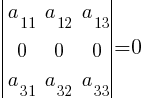
- Если все элементы двух строк (столбцов) определителя | A | пропорциональны, то определитель равен нулю.
- Если каждый элемент некоторой строки (столбца) определителя представляет собой сумму двух слагаемых, то такой определитель можно представить в виде суммы двух определителей:
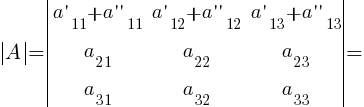
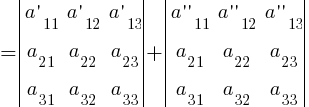
- Если к элементам какой-нибудь строки (столбца) определителя | A | прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель k, то величина определителя не изменится:
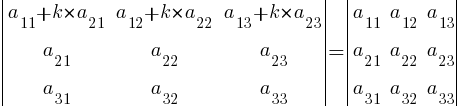
- Определитель | A | численно равен сумме произведений элементов любой его строки (столбца) на соответствующие алгебраические дополнения:
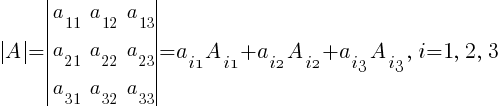
- Определитель произведения матриц А и В равен произведению их определителей:
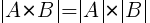 .
.
Определители n –го порядка.
- Минор Мij или Δij элемента аij (иначе – дополнительный минор элемента аij) определителя n -го порядка — это определитель (n–1) порядка, полученный из исходного вычеркиванием i –й строки и j –го столбца, на пересечении которых стоит элемент aij.
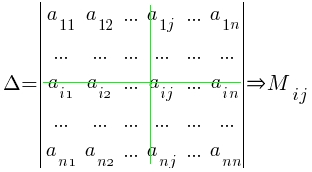
- Алгебраическое дополнение Аij элемента аij — это его минор со знаком (-1)i+j, где i – номер строки, а j – номер столбца, на пересечении которых стоит элемент aij, Аij=(-1)i+jMij или Аij=(-1)i+jΔij. Пример 8.
Для определителей n -го порядка имеют место все перечисленные выше свойства определителей. - Правило выбора знака перед минором в алгебраическом дополнении:
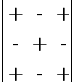
- Определитель n -го порядка | A | численно равен сумме произведений элементов любой его строки (столбца) на соответствующие алгебраические дополнения.
- Метод сведения к треугольному виду.
Используя свойства (1–9), определитель преобразуют к виду, когда элементы, лежащие по одну сторону от главной диагонали, становятся равными нулю. Преобразованный таким образом определитель равен произведению элементов, лежащих на главной диагонали.
Минор (линейная алгебра)
Материал из Википедии — свободной энциклопедии
Перейти к навигации Перейти к поиску
У этого термина существуют и другие значения, см. Минор (значения).
Минор A [ α 1 α 2 … α k β 1 β 2 … β k ] {\displaystyle A{\begin{bmatrix}\alpha _{1}&\alpha _{2}\dots \alpha _{k}\\\beta _{1}&\beta _{2}\dots \beta _{k}\end{bmatrix}}} матрицы A {\displaystyle A} ― определитель такой квадратной матрицы B {\displaystyle B} порядка k {\displaystyle k} (который называется также порядком этого минора), элементы которой стоят в матрице A {\displaystyle A} на пересечении строк с номерами α 1, α 2, …, α k {\displaystyle \alpha _{1},\alpha _{2},\dots,\alpha _{k}} и столбцов с номерами β 1, β 2, …, β k {\displaystyle \beta _{1},\beta _{2},\dots,\beta _{k}}.
Если номера отмеченных строк совпадают с номерами отмеченных столбцов, то минор называется главным, а если отмечены первые k {\displaystyle k} строк и первые k {\displaystyle k} столбцов ― угловым или ведущим главным.
Дополнительный минор элемента матрицы n {\displaystyle n} -го порядка есть определитель порядка n − 1 {\displaystyle n-1}, соответствующий той матрице, которая получается из матрицы путём вычеркивания i {\displaystyle i} -й строки и j {\displaystyle j} -го столбца.
Базисным минором матрицы называется любой её ненулевой минор максимального порядка. Для того чтобы минор был базисным, необходимо и достаточно, чтобы все окаймляющие его миноры (то есть содержащие его миноры на единицу большего порядка) были равны нулю. Система строк (столбцов) матрицы, связанных с базисным минором, является максимальной линейно независимой подсистемой системы всех строк (столбцов) матрицы.
Пример
Дана матрица:
(1 4 7 3 0 5 − 1 9 11) {\displaystyle {\begin{pmatrix}\,\,\,1&4&7\\\,\,\,3&0&5\\-1&9&\!11\\\end{pmatrix}}}
Предположим, необходимо найти дополнительный минор второго порядка M 23 {\displaystyle M_{23}}. Этот минор получается путём вычеркивания второй строки и третьего столбца:
| 1 4 ◻ ◻ ◻ ◻ − 1 9 ◻ | {\displaystyle {\begin{vmatrix}\,\,1&4&\Box \,\\\,\Box &\Box &\Box \,\\-1&9&\Box \,\\\end{vmatrix}}} ⟶ {\displaystyle \longrightarrow } | 1 4 − 1 9 | = 1 ⋅ 9 − 4 ⋅ (− 1) = 13 {\displaystyle {\begin{vmatrix}\,\,\,1&4\,\\-1&9\,\\\end{vmatrix}}=1\cdot 9-4\cdot (-1)=13}
Получаем M 23 = 13 {\displaystyle M_{23}=13}
Понятие ранга матрицы
Ранг матрицы используется при проверке условия совместности системы линейных уравнений.
Определение. Рангом матрицы называется максимальное число линейно независимых строк, рассматриваемых как векторы.
Можно открыть в новом окне материал о линейной независимости векторов.
Теорема 1 о ранге матрицы. Рангом матрицы называется максимальный порядок отличного от нуля минора матрицы.
Понятие минора мы уже разбирали на уроке по определителям, а сейчас обобщим его. Возьмём в матрице сколько-то строк и сколько-то столбцов, причём это "сколько-то" должно быть меньше числа строк и стобцов матрицы, а для строк и столбцов это "сколько-то" должно быть одним и тем же числом. Тогда на пересечении скольки-то строк и скольки-то столбцов окажется матрица меньшего порядка, чем наша исходная матрица. Определитель это матрицы и будет минором k-го порядка, если упомянутое "сколько-то" (число строк и столбцов) обозначим через k.
Определение. Минор (r +1)-го порядка, внутри которого лежит выбранный минор r -го порядка, называется называется окаймляющим для данного минора.
Наиболее часто используются два способа отыскания ранга матрицы. Это способ окаймляющих миноров и способ элементарных преобразований (методом Гаусса).
При способе окаймляющих миноров используется следующая теорема.
Теорема 2 о ранге матрицы. Если из элементов матрицы можно составить минор r -го порядка, не равный нулю, то ранг матрицы равен r.
При способе элементарных преобразований используется следующее свойство:
- если путём элементарных преобразований получена трапециевидная матрица, эквивалентная исходной, то рангом этой матрицы является число строк в ней кроме строк, полностью состоящих из нулей.
Формулы Крамера
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.
Определение. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается  (дельта).
(дельта).
Определители 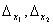
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
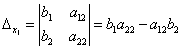 ;
;
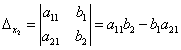 .
.
Формулы Крамера для нахождения неизвестных:
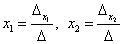 .
.
Найти значения 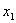 и
и 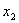 возможно только при условии, если
возможно только при условии, если
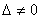 .
.
Этот вывод следует из следующей теоремы.
Теорема Крамера. Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
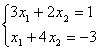 . (2)
. (2)
Согласно теореме Крамера имеем:
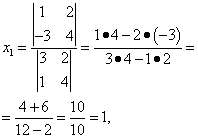
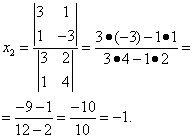
Итак, решение системы (2):
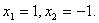
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.
Примеры решения систем линейных уравнений методом Крамера
Пусть дана система
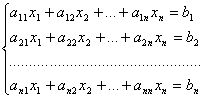 .
.
На основании теоремы Крамера
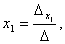
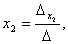
………….
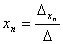 ,
,
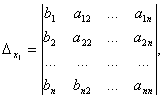
где
 -
-
определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:


Пример 2. Решить систему линейных уравнений методом Крамера:
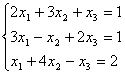 .
.
Решение. Находим определитель системы:
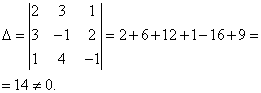
Следовательно, система является определённой. Для нахождения её решения вычисляем определители
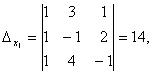
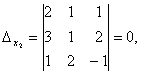
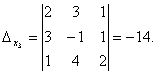
По формулам Крамера находим:
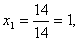
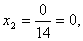
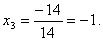
Итак, (1; 0; -1) – единственное решение системы.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.
Пример 3. Решить систему линейных уравнений методом Крамера:
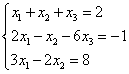 .
.
Решение. Находим определитель системы:
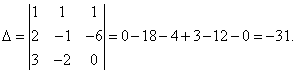
Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных
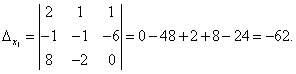
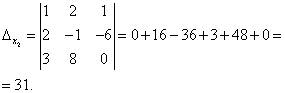

По формулам Крамера находим:
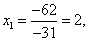
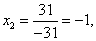
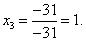
Итак, решение системы - (2; -1; 1).
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.
Понятие вектора
Векторы занимают особое место среди объектов, рассматриваемых в высшей математике, поскольку каждый вектор имеет не только числовое значение - длину, но и физическое и геометрическое - направленность. Вектор, представленный направленным отрезком, идущим от точки A к точке B, обозначается так:  .
.
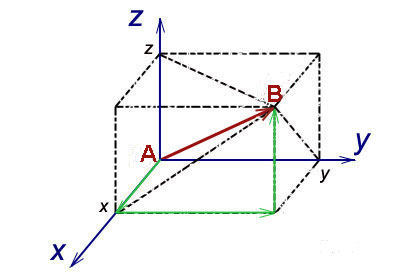
Вектор - это вид представления точки, до которой требуется добраться из некоторой начальной точки. Например, трёхмерный вектор, как правило, записывается в виде (х, y, z). Говоря совсем просто, эти числа означают, как далеко требуется пройти в трёх различных направлениях, чтобы добраться до точки.
Пусть дан вектор. При этом x = 3 (правая рука указывает направо), y = 1 (левая рука указывает вперёд), z = 5 (под точкой стоит лестница, ведущая вверх). По этим данным вы найдёте точку, проходя 3 метра в направлении, указываемом правой рукой, затем 1 метр в направлении, указываемом левой рукой, а далее Вас ждёт лестница и, поднимаясь на 5 метров, Вы, наконец, окажетесь в конечной точке.
Все остальные термины - это уточнения представленного выше объяснения, необходимые для различных операций над векторами, то есть, решения практических задач. Пройдёмся по этим более строгим определениям, останавливаясь на типичных задачах на векторы.
Физическими примерами векторных величин могут служить смещение материальной точки, двигающейся в пространстве, скорость и ускорение этой точки, а также действующая на неё сила.
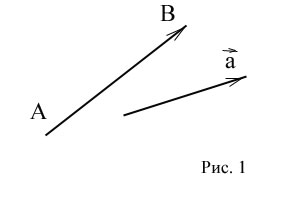 Геометрический вектор представлен в двумерном и трёхмерном пространстве в виде направленного отрезка. Это отрезок, у которого различают начало и конец.
Геометрический вектор представлен в двумерном и трёхмерном пространстве в виде направленного отрезка. Это отрезок, у которого различают начало и конец.
Если A - начало вектора, а B - его конец, то вектор обозначается символом  или одной строчной буквой
или одной строчной буквой 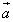 . На рисунке конец вектора указывается стрелкой (рис. 1)
. На рисунке конец вектора указывается стрелкой (рис. 1)
Длиной (или модулем) геометрического вектора 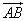 называется длина порождающего его отрезка
называется длина порождающего его отрезка 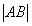
Два вектора называются равными, если они могут быть совмещены (при совпадении направлений) путём параллельного переноса, т.е. если они параллельны, направлены в одну и ту же сторону и имеют равные длины.
В физике часто рассматриваются закреплённые векторы, заданные точкой приложения, длиной и направлением. Если точка приложения вектора не имеет значения, то его можно переносить, сохраняя длину и направление в любую точку пространства. В этом случае вектор называется свободным. Мы договоримся рассматривать только свободные векторы.
Проекция вектора на ось
Проекция вектора на ось равна произведению длины проектируемого вектора на косинус угла между вектором и осью:
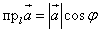
Как известно, проекцией точки A на прямую (плоскость) служит основание 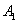 перпендикуляра
перпендикуляра 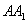 , опущенного из этой точки на прямую (плоскость).
, опущенного из этой точки на прямую (плоскость).
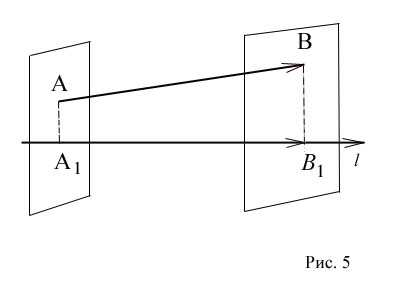
Пусть 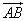 - произвольный вектор (Рис. 5), а
- произвольный вектор (Рис. 5), а 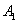 и
и 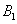 - проекции его начала (точки A) и конца (точки B) на ось l. (Для построения проекции точки A) на прямую проводим через точку A плоскость, перпендикулярную прямой. Пересечение прямой и плоскости определит требуемую проекцию.
- проекции его начала (точки A) и конца (точки B) на ось l. (Для построения проекции точки A) на прямую проводим через точку A плоскость, перпендикулярную прямой. Пересечение прямой и плоскости определит требуемую проекцию.
Составляющей вектора 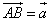 на оси l называется такой вектор
на оси l называется такой вектор 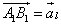 , лежащий на этой оси, начало которого совпадает с проекцией начала, а конец - с проекцией конца вектора
, лежащий на этой оси, начало которого совпадает с проекцией начала, а конец - с проекцией конца вектора 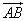 .
.
Проекцией вектора 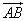 на ось l называется число
на ось l называется число
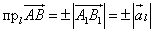 ,
,
равное длине составляющего вектора на этой оси, взятое со знаком плюс, если направление составляюшей совпадает с направлением оси l, и со знаком минус, если эти направления противоположны.
Основные свойства проекций вектора на ось:
1. Проекции равных векторов на одну и ту же ось равны между собой.
2. При умножении вектора на число его проекция умножается на это же число.
3. Проекция суммы векторов на какую-либо ось равна сумме проекций на эту же ось слагаемых векторов.
4. Проекция вектора на ось равна произведению длины проектируемого вектора на косинус угла между вектором и осью:
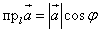
Пример 5. Рассчитать проекцию суммы векторов 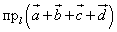 на ось l, если
на ось l, если 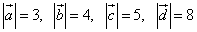 , а углы -
, а углы -
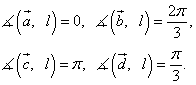 .
.
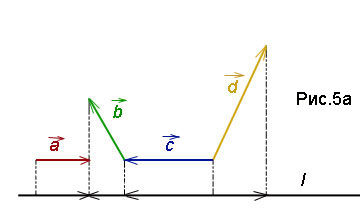 Решение. Спроектируем векторы на ось l как определено в теоретической справке выше. Из рис.5а очевидно, что проекция суммы векторов равна сумме проекций векторов. Вычисляем эти проекции:
Решение. Спроектируем векторы на ось l как определено в теоретической справке выше. Из рис.5а очевидно, что проекция суммы векторов равна сумме проекций векторов. Вычисляем эти проекции:
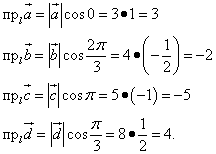
Находим окончательную проекцию суммы векторов:
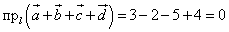 .
.
Равенство (2) называется разложением вектора по координатным осям. Коэффициентами этого разложения являются проекции вектора на координатные оси. Таким образом, коэффициентами разложения (2) вектора по координатным осям являются координаты вектора.
После выбора в пространстве определённой системы координат вектор и тройка его координат однозначно определяют друг друга, поэтому вектор может быть записан в форме
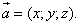 (3)
(3)
Представления вектора в виде (2) и (3) тождественны.
Правильное решение и ответ
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Векторы
n -мерные векторы и операции над ними
При изучении многих вопросов, в частности, экономических, оказалось удобным обобщить рассмотренные приёмы установления соответствия между числами и точками двумерного и трёхмерного пространства и рассматривать последовательности n действительных чисел как "точки" некоторого абстрактного " n -мерного пространства", а сами числа - как "координаты" этих точек. За составляющие n -мерного вектора можно принимать такие данные, как урожайность различных культур, объёмы продаж товаров, технические коэффициенты, номенклатура товаров на складах и т.д.
n-мерным вектором называется упорядоченный набор из n действительных чисел, записываемых в виде
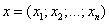 ,
,
где 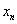 - i – й элемент (или i – я координата) вектора x.
- i – й элемент (или i – я координата) вектора x.
Возможна и другая запись вектора – в виде столбца координат:
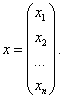
Размерность вектора определяется числом его координат и является его отличительной характеристикой. Например, (2; 5) – двухмерный вектор, (2; -3; 0) – трёхмерный, (1; 3; -2; -4; 7) – пятимерный,
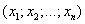 -
-
n – мерный вектор.
Нулевым вектором называется вектор, все координаты которого равны нулю:
0 = (0; 0; …; 0).
Введём операции над n -мерными векторами.
Произведением вектора
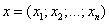
на действительное число 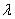 называется вектор
называется вектор
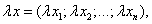
(при умножении вектора на число каждая его координата умножается на это число).
Зная вектор
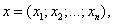
можно получить противоположный вектор

Суммой векторов
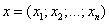
и
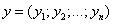
называется вектор
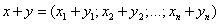 ,
,
(при сложении векторов одной и той же размерности их соответствующие координаты почленно складываются).
Если в плане продаж сети торговых предприятий продажи товаров определить как положительные уровни товаров, а затраты на продажи – как отрицательные, то получим вектор затрат-продаж
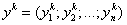 ,
,
где
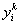 -
-
продажи (затраты) k – м предприятием товара i, а k = 1, 2, 3,…, m.
Суммарный вектор затрат-продаж y определяется суммированием векторов затрат-продаж всех m предприятий сети:
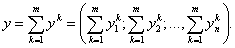
Сумма противоположных векторов даёт нулевой вектор:
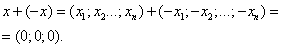
При вычитании двух векторов одной и той же размерности их соответствующие координаты почленно вычитаются:
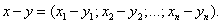
Операции над n -мерными векторами удовлетворяют следующим свойствам.
Свойство 1.
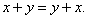
Свойство 2.
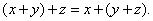
Свойство 3.
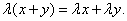
Свойство 4.

Свойство 5.
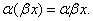
Свойство 6.
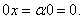
Геометрические свойства
Теорема 1. Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю векторного произведения этих векторов.
Теорема 2. Длина (или модуль) векторного произведения векторов 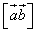 равна площади S параллелограмма, построенного на приведённых к общему началу векторах
равна площади S параллелограмма, построенного на приведённых к общему началу векторах 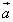 и
и 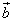 .
.
Следствие. Площадь треугольника, построенного на приведённых к общему началу векторах 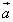 и
и 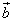 , равна половине длины векторного произведения этих векторов.
, равна половине длины векторного произведения этих векторов.
Пример 3. Найти
1) площадь параллелограмма, построенного на векторах 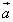 и
и 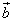 из примера 1;
из примера 1;
2) площадь треугольника, построенного на тех же векторах.
Решение:
1) из примера 1, где была найдена длина векторного произведения данных векторов, получаем, 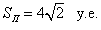
2) требуемая площадь треугольника равна половине длины векторного произведения векторов, или, что то же самое, половине площади параллелограмма, т.е. 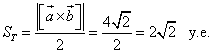
Пример 4. Вычислить площадь треугольника ABC, если известны координаты его вершин:
A (3; 1; -1), B (-1; 0; 2), C (3; 2; -2).
Решение. Найдём координаты векторов 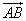 и
и 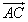 :
:
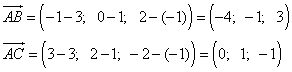
Площадь треугольника равна половине длины векторного произведения векторов, на которых он построен. Найдём векторное произведение через координаты векторов:
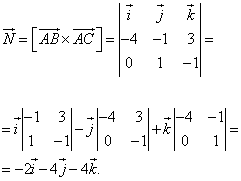
То есть, координаты вектора, являющегося векторным произведением исходных векторов:
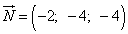 , откуда найдём его длину:
, откуда найдём его длину:
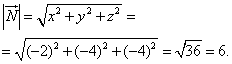
Теперь получим требуемую сумму треугольника:
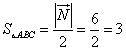 .
.
Алгебраические свойства
1. 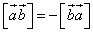 (свойство антиперестановочности сомножителей);
(свойство антиперестановочности сомножителей);
2. 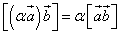 (сочетательное относительно числового множителя свойство);
(сочетательное относительно числового множителя свойство);
3. 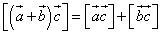 (распределительное относительно суммы векторов свойство);
(распределительное относительно суммы векторов свойство);
4. 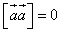 для любого вектора
для любого вектора  .
.
Матрицы и определители
Виды матриц.
- Матрица A размера m×n — это прямоугольная таблица чисел, расположенных в m строках и n столбцах

где aij (i =1, …, m; j =1, …, n) — это эл



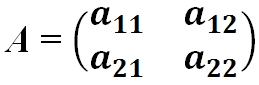
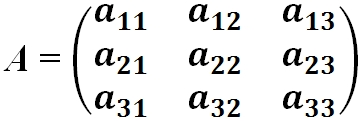
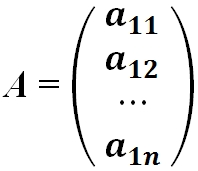
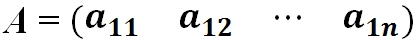
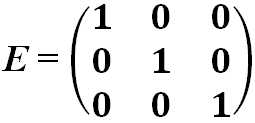
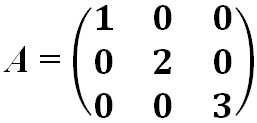
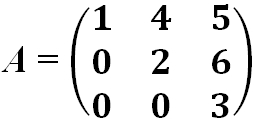
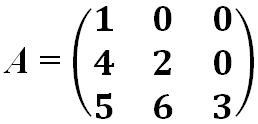

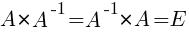
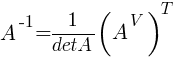 , где АV = Aij — присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).
, где АV = Aij — присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).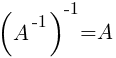
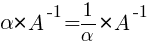
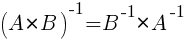
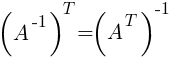
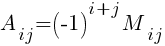
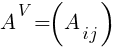 и транспонируем:
и транспонируем: 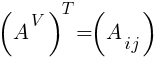
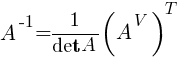 Пример 5.
Пример 5.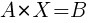 . Матрица A – квадратная и невырожденная,
. Матрица A – квадратная и невырожденная,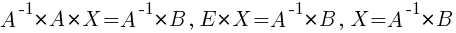
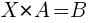 . Матрица A – квадратная, | A | ≠ 0.
. Матрица A – квадратная, | A | ≠ 0.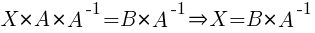 .
.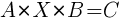 . Матрицы A и B – квадратные, | A | ≠ 0, | B | ≠ 0.
. Матрицы A и B – квадратные, | A | ≠ 0, | B | ≠ 0.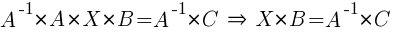
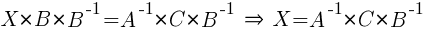 .
.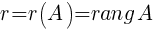
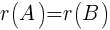 .
.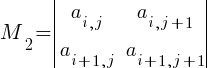 .
.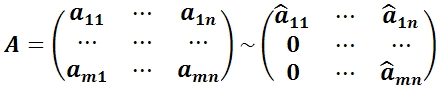
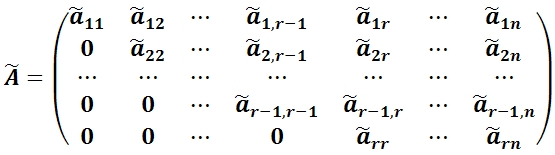
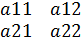 det=
det= 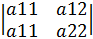 =a11*a22-a12*a21
=a11*a22-a12*a21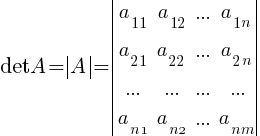
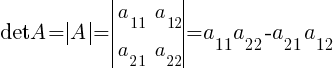
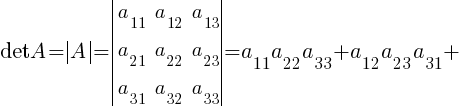
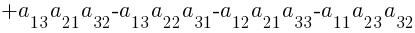 . Пример 7.
. Пример 7. 
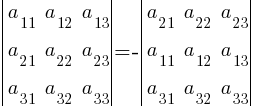
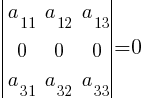
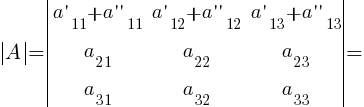
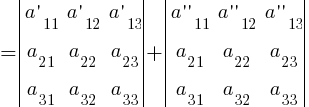
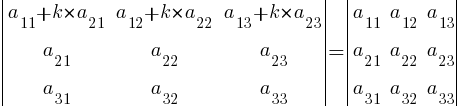
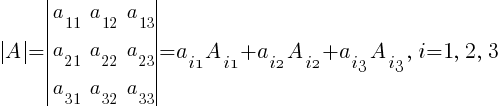
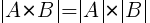 .
.

 (дельта).
(дельта).
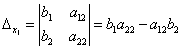 ;
;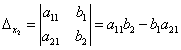 .
.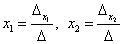 .
.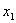 и
и 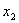 возможно только при условии, если
возможно только при условии, если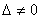 .
.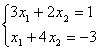 . (2)
. (2)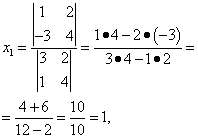
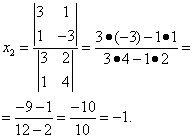
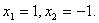
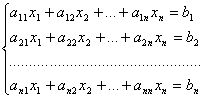 .
.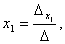
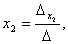
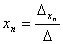 ,
, -
-


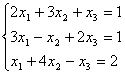 .
.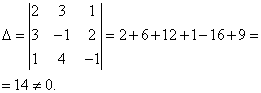
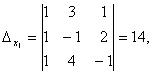
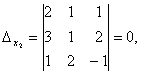
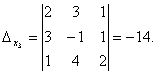
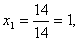
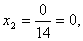
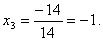
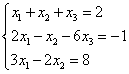 .
.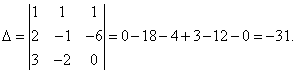
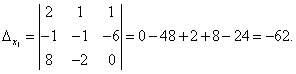
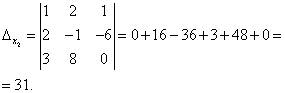

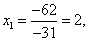
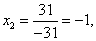
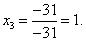
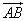 .
.
 Геометрический вектор представлен в двумерном и трёхмерном пространстве в виде направленного отрезка. Это отрезок, у которого различают начало и конец.
Геометрический вектор представлен в двумерном и трёхмерном пространстве в виде направленного отрезка. Это отрезок, у которого различают начало и конец.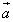 . На рисунке конец вектора указывается стрелкой (рис. 1)
. На рисунке конец вектора указывается стрелкой (рис. 1)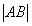
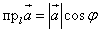
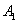 перпендикуляра
перпендикуляра 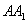 , опущенного из этой точки на прямую (плоскость).
, опущенного из этой точки на прямую (плоскость).
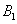 - проекции его начала (точки A) и конца (точки B) на ось l. (Для построения проекции точки A) на прямую проводим через точку A плоскость, перпендикулярную прямой. Пересечение прямой и плоскости определит требуемую проекцию.
- проекции его начала (точки A) и конца (точки B) на ось l. (Для построения проекции точки A) на прямую проводим через точку A плоскость, перпендикулярную прямой. Пересечение прямой и плоскости определит требуемую проекцию.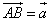 на оси l называется такой вектор
на оси l называется такой вектор 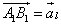 , лежащий на этой оси, начало которого совпадает с проекцией начала, а конец - с проекцией конца вектора
, лежащий на этой оси, начало которого совпадает с проекцией начала, а конец - с проекцией конца вектора 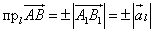 ,
,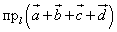 на ось l, если
на ось l, если 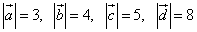 , а углы -
, а углы -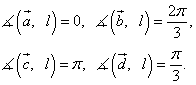 .
. Решение. Спроектируем векторы на ось l как определено в теоретической справке выше. Из рис.5а очевидно, что проекция суммы векторов равна сумме проекций векторов. Вычисляем эти проекции:
Решение. Спроектируем векторы на ось l как определено в теоретической справке выше. Из рис.5а очевидно, что проекция суммы векторов равна сумме проекций векторов. Вычисляем эти проекции: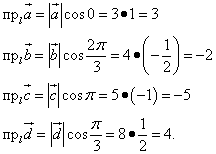
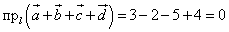 .
.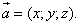 (3)
(3)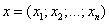 ,
,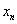 - i – й элемент (или i – я координата) вектора x.
- i – й элемент (или i – я координата) вектора x.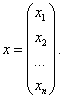
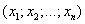 -
-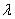 называется вектор
называется вектор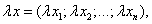
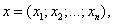

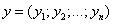
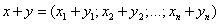 ,
,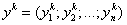 ,
,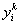 -
-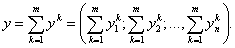
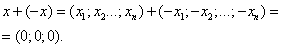
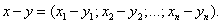
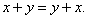
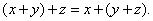
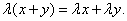

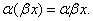
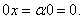
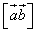 равна площади S параллелограмма, построенного на приведённых к общему началу векторах
равна площади S параллелограмма, построенного на приведённых к общему началу векторах 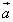 и
и 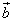 .
.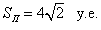
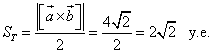
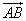 и
и 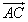 :
: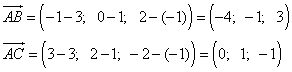
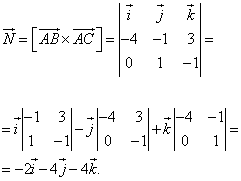
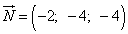 , откуда найдём его длину:
, откуда найдём его длину: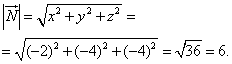
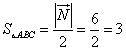 .
.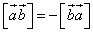 (свойство антиперестановочности сомножителей);
(свойство антиперестановочности сомножителей);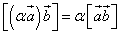 (сочетательное относительно числового множителя свойство);
(сочетательное относительно числового множителя свойство);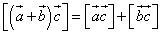 (распределительное относительно суммы векторов свойство);
(распределительное относительно суммы векторов свойство);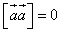 для любого вектора
для любого вектора