Из опытов, проведенных Бриджменом и другими исследователями, определенно следует, что наложение гидростатического (всестороннего) давления на одноосное растяжение может значительно увеличить ресурс пластичности материала. Дальнейшие исследования подтвердили существенное влияние вида напряженного состояния на величину деформации, предшествующей разрушению.
С именем А. Cен-Венана* связывают, по-видимому, исторически первый критерий разрушения деформационного типа. В соответствии с гипотезой наибольших деформаций, известной ныне как вторая теория прочности, разрушение независимо от вида напряженного состояния происходит при достижении наибольшим (по модулю) из компонентов деформации предельного для данного материала значения:
e 1 = e ВР (или, при e 3 < 0, e 3 = e ВС). (14)
Однако ряд обстоятельств (в первую очередь, предположение о независимости предельной деформации от вида напряженного состояния, формулировка гипотезы в терминах напряжений с использованием закона Гука:

(m – коэффициент Пуассона), означающая, что материал работает упруго вплоть до разрушения, в то время, как разрушение отрывного типа критерий (14) не описывает) обусловили противоречие данным опытов над пластичными материалами. Поэтому в настоящее время вторая теория прочности имеет ограниченное применение в инженерной практике.
Деформационный подход к разработке критериев разрушения был развит в теоретических и экспериментальных исследованиях В. Л. Колмогорова** с сотрудниками, в результате чего удалось сформулировать один из наиболее адекватных в рассматриваемых условиях критерий вязкого разрушения. На основе обобщения весьма представительной выборки экспериментальных данных так называемый деформационный критерий устанавливает связь между предельной неупругой деформацией и специальной характеристикой напряженного состояния, которую авторы назвали параметром жесткости напряженного состояния, представляющим отношение среднего нормального напряжения  к интенсивности напряжений s И (8). Таким образом, этот критерий вносит существенную поправку в формулировку гипотезы наибольших деформаций (14) – своего прямого исторического предшественника.
к интенсивности напряжений s И (8). Таким образом, этот критерий вносит существенную поправку в формулировку гипотезы наибольших деформаций (14) – своего прямого исторического предшественника.
Дальнейший анализ показал, что экспериментальные зависимости предельной интенсивности деформации  от отношения s 0/ s И(рис. 15)
от отношения s 0/ s И(рис. 15)
 * Сен-Венан, Адемар Жан-Клод Барре (1797 – 1886) – французский механик и инженер, один из основоположников сопротивления материалов, теории упругости и основ теории пластичности. Получил решение задач изгиба и кручения стержней. Изучал деформирование прямых и кривых (в том числе, пружин) стержней, чистый изгиб стержня за пределами упругости, удар и колебания балок. Читал лекции по механике в Школе мостов и дорог, Агроинженерном институте в Версале. С 1868 г. – действительный член Парижской академии наук.
* Сен-Венан, Адемар Жан-Клод Барре (1797 – 1886) – французский механик и инженер, один из основоположников сопротивления материалов, теории упругости и основ теории пластичности. Получил решение задач изгиба и кручения стержней. Изучал деформирование прямых и кривых (в том числе, пружин) стержней, чистый изгиб стержня за пределами упругости, удар и колебания балок. Читал лекции по механике в Школе мостов и дорог, Агроинженерном институте в Версале. С 1868 г. – действительный член Парижской академии наук.
** Колмогоров, Вадим Леонидович (1931 – 2012) – механик, член-корреспондент РАН, доктор технических наук, профессор. С мая 1986 года работал заместителем директора Института машиноведения УрО РАН. Под его руководством и непосредственном участии разработана феноменологическая теория разрушения, обобщающая обширные экспериментальные данные и разработана методика получения ее определяющих соотношений. Теория описывает процессы развития, торможения и «залечивания» микродефектов. Другим фундаментальным научным и прикладным результатом, полученным им, является создание теории пластогидродинамического трения и соответствующей технологии обработки металлов давлением [6]. В.Л.Колмогоров награжден орденами «Октябрьская революция» и «Трудовое красное знамя», а также медалью «За доблестный труд». Лауреат премии Совета министров СССР.

|
| Рис. 15. Зависимость интенсивности логарифмической пластической деформации в момент разрушения от параметра жесткости напряженного состояния
|
могут быть с достаточной для практических целей точностью аппроксимированы экспоненциальной функцией, содержащей два параметра,

(данная формулировка деформационного критерия предложена К.М. Кононовым*). Используя уравнение единой кривой (7), связывающей интенсивности напряжений и деформаций, последнее выражение можно привести к виду
 . (15)
. (15)
Для определения постоянных a и b достаточно данных двух экспериментов, выполненных при простых видах нагружения – растяжении, чистом сдвиге или сжатии, причем сочетание первых двух предпочтительнее (см. замечание в подразделе 5.1).
При растяжении имеем  ; тогда из формулы (15) следует, что эти две константы взаимосвязаны:
; тогда из формулы (15) следует, что эти две константы взаимосвязаны:
b = -3 ln a. (16)
При чистом сдвиге – 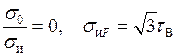 – получим
– получим
 . (17)
. (17)
 * Кононов, Константин Михайлович (1934 – 2001) – канд. техн. наук, доцент кафедры «Сопротивление материалов, динамика и прочность машин» ЧПИ – ЧГТУ – ЮУрГУ. Руководитель кафедрального отдела экспериментальных исследований, разработчик курса «Конструкционная прочность» для студентов специальности «Динамика и прочность машин». Соавтор трех монографий, около 80 научных статей и ряда учебных пособий.
* Кононов, Константин Михайлович (1934 – 2001) – канд. техн. наук, доцент кафедры «Сопротивление материалов, динамика и прочность машин» ЧПИ – ЧГТУ – ЮУрГУ. Руководитель кафедрального отдела экспериментальных исследований, разработчик курса «Конструкционная прочность» для студентов специальности «Динамика и прочность машин». Соавтор трех монографий, около 80 научных статей и ряда учебных пособий.
Интенсивность предельной пластической деформации в этом случае составит  (gpF – пластическая деформация сдвига в момент разрушения).
(gpF – пластическая деформация сдвига в момент разрушения).
С учетом этих результатов деформационный критерий в терминах напряжений (15) можно представить в довольно простой форме:
 . (18)
. (18)
С помощью зависимости (18) и данных опытов (t В,  ) можно найти предельную интенсивность напряжений s И F и соответствующую ей интенсивность деформаций для рассматриваемого материала (см. (7))
) можно найти предельную интенсивность напряжений s И F и соответствующую ей интенсивность деформаций для рассматриваемого материала (см. (7))
 (19)
(19)
при произвольном напряженном состоянии.
Формулы (18), (19) удобно использовать, определяя, например, координаты точек на единой кривой деформирования, отвечающих моменту разрушения (см. рис. 11).
Сопоставляя формулу (15) с учетом определений (16), (17) с общей формой критериев разрушения (10), заключаем, что выражение для эквивалентного напряжения по деформационному критерию имеет вид
 .
.
Примечательно, что согласно данному критерию существует однозначная связь между основными характеристиками прочности. Поскольку
при одноосном сжатии  , из равенства (18) следует
, из равенства (18) следует
 ,
,
откуда нетрудно по известным двум характеристикам получить значение третьей, а также величину коэффициента разнопрочности
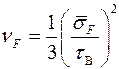 .
.
Необходимо отметить, что значения коэффициента n F для одного и того же материала,рассчитанные с помощью разных критериев, не совпадают.
Несколько проще обстоит дело с хрупкими и малопластичными материалами. Не внося существенной погрешности, можно считать, что они работают упруго вплоть до разрушения, иными словами, обладают линейной диаграммой деформирования. В этой ситуации для ее описания нет необходимости, как прежде, использовать истинное напряжение – достаточно условного, а логарифмическую пластическую деформацию вполне заменит обычное относительное удлинение:

(очевидно,показатель упрочнения m = 1).
Привлекая для определения постоянных а и b деформационного критерия в форме (15) данные испытаний на растяжение (см. выше), получим соотношение между ними, аналогичное (16),
 ;
;
с помощью результатов испытаний на сжатие – величину а:
 .
.
Разрушение любого материала в условиях равноосного объемного растяжения, как уже было сказано ранее, является бездеформационным – в соответствии с любым критерием текучести пластического деформирования материала не происходит. В этом случае деформационным критерием (кото-
рый, напомним, является критерием вязкого разрушения) прогнозируется бесконечно малая величина истинного сопротивления отрыву  (см. выражения (15) или (18)), что не соответствует действительности. В связи с этим обычно принимают
(см. выражения (15) или (18)), что не соответствует действительности. В связи с этим обычно принимают  .
.
При равноосном объемном сжатии ( ,
,  , s И = 0,
, s И = 0, 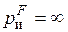 ) возможность разрушения критерием отрицается.
) возможность разрушения критерием отрицается.
Особенность деформационного критерия по сравнению с рассмотренными ранее состоит в том, что им отражается более существенное снижение прочности при двух- и трехосном растяжении и, в ряде случаев, наоборот, ее повышение при неодноосном сжатии. Более высоким получается также сопротивлению сдвигу (при малых значениях n F последний результат вызывает сомнения, к сожалению, соответствующие экспериментальные данные нам неизвестны, возможно, они отсутствуют).
Примеры поверхностей разрушения, построенных с помощью деформационного критерия для пластичного и хрупкого материалов в относительных координатах  , показаны на рис. 13, 14.
, показаны на рис. 13, 14.
Указание: в ПЗ помимо общих выражений также должны быть приведены расчетные критериальные зависимости, в которые подставлены конкретные для заданного материала значения постоянных (nF i,  ).
).




 к интенсивности напряжений s И (8). Таким образом, этот критерий вносит существенную поправку в формулировку гипотезы наибольших деформаций (14) – своего прямого исторического предшественника.
к интенсивности напряжений s И (8). Таким образом, этот критерий вносит существенную поправку в формулировку гипотезы наибольших деформаций (14) – своего прямого исторического предшественника. от отношения s 0/ s И(рис. 15)
от отношения s 0/ s И(рис. 15) * Сен-Венан, Адемар Жан-Клод Барре (1797 – 1886) – французский механик и инженер, один из основоположников сопротивления материалов, теории упругости и основ теории пластичности. Получил решение задач изгиба и кручения стержней. Изучал деформирование прямых и кривых (в том числе, пружин) стержней, чистый изгиб стержня за пределами упругости, удар и колебания балок. Читал лекции по механике в Школе мостов и дорог, Агроинженерном институте в Версале. С 1868 г. – действительный член Парижской академии наук.
* Сен-Венан, Адемар Жан-Клод Барре (1797 – 1886) – французский механик и инженер, один из основоположников сопротивления материалов, теории упругости и основ теории пластичности. Получил решение задач изгиба и кручения стержней. Изучал деформирование прямых и кривых (в том числе, пружин) стержней, чистый изгиб стержня за пределами упругости, удар и колебания балок. Читал лекции по механике в Школе мостов и дорог, Агроинженерном институте в Версале. С 1868 г. – действительный член Парижской академии наук.

 . (15)
. (15) ; тогда из формулы (15) следует, что эти две константы взаимосвязаны:
; тогда из формулы (15) следует, что эти две константы взаимосвязаны: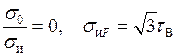 – получим
– получим . (17)
. (17) * Кононов, Константин Михайлович (1934 – 2001) – канд. техн. наук, доцент кафедры «Сопротивление материалов, динамика и прочность машин» ЧПИ – ЧГТУ – ЮУрГУ. Руководитель кафедрального отдела экспериментальных исследований, разработчик курса «Конструкционная прочность» для студентов специальности «Динамика и прочность машин». Соавтор трех монографий, около 80 научных статей и ряда учебных пособий.
* Кононов, Константин Михайлович (1934 – 2001) – канд. техн. наук, доцент кафедры «Сопротивление материалов, динамика и прочность машин» ЧПИ – ЧГТУ – ЮУрГУ. Руководитель кафедрального отдела экспериментальных исследований, разработчик курса «Конструкционная прочность» для студентов специальности «Динамика и прочность машин». Соавтор трех монографий, около 80 научных статей и ряда учебных пособий. (gpF – пластическая деформация сдвига в момент разрушения).
(gpF – пластическая деформация сдвига в момент разрушения). . (18)
. (18) ) можно найти предельную интенсивность напряжений s И F и соответствующую ей интенсивность деформаций для рассматриваемого материала (см. (7))
) можно найти предельную интенсивность напряжений s И F и соответствующую ей интенсивность деформаций для рассматриваемого материала (см. (7)) (19)
(19) .
. , из равенства (18) следует
, из равенства (18) следует ,
,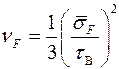 .
.
 ;
; .
. (см. выражения (15) или (18)), что не соответствует действительности. В связи с этим обычно принимают
(см. выражения (15) или (18)), что не соответствует действительности. В связи с этим обычно принимают  .
. ,
,  , s И = 0,
, s И = 0, 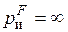 ) возможность разрушения критерием отрицается.
) возможность разрушения критерием отрицается. , показаны на рис. 13, 14.
, показаны на рис. 13, 14. ).
).


