ЛАБОРАТОРНЫЕ РАБОТЫ
по курсу физики
С компьютерными моделями
(МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА)
для студентов всех специальностей
всех форм обучения
МОСКВА – 2002
Ю.В.Тихомиров
Лабораторные работы по курсу физики с компьютерными моделями (молекулярная физика и термодинамика).
Учебное пособие для студентов высших технических учебных заведений дневной, вечерней и заочной (дистанционной) форм обучения.-М.:2002.- 27 с.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 4
1. ДОПУСК К ЛАБОРАТОРНОЙ РАБОТЕ. 6
2. ОФОРМЛЕНИЕ КОНСПЕКТА для ДОПУСКА к ЛАБОРАТОРНОЙ РАБОТЕ 6
3. ОФОРМЛЕНИЕ ЛАБОРАТОРНОЙ РАБОТЫ К ЗАЧЕТУ.. 7
4. МОЛЕКУЛЯРНАЯ ФИЗИКА и ТЕРМОДИНАМИКА.. 9
4_1 АДИАБАТИЧЕСКИЙ ПРОЦЕСС.. 9
4_2 РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА.. 14
4_3 ДИФФУЗИЯ В ГАЗАХ.. 18
4_4 УРАВНЕНИЕ СОСТОЯНИЯ ГАЗА ВАН-ДЕР-ВААЛЬСа. 22
3. ЛИТЕРАТУРА.. 26
4. НЕКОТОРЫЕ ПОЛЕЗНЫЕ СВЕДЕНИЯ.. 27
ВВЕДЕНИЕ
Данный сборник лабораторных работ с элементами компьютерного моделирования содержит описания к лабораторным работам, в которых используются компьютерные модели, разработанные фирмой «Физикон» в среде Windows и включенные в CD-ROM «Открытая физика 1.0» часть 1.
Работа в среде Windows 9Х требует определенных навыков и привычки оперировать с некоторыми стандартными для этой среды способами организации диалога компьютер-пользователь. Для запуска программы необходимо дважды щелкнуть левой кнопкой мыши, когда ее маркер расположен над эмблемой данной части сборника компьютерных моделей. После этого появится начальная картинка, имеющая вид

После этого необходимо дважды щелкнуть левой кнопкой мыши, установив ее маркер над названием радела, в котором расположена данная модель. Для Молекулярной физики и термодинамики вы увидите следующую картинку

Чтобы увидеть дальнейшие пункты содержания данного раздела надо щелкать левой кнопкой мыши, установив ее маркер на кнопку со стрелкой вниз, расположенную в правом нижнем углу внутреннего окна.
Кнопки вверху картинки являются служебными. Предназначение каждой проявляется когда маркер мыши располагается над нею в течение 1-2 секунд (без нажатия кнопок мыши). Очень важной является кнопка с двумя вертикальными чертами «çê», которая служит для остановки эксперимента, а рядом расположенные кнопки – для шага «u ç» и продолжения «uu» работы.
Прочитав надписи во внутреннем окне установите маркер мыши над надписью требуемой компьютерной модели и дважды коротко нажмите левую кнопку мыши. В появившемся внутреннем окне (смотри рисунок в описании к лабораторной работе на стр. 11) сверху также будут расположены служебные кнопки. Кнопка с изображением страницы служит для вызова теоретических сведений. Перемещать окна можно, зацепив (нажав и удерживая левую кнопку) мышью заголовок окна (имеющий синий фон). Закрытие окна теории обеспечивается нажатием кнопки с крестом в правом верхнем углу внутреннего окна.
ОФОРМЛЕНИЕ КОНСПЕКТА для ДОПУСКА к ЛАБОРАТОРНОЙ РАБОТЕ
Конспект для допуска к ЛР готовится заранее на двойных листах из школьной тетради в клетку (4-5 двойных листов в зависимости от почерка).
 Первая страница (обложка):
Первая страница (обложка):
| Допуск
| Измерения
| Установка
| Зачет
|
|
|
|
|
|
Лабораторная работа N__
Название: …
Выполнил:
студент группы _____
ФИО_______________
Дата выполнения: ____
Дата сдачи: __________
Следующие страницы:
|
ЧЕРНОВИК
(здесь и далее на этой стороне должны быть представлены все расчеты, включая расчетные формулы и подстановку числовых значений)
|
Цель работы: (переписать полностью из описания).
Краткая теория (выписать основные формулы и пояснить каждый символ, входящий в формулу).
Экспериментальная установка (нарисовать чертеж и написать наименование деталей).
Таблицы (состав таблиц и их количество определить самостоятельно в соответствии с методикой измерений и обработкой их результатов).
Оформление отчета (переписать полностью из описания). Этот раздел в описании может иметь и другое название, например, “Обработка результатов и оформление отчета”.
|
ОФОРМЛЕНИЕ ЛАБОРАТОРНОЙ РАБОТЫ К ЗАЧЕТУ
Полностью оформленная и подготовленная к зачету работа должна соответствовать следующим требованиям:
Выполнение всех пунктов раздела описания “Оформление отчета” (в черновике представлены все расчеты требуемых величин, заполнены чернилами все таблицы, построены все графики).
Графики должны удовлетворять всем требованиям, приведенным ниже.
Для всех величин в таблицах должна быть записана соответствующая единица измерения.
Записаны выводы по каждому графику (см. ниже шаблон)
Выписан ответ по установленной форме (см. ниже шаблон).
Записаны выводы по ответу (см. ниже шаблон).
Г Р А Ф И К (требования):
· на миллиметровке или листе в клетку, размер не менее 1/2 тетрадного листа,
· на графике: оси декартовой системы, на концах осей - стрелки, индексы величин, единицы измерения, 10N,
· на каждой оси - равномерный масштаб (риски через равные промежутки, числа через равное количество рисок),
· под графиком - полное название графика СЛОВАМИ,
· на графике - экспериментальные и теоретические точки ярко,
· форма графика соответствует теоретической зависимости (не ломаная).
ВЫВОД по ГРАФИКУ (шаблон):
Полученный экспериментально график зависимости __________________
название функции словами
от ______________ имеет вид прямой (проходящей через начало координат,
название аргумента
параболы, гиперболы, плавной кривой) и качественно совпадает с теорети-ческой зависимостью данных характеристик, имеющей вид ______________.
формула
ОТВЕТ: По результатам измерений и расчетов получено значение _________________________, равное _____ = (___ ± ____) 10 ___ _________
название физической характеристики символ среднее ошибка степень един.измер
ВЫВОД по ОТВЕТУ (шаблон):
Полученное экспериментально значение величины _________________,
полное название словами
равное _________________, с точностью до ошибки измерений,
число, единица измерения
составляющей ________________, совпадает (не совпадает) с табличным
число, единица измерения
(теоретическим) значением данной величины, равным ________________.
число, единица измерения
АДИАБАТИЧЕСКИЙ ПРОЦЕСС
Ознакомьтесь с теорией в конспекте и учебнике (Савельев, т.1, §82,97).
Выберите «Термодинамика и молекулярная физика», «Адиабатический процесс». Нажмите кнопку с изображением страницы во внутреннем окне. Прочитайте теорию и запишите необходимое в свой конспект лабораторной работы. Закройте окно теории, нажав кнопку с крестом в правом верхнем углу внутреннего окна.
ЦЕЛЬ РАБОТЫ:
* Знакомство с компьютерной моделью, описывающей адиабатический процесс в идеальном газе.
* Экспериментальное подтверждение закономерностей адиабатического процесса.
* Экспериментальное определение показателя адиабаты, количества степеней свободы и структуры молекул газа в данной модели.
КРАТКАЯ ТЕОРИЯ:
СОСТОЯНИЕ системы имеет фиксированные значения макроскопических параметров, описывающих систему в целом. Параметры, характеризующие систему в целом, называются ПАРАМЕТРАМИ СОСТОЯНИЯ. Примерами являются температура, давление, объем и т.д.
РАВНОВЕСНЫМ называется такое состояние системы, при котором все параметры системы имеют определенные значения, остающееся неизменными сколь угодно долго при неизменных внешних условиях.
ОБРАТИМЫМ называется процесс, при реализации которого в обратном направлении система проходит через те же состояния, что и при прямом ходе, но в обратной последовательности. Равновесные процессы всегда обратимы.
КРУГОВЫМ процессом (ЦИКЛОМ) называется процесс, при котором система после ряда изменений возвращается в исходное состояние.
УРАВНЕНИЕ СОСТОЯНИЯ идеального газа (уравнение Менделеева-Клапейрона)
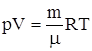 .
.
ТЕПЛОЕМКОСТЬ тела численно равна отношению количества тепла d’Q, сообщенного телу, к изменению температуры тела dT, которое при этом произошло:
СТЕЛА = 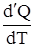 .
.
УДЕЛЬНОЙ теплоемкостью вещества называется отношение теплоемкости к массе тела.
Если тело нем меняет свой объем, то оно не совершает работы, поэтому при постоянном объеме тела переданное телу тепло dQ’ идет на изменение его внутренней энергии dU.
ТЕПЛОЕМКОСТЬ ПРИ ПОСТОЯННОМ ОБЪЕМЕ
СV =  .
.
ТЕПЛОЕМКОСТЬ ПРИ ПОСТОЯННОМ ДАВЛЕНИИ идеального газа, молекулы которого имеют i степеней свободы
CP = 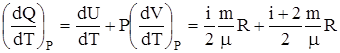 (1).
(1).
ОТНОШЕНИЕ 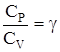 является константой (в определенном диапазоне температур) для данного газа. Эта константа называется показателем адиабаты.
является константой (в определенном диапазоне температур) для данного газа. Эта константа называется показателем адиабаты.
Формула 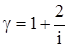 (2) устанавливает связь отношения теплоемкостей g с числом степеней свободы молекулы газа i.
(2) устанавливает связь отношения теплоемкостей g с числом степеней свободы молекулы газа i.
ЧИСЛО (количество) СТЕПЕНЕЙ СВОБОДЫ есть минимальное количество независимых координат, необходимых для однозначного описания положения молекулы в пространстве ИЛИ минимальное количество независимых движений, суперпозиция которых дает любое движение молекулы.
ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ всегда дает 3 степени свободы.
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ дает 2 степени свободы для линейной молекулы и 3 степени свободы, если атомы в молекуле не расположены на одной линии.
КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ дает 2nКОЛ степеней свободы, где nКОЛ – количество независимых колебаний атомов в молекуле (у двухатомной молекулы nКОЛ = 1).
АДИАБАТИЧЕСКИМ называется процесс, происходящий без теплообмена с внешней средой (d’Q = 0). Уравнение адиабаты
PVg = const (3).
Принято также выделять ИЗОТЕРМИЧЕСКИЙ, ИЗОБАРИЧЕСКИЙ и ИЗОХОРИЧЕСКИЙ процессы.
МЕТОДИКА и ПОРЯДОК ИЗМЕРЕНИЙ
Внимательно рассмотрите картинку на рисунке, найдите рисунок элемента, в котором реализуется адиабатический процесс, обратите внимание на его теплоизоляцию. Найдите математическую формулировку условия теплоизоляции. Ознакомьтесь с графиками в правой части изображения.
Зарисуйте необходимое в свой конспект лабораторной работы.
РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА
Ознакомьтесь с теорией в конспекте и учебнике (Савельев, т.1, §93,98,99).
Выберите «Термодинамика и молекулярная физика», «Распределение Максвелла». Нажмите кнопку с изображением страницы во внутреннем окне. Прочитайте теорию и запишите необходимое в свой конспект лабораторной работы. Закройте окно теории, нажав кнопку с крестом в правом верхнем углу внутреннего окна.
ЦЕЛЬ РАБОТЫ:
* Знакомство с компьютерной моделью, описывающей поведение молекул идеального газа
* Экспериментальное подтверждение распределения Максвелла молекул идеального газа по скоростям.
* Экспериментальное определение массы молекул в данной модели.
КРАТКАЯ ТЕОРИЯ:
ВЕРОЯТНОСТЬЮ Рi получения некоторого результата измерения называется предел отношения количества измерений, давших этот результат, (Ni) к полному числу измерений N, когда N ® ¥.
ЭЛЕМЕНТАРНОЙ вероятностью dPV при измерении величины скорости v называется вероятность наличия скорости величиной от v до v + dv. Эта вероятность пропорциональна приращению скорости dv: dPV = F(v) dv, где коэффициент пропорциональности F(v) называется ФУНКЦИЕЙ РАСПРЕДЕЛЕНИЯ молекул по величине скорости. Она может быть выражена через другие функции распределения
F(v) = j(vX)×j(vY)×j(vZ)×4pv2 = f(v)×4pv2, где j(vX), ×j(vY) и×j(vZ) - функции распределения для соответствующих проекций скоростей молекул, а f(v) - их произведение.
В §98 вы можете найти вывод формул, в частности
 .
.
СреднЯЯ скорость 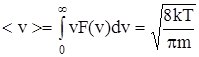 ,
,
СреднЯЯ квадратичная скорость vср.кв =  .
.
Наивероятнейшей называется скорость vВЕР, при которой F(v) имеет максимум:
vВЕР =  .
.
Табличные значения
| Газ
| Водород
| Гелий
| Неон
| Азот
| Кислород
|
| Масса молекулы 10-27 кг
| 3.32
| 6.64
| 33.2
| 46.5
| 53.12
|
Вопросы и задания для самоконтроля
1. Дайте определение вероятности получения некоторого результата измерения.
2. Дайте определение элементарной вероятности при измерении величины скорости.
3. Что такое функция распределения?
4. Как связаны функции распределения величины и проекции скорости?
5. Каковы особенности графика функции распределения величины скорости молекул идеального газа?
6. Как вычисляется среднее значение некоторой физической величины А, если известна ее функция распределения f(A)?
7. Напишите формулу для вычисления среднего значения скорости молекул.
8. Напишите формулу для вычисления средней квадратичной скорости молекул.
9. Напишите условие для вычисления наивероятнейшей скорости молекул.
10. Напишите выражение для средней скорости молекул идеального газа.
11. Напишите выражение для средней квадратичной скорости молекул идеального газа.
12. Напишите выражение для наивероятнейшей скорости молекул идеального газа.
13. Вычислите на сколько процентов отличаются средняя и средняя квадратичная скорости молекул идеального газа.
14. Вычислите на сколько процентов отличаются средняя и наивероятнейшая скорости молекул идеального газа.
ЛАБОРАТОРНАЯ РАБОТА № 4_3
ДИФФУЗИЯ В ГАЗАХ
Ознакомьтесь с теорией в конспекте и учебнике (Савельев, т.1, §128, §130).
Выберите «Термодинамика и молекулярная физика», «Диффузия». Нажмите кнопку с изображением страницы во внутреннем окне. Прочитайте теорию и запишите необходимое в свой конспект лабораторной работы. Закройте окно теории, нажав кнопку с крестом в правом верхнем углу внутреннего окна.
ЦЕЛЬ РАБОТЫ:
* Знакомство с компьютерной моделью, описывающей диффузию молекул идеального газа
* Экспериментальное подтверждение закона диффузии.
* Экспериментальное определение средней скорости теплового движения частиц в данной модели.
КРАТКАЯ ТЕОРИЯ:
При нарушении равновесия макросистема стремится вернуться в равновесное состояние.
ЯВЛЕНИЯМИ ПЕРЕНОСА называются процессы, связанные с возникновением в веществе НАПРАВЛЕННОГО ПЕРЕНОСА (потока) массы, импульса или внутренней энергии.
ДИФФУЗИЯ есть процесс установления внутри фаз вещества равновесного распределения концентраций, который обеспечивается направленным переносом массы этого вещества. Диффузия обусловлена тепловым движением молекул и проявляется в самопроизвольном выравнивании концентраций в смеси нескольких веществ.
САМОДИФФУЗИЯ имеет место при самопроизвольном выравнивании концентрации однородного вещества, если по некоторым причинам равновесное распределение концентрации было нарушено.
ДЛИНА СВОБОДНОГО ПРОБЕГА l есть среднее расстояние, пролетаемое частицей между двумя последовательными столкновениями. Эффективный диаметр частицы есть минимальное расстояние, на которое сближаются центры двух сталкивающихся частиц.
Если в начальный момент времени имеет место неоднородное распределение плотности вещества r вдоль только одной оси (например, ОХ), тогда возникает одномерная диффузия, связанная с переносом массы М вдоль этой оси ОХ. Для двухкомпонентной системы (например, смеси двух газов) одномерная диффузия описывается первым законом Фика:

где dM - масса одного компонента (индексы для характеристик данного компонента пропущены), которая переносится за время dt через элементарную площадку, перпендикулярную оси ОХ, имеющую площадь dS, в направлении убывания плотности этого компонента,  градиент плотности первого компонента, D - коэффициент диффузии.
градиент плотности первого компонента, D - коэффициент диффузии.
Для смеси «красных» и «зеленых» частиц, имеющих одинаковую массу m каждой частицы, dM = m·dN, r = m  , а
, а  , где dN - количество частиц, проходящих через dS за время dt, которое равно
, где dN - количество частиц, проходящих через dS за время dt, которое равно  , где разность числа частиц в левом и правом сосудах DN = N2 - N1 , N2 = N0 - N(t), N1 = N(t), DX = Lотв, объем сосуда V = 20 cм3, dS есть площадь отверстия. Решаем уравнение методом разделения переменных:
, где разность числа частиц в левом и правом сосудах DN = N2 - N1 , N2 = N0 - N(t), N1 = N(t), DX = Lотв, объем сосуда V = 20 cм3, dS есть площадь отверстия. Решаем уравнение методом разделения переменных:
 . Интегрируем слева от 0 до N(t), а справа - от 0 до t и получаем:
. Интегрируем слева от 0 до N(t), а справа - от 0 до t и получаем:
 или
или  .
.
ТАБЛИЦА 1. Значения диаметров соединительной трубки, длительности промежутка измерения и сорта частиц.
| Бригада
|
|
|
|
|
|
|
|
|
| d1, мм
|
|
|
|
|
|
|
|
|
| d2, мм
|
|
|
|
|
|
|
|
|
| Dt, с
|
|
|
|
|
|
|
|
|
| Сорт
| красн
| зелен
| красн
| зелен
| красн
| зелен
| красн
| зелен
|
| Объем
| справа
| слева
| справа
| слева
| справа
| слева
| справа
| слева
|
ОБРАЗЕЦ ТАБЛИЦ 2,3 для записи результатов:
| t[с]=
| Dt
| 2Dt
| 3Dt
| 4Dt
| 5Dt
| 6Dt
| 7Dt
| 8Dt
| 9Dt
| 10Dt
|
| N(t)=
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА:
Вычислите и запишите в таблицы все указанные значения.
Постройте на одном рисунке графики экспериментальных зависимостей
-  = f(t) и, используя формулу D =
= f(t) и, используя формулу D =  , определите по графикам коэффициенты диффузии для каждого отверстия. Длину отверстия Lотв измерьте линейкой на экране монитора, объем сосуда V = 20 см3.
, определите по графикам коэффициенты диффузии для каждого отверстия. Длину отверстия Lотв измерьте линейкой на экране монитора, объем сосуда V = 20 см3.
Найдите среднее значение коэффициента диффузии и, используя соотношение  , найдите среднюю скорость теплового движения vср частиц (lср = 2 см).
, найдите среднюю скорость теплового движения vср частиц (lср = 2 см).
Сделайте выводы по графику и ответу. В выводе по ответу сравните полученное экспериментально значение vср с величиной скорости, оцененной «на глаз».
Вопросы и задания для самоконтроля
1. Что происходит с макросистемой при нарушении равновесия?
2. Дайте определение явления переноса.
3. Назовите примеры явлений переноса.
4. Дайте определение явления диффузии.
5. Чем обусловлена диффузия?
6. В чем проявляется диффузия?
7. Какая диффузия называется одномерной?
8. Что такое самодиффузия?
9. Напишите уравнение одномерной диффузии для двухкомпонентной системы газов.
10. Каков физический смысл коэффициента диффузии.
11. Что такое плотность тела?
12. Что такое концентрация молекул (частиц)?
13. Дайте определение градиента плотности в общем случае.
14. Напишите формулу для градиента плотности, если она меняется только вдоль оси ОХ.
15. Напишите формулу для градиента плотности, если она меняется только вдоль оси ОY.
16. Напишите формулу для градиента плотности, если она меняется только вдоль оси ОZ.
17. Напишите формулу для градиента плотности, если она меняется вдоль осей ОХ и OY.
18. Что такое длина свободного пробега частицы?
19. Что такое эффективный диаметр и эффективное сечение частицы?
20. Какое уравнение связывает среднюю скорость с коэффициентом диффузии?
ЛАБОРАТОРНАЯ РАБОТА № 4_4
ЦЕЛЬ РАБОТЫ:
* Знакомство с компьютерной моделью, описывающей вещество в газообразном состоянии и его переход в жидкое состояние.
* Экспериментальное подтверждение закономерностей поведения реального газа.
КРАТКАЯ ТЕОРИЯ:
ФИЗИЧЕСКИМ газом называется вещество, находящееся в газообразном состоянии.
«идеальный газ» это название модели, описывающей физический газ, находящийся в сильно разреженном состоянии (при не слишком больших давлениях и достаточно высоких температурах). Уравнением, связывающим параметры состояния идеального газа, является уравнение Менделеева-Клапейрона. Поэтому оно имеет второе название: уравнение состояния идеального газа. Его вид известен: pV = nRT, где p - давление газа, V - объем газа, n - количество киломолей, R - универсальная газовая постоянная, T - температура газа.
Более точная модель физического (реального) газа была предложена Ван-дер-Ваальсом. Она также является приближенной, но лучше описывает процессы, нежели модель «идеальный газ». Иногда эту модель называют «реальный газ». Газом Ван-дер-ваальса (ВдВ) называется воображаемый газ (модель), параметры состояния которого точно подчиняются уравнению
 .
.
Оно называется УРАВНЕНИЕМ ВАН-ДЕР-ВААЛЬСА. Здесь a и b - константы Ван-дер-Ваальса.
Добавка к внешнему давлению (а) обусловлена взаимным притяжением молекул друг к другу.
Поправка к объему (b) характеризует ту часть объема, которая недоступна для движения молекул. Она равна нескольким суммарным объемам молекул, содержащихся в газе.
ИЗОТЕРМОЙ называется зависимость давления от объема данного (фиксированного) количества вещества при постоянной температуре.
На рис.1 приведены изотермы некоторого физического (реального) газа, а на рис.2 и рис.3 - изотермы ВдВ газа (взяты из учебника [1]).
Изотерма ВдВ газа, имеющая только точку перегиба и не имеющая экстремумов, называется критической. Температура критической изотермы называется критической температурой. Объем и давление в критической точке также называются КРИТИЧЕСКИМИ.
УРАВНЕНИЯ ДЛЯ КРИТИЧЕСКИХ ПАРАМЕТРОВ:
VКР = 3b, pКР =  , TКР =
, TКР =  . Отсюда А =
. Отсюда А =  n = 0.375n.
n = 0.375n.
При температуре выше критической вещество может находиться только в газообразном состоянии. При температуре ниже критической вещество может находиться как в газообразном, так и в жидком состоянии.
Жидкое состояние описывается левыми (по отношению к точке перегиба) частями графиков на рисунках и характерно тем, что небольшое уменьшение объема вещества может произойти только при резком увеличении давления (жидкость практически несжимаема).
Изотермы ВдВ примерно совпадают с изотермами реального газа на участках, соответствующих однофазным состояниям вещества.
Рис.3 разъясняет поведение вещества при разных внешних условиях. В области, где присутствуют 2 фазы (1-2-3-4) S-образный завиток изотермы ВдВ заменяется горизонтальным участком (1-4) реальной изотермы (см.учебник).
НЕРЕАЛИЗУЕМОЕ СОСТОЯНИЕ соответствует участку 2-3, на котором сжимаемость  вещества была бы отрицательна, что невозможно.
вещества была бы отрицательна, что невозможно.
ПЕРЕОХЛАЖДЕННЫЙ ПАР на участке 3-4 реализуется при определенных условиях (при практическом отсутствии центров конденсации и внешних воздействий).
ПЕРЕГРЕТАЯ ЖИДКОСТЬ на участке 1-2 реализуется при отсутствии примесей, способных быть центрами кипения.
ИЗМЕРЕНИЯ
ЭКСПЕРИМЕНТ 1. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ ПАРАМЕТРОВ
Щелкните левой кнопкой мыши, когда ее маркер на кнопке «Выбор».
Подведите маркер мыши к кнопке у верхней границы столбика на регуляторе температуры и нажмите левую кнопку мыши. Удерживая кнопку в нажатом состоянии, перемещайте границу столбика до тех пор, пока на правом экране не появится критическая изотерма с точкой перегиба и без экстремумов.
Запишите в свой конспект значения критических параметров ТКР, VКР, pКР.
ЭКСПЕРИМЕНТ 2. ИССЛЕДОВАНИЕ ИЗОТЕРМ ГАЗА ВдВ.
1.Установите значение температуры, указанное первым в таблице начальных значений для вашей бригады. Нажмите мышью кнопку «СТАРТ» на экране и наблюдайте перемещение поршня на левой картинке модели и перемещение точки по красной кривой теоретической адиабаты. Попробуйте останавливать процесс нажатием кнопки «Стоп» на экране. Последующий запуск процесса осуществляется нажатием кнопки «Старт».
После остановки процесса запустите его снова, нажав кнопку «Старт», и останавливайте, нажимая кнопку «Стоп», когда крестик на теоретической изотерме (красная кривая) будет находиться вблизи следующих значений объема: 0.1, 0.12, 0.14, 0.16, 0.18 и 0.2 дм3 (6 значений), записывая при остановке значения в таблицу 2.
Установив новое значение температуры Т из таблицы 1, задавая Vнач = 0.1 дм3, повторите измерения, записывая результаты в таблицы 3,4,5.
ТАБЛИЦА 1. Примерные значения температуры (не перерисовывать)
ТАБЛИЦЫ 2,3,4,5 Результаты измерений при Т = ____ К
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА:
По измеренным значениям критических параметров вычислите константу
А =  .
.
Постройте на одном рисунке графики экспериментальных зависимостей давления от обратного объема для начальных точек всех изотермических процессов (указав на них температуры).
Для каждой изотермы определите значение количества вещества, используя  .
.
Вычислите среднее значение n и величину константы А’ по формуле А’ = 0.375n. Запишите ответ для А’ и проанализируйте ответы и графики. В выводах по ответу сравните А’, полученное по изотермам, с А, полученным через критические параметры.
Вопросы и задания для самоконтроля
1. Что такое физический газ?
2. Перечислите все известные агрегатные состояния вещества.
3. Что такое идеальный газ?
4. При каких условиях физический газ можно описывать моделью идеальный газ?
5. Что такое уравнение состояния?
6. Как выглядит уравнение состояния идеального газа? Каково его второе название?
7. Что такое газ Ван-дер-Ваальса?
8. Как выглядит уравнение состояния газа Ван-дер-Ваальса? Каково его второе название?
9. Что такое константы Ван-дер-Ваальса?
10. Что определяет первая константа Ван-дер-Ваальса?
11. Что определяет вторая константа Ван-дер-Ваальса?
12. Что такое изотерма?
13. Что такое критическая изотерма?
14. Каковы особенности поведения газа при температуре, выше критической?
15. Каковы особенности поведения газа при температуре, ниже критической?
16. На каких участках изотермы ВдВ примерно совпадают с изотермами реального газа?
ЛИТЕРАТУРА
1. Савельев И.В. Курс общей физики. Т.1. М.: «Наука», 1982.
2. Савельев И.В. Курс общей физики. Т.2. М.: «Наука», 1978.
3. Савельев И.В. Курс общей физики. Т.3. М.: «Наука», 1979.
НЕКОТОРЫЕ ПОЛЕЗНЫЕ СВЕДЕНИЯ
ФИЗИЧЕСКИЕ КОНСТАНТЫ
| Название
| Символ
| Значение
| Размерность
|
| Гравитационная постоянная
| g или G
| 6.67 10-11
| Н м2кг-2
|
| Ускорение свободного падения на поверхности Земли
| g0
| 9.8
| м с-2
|
| Скорость света в вакууме
| c
| 3 108
| м с-1
|
| Постоянная Авогадро
| NA
| 6.02 1026
| кмоль-1
|
| Универсальная газовая постоянная
| R
| 8.31 103
| Дж кмоль-1 К-1
|
| Постоянная Больцмана
| k
| 1.38 10-23
| Дж К-1
|
| Элементарный заряд
| e
| 1.6 10-19
| Кл
|
| Масса электрона
| me
| 9.11 10-31
| кг
|
| Постоянная Фарадея
| F
| 9.65 104
| Кл моль-1
|
| Электрическая постоянная
| eо
| 8.85 10-12
| Ф м-1
|
| Магнитная постоянная
| mо
| 4p 10-7
| Гн м-1
|
| Постоянная Планка
| h
| 6.62 10-34
| Дж с
|
ПРИСТАВКИ И МНОЖИТЕЛИ
для образования десятичных кратных и дольных единиц
| Приставка
| Символ
| Множитель
|
| Приставка
| Символ
| Множитель
|
|
|
| дека
| да
| 101
|
| деци
| д
| 10-1
|
| гекто
| г
| 102
|
| санти
| с
| 10-2
|
| кило
| к
| 103
|
| милли
| м
| 10-3
|
| мега
| М
| 106
|
| микро
| мк
| 10-6
|
| гига
| Г
| 109
|
| нано
| н
| 10-9
|
| тера
| Т
| 1012
|
| пико
| п
| 10-12
|
ЛАБОРАТОРНЫЕ РАБОТЫ
по курсу физики
С компьютерными моделями
(МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА)
для студентов всех специальностей
всех форм обучения
МОСКВА – 2002
Ю.В.Тихомиров
Лабораторные работы по курсу физики с компьютерными моделями (молекулярная физика и термодинамика).
Учебное пособие для студентов высших технических учебных заведений дневной, вечерней и заочной (дистанционной) форм обучения.-М.:2002.- 27 с.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 4
1. ДОПУСК К ЛАБОРАТОРНОЙ РАБОТЕ. 6
2. ОФОРМЛЕНИЕ КОНСПЕКТА для ДОПУСКА к ЛАБОРАТОРНОЙ РАБОТЕ 6
3. ОФОРМЛЕНИЕ ЛАБОРАТОРНОЙ РАБОТЫ К ЗАЧЕТУ.. 7
4. МОЛЕКУЛЯРНАЯ ФИЗИКА и ТЕРМОДИНАМИКА.. 9
4_1 АДИАБАТИЧЕСКИЙ ПРОЦЕСС.. 9
4_2 РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА.. 14
4_3 ДИФФУЗИЯ В ГАЗАХ.. 18
4_4 УРАВНЕНИЕ СОСТОЯНИЯ ГАЗА ВАН-ДЕР-ВААЛЬСа. 22
3. ЛИТЕРАТУРА.. 26
4. НЕКОТОРЫЕ ПОЛЕЗНЫЕ СВЕДЕНИЯ.. 27
ВВЕДЕНИЕ
Данный сборник лабораторных работ с элементами компьютерного моделирования содержит описания к лабораторным работам, в которых используются компьютерные модели, разработанные фирмой «Физикон» в среде Windows и включенные в CD-ROM «Открытая физика 1.0» часть 1.
Работа в среде Windows 9Х требует определенных навыков и привычки оперировать с некоторыми стандартными для этой среды способами организации диалога компьютер-пользователь. Для запуска программы необходимо дважды щелкнуть левой кнопкой мыши, когда ее маркер расположен над эмблемой данной части сборника компьютерных моделей. После этого появится начальная картинка, имеющая вид

После этого необходимо дважды щелкнуть левой кнопкой мыши, установив ее маркер над названием радела, в котором расположена данная модель. Для Молекулярной физики и термодинамики вы увидите следующую картинку

Чтобы увидеть дальнейшие пункты содержания данного раздела надо щелкать левой кнопкой мыши, установив ее маркер на кнопку со стрелкой вниз, расположенную в правом нижнем углу внутреннего окна.
Кнопки вверху картинки являются служебными. Предназначение каждой проявляется когда маркер мыши располагается над нею в течение 1-2 секунд (без нажатия кнопок мыши). Очень важной является кнопка с двумя вертикальными чертами «çê», которая служит для остановки эксперимента, а рядом расположенные кнопки – для шага «u ç» и продолжения «uu» работы.
Прочитав надписи во внутреннем окне установите маркер мыши над надписью требуемой компьютерной модели и дважды коротко нажмите левую кнопку мыши. В появившемся внутреннем окне (смотри рисунок в описании к лабораторной работе на стр. 11) сверху также будут расположены служебные кнопки. Кнопка с изображением страницы служит для вызова теоретических сведений. Перемещать окна можно, зацепив (нажав и удерживая левую кнопку) мышью заголовок окна (имеющий синий фон). Закрытие окна теории обеспечивается нажатием кнопки с крестом в правом верхнем углу внутреннего окна.
ДОПУСК К ЛАБОРАТОРНОЙ РАБОТЕ
Для допуска:
* Каждый студент предварительно оформляет свой персональный конспект данной ЛР (см. соответствующие требования).
* Преподаватель индивидуально проверяет оформление конспекта и задает вопросы по теории, методике измерений, установке и обработке результатов.
* Студент отвечает на заданные вопросы (письменно в черновике конспекта или устно).
* Преподаватель допускает студента к работе и ставит свою подпись в конспекте студента (графа ДОПУСК в табличке на обложке).
ОФОРМЛЕНИЕ КОНСПЕКТА для ДОПУСКА к ЛАБОРАТОРНОЙ РАБОТЕ
Конспект для допуска к ЛР готовится заранее на двойных листах из школьной тетради в клетку (4-5 двойных листов в зависимости от почерка).
 Первая страница (обложка):
Первая страница (обложка):
| Допуск
| Измерения
| Установка
| Зачет
|
|
|
|
|
|
Лабораторная работа N__
Название: …





 Первая страница (обложка):
Первая страница (обложка):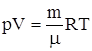 .
.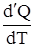 .
. .
.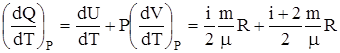 (1).
(1).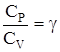 является константой (в определенном диапазоне температур) для данного газа. Эта константа называется показателем адиабаты.
является константой (в определенном диапазоне температур) для данного газа. Эта константа называется показателем адиабаты.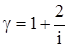 (2) устанавливает связь отношения теплоемкостей g с числом степеней свободы молекулы газа i.
(2) устанавливает связь отношения теплоемкостей g с числом степеней свободы молекулы газа i. .
.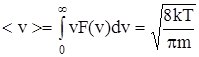 ,
, .
. .
.
 градиент плотности первого компонента, D - коэффициент диффузии.
градиент плотности первого компонента, D - коэффициент диффузии. , а
, а  , где dN - количество частиц, проходящих через dS за время dt, которое равно
, где dN - количество частиц, проходящих через dS за время dt, которое равно  , где разность числа частиц в левом и правом сосудах DN = N2 - N1 , N2 = N0 - N(t), N1 = N(t), DX = Lотв, объем сосуда V = 20 cм3, dS есть площадь отверстия. Решаем уравнение методом разделения переменных:
, где разность числа частиц в левом и правом сосудах DN = N2 - N1 , N2 = N0 - N(t), N1 = N(t), DX = Lотв, объем сосуда V = 20 cм3, dS есть площадь отверстия. Решаем уравнение методом разделения переменных: . Интегрируем слева от 0 до N(t), а справа - от 0 до t и получаем:
. Интегрируем слева от 0 до N(t), а справа - от 0 до t и получаем: или
или  .
.

 , определите по графикам коэффициенты диффузии для каждого отверстия. Длину отверстия Lотв измерьте линейкой на экране монитора, объем сосуда V = 20 см3.
, определите по графикам коэффициенты диффузии для каждого отверстия. Длину отверстия Lотв измерьте линейкой на экране монитора, объем сосуда V = 20 см3. , найдите среднюю скорость теплового движения vср частиц (lср = 2 см).
, найдите среднюю скорость теплового движения vср частиц (lср = 2 см). .
. Рис.1
Рис.1
 Рис.2
Рис.2
 Рис.3
Рис.3
 , TКР =
, TКР =  . Отсюда А =
. Отсюда А =  n = 0.375n.
n = 0.375n. вещества была бы отрицательна, что невозможно.
вещества была бы отрицательна, что невозможно. .
. .
.


