Рассмотрим решение линейного неравенства
a11х1+а12х2≤ b1 (18)
Так как строгое равенство представляет собой уравнение прямой, то множество решений неравенства (18) является одной из двух полуплоскостей на которые вся плоскость делится прямой а11х1+а12х2≤в1, включая и эту прямую, а другая полуплоскость с той же прямой есть множество решений неравенства с противоположным знаком:
а11х1+а12х2≥ b1 (19)
Для определения искомой полуплоскости задают произвольную контрольную точку, не лежащую на ее границе, т.е. не являющуюся решением уравнения. Если неравенство верно в той точке, то оно выполняется и во всех точках полуплоскости, содержащей контрольную точку, и не выполняется в точках другой полуплоскости.
Рассуждал аналогично, легко заметить, что множеством решений системы линейных неравенств с двумя переменными
а11х1+а12х2≤ b1 (20)
а11х1+а12х2≤ b2
…………………
am1х1+аm2х2≤ bm
является пересечением полуплоскостей.
В случае совместности системы это множество является выпуклым многоугольником или выпуклой многоугольной областью, содержащей конечное число угловых точек.
Напомним, что множество точек называется выпуклым, если для любых двух точек множества ему принадлежит и весь отрезок, соединяющий эти точки.
В частных (выраженных) случаях в качестве множества решений может быть луч, отрезок, единственная точка. В случае несовместности ограничений системы ее решением будет пустое множество.
Пример
Построить множество решений неравенства:
а) 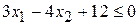 ; б)
; б)  .
.
Решение. В соответствии с теоремой 48.3.1, множество решений неравенства есть полуплоскость.
а) Построим границу полуплоскости − прямую 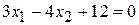 , найдя точки ее пересечения с осями координат
, найдя точки ее пересечения с осями координат 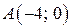 и
и  на рис. 1, а.
на рис. 1, а.
Для определения искомой полуплоскости (верхней или нижней) рекомендуется задать произвольную контрольную точку, не лежащую на ее границе − построенной прямой. Если неравенство выполняется в контрольной точке, то оно выполняется и во всех точках полуплоскости, содержащей контрольную точку, и не выполняется во всех точках другой полуплоскости.
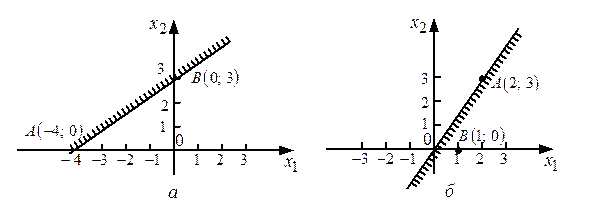
Рис. 1
И наоборот, в случае невыполнения неравенства в контрольной точке, оно не выполняется во всех точках полуплоскости, содержащей контрольную точку, и выполняется во всех точках другой полуплоскости.
В качестве контрольной точки удобно взять начало координат  , не лежащее на построенной прямой. Координаты точки
, не лежащее на построенной прямой. Координаты точки 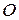 не удовлетворяют неравенству:
не удовлетворяют неравенству: 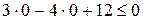 , следовательно, решением данного неравенства является нижняя полуплоскость, не содержащая контрольную точку
, следовательно, решением данного неравенства является нижняя полуплоскость, не содержащая контрольную точку 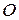 . Искомая полуплоскость выделена штриховкой.
. Искомая полуплоскость выделена штриховкой.
б) Построим границу полуплоскости − прямую  по двум точкам. Одной из этих точек является начало координат на рис. 1, б (в уравнении прямой отсутствует свободный член), а другую точку берем на прямой произвольно, например,
по двум точкам. Одной из этих точек является начало координат на рис. 1, б (в уравнении прямой отсутствует свободный член), а другую точку берем на прямой произвольно, например, 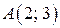 на рис. 1, б. В качестве контрольной возьмем, например, точку
на рис. 1, б. В качестве контрольной возьмем, например, точку 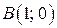 . Самую "простую" точку
. Самую "простую" точку  здесь в качестве контрольной брать не следует, ибо она лежит на построенной прямой. Так как координаты контрольной точки
здесь в качестве контрольной брать не следует, ибо она лежит на построенной прямой. Так как координаты контрольной точки 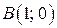 удовлетворяют неравенству, т.е.
удовлетворяют неравенству, т.е. 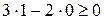 , то решением данного неравенства является нижняя (правая) полуплоскость, содержащая эту точку.
, то решением данного неравенства является нижняя (правая) полуплоскость, содержащая эту точку.
Вопросы для самостоятельной работы
Базовый уровень:
- Какие переменные в системе уравнений называются основными, свободными?
- Что называется базисным решением системы?
- Какое множество точек называется выпуклым?
- Какие множества на плоскости описываются линейными неравенствами?
- Какие переменные в системе уравнений называются базисными?
- В каких точках множества ограничений следует искать допустимые базисные решения системы линейных уравнений?
Повышенный уровень:
1. Решить системы уравнений по правилу Крамера, матричным способом и методом Жордана-Гаусса.:
| 1.81.
x1 – 2x2 + x3 = 1,
2x1 + 3x2 – x3 = 8,
x1 – x2 + 2x3 = –1.
| 1.82.
2x1 – x2 + 3x3 = 1,
x1 – 2x2 – 5x3 = –9,
4x1 + 3x2 – 2x3 = 4.
|
| 1.83.
2x1 – 3x2 + 4x3 = 20,
3x1 + 4x2 – 2x3 = –11,
4x1 + 2x2 + 3x3 = 9.
| 1.84.
4x1 – x2 + 3x3 = 1,
3x1 + 2x2 + 4x3 = 8,
2x1 – 2x2 + 4x3 = 0.
|
| 1.85.
10x1 – 7x2 = 7,
–3x1 + 2x2 + 6x3 = 4,
5x1 – x2 + 5x3 = 6.
| 1.86.
2x1 + 7x2 + 13x3 = 0,
3x1 + 14x2 – 12x3 = 8,
5x1 + 25x2 + 16x3 =39.
|
| 1.87.
2x1 + 4x2 – 3x3 = 2,
x1 + x2 + 2x3 = 0,
3x1 – 2x2 + x3 = –5.
| 1.88.
2x1 – 3x2 + x3 = 2,
x1 + 5x2 – 4x3 = –5,
4x1 + x2 – 3x3 = – 4.
|
| 1.89.
x1 + x2 – 3x3 = 0,
3x1 + 2x2 – 2x3 = –1,
x1 – x2 + 5x3 = –2.
| 1.90.
2x1 + 6x2 – x3 = 7,
4x1 – x2 + x3 = 4,
x1 + 2x2 – 3x3 = 0.
|
| 1.91.
x + 2y – 3z = 1,
2x – 3y – z = –7,
4x + y – 2z = 0.
| 1.92.
2x + 3y + z = 1,
x + y – 4z = 0,
4x + 5y – 3z =1.
|
| 1.93.
3x – y + 4z = 2,
x + 2y + 3z = 7,
5x + 3y + 2z = 8.
| 1.94.
3x – 2y – z = –5,
x + 3y +2z = 2,
5x – 2y + 4z = –7.
|
| 1.95.
4x + 2y – z = 0,
x + 2y + z = 1,
y – z = –3.
| 1.96.
2x – y = –1,
x + 2y – z = –2,
y + z = –2.
|
| 1.97.
2x – y + 5z = 4,
3x – y + 5z = 0,
5x + 2y + 13z = 2.
| 1.98.
x – 2y – z = –2,
2x – y = –1,
y + z = –2.
|
| 1.99.
3x + 2y – 4z = 8,
2x + 4y – 5z = 11,
4x – 3y + 2z = 1.
| 1.100.
2x – y + 4z = 15,
3x – y + z =8,
–2x + y + z = 0.
|
| 1.101.
4x + 2y – z = 0,
x + 2y + z = 1,
y – z = –3.
| 1.102.
2x – y = –1,
x + 2y – z = –2,
y + z = –2.
|
| 1.103.
2x – y + 5z = 4,
3x – y + 5z = 0,
5x + 2y +13z = 2.
| 1.104.
x – 2y – z = –2,
2x – y = –1,
y + z = –2.
|
| 1.105.
x – 4y + 3z = –22,
2x + 3y + 5z = 12,
3x – y – 2z = 0.
| 1.106.
x + 2y – 3z = 0,
2x – y + 4z = 5,
3x + y – z = 2.
|
| 1.107.
3x – 3y +2z = 2,
4x – 5y + 2z = 1,
5x – 6y + 4z = 3.
| 1.108.
3x + 2y – 4z = 8,
2x + 4y – 5z = 11,
4x – 3y + 2z = 1.
|
| 1.109.
x + y + z = 1,
x – y + 2z = –5,
4x + y + 4z = –2.
| 1.110.
2x – y + 4z = 15,
3x – y + z = 8,
–2x + y + z =0.
|
2. Исследовать совместность и найти общее решение следующих систем:
| 1.111.
3x1 – x2 + 5x3 – x4 = –3,
2x1 + 3x2 – x3 + x4 = 5,
x1 + x2 – 3x3 = 1,
4x1 + 2x2 – 18x3 + x4 = 4.
| 1.112.
3x1 – x2 + 4x3 + x4 = 1,
4x1 + x2 + x3 + 6x4 = –11,
2x1 + 3x2 –10x3 + 3x4 = 9.
|
| 1.113.
9x1 + 3x2 – x3 + x4 = 8,
6x1 – 2x2 + x3 – x4 = 6,
x1 – 3x2 + 7x3 + 2x4 = 8.
| 1.114.
2x1 + 2x2 – x3 + 7x4 = 3,
3x1 – x2 + 3x3 – 16x4 = 5,
4x1 + x2 – 5x3 + x4 = 0.
|
| 1.115.
x1 + 2x2 + 3x3 – x4 + x5 = 8,
2x1 – 2x2 + x3 – x4 + 3x5 = 6,
x1 – 4x2 + 3x3 + x4 – x5 = 2.
| 1.116.
x1 – 2x2 + 3x3 – x4 + 2x5 = 1,
6x1 – x2 + x3 – 7x4 + x5 = 6,
3x1 + x2 – 3x3 + 4x4 – x5 = 3.
|
| 1.117.
x1 + 3x3 – x4 + x5 = 9,
2x1 + x2 – 5x3 + x4 – x5 = –10,
x1 – 3x2 + x3 – x4 – x5 = –1.
| 1.118.
7x1 – 2x2 – 4x3 + x5 = –10,
x1 – x2 + x3 + x4 – 6x5 = 8,
x1 + 2x2 + 2x3 – 3x4 = 11.
|
| 1.119.
3x1 – x2 + 4x3 – x4 – x5 = –8,
x1 + 10x2 – x3 – x4 + 2x5 = –9,
2x1 – x2 + 3x3 + x4 + x5 = 1.
| 1.120.
4x1 – 2x2 + x3 + x4 – x5 = 2,
x1 – 4x2 + 3x3 – x4 + x5 = 9,
2x1 + 2x2 – x3 – x4 + 3x5 = –8.
|



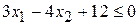 ; б)
; б)  .
.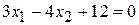 , найдя точки ее пересечения с осями координат
, найдя точки ее пересечения с осями координат 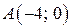 и
и  на рис. 1, а.
на рис. 1, а.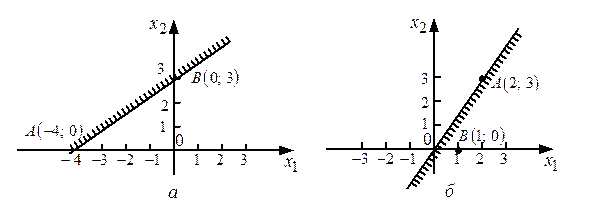
 , не лежащее на построенной прямой. Координаты точки
, не лежащее на построенной прямой. Координаты точки 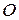 не удовлетворяют неравенству:
не удовлетворяют неравенству: 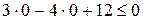 , следовательно, решением данного неравенства является нижняя полуплоскость, не содержащая контрольную точку
, следовательно, решением данного неравенства является нижняя полуплоскость, не содержащая контрольную точку  по двум точкам. Одной из этих точек является начало координат на рис. 1, б (в уравнении прямой отсутствует свободный член), а другую точку берем на прямой произвольно, например,
по двум точкам. Одной из этих точек является начало координат на рис. 1, б (в уравнении прямой отсутствует свободный член), а другую точку берем на прямой произвольно, например, 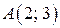 на рис. 1, б. В качестве контрольной возьмем, например, точку
на рис. 1, б. В качестве контрольной возьмем, например, точку 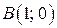 . Самую "простую" точку
. Самую "простую" точку 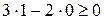 , то решением данного неравенства является нижняя (правая) полуплоскость, содержащая эту точку.
, то решением данного неравенства является нижняя (правая) полуплоскость, содержащая эту точку.


