Суперпозиция и замкнутые классы функций

Нульарные функции

При n = 0 количество булевых функций сводится к двум 2²⁰ = 2¹ = 2, первая из них тождественно равна 0, а вторая 1. Их называют булевыми константами — тождественный нуль и тождественная единица.
Таблица значений и названий нульарных булевых функций:

Значение	Обозначение	Название
0	F0,0 = 0	тождественный ноль
1	F0,1 = 1	тождественная единица

Унарные функции

При n = 1 число булевых функций равно 2²¹ = 2² = 4. Определение этих функций содержится в следующей таблице.

Таблица значений и названий булевых функций от одной переменной:

x 0 =x	1	0	Обозначение	Название
0	0	0	F1,0 = 0	тождественный ноль
1	0	1	F1,1 = x = x = x' = NOT(x)	отрицание, логическое «НЕТ», «НЕ», «НИ», инвертор, SWAP (обмен)
2	1	0	F1,2 = x	тождественная функция, логическое "ДА", повторитель
3	1	1	F1,3 = 1	тождественная единица, тавтология

Бинарные функции

При n = 2 число булевых функций равно 2²² = 2⁴ = 16.

Таблица значений и названий булевых функций от двух переменных:

x 0 =x	1	0	1	0
x 1 =y	1	1	0	0	Обозначение функции	Название функции
0	0	0	0	0	F2,0 = 0	тождественный ноль
1	0	0	0	1	F2,1 = x ↓ y = x NOR y = NOR(x, y) = x НЕ-ИЛИ y = НЕ-ИЛИ(x, y) = NOT(MAX(X,Y))	стрелка Пи́рса - "↓" (кинжал Куайна - "†"), функция Ве́бба - "°"[5], НЕ-ИЛИ, 2ИЛИ-НЕ, антидизъюнкция, инверсия максимума
2	0	0	1	0	F2,2 = x > y = x GT y = GT(x, y) = x → y = x ↛ y	функция сравнения "первый операнд больше второго операнда", инверсия прямой импликации
3	0	0	1	1	F2,3 = y = y' = y = NOT2(x, y) = НЕ2(x, y)	отрицание (негация, инверсия) второго операнда
4	0	1	0	0	F2,4 = x < y = x LT y = LT(x, y) = x ← y = x ↚ y	функция сравнения "первый операнд меньше второго операнда", инверсия обратной импликации
5	0	1	0	1	F2,5 = x = x' = x = NOT1(x, y) = НЕ1(x, y)	отрицание (негация, инверсия) первого операнда
6	0	1	1	0	F2,6 = x >< y = x <> y = x NE y = NE(x, y) = x ⊕ y = x XOR y = XOR(x, y)	функция сравнения "операнды не равны", сложение по модулю 2, исключающее «или», сумма Жегалкина[6]
7	0	1	1	1	F2,7 = x | y = x NAND y = NAND(x, y) = x НЕ-И y = НЕ-И(x, y) = NOT(MIN(X,Y))	штрих Ше́ффера, НЕ-И, 2И-НЕ, антиконъюнкция, инверсия минимума
8	1	0	0	0	F2,8 = x ∧ y = x · y = xy = x & y = x AND y = AND(x, y) = x И y = И(x, y) = min(x, y)	конъюнкция, 2И, минимум
9	1	0	0	1	F2,9 = (x ≡ y) = x ~ y = x ↔ y = x EQV y = EQV(x, y)	функция сравнения "операнды равны", эквивалентность
10	1	0	1	0	F2,10 = YES1(x, y) = ДА1(x, y) = x	первый операнд
11	1	0	1	1	F2,11 = x ≥ y = x >= y = x GE y = GE(x, y) = x ← y = x ⊂ y	функция сравнения "первый операнд не меньше второго операнда", обратная импликация (от второго аргумента к первому)
12	1	1	0	0	F2,12 = YES2(x, y) = ДА2(x, y) = y	второй операнд
13	1	1	0	1	F2,13 = x ≤ y = x <= y = x LE y = LE(x, y) = x → y = x ⊃ y	функция сравнения "первый операнд не больше второго операнда", прямая (материальная) импликация (от первого аргумента ко второму)
14	1	1	1	0	F2,14 = x ∨ y = x + y = x OR y = OR(x, y) = x ИЛИ y = ИЛИ(x, y) = max(x, y)	дизъюнкция, 2ИЛИ, максимум
15	1	1	1	1	F2,15 = 1	тождественная единица, тавтология

Суперпозиция и замкнутые классы функций

Результат вычисления булевой функции может быть использован в качестве одного из аргументов другой функции. Результат такой операции суперпозиции можно рассматривать как новую булеву функцию со своей таблицей истинности. Например, функции {\displaystyle f(x,y,z)={\overline {x({\overline {y}}\lor z)}}} (суперпозиция конъюнкции, дизъюнкции и двух отрицаний) будет соответствовать следующая таблица:

{\displaystyle x_{2}=x}	{\displaystyle x_{1}=y}	{\displaystyle x_{0}=z}		{\displaystyle f(x,y,z)}
0	0	0		1
0	0	1		1
0	1	0		1
0	1	1		1
1	0	0		0
1	0	1		0
1	1	0		1
1	1	1		0

Говорят, что множество функций замкнуто относительно операции суперпозиции, если любая суперпозиция функций из данного множества тоже входит в это же множество. Замкнутые множества функций называют также замкнутыми классами.

В качестве простейших примеров замкнутых классов булевых функций можно назвать множество {\displaystyle \{x\}}, состоящее из одной тождественной функции, или множество {\displaystyle \{0\}}, все функции из которого тождественно равны нулю вне зависимости от своих аргументов. Замкнуты также множество функций {\displaystyle \{x,{\overline {x}}\}} и множество всех унарных функций. А вот объединение замкнутых классов может таковым уже не являться. Например, объединив классы {\displaystyle \{0\}} и {\displaystyle \{x,{\overline {x}}\}}, мы с помощью суперпозиции {\displaystyle {\overline {0}}} сможем получить константу 1, которая в исходных классах отсутствовала.

Разумеется, множество {\displaystyle P_{2}} всех возможных булевых функций тоже является замкнутым.

Задача

У Бена Битдидла намечается пикник. Он не обрадуется,

если пойдёт дождь или появятся муравьи. Постройте

схему, в которой выход будет принимать значение

ИСТИНА только в том случае, если Бену пикник

понравится.

Решение: Сначала определим входы и выходы. Входами

будут переменные A и R, что означает муравьев (ants) и

дождь (rain). Значение А принимает значение ИСТИНА,

когда муравьи есть, и ЛОЖЬ, когда муравьев нет.

Аналогично, R имеет значение ИСТИНА, когда идёт

дождь, и ЛОЖЬ, когда Бену светит солнце. Выход E

(enjoyment, радость) показывает настроение Бена. E

имеет значение ИСТИНА, когда Бен радуется пикнику, и

ЛОЖЬ, когда он страдает.   показана таблица

истинности впечатлений Бена от пикника.

Используя дизъюнктивную форму, запишем уравнение

так: E = A¯ R¯ или E = Σ(0). Мы можем реализовать

соответствующую схему, используя два инвертора и

двухвходовой элемент И, как показано на Рис. 2.11 (а).

Вы могли заметить, что эта таблица является точно такой

же, как и таблица для функции «ИЛИ-НЕ»,

рассмотренной в: E = A ИЛИ-НЕ R = A + R

На Рис.   показана реализация на базе элемента ИЛИ-НЕ.

мы покажем, что выражения AR и A + R эквивалентны.  

                                                                                       Е

Е

Схема Бена

Таблица истинности Бена

A R E

0 0 1

0 1 0

1 0 0

1 1 1

Совершенная дизъюнктивная нормальная форма позволяет записать

булево уравнение для любой таблицы истинности с любым

количеством переменных. На Рис. 2.12 показана произвольная таблица

истинности для трехвходового элемента. Совершенная дизъюнктивная

нормальная форма соответствующей логической функции выглядит так:

Y = A¯ B¯ C¯ + A B¯ C¯ + A B¯ C

или (2.3)

Y = Σ(0, 4, 5)

Отрицание, НЕ

Инвертор, НЕ (IEC)

Инвертор, НЕ (ANSI)

{\displaystyle A} АА	А{\displaystyle A}
0	1
1	0

Мнемоническое правило для отрицания звучит так: На выходе будет:

· «1» тогда и только тогда, когда на входе «0»,

· «0» тогда и только тогда, когда на входе «1»

Повторение

Повторитель (буфер)

{\displaystyle A} А	{\displaystyle A} А
0	0
1	1

Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.

Из {\displaystyle 2^{(2^{2})}=2^{4}=16} возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.

Конъюнкция (логическое умножение). Операция И ]

И (IEC)

И (ANSI)

{\displaystyle A} А	А{\displaystyle B}	{\displaystyle A\land B} А^В
0	0	0
0	1	0
1	0	0
1	1	1

Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:

· «1» тогда и только тогда, когда на всех входах действуют «1»,

· «0» тогда и только тогда, когда хотя бы на одном входе действует «0»

Словесно эту операцию можно выразить следующим выражением: «Истина на выходе может быть при истине на входе 1 И истине на входе 2».

К155ЛА8 КМ155ЛА8 (7401)

 

Микросхемы К155ЛА8, КМ155ЛА8 (7401) представляют собой четыре логических элемента 2И-НЕ. Корпус К155ЛА8 (7401) типа 201.14-1, масса около 1 грамма и у КМ155ЛА8 (7401) типа 201.14-8, масса около 2,2 грамма.

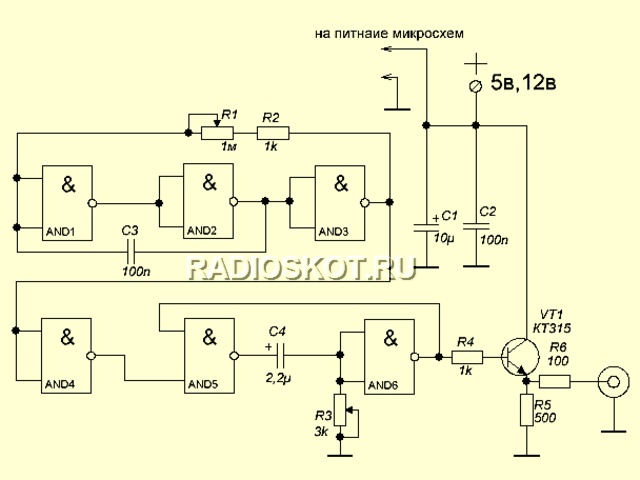
ГЕНЕРАТОР ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ
Питание: 5-12в --- Частота: 5Гц-1кГц. --- Амплитуда выходных импульсов не менее 10в --- Ток: около 100мА.

 

 

 

 

 

Нульарные функции

При n = 0 количество булевых функций сводится к двум 2²⁰ = 2¹ = 2, первая из них тождественно равна 0, а вторая 1. Их называют булевыми константами — тождественный нуль и тождественная единица.
Таблица значений и названий нульарных булевых функций:

Значение	Обозначение	Название
0	F0,0 = 0	тождественный ноль
1	F0,1 = 1	тождественная единица

Унарные функции

При n = 1 число булевых функций равно 2²¹ = 2² = 4. Определение этих функций содержится в следующей таблице.

Таблица значений и названий булевых функций от одной переменной:

x 0 =x	1	0	Обозначение	Название
0	0	0	F1,0 = 0	тождественный ноль
1	0	1	F1,1 = x = x = x' = NOT(x)	отрицание, логическое «НЕТ», «НЕ», «НИ», инвертор, SWAP (обмен)
2	1	0	F1,2 = x	тождественная функция, логическое "ДА", повторитель
3	1	1	F1,3 = 1	тождественная единица, тавтология

Бинарные функции

При n = 2 число булевых функций равно 2²² = 2⁴ = 16.

Таблица значений и названий булевых функций от двух переменных:

x 0 =x	1	0	1	0
x 1 =y	1	1	0	0	Обозначение функции	Название функции
0	0	0	0	0	F2,0 = 0	тождественный ноль
1	0	0	0	1	F2,1 = x ↓ y = x NOR y = NOR(x, y) = x НЕ-ИЛИ y = НЕ-ИЛИ(x, y) = NOT(MAX(X,Y))	стрелка Пи́рса - "↓" (кинжал Куайна - "†"), функция Ве́бба - "°"[5], НЕ-ИЛИ, 2ИЛИ-НЕ, антидизъюнкция, инверсия максимума
2	0	0	1	0	F2,2 = x > y = x GT y = GT(x, y) = x → y = x ↛ y	функция сравнения "первый операнд больше второго операнда", инверсия прямой импликации
3	0	0	1	1	F2,3 = y = y' = y = NOT2(x, y) = НЕ2(x, y)	отрицание (негация, инверсия) второго операнда
4	0	1	0	0	F2,4 = x < y = x LT y = LT(x, y) = x ← y = x ↚ y	функция сравнения "первый операнд меньше второго операнда", инверсия обратной импликации
5	0	1	0	1	F2,5 = x = x' = x = NOT1(x, y) = НЕ1(x, y)	отрицание (негация, инверсия) первого операнда
6	0	1	1	0	F2,6 = x >< y = x <> y = x NE y = NE(x, y) = x ⊕ y = x XOR y = XOR(x, y)	функция сравнения "операнды не равны", сложение по модулю 2, исключающее «или», сумма Жегалкина[6]
7	0	1	1	1	F2,7 = x | y = x NAND y = NAND(x, y) = x НЕ-И y = НЕ-И(x, y) = NOT(MIN(X,Y))	штрих Ше́ффера, НЕ-И, 2И-НЕ, антиконъюнкция, инверсия минимума
8	1	0	0	0	F2,8 = x ∧ y = x · y = xy = x & y = x AND y = AND(x, y) = x И y = И(x, y) = min(x, y)	конъюнкция, 2И, минимум
9	1	0	0	1	F2,9 = (x ≡ y) = x ~ y = x ↔ y = x EQV y = EQV(x, y)	функция сравнения "операнды равны", эквивалентность
10	1	0	1	0	F2,10 = YES1(x, y) = ДА1(x, y) = x	первый операнд
11	1	0	1	1	F2,11 = x ≥ y = x >= y = x GE y = GE(x, y) = x ← y = x ⊂ y	функция сравнения "первый операнд не меньше второго операнда", обратная импликация (от второго аргумента к первому)
12	1	1	0	0	F2,12 = YES2(x, y) = ДА2(x, y) = y	второй операнд
13	1	1	0	1	F2,13 = x ≤ y = x <= y = x LE y = LE(x, y) = x → y = x ⊃ y	функция сравнения "первый операнд не больше второго операнда", прямая (материальная) импликация (от первого аргумента ко второму)
14	1	1	1	0	F2,14 = x ∨ y = x + y = x OR y = OR(x, y) = x ИЛИ y = ИЛИ(x, y) = max(x, y)	дизъюнкция, 2ИЛИ, максимум
15	1	1	1	1	F2,15 = 1	тождественная единица, тавтология

Суперпозиция и замкнутые классы функций

Результат вычисления булевой функции может быть использован в качестве одного из аргументов другой функции. Результат такой операции суперпозиции можно рассматривать как новую булеву функцию со своей таблицей истинности. Например, функции {\displaystyle f(x,y,z)={\overline {x({\overline {y}}\lor z)}}} (суперпозиция конъюнкции, дизъюнкции и двух отрицаний) будет соответствовать следующая таблица:

{\displaystyle x_{2}=x}	{\displaystyle x_{1}=y}	{\displaystyle x_{0}=z}		{\displaystyle f(x,y,z)}
0	0	0		1
0	0	1		1
0	1	0		1
0	1	1		1
1	0	0		0
1	0	1		0
1	1	0		1
1	1	1		0

Говорят, что множество функций замкнуто относительно операции суперпозиции, если любая суперпозиция функций из данного множества тоже входит в это же множество. Замкнутые множества функций называют также замкнутыми классами.

В качестве простейших примеров замкнутых классов булевых функций можно назвать множество {\displaystyle \{x\}}, состоящее из одной тождественной функции, или множество {\displaystyle \{0\}}, все функции из которого тождественно равны нулю вне зависимости от своих аргументов. Замкнуты также множество функций {\displaystyle \{x,{\overline {x}}\}} и множество всех унарных функций. А вот объединение замкнутых классов может таковым уже не являться. Например, объединив классы {\displaystyle \{0\}} и {\displaystyle \{x,{\overline {x}}\}}, мы с помощью суперпозиции {\displaystyle {\overline {0}}} сможем получить константу 1, которая в исходных классах отсутствовала.

Разумеется, множество {\displaystyle P_{2}} всех возможных булевых функций тоже является замкнутым.

Задача

У Бена Битдидла намечается пикник. Он не обрадуется,

если пойдёт дождь или появятся муравьи. Постройте

схему, в которой выход будет принимать значение

ИСТИНА только в том случае, если Бену пикник

понравится.

Решение: Сначала определим входы и выходы. Входами

будут переменные A и R, что означает муравьев (ants) и

дождь (rain). Значение А принимает значение ИСТИНА,

когда муравьи есть, и ЛОЖЬ, когда муравьев нет.

Аналогично, R имеет значение ИСТИНА, когда идёт

дождь, и ЛОЖЬ, когда Бену светит солнце. Выход E

(enjoyment, радость) показывает настроение Бена. E

имеет значение ИСТИНА, когда Бен радуется пикнику, и

ЛОЖЬ, когда он страдает.   показана таблица

истинности впечатлений Бена от пикника.

Используя дизъюнктивную форму, запишем уравнение

так: E = A¯ R¯ или E = Σ(0). Мы можем реализовать

соответствующую схему, используя два инвертора и

двухвходовой элемент И, как показано на Рис. 2.11 (а).

Вы могли заметить, что эта таблица является точно такой

же, как и таблица для функции «ИЛИ-НЕ»,

рассмотренной в: E = A ИЛИ-НЕ R = A + R

На Рис.   показана реализация на базе элемента ИЛИ-НЕ.

мы покажем, что выражения AR и A + R эквивалентны.  

                                                                                       Е

Е

Схема Бена

Таблица истинности Бена

A R E

0 0 1

0 1 0

1 0 0

1 1 1

Совершенная дизъюнктивная нормальная форма позволяет записать

булево уравнение для любой таблицы истинности с любым

количеством переменных. На Рис. 2.12 показана произвольная таблица

истинности для трехвходового элемента. Совершенная дизъюнктивная

нормальная форма соответствующей логической функции выглядит так:

Y = A¯ B¯ C¯ + A B¯ C¯ + A B¯ C

или (2.3)

Y = Σ(0, 4, 5)

Отрицание, НЕ

Инвертор, НЕ (IEC)

Инвертор, НЕ (ANSI)

{\displaystyle A} АА	А{\displaystyle A}
0	1
1	0

Мнемоническое правило для отрицания звучит так: На выходе будет:

· «1» тогда и только тогда, когда на входе «0»,

· «0» тогда и только тогда, когда на входе «1»

Повторение

Повторитель (буфер)

{\displaystyle A} А	{\displaystyle A} А
0	0
1	1

Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.

Из {\displaystyle 2^{(2^{2})}=2^{4}=16} возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.

Конъюнкция (логическое умножение). Операция И ]

И (IEC)

И (ANSI)

{\displaystyle A} А	А{\displaystyle B}	{\displaystyle A\land B} А^В
0	0	0
0	1	0
1	0	0
1	1	1

Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:

· «1» тогда и только тогда, когда на всех входах действуют «1»,

· «0» тогда и только тогда, когда хотя бы на одном входе действует «0»

Словесно эту операцию можно выразить следующим выражением: «Истина на выходе может быть при истине на входе 1 И истине на входе 2».