Также большую роль в научно-исследовательской работе школьников играют научно-исследовательские конференции и семинары. Их основная цель - установление научного сотрудничества, поиск путей для взаимовыгодной исследовательской деятельности между учеными и преподавателями различных кафедр, с одной стороны, и старшеклассниками, с другой.
Практическая задача семинаров и конференций, направлена на осуществление основной цели, - изучение дополнительных тем математики, проведение исследовательской работы в специальных группах (секциях, минисеминарах) по конкретным научным проблемам или задачам исследовательского характера, с вынесением важнейших достижений, результатов, а также возникающих новых проблем на общий постоянно действующий семинар, а затем на конференции различного уровня (от школьных до международных).
Методы и приемы научно-исследовательской работы школьников
Неполная индукция
Неполная индукция - тип индуктивных умозаключений, посылки которых являются единичными суждениями, содержащими эмпирические данные об исследованных объектах некоторой области, а заключение - общим суждением обо всех предметах данной области или о некоторых, неисследованных предметах этой же. Доказательная сила Неполной индукции ограничена, поскольку связь между её посылками и заключением носит вероятностный, проблематичный характер. И тем не менее, именно Неполная индукция есть основной путь получения новых знаний, в отличие от так называемой полной индукции, посылки и заключение которой содержат в точности одну и ту же информацию.
Неполная индукция - индуктивный вывод о том, что всем представителям изучаемого множества принадлежит свойство Р на том основании, что Р принадлежит некоторым представителям этого множества. Так, напр., узнав о том, что инженер А работает продавцом, инженер B работает продавцом и инженер С также работает продавцом, вы можете сделать индуктивный вывод, что все инженеры ныне работают продавцами. Множество инженеров велико, трудно или даже невозможно установить, чем сейчас занимается каждый из них, поэтому ваше индуктивное заключение связано с риском: оно может оказаться ошибочным.
Неполная индукция дает вероятностное заключение и применяется при невозможности рассмотрения всех без исключения случаев. К неполной индукции относится перечислительная, аналитическая, научная.
Перечислительная (популярная) индукция осуществляется на основании повторяемости одного и того же признака у ряда факторов и отсутствия противоречивого случая, выводом что, все факторы этого рода имеют указанный признак. Так, обнаруживая массу у всех известных ему предметов, Ньютон обобщил: "Все тела имеют массу". Но подобные обобщения не всегда правомерны. Примером поспешного обобщения служат лебеди: европейцы считали что, все лебеди белые, пока не обнаружили в Австралии черных. Поскольку перечислительная индукция допускает исключения из правил, ее выводы лишь правдоподобны, а не достоверны. Уверенность в их истинности растет с появлением новых подтверждений, но утверждение ее возможно лишь через другие способы умозаключений.
Аналитическая индукция с целью исключить случаи поспешного обобщения предполагает выбор наиболее типичных факторов, разнородных по времени и другим возможным условиям. Например, о качестве партии товара судят по образцам из разных вагонов и разных мест вагона (при перечислительной индукции, проверяющие полностью проверили бы 2 вагона из 50 и, уморившись, решили бы: "Да че там проверять - вся партия такая!" - а в следующем вагоне могла бы начаться другая картина).
Научная индукция обобщает путем отбора необходимых и исключения случайных обстоятельств, учитывая важнейшую из необходимых связей - причинную и, при условии что, выбранная связь сочтена причинной не ошибочно, дает абсолютно достоверную информацию обо всех явлениях, какого либо класса на основании изучения некоторого их числа. При этом возможность установления причинной связи обусловлена тем что, если достоверно известно что, во всяких ситуациях, при всяких стечениях обстоятельств, только одно, в своем отличии, необходимо для отличия в исследуемом явлении, то оно и есть его причина.
Обобщение
Обобщение есть переход от рассмотрения данного множества предметов к рассмотрению большего множества, содержащего данное. Например, мы делаем обобщение, когда переходим от рассмотрения треугольников к рассмотрению многоугольников с произвольным числом сторон. Мы делаем обобщение и когда переходим от изучения тригонометрических функций острого угла к изучению тригонометрических функции произвольного угла.
Обобщение - как метод научного познания, во-первых, логический процесс перехода от единичного к общему, от менее общего к более общему знанию, установления общих свойств и признаков предметов, во-вторых, - результат этого процесса: обобщенное понятие, суждение, закон, теория. Получение обобщенного знания означает более глубокое отражение действительности, проникновение в ее сущность. Принято различать два вида научных обобщений: выделение любых признаков (абстрактно-общее) или существенных (конкретно-общее, т.е. закон).
По другому основанию можно выделить обобщения:
а) от отдельных фактов, событий к их выражению в мыслях (индуктивное обобщение);
б) от одной мысли к другой, более общей мысли (логическое обобщение). Мысленный переход от более общего к менее общему есть процесс ограничения.
Обобщение не может быть беспредельным. Его пределом являются философские категории, которые не имеют родового понятия и потому обобщить их нельзя.
Аналогия
Аналогия есть некоторого рода сходство. Она, можно сказать, есть сходство, но на более определенном и выражаемом с помощью понятий уровне. Однако мы можем выразиться несколько более точно. Существенное различие между аналогией и другими видами сходства заключается, как мне кажется, в намерениях думающего. Сходные предметы согласуются между собой в каком-то отношении. Если вы намереваетесь свести это отношение, в котором они согласуются, к определенным понятиям, то вы рассматриваете эти сходные предметы как аналогичные. Если вам удается добраться до ясных понятий, то вы выяснили аналогию.
Сравнивая молодую женщину с цветком, поэты ощущают, я надеюсь, некоторое сходство, но обычно они не имеют в виду аналогии. Действительно, они едва ли намериваются покинуть мир эмоций и свести это сравнение к чему-то измеримому или определимому с помощью понятий.
Рассматривая в музее естественной истории скелеты различных млекопитающих, вы можете обнаружить, что все они страшны. Если в этом все сходство, которое вы между ними обнаружили, то вы видите не такую уж сильную аналогию. Однако вы можете подметить удивительно много говорящую аналогию, если рассмотрите руку человека, лапу кошки, переднюю ногу лошади, плавник кита и крыло летучей мыши - эти столь различно используемые органы, как состоящие из сходных частей, имеющих сходное отношение друг к другу.
Аналогия есть умозаключение о принадлежности единичному явлению определенного признака на основе сходства этого явления в существенных признаках с другим уже известным единичным явлением. Она рассматривается в качестве разновидности индукции.
Приведем следующий пример умозаключения по аналогии: Для существования живых существ необходимы вода, воздух, соответствующая температура и т.д. На Марсе есть вода, воздух, соответствующая температура и т.д. Следовательно, на Марсе, возможно, существуют живые существа. Поскольку в данном силлогизме содержится ошибка, заключающаяся в том, что среднее понятие не распределено (ложность нераспределенного среднего термина), ценность заключения находится на уровне вероятности. Однако если среднее понятие будет распределенным (то есть, если будут установлены все условия, необходимые для существования живых существ), то и заключение станет определенным.
Другими словами, аналогия - это подобие, сходство предметов или явлений в каких-либо свойствах, признаках, отношениях, причем сами эти предметы, вообще говоря, различны. В математике часто рассматривают умозаключение по аналогии, сходству отдельных свойств (признаков) при сравнении двух множеств (фигур, отношений, объектов и т.д.).
Аналогия весьма доступна и проста как прием рассуждения, но она в первую очередь позволяет выдвинуть гипотезу, которую потом требуется строго доказать.
Специализация
Специализация есть переход от рассмотрения данного множества предметов к рассмотрению меньшего множества, содержащегося в данном.
Например, мы специализируем, когда переходим от рассмотрения многоугольников к рассмотрению правильных многоугольников, п специализируем еще дальше, когда переходим от правильных многоугольников с п сторонами к правильному, т.е. равностороннему треугольнику.
Эти два последовательных перехода осуществлялись в двух характерно различных направлениях. В первом переходе, от многоугольников к правильным многоугольникам, мы ввели ограничение, именно потребовали, чтобы все стороны и все углы многоугольника были равны. Во втором переходе мы заменили переменный предмет конкретным, поставили 3 вместо переменного целого числа п.
Очень часто мы производим специализацию, переходя от целого класса предметов к одному предмету, содержащемуся в этом классе. Например, когда мы хотим проверить некоторое общее утверждение относительно простых чисел, мы выбираем какое-нибудь простое число, скажем 17, и исследуем, справедливо ли это общее утверждение или нет именно для этого числа 17.
Пример задачи исследовательского характера для школьников
Пример 1: неприводимые многочлены
Многочлен h (x) с целыми коэффициентами положительной степени называется неприводимым, если он не представим в виде произведения двух многочленов положительных степеней с целыми коэффициентами.
Пусть g (x) = (x - a 1) … (x - an), где a 1,…, an - различные целые числа.
Пусть f (x) = mx +1, где m - целое число. Найдите все значения m, для которых многочлен f (g (x)) неприводим.
Пусть f (x) = mx 2+1, где m - натуральное число. Докажите, что многочлен f (g (x)) неприводим.
Исследуйте неприводимость многочленов вида f (g (x)) для других неприводимых многочленов f (x) (например, для неприводимых квадратичных многочленов ax 2+ bx +1).
Решение.
1. Предположим, что многочлен f (g (x)) приводим, то есть для некоторых двух многочленов f 1 (x) и f 2 (x) положительной степени с целыми коэффициентами
m (x - a 1) … (x - an) +1 = f 1 (x) f 2 (x).
Это верно для всех x, в том числе и для x = a 1, …, x = an. Получаем,
f 1 (a 1) f 2 (a 1) =1,…,
f 1 (an) f 2 (an) =1.
Рассмотрим первое из этих равенств. Оно возможно для целого a 1 и многочленов f 1 (x), f 2 (x) с целыми коэффициентами только если f 1 (a 1) = f 2 (a 1) =1 или f 1 (a 1) = f 2 (a 1) =-1. Аналогично и для остальных равенств. Пусть в i случаях будет 1, в j будет - 1. Тогда i + j = n.
Покажем, что n - четное и i = j =  . Допустим, что i >
. Допустим, что i > 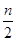 (т.е. j = n - i <
(т.е. j = n - i < 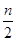 ). Тогда многочлены f 1 (x) - 1 и f 2 (x) - 1 имеют не менее i корней, а, следовательно, их степень больше
). Тогда многочлены f 1 (x) - 1 и f 2 (x) - 1 имеют не менее i корней, а, следовательно, их степень больше  . Поэтому и степени многочленов f 1 (x) и f 2 (x) соответственно больше
. Поэтому и степени многочленов f 1 (x) и f 2 (x) соответственно больше 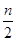 . Таким образом степень f 1 (x) f 2 (x) = m (x - a 1) … (x - an) +1 больше n. Противоречие показывает, что допущенное не верно. Аналогично, j не больше
. Таким образом степень f 1 (x) f 2 (x) = m (x - a 1) … (x - an) +1 больше n. Противоречие показывает, что допущенное не верно. Аналогично, j не больше 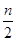 .
.
Два числа не превосходящие  в сумме дают n. Значит, i = j =
в сумме дают n. Значит, i = j = 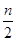 и n - четное число. При этом степени f 1 (x) и f 2 (x) также равны i =
и n - четное число. При этом степени f 1 (x) и f 2 (x) также равны i =  , иначе, рассуждая как и выше, получим противоречие.
, иначе, рассуждая как и выше, получим противоречие.
Не ограничивая общности, можно считать, что f 1 (a 1) =…= f 1 (ai) =1, f 1 (ai +1) =…= f 1 (an) =-1. (При перестановке местами a k и a l условие задачи не изменится, поэтому можно считать, что изначально их порядок такой, что f 1 (x) обращается в 1 в первых i). Тогда f 1 (x) = t 1× (x - a 1) … … (x - ai) +1 = t 2× (x - ai +1) … (x - an) -1. Аналогично, f 2 (x) = d 1× (x - a 1) … (x - ai) +1 = d 2× (x - ai +1) … (x - an) -1.
Рассмотрим равенства
m (x - a 1) … (x - an) +1 = f 1 (x) f 2 (x) = (t 1× (x - a 1) … (x - ai) +1) × (d 1× (x - a 1) … (x - ai) +1);
m (x - a 1) … (x - an) +1 = f 1 (x) f 2 (x) = (t 1× (x - a 1) … (x - ai) +1) × (d 2× (x - ai +1) … (x - an) -1).
Приравнивая коэффициенты при старшей степени (xn) левой и правой части, получаем m = t 1 d 1 и m = t 1 d 2. Отсюда d 1 = d 2. Аналогично получаем, что t 1 = t 2. Таким образом, получаем, что m = t × d для некоторых целых t и d, причем:
f 1 (x) = t × (x - a 1) … (x - ai) +1 = t × (x - ai +1) … (x - an) -1
f 2 (x) = d × (x - a 1) … (x - ai) +1 = d × (x - ai +1) … (x - an) -1.
Вычтем из первого равенства второе
t × (x - a 1) … (x - ai) - d × (x - a 1) … (x - ai) = t × (x - ai +1) … (x - an) - d × (x - ai +1) … (x - an),
откуда, преобразовывая, получим
t × ((x - a 1) … (x - ai) - (x - ai +1) … (x - an)) = d × ((x - a 1) … (x - ai) - (x - ai +1) … (x - an)).
Это равенство выполнено для всех x, поэтому можно считать, что
(x - a 1) … (x - ai) - (x - ai +1) … (x - an) ¹ 0, и t = d.
Таким образом,
f 1 (x) = f 2 (x) = t × (x - a 1) … (x - ai) +1 = t × (x - ai +1) … (x - an) -1.
Применим к этому равенству обобщенную теорему Виета и рассмотрим свободные члены
(-1) i × t × a 1×…× ai +1 = (-1) i × t × ai +1×…× an -1.
Перенесем слагаемые с t влево, без t вправо. Вынесем t за скобки
t × (a 1×…× ai - ai +1×…× an) = ±2.
Выражение в скобках - целое число. Поэтому t может принимать только 4 различные значения: ±1 и ±2. Но как показано выше, m = t × t. Следовательно только для двух целых значений m многочлен f (g (x)) приводим. Это m = 1 и m = 4.
Приведем примеры приводимых многочленов для этих m.
(x -1) (x -2) (x -3) (x -4) + 1 = ((x -1) (x -4) +1) × ((x -2) (x -3) -1)
Действительно, ((x -1) (x -4) +1) × ((x -2) (x -3) -1) = (x -1) (x -2) (x -3) (x -4) - x 2+5 x - 4 + x 2 - 5 x +6-1= = (x -1) (x -2) (x -3) (x -4) + 1.
Для m = 4
4 x (x -1) +1 = 4 x 2 - 4 x + 1 = (2 x -1) (2 x -1)
Ответ: f (g (x)) неприводим при всех целых m Ï{1; 4}.
2. Допустим, что m (x - a 1) 2… (x - an) 2+1 приводим, тогда
m (x - a 1) 2… (x - an) 2+1 = f 1 (x) f 2 (x).
Как и выше, f 1 (x) = f 2 (x) =1 либо f 1 (x) = f 2 (x) = - 1 для всех x из { a 1; …; an }. Если f 1 (x) принимает значения и 1 и - 1, то в силу непрерывности многочлена, f 1 (x) = 0 для некоторого x. Но тогда для этого x выполнено равенство
m (x - a 1) 2… (x - an) 2+1 = f 1 (x) f 2 (x) = 0,
чего быть не может ни при одном натуральном m. Поэтому для определенности будем считать, что f 1 (ai) = f 2 (ai) =1 для всех i от 1 до n. (В случае, когда, f 1 (ai) = f 2 (ai) =-1 для всех i от 1 до n доказательство проводится аналогично) Как и в пункте 1, получаем
f 1 (x) = t × (x - a 1) … (x - an) +1;
f 2 (x) = d × (x - a 1) … (x - an) +1.
Отсюда,
m (x - a 1) 2… (x - an) 2+1 = f 1 (x) × f 2 (x) = t × d × (x - a 1) 2… (x - an) 2+ (t + d) × (x - a 1) … (x - an) +1.
Из равенства многочленов получаем m = t × d и (t + d) × (x - a 1) … (x - an) = 0. Последнее равенство выполнено при всех значениях x, поэтому из него следует, что t + d = 0, то есть t = - d. Откуда натуральное m = - t 2. Противоречие показывает, что многочлен m (x - a 1) 2… (x - an) 2+1 неприводим. Утверждение доказано.
3. Рассмотрим неприводимый многочлен ax 2+ bx +1. Допустим, дискриминант b 2-4 a <0, а многочлен a × (x - a 1) 2… (x - an) 2 + b × (x - a 1) … (x - an) +1 = f 1 (x) × f 2 (x) приводим. Как и в пункте 2, учитывая, что при отрицательном дискриминанте многочлен не будет обращаться в 0, получаем:
f 1 (x) = t × (x - a 1) … (x - an) +1;
f 2 (x) = d × (x - a 1) … (x - an) +1.
Отсюда,
a × (x - a 1) 2… (x - an) 2 + b × (x - a 1) … (x - an) +1 =
= f 1 (x) × f 2 (x) = t × d × (x - a 1) 2… (x - an) 2+ (t + d) × (x - a 1) … (x - an) +1.
Из равенства многочленов получаем, что a = t × d и b = t + d. Значит t и d являются корнями уравнения x 2 - bx + a = 0. Но согласно предположению дискриминант этого уравнения b 2-4 a <0. Уравнение не имеет корней. Таким образом допущение не верно и при отрицательном дискриминанте многочлен a × (g (x)) 2+ b × g (x) +1 неприводим.
Пример 2: волнистые числа
Назовем девятизначное число  волнистым числом первого типа, если
волнистым числом первого типа, если


Например, число 162539581 волнистое число первого типа. Назовем девятизначное число волнистым числом второго типа, если


а) Найдите количество девятизначных волнистых чисел первого и второго типа.
б) Найдите формулу для вычисления количества волнистых п -значных чисел первого и второго типа.
Назовем девятизначное число  волнистым числом третьего типа, если
волнистым числом третьего типа, если


Назовем девятизначное число волнистым числом четвертого типа, если


а) Найдите количество девятизначных волнистых чисел третьего и четвертого типа.
б) Найдите формулу для вычисления количества волнистых п -значных чисел третьего и четвертого типа.
Предложите свои обобщения этой задачи и исследуйте их.
Решение
Лемма 1. Обозначим через f (n, k 1, k 2) - количество n -значных волнистых чисел первого типа, начинающихся с цифры k 1 и заканчивающиеся на цифру k 2, g (n, k 1, k 2) - количество n -значных волнистых чисел второго типа, начинающихся с цифры k 1 и заканчивающиеся на цифру k 2. Тогда
 и
и
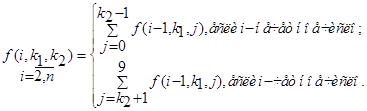
Также,  и
и

Доказательство. Рассмотрим n -значные волнистые числа первого типа.
Нетрудно заметить, как они получаются. Берутся все n -1-значные волнистые числа и, в зависимости от текущего знака (“<" или ”>”), дописывается каждому числу цифра, меньшая или большая последней, т.е. чтобы найти количество n -значных волнистых чисел, заканчивающихся на k, надо найти сумму всех количеств n -1-значных чисел заканчивающихся на цифры от 0 до k- 1 или от k +1 до 9.Т. к. на каждом шаге мы корректно вычисляем волнистые числа, то нет необходимости знать всё число: все зависит от последней цифры.
Следовательно, можно составить рекуррентную формулу, которая будет корректно вычислять количество n -значных волнистых чисел первого типа начинающихся на цифру k 1 и заканчивающихся на цифру k 2.
Рассмотрим рекуррентную формулу для волнистых чисел первого типа.
Начальные её значения 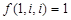 , т.е. есть только по одному однозначному волнистому числу, начинающемуся на i и заканчивающемуся на i (
, т.е. есть только по одному однозначному волнистому числу, начинающемуся на i и заканчивающемуся на i ( ).
).
Пусть  , тогда по четности/нечетности i (
, тогда по четности/нечетности i ( ) определяем текущий знак “<” или “>”:
) определяем текущий знак “<” или “>”:
Если i -нечетное, то 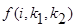 является суммой всех количеств i -1-значные волнистых чисел первого типа, которые начинаются на k 1 и у которых последняя цифра меньше k 2.
является суммой всех количеств i -1-значные волнистых чисел первого типа, которые начинаются на k 1 и у которых последняя цифра меньше k 2.
Если i -четное, то  является суммой всех количеств i -1-значные волнистых чисел первого типа, которые начинаются на k 1 и у которых последняя цифра больше k 2.
является суммой всех количеств i -1-значные волнистых чисел первого типа, которые начинаются на k 1 и у которых последняя цифра больше k 2.
Аналогично, выводится рекуррентное соотношение для волнистых чисел второго типа.
Теорема 1. Количество n -значных волнистых чисел первого типа:

и количество n -значных волнистых чисел второго типа:
 .
.
Составим таблицу некоторых значений f (n, k, k 2)
| k
| 
| 
| 
| 
| 
|
| 0
| 1
| 0
| 0
| 0
| 0
|
| 1
| 1
| 8
| 44
| 276
| 1650
|
| 2
| 1
| 7
| 42
| 259
| 1561
|
| 3
| 1
| 6
| 39
| 235
| 1430
|
| 4
| 1
| 5
| 35
| 205
| 1260
|
| 5
| 1
| 4
| 30
| 170
| 1055
|
| 6
| 1
| 3
| 24
| 131
| 820
|
| 7
| 1
| 2
| 17
| 89
| 561
|
| 8
| 1
| 1
| 9
| 45
| 285
|
| 9
| 1
| 0
| 0
| 0
| 0
|
| 
| 10
| 36
| 240
| 1410
| 8622
|
| | | | | | | |
| k
| 
| 
| 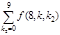
| 
|
| 0
| 0
| 0
| 0
| 0
|
| 1
| 10032
| 60654
| 367422
| 2224299
|
| 2
| 9471
| 57309
| 347073
| 2101296
|
| 3
| 8651
| 52403
| 317253
| 1920984
|
| 4
| 7596
| 46067
| 278782
| 1688269
|
| 5
| 6336
| 38471
| 232715
| 1409487
|
| 6
| 4906
| 29820
| 180312
| 1092234
|
| 7
| 3345
| 20349
| 123003
| 745161
|
| 8
| 1695
| 10317
| 62349
| 377739
|
| 9
| 0
| 0
| 0
| 0
|

| 52032
| 315390
| 1908909
| 11559469
|
Составим таблицу некоторых значений g (n, k, k 2)
| k
| 
| 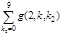
| 
| 
| 
|
| 0
| 1
| 0
| 0
| 0
| 0
|
| 1
| 1
| 1
| 9
| 45
| 285
|
| 2
| 1
| 2
| 17
| 89
| 561
|
| 3
| 1
| 3
| 24
| 131
| 820
|
| 4
| 1
| 4
| 30
| 170
| 1055
|
| 5
| 1
| 5
| 35
| 205
| 1260
|
| 6
| 1
| 6
| 39
| 235
| 1430
|
| 7
| 1
| 7
| 42
| 259
| 1561
|
| 8
| 1
| 8
| 44
| 276
| 1650
|
| 9
| 1
| 9
| 45
| 285
| 1695
|
| 
| 10
| 45
| 285
| 1695
| 10317
|
| k
| 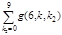
| 
| 
| 
|
| 0
| 0
| 0
| 0
| 0
|
| 1
| 1695
| 10317
| 62349
| 377739
|
| 2
| 3345
| 20349
| 123003
| 745161
|
| 3
| 4906
| 29820
| 180312
| 1092234
|
| 4
| 6336
| 38471
| 232715
| 1409487
|
| 5
| 7596
| 46067
| 278782
| 1688269
|
| 6
| 8651
| 52403
| 317253
| 1920984
|
| 7
| 9471
| 57309
| 347073
| 2101296
|
| 8
| 10032
| 60654
| 367422
| 2224299
|
| 9
| 10317
| 62349
| 377739
| 2286648
|

| 62349
| 377739
| 2286648
| 13846117
|
Ответ:
а) первого типа: 11559469; второго типа: 13846117
б) 

Лемма 2. Обозначим через t (n, k 1, k 2) - количество n -значных волнистых чисел третьего типа, начинающихся с цифры k 1 и заканчивающиеся на цифру k 2, r (n, k 1, k 2) - количество n -значных волнистых чисел четвертого типа, начинающихся с цифры k 1 и заканчивающиеся на цифру k 2. Тогда
 и
и

Также  и
и 
Доказательство. Рассмотрим n -значные волнистые числа третьего типа.
Нетрудно заметить, как они получаются. Берутся все n -1-значные волнистые числа и, в зависимости от текущего знака (”  ", ”<”, ”>", ”
", ”<”, ”>", ”  ”), дописывается каждому числу цифра, меньшая, равная или большая последней, т.е. чтобы найти количество n -значных волнистых чисел, заканчивающихся на k, надо найти сумму всех количеств n -1-значных чисел заканчивающихся на цифры от 0 до k, или от 0 до k +1, или от k +1 до 9, или от k до 9.Т. к. на каждом шаге мы корректно вычисляем волнистые числа, то нет необходимости знать всё число: все зависит от последней цифры.
”), дописывается каждому числу цифра, меньшая, равная или большая последней, т.е. чтобы найти количество n -значных волнистых чисел, заканчивающихся на k, надо найти сумму всех количеств n -1-значных чисел заканчивающихся на цифры от 0 до k, или от 0 до k +1, или от k +1 до 9, или от k до 9.Т. к. на каждом шаге мы корректно вычисляем волнистые числа, то нет необходимости знать всё число: все зависит от последней цифры.
Следовательно, можно составить рекуррентную формулу, которая будет корректно вычислять количество n -значных волнистых чисел третьего типа начинающихся на цифру k 1 и заканчивающихся на цифру k 2.
Рассмотрим рекуррентную формулу для волнистых чисел третьего типа.
Начальные её значения  , т.е. есть только по одному однозначному волнистому числу, начинающемуся на i и заканчивающемуся на i (
, т.е. есть только по одному однозначному волнистому числу, начинающемуся на i и заканчивающемуся на i ( ).
).
Пусть  , тогда по остатку от деления i -2 на 4 определяем текущий знак: ”
, тогда по остатку от деления i -2 на 4 определяем текущий знак: ”  ", ”<”, ”>", ”
", ”<”, ”>", ”  ”:
”:
Если (i- 2) mod 4=0,  является суммой всех количеств i -1-значные волнистых чисел третьего типа, которые начинаются на k 1 и у которых последняя цифра меньше либо равна k 2.
является суммой всех количеств i -1-значные волнистых чисел третьего типа, которые начинаются на k 1 и у которых последняя цифра меньше либо равна k 2.
Если (i- 2) mod 4=1, 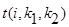 является суммой всех количеств i -1-значные волнистых чисел третьего типа, которые начинаются на k 1 и у которых последняя цифра меньше k 2.
является суммой всех количеств i -1-значные волнистых чисел третьего типа, которые начинаются на k 1 и у которых последняя цифра меньше k 2.
Если (i- 2) mod 4=2,  является суммой всех количеств i -1-значные волнистых чисел третьего типа, которые начинаются на k 1 и у которых последняя цифра больше.
является суммой всех количеств i -1-значные волнистых чисел третьего типа, которые начинаются на k 1 и у которых последняя цифра больше.
Если (i- 2) mod 4=3,  является суммой всех количеств i -1-значные волнистых чисел третьего типа, которые начинаются на k 1 и у которых последняя цифра больше либо равна k 2.
является суммой всех количеств i -1-значные волнистых чисел третьего типа, которые начинаются на k 1 и у которых последняя цифра больше либо равна k 2.
Аналогично, выводится рекуррентное соотношение для волнистых чисел четвертого типа.
Теорема 2. Количество n -значных волнистых чисел третьего типа:
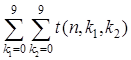
и количество n -значных волнистых чисел четвертого типа:
 .
.
Составим таблицу некоторых значений t (n, k, k 2)
| k
| 
| 
| 
| 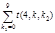
| 
|
| 0
| 1
| 0
| 0
| 0
| 0
|
| 1
| 1
| 9
| 36
| 240
| 990
|
| 2
| 1
| 8
| 28
| 196
| 826
|
| 3
| 1
| 7
| 21
| 154
| 665
|
| 4
| 1
| 6
| 15
| 115
| 510
|
| 5
| 1
| 5
| 10
| 80
| 365
|
| 6
| 1
| 4
| 6
| 50
| 235
|
| 7
| 1
| 3
| 3
| 26
| 126
|
| 8
| 1
| 2
| 1
| 9
| 45
|
| 9
| 1
| 1
| 0
| 0
| 0
|
| 
| 10
| 45
| 120
| 870
| 3762
|
| k
| 
| 
| 
| 
|
| 0
| 0
| 0
| 0
| 0
|
| 1
| 7722
| 28182
| 190740
| 796521
|
| 2
| 6412
| 23310
| 157926
| 659835
|
| 3
| 5131
| 18564
| 125922
| 526449
|
| 4
| 3906
| 14053
| 95449
| 399334
|
| 5
| 2771
|
|
|
|



 . Допустим, что i >
. Допустим, что i > 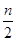 (т.е. j = n - i <
(т.е. j = n - i <  волнистым числом первого типа, если
волнистым числом первого типа, если



 волнистым числом третьего типа, если
волнистым числом третьего типа, если



 и
и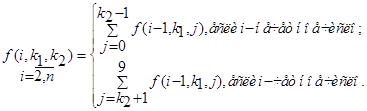
 и
и
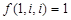 , т.е. есть только по одному однозначному волнистому числу, начинающемуся на i и заканчивающемуся на i (
, т.е. есть только по одному однозначному волнистому числу, начинающемуся на i и заканчивающемуся на i ( ).
). , тогда по четности/нечетности i (
, тогда по четности/нечетности i ( ) определяем текущий знак “<” или “>”:
) определяем текущий знак “<” или “>”: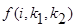 является суммой всех количеств i -1-значные волнистых чисел первого типа, которые начинаются на k 1 и у которых последняя цифра меньше k 2.
является суммой всех количеств i -1-значные волнистых чисел первого типа, которые начинаются на k 1 и у которых последняя цифра меньше k 2. является суммой всех количеств i -1-значные волнистых чисел первого типа, которые начинаются на k 1 и у которых последняя цифра больше k 2.
является суммой всех количеств i -1-значные волнистых чисел первого типа, которые начинаются на k 1 и у которых последняя цифра больше k 2.
 .
.







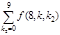



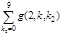




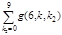






 и
и
 и
и 
 ", ”<”, ”>", ”
", ”<”, ”>", ”  ”), дописывается каждому числу цифра, меньшая, равная или большая последней, т.е. чтобы найти количество n -значных волнистых чисел, заканчивающихся на k, надо найти сумму всех количеств n -1-значных чисел заканчивающихся на цифры от 0 до k, или от 0 до k +1, или от k +1 до 9, или от k до 9.Т. к. на каждом шаге мы корректно вычисляем волнистые числа, то нет необходимости знать всё число: все зависит от последней цифры.
”), дописывается каждому числу цифра, меньшая, равная или большая последней, т.е. чтобы найти количество n -значных волнистых чисел, заканчивающихся на k, надо найти сумму всех количеств n -1-значных чисел заканчивающихся на цифры от 0 до k, или от 0 до k +1, или от k +1 до 9, или от k до 9.Т. к. на каждом шаге мы корректно вычисляем волнистые числа, то нет необходимости знать всё число: все зависит от последней цифры. , т.е. есть только по одному однозначному волнистому числу, начинающемуся на i и заканчивающемуся на i (
, т.е. есть только по одному однозначному волнистому числу, начинающемуся на i и заканчивающемуся на i ( ).
). , тогда по остатку от деления i -2 на 4 определяем текущий знак: ”
, тогда по остатку от деления i -2 на 4 определяем текущий знак: ”  ", ”<”, ”>", ”
", ”<”, ”>", ”  ”:
”: является суммой всех количеств i -1-значные волнистых чисел третьего типа, которые начинаются на k 1 и у которых последняя цифра меньше либо равна k 2.
является суммой всех количеств i -1-значные волнистых чисел третьего типа, которые начинаются на k 1 и у которых последняя цифра меньше либо равна k 2.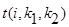 является суммой всех количеств i -1-значные волнистых чисел третьего типа, которые начинаются на k 1 и у которых последняя цифра меньше k 2.
является суммой всех количеств i -1-значные волнистых чисел третьего типа, которые начинаются на k 1 и у которых последняя цифра меньше k 2. является суммой всех количеств i -1-значные волнистых чисел третьего типа, которые начинаются на k 1 и у которых последняя цифра больше.
является суммой всех количеств i -1-значные волнистых чисел третьего типа, которые начинаются на k 1 и у которых последняя цифра больше.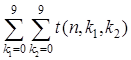
 .
.