

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...
Топ:
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Интересное:
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
1-го порядка
2.1. Дифференциальные уравнения с разделяющимися переменными.
Дифференциальное уравнение вида
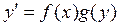 (4)
(4)
называется дифференциальным уравнением с разделяющимися переменными. Отличительной особенностью уравнений этого типа является то, что в правой их части находится произведение функций 
 одна из которых зависит только от x, другая только от y.
одна из которых зависит только от x, другая только от y.
Для того, чтобы найти решение уравнения (4), нужно разделить переменные x и y, собрав в левой и правой его частях функции, зависящие только от одной переменной.
Для разделения переменных в уравнении (4) заменим 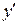 на
на 
и умножим обе части уравнения на 

Получили уравнение с разделенными переменными. Общий интеграл этого уравнения, а следовательно, и уравнения (4) находится почленным интегрированием:

где С – произвольная постоянная.
Таким образом, чтобы найти общее решение или общий интеграл уравнения (4), нужно разделить переменные x и y и почленно проинтегрировать полученное равенство.
Пример 1. Решить дифференциальное уравнение: 
Решение. Сравнивая данное уравнение с уравнением (4), замечаем, что оно является уравнением с разделяющимися переменными. Заменим 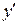 на
на 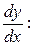
 Разделим переменные, умножая обе части уравнения на
Разделим переменные, умножая обе части уравнения на 
 .
.
Интегрируя полученное равенство, получим:

Отсюда  – общий интеграл данного уравнения. Разрешая его относительно у, можно записать общее решение данного уравнения в виде
– общий интеграл данного уравнения. Разрешая его относительно у, можно записать общее решение данного уравнения в виде

Ответ: 
З а м е ч а н и е. Уравнение вида
 (5)
(5)
также является уравнением с разделяющимися переменными, т.к. здесь коэффициенты при dx и dy являются произведениями функций, каждая из которых зависит только от одной переменной. Уравнение вида (5) решается тем же способом, что и уравнение (4).
|
|
2.2. Линейные дифференциальные уравнения 1-го порядка.
Дифференциальное уравнение вида
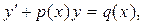 (6)
(6)
где 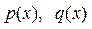 – заданные функции, называется линейным дифференциальным уравнением 1-го порядка.
– заданные функции, называется линейным дифференциальным уравнением 1-го порядка.
Отличительной особенностью линейного уравнения (6) является то, что искомая функция y и ее первая производная 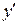 входят в уравнение в первых степенях и не перемножаются между собой, т.е. связаны линейно.
входят в уравнение в первых степенях и не перемножаются между собой, т.е. связаны линейно.
Для решения уравнения (6) воспользуемся способом подстановки. Будем искать неизвестную функцию y в виде произведения двух тоже пока неизвестных функций, т.е. положим  Тогда
Тогда  Подставив значения y и
Подставив значения y и  в уравнение (6), получим:
в уравнение (6), получим:  или
или
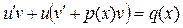 (7)
(7)
Если выбрать 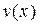 так, чтобы выражение, стоящее в скобках, обратилось в нуль, т.е.
так, чтобы выражение, стоящее в скобках, обратилось в нуль, т.е.
 , (8)
, (8)
то вторая функция  должна удовлетворять уравнению
должна удовлетворять уравнению
 (9)
(9)
Таким образом, решение линейного дифференциального уравнения (6) сводится к решению двух уравнений с разделяющимися переменными (8) и (9). Общее решение уравнения (6) есть произведение какого-либо частного решения уравнения (8) и общего решения уравнения (9):
 (10)
(10)
Пример 2. Найти решение дифференциального уравнения 
которое удовлетворяет условию 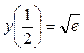 (задача Коши).
(задача Коши).
Решение.Разделив все члены уравнения на х, перепишем уравнение в виде
 Сравнивая его с уравнением (6), убеждаемся, что оно является линейным дифференциальным уравнением. Положим
Сравнивая его с уравнением (6), убеждаемся, что оно является линейным дифференциальным уравнением. Положим 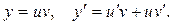 Подставив y и
Подставив y и  в уравнение, получим:
в уравнение, получим:  , или
, или
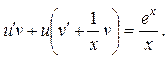 (*)
(*)
|
|
Найдем функцию  решая уравнение
решая уравнение 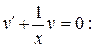

(в данном случае удобно использовать логарифмическую константу интегрирования: не С, а  ).
).
Из последнего уравнения получаем:
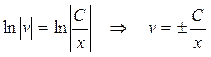 – общее решение, а при соответствующем подборе
– общее решение, а при соответствующем подборе  получаем
получаем  – частное решение уравнения
– частное решение уравнения  .
.
Подставим найденную функцию 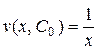 в уравнение (*):
в уравнение (*):  и найдем функцию
и найдем функцию  – общее решение этого уравнения.
– общее решение этого уравнения. 
 ,
,
откуда
 – общее решение уравнения
– общее решение уравнения  .
.
Общим решением исходного уравнения является функция
 .
.
Найдем частное решение, удовлетворяющее заданному начальному условию 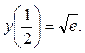 Для этого подставим в общее решение вместо x, y числа
Для этого подставим в общее решение вместо x, y числа  соответственно:
соответственно: 
Подставляя найденное значение С в общее решение, получим искомое частное решение (решение задачи Коши): 
Ответ: 
2.3. Уравнения Бернулли.
Дифференциальное уравнение вида
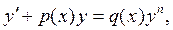 (11)
(11)
где n – действительное число,  , называется уравнением Бернулли.
, называется уравнением Бернулли.
Уравнение Бернулли является обобщением линейного дифференциального уравнения (6) и может быть решено тем же способом.
Пример решения уравнения Бернулли приведен в образце выполнения контрольной работы.
2.4.Однородные уравнения.
Функция f (x, y) называется однородной измерения m, если
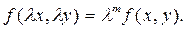
Дифференциальное уравнение вида
P (x,y) dx+Q (x,y) dy = 0 (12)
называется однородным, если P (x, y) и Q (x, y) – однородные функции одного измерения.
Однородное дифференциальное уравнение может быть приведено к виду
 (13)
(13)
С помощью подстановки  , т.е. y = tx однородное дифференциальное уравнение приводится к уравнению с разделяющимися переменными относительно новой неизвестной функции t (x).
, т.е. y = tx однородное дифференциальное уравнение приводится к уравнению с разделяющимися переменными относительно новой неизвестной функции t (x).
Пример 3. Решить дифференциальное уравнение: 
Решение. Здесь 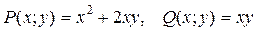 , обе функции – однородные, 2-го измерения, т.к. выполнено
, обе функции – однородные, 2-го измерения, т.к. выполнено
 .
.
Разрешим это уравнение относительно  . Для этого запишем его в виде
. Для этого запишем его в виде 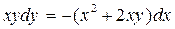 и разделим обе части на xydx, заменяя при этом
и разделим обе части на xydx, заменяя при этом  на
на 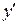 :
:  .
.
Введем подстановку y = tx, откуда  . Тогда уравнение примет вид:
. Тогда уравнение примет вид:

Это дифференциальное уравнение с разделяющимися переменными относительно новой неизвестной функции t (х). Разделяем переменные t и х:

Переходим к интегрированию:

Здесь использовано:

Поскольку функцию y (x) сложно выразить явным образом через х и С, запишем решение в форме общего интеграла уравнения.
|
|
Ответ:  – общий интеграл уравнения.
– общий интеграл уравнения.
|
|
|

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!