МАТЕМАТИКА
Методические рекомендации по организации и выполнению расчетно-графической работы № 2 для студентов ИДО, направления подготовки 20.03.01 Техносферная безопасность, профиль подготовки Пожарная безопасность
Тюмень, 2017
УДК
ББК
Составитель: доцент кафедры математики и информатики М.В. Виноградова
Математика. Методические указания и варианты расчетно-графической работы для студентов института дистанционного образования направления подготовки 20.03.01 Техносферная безопасность профиль Пожарная безопасность / М.В. Виноградова– Тюмень, 2017 – 78 с. –электронный ресурс
Рецензент:
Н.Н. Мальчукова– к.п.н., доцент кафедры математики и информатики ГАУ Северного Зауралья
УТВЕРЖДЕНО
на заседании кафедры математики и информатики
протокол № … от …..2017 г.
методической комиссией механико-технологического института
протокол № … от …..2017 г.
© ГАУ Северного Зауралья, 2017
© М.В. Виноградова, 2017
ОГЛАВЛЕНИЕ
| Выполнение и оформление контрольных работ
|
|
| РАЗДЕЛ I.
| ИНТЕГРАЛЬНОЕ ИСЧЕСЛЕНИЕ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
|
|
| Глава 1.
| НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
|
|
| 1.1.
| Первообразная функция и неопределенный интеграл
|
|
| 1. 2.
| Методы интегрирования
|
|
| Примеры решения типовых задач
|
|
| Глава 2.
| ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
|
|
| 2.1.
| Понятие определенного интеграла и его свойства
|
|
| 2.2.
| Геометрические приложения определённого интеграла
|
|
| Примеры решения типовых задач
|
|
| Глава 3.
| ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
|
|
| 3.1.
| Основные понятия и определения
|
|
| 3.2.
| Уравнения с разделяющимися переменными
|
|
| 3.3.
| Линейные уравнения первого порядка
|
|
| 33.4.
| Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
|
|
| Примеры решения типовых задач
|
|
| Контрольный тест после изучения раздела I «Интегральное исчисление и дифференциальные уравнения»
|
|
| РАЗДЕЛ II.
| РЯДЫ
|
|
| Глава 4.
| ЧИСЛОВЫЕ РЯДЫ
|
|
| 4.1.
| Основные понятия. Сходимость ряда. Необходимый признак сходимости
|
|
| 4.2.
| Ряды с положительными членами
|
|
| 4.3.
| Сходимость знакочередующихся рядов
|
|
| Глава 5.
| ФУНКЦИОНАЛЬНЫЕ РЯДЫ. СТЕПЕННЫЕ РЯДЫ
|
|
| 5.1.
| Область сходимости степенного ряда
|
|
| 5.2.
| Разложение функций в степенные ряды
|
| 5.3.
| Применение степенных рядов в приближенных вычислениях
|
|
| Примеры решения типовых задач
|
|
| Контрольный тест после изучения раздела II «Ряды»
|
|
| Задания для расчетно-графической работы № 2
|
|
| Вопросы для подготовки к экзамену
|
|
| Учебно-методическое и информационное обеспечение дисциплины
|
|
| | | | | | | | |
Выполнение и оформление контрольных работ
1. Слушатели выполняют контрольную работу в соответствии с учебным планом в сроки, установленные ИДО.
2. Каждая контрольная работа выполняется в отдельной тетради в клеточку, ручкой любого цвета, кроме зеленого и красного, аккуратно и разборчивым почерком, чертежи выполняются простым карандашом с использованием инструмента.
3. На титульном листе следует указать фамилию, имя, отчество слушателя, его адрес с указанием почтового индекса, номер зачетной книжки, номер варианта.
4. Задания в контрольных работах выполняются по порядку, согласно расположению их в варианте.
5. На заключительном листе контрольных работ следует указать список литературы, которым Вы пользовались при их выполнении.
6. Если контрольные работы выполнены с нарушением всех вышеперечисленных указаний или не полностью, то они возвращаются слушателю для доработки без проверки.
7. Если работы не зачтены, внимательно изучите все замечания рецензента. Переделайте работы в соответствии с рекомендациями рецензента.
8. Переделанные работы предоставляются на проверку вместе с незачтенными работами.
9. Слушатель выполняет тот вариант контрольных работ, который совпадает с последней цифрой его учебного шифра.
При этом если предпоследняя цифра учебного шифра – нечетное число (1,3,5,7,9),то номера задач для соответствующего варианта даны в таблице № 1; если же предпоследняя цифра учебного шифра – четное число или ноль (2,4,6,8,0), то номера задач для соответствующего варианта даны в таблице № 2.
Таблица № 1.
| № варианта
| Номера заданий для контрольной работы № 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица № 2.
| № варианта
| Номера заданий для контрольной работы № 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
РАЗДЕЛ I. ИНТЕГРАЛЬНОЕ ИСЧЕСЛЕНИЕ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Глава 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Таблица основных интегралов
| Интеграл
| Значение
| Интеграл
| Значение
|
|
| 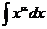
| 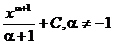
|
| 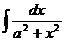
| 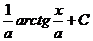
|
|
| 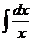
| 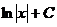
|
| 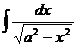
| arcsin  + C + C
|
|
| 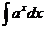
| 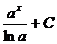
|
| 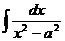
| 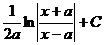
|
|
| 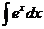
| ex + C
|
| 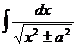
| ln 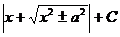
|
|
| 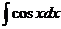
| sinx + C
|
| 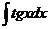
| -ln½cosx½+С
|
|
| 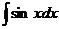
| -cosx + C
|
| 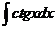
| ln½sinx½+ C
|
|
| 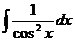
| tgx + C
|
| 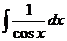
| 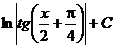
|
|
| 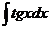 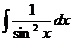
| -ctgx + C
|
| 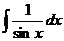
| 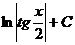
|
Методы интегрирования
1. Непосредственное интегрирование. Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием.
Пример.
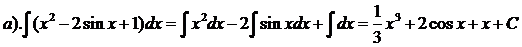
Проверка:
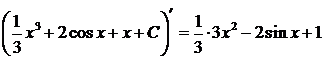
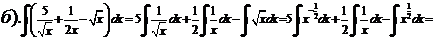
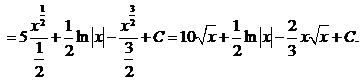
Проверка:
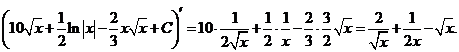
2. Способ подстановки (замены переменных). Если требуется найти интеграл 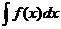 , но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
, но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
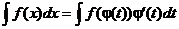
Пример.
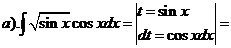
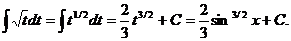
Проверка:
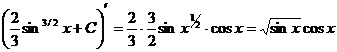
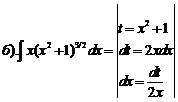
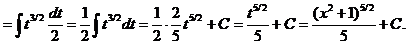
Проверка:
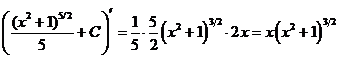
Интегрирование по частям
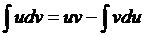
Формула интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Замечание: Если в подынтегральной функции имеется множитель вида 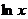 ,
, 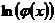 ,
, 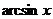 ,
, 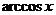 ,
, 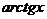 ,
, 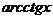 , то их удобно принимать в качестве
, то их удобно принимать в качестве 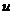 , так как они легче дифференцируются.
, так как они легче дифференцируются.
Если подынтегральная функция имеет вид 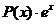 ,
, 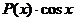 ,
, 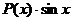 ,
, 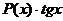 ,
, 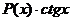 , то за
, то за 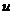 удобно принимать
удобно принимать 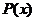 , где
, где 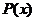 - это некоторый многочлен, причем формулу интегрирования по частям необходимо применять столько раз, какова степень многочлена.
- это некоторый многочлен, причем формулу интегрирования по частям необходимо применять столько раз, какова степень многочлена.
Пример.
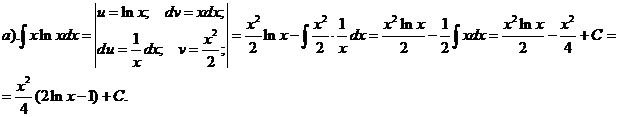 Проверка:
Проверка:
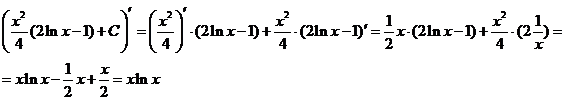
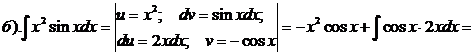
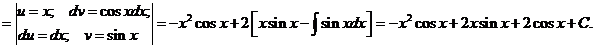 Проверка:
Проверка:
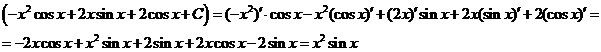
Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.
Примеры решения типовых задач
№ 1. Найти интеграл следующих функций:
а). 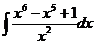 б).
б). 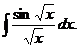 в).
в). 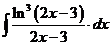 г).
г). 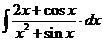
д). 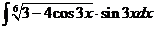 е).
е). 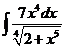 ж).
ж). 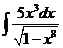 з).
з). 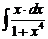
и).  к).
к). 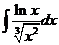 л).
л). 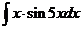 м).
м). 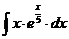 н).
н). 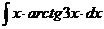
Решение:
а). 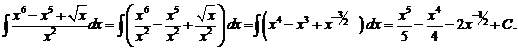
б) Воспользуемся подстановкой x=t2. Тогда 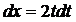 , получим:
, получим:
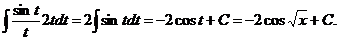
в). Если под интегралом содержится логарифмическая функция, то удобно принять ее за новую переменную, если под знаком интеграла присутствует производная этой функции (с точностью до постоянного множителя).
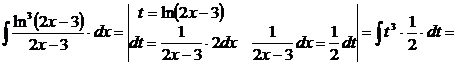
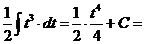
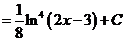
г). 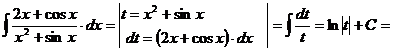

д). За новую переменную удобно взять подкоренное выражение, если под интегралом присутствует также его производная с точностью до постоянного множителя.
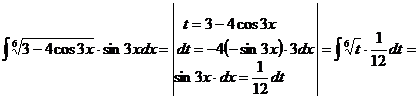
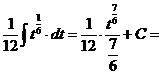
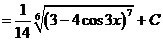
е). 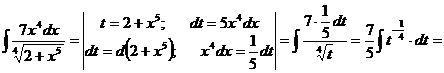
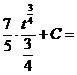
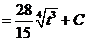
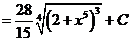
ж). Новая переменная иногда выбирается из следующих соображений: в знаменателе стоит разность постоянной и квадрата некоторой функции. Эту функцию мы принимаем за новую переменную, если в числителе присутствует ее производная (с точностью до постоянного множителя).
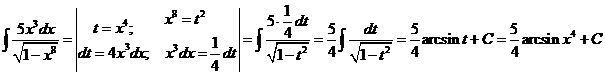 з). Подстановка выбирается аналогично предыдущему примеру.
з). Подстановка выбирается аналогично предыдущему примеру.
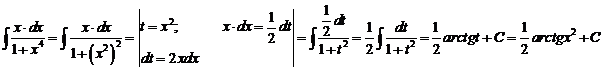
и). За новую переменную иногда выбирают функцию, стоящую в основании степени, если подынтегральное выражение содержит производную этой функции с точностью до постоянного множителя. 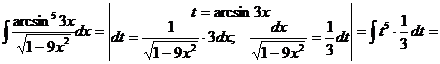
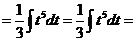
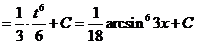
к). 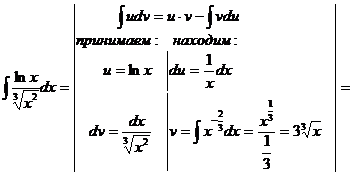
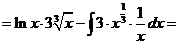
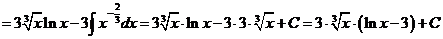
л). 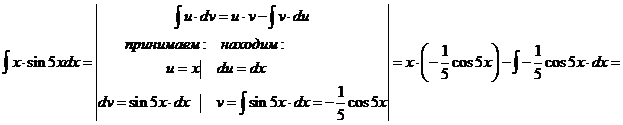

м). 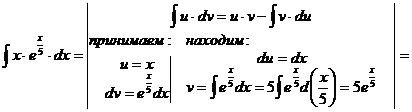
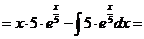
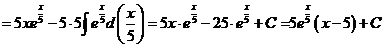
н). 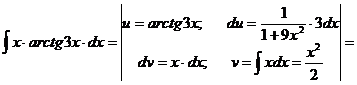
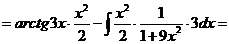
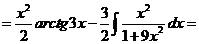
Чтобы взять последний интеграл, умножим и разделим числитель на 9, затем вчислителе прибавим иотнимем единицу, после чего разобьем интеграл на два табличных:
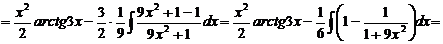
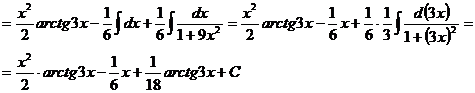
Формула Ньютона-Лейбница
Если функция f(x) непрерывна на отрезке  и F(x) – первообразная функции f(x) на этом отрезке, то:
и F(x) – первообразная функции f(x) на этом отрезке, то:

Эта формула называется формулой Ньютона-Лейбница.
При вычислении интегралов ее часто записывают в виде

Пример.
 =
= 
Замечания.
 1. Если же
1. Если же  на
на  , то – f(х)
, то – f(х)  на этом отрезке. Поэтому площадь S соответствующей криволинейной трапеции находится по формуле:
на этом отрезке. Поэтому площадь S соответствующей криволинейной трапеции находится по формуле:

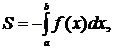 или
или 
Наконец, если линия y=f(x) пересекает ось Ох, то отрезок  надо разбить на части, в пределах которых f(x) не меняет знака, и к каждой части применить ту из формул, которая ей соответствует.
надо разбить на части, в пределах которых f(x) не меняет знака, и к каждой части применить ту из формул, которая ей соответствует.
 2. Площадь криволинейной фигуры, ограниченной сверху графиком функции y2=f2(x), снизу – графиком функции y1=f1(x), слева и справа прямыми x=a, x=b, вычисляется по формуле:
2. Площадь криволинейной фигуры, ограниченной сверху графиком функции y2=f2(x), снизу – графиком функции y1=f1(x), слева и справа прямыми x=a, x=b, вычисляется по формуле: 


 3. Площадь криволинейной фигуры, ограниченной справа графиком функции x2=j2(y), слева – графиком функции x1=j1(y), снизу и сверху прямыми y=c, y=d, вычисляется по формуле:
3. Площадь криволинейной фигуры, ограниченной справа графиком функции x2=j2(y), слева – графиком функции x1=j1(y), снизу и сверху прямыми y=c, y=d, вычисляется по формуле: 
Пример. Найти площадь плоской фигуры, ограниченной графиком функции y = sin x и осью абсцисс при условии  .
.
Решение:
Разобьём отрезок  на два отрезка:
на два отрезка:  и
и  . На первом из них sin x
. На первом из них sin x  , на втором sin x
, на втором sin x 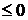 . Тогда, используя формулы, находим искомую площадь:
. Тогда, используя формулы, находим искомую площадь:
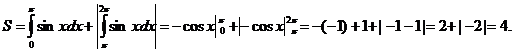

Примеры решения типовых задач
№1. Вычислить площадь фигуры, ограниченной линиями  и
и 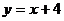 .
.
Решение:
1. Найдем пределы интегрирования, в качестве  и
и 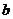 возьмем абсциссы точек пересечения данных линий.
возьмем абсциссы точек пересечения данных линий.
Для их нахождения решим систему уравнений:


 ;
;
 ;
;
 ,
, 
 2. Определим, какой график расположен выше. Для этого построим заданные линии. Графиком функции
2. Определим, какой график расположен выше. Для этого построим заданные линии. Графиком функции  является парабола. Найдем координаты вершины параболы:
является парабола. Найдем координаты вершины параболы:
 ,
,  .
.
Найдем точку пересечения параболы с осями координат:
 ,
, 
 ,
, 
 и
и  .
.
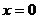 ,
, 
 .
.
Получили две точки пересечения с осью  :
:  и
и  .
.
Графиком функции 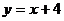 является прямая линия, для построения которой достаточно взять две точки.
является прямая линия, для построения которой достаточно взять две точки.
Из рисунка видно, что график функции 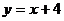 находится выше графика функции
находится выше графика функции  , следовательно, выполняется условие
, следовательно, выполняется условие  .
.
Применяя формулу (2), найдем площадь фигуры, ограниченной заданными линиями:
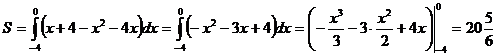 (кв.ед.)
(кв.ед.)
№2. Вычислить объем тела, полученного вращением вокруг оси  криволинейной трапеции, ограниченной гиперболой
криволинейной трапеции, ограниченной гиперболой  , прямыми
, прямыми 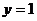 ,
,  и осью Оу.
и осью Оу.
Решение:  ,
,  ,
,  . Тогда
. Тогда  .
.
Решение.
 ; Разделяем переменные
; Разделяем переменные 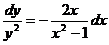 .
.
Интегрируем обе части последнего равенства
 .
.
В результате получим:  .
.
Таким образом, получаем общий интеграл:  .
.
Находим частное решение уравнения. Подставляем начальное условие:
 .
.
Отсюда получаем частный интеграл  .
.
Примеры решения типовых задач
№ 1. Найти общее решение дифференциального уравнения  и частное решение, удовлетворяющее начальному условию y(0)=2.
и частное решение, удовлетворяющее начальному условию y(0)=2.
Решение:
Данное уравнение является линейным, так как содержит искомую функцию и ее производную в первой степени и не содержит их произведений. Применяем подстановку y=uv.
Если y=uv, то  . Подставляя y и y’ в исходное уравнение, получим
. Подставляя y и y’ в исходное уравнение, получим  . Группируем первое и третье слагаемые и выносим v за скобку
. Группируем первое и третье слагаемые и выносим v за скобку

 (1).
(1).
Так как искомая функция y представлена в виде произведения двух других неизвестных функций, то одну из них можно выбрать произвольно. Выберем функцию u так, чтобы выражение, стоящее в скобках левой части равенства (1), обращалось в нуль, то есть, чтобы имело место равенство  (2).
(2).
Тогда уравнение (1) принимает вид:  (3).
(3).
Уравнение (2) является уравнением с разделяющимися переменными относительно u и x. Решим его

Чтобы равенство (2) имело место, достаточно найти одно какое-либо частное решение, удовлетворяющее этому уравнению. Поэтому для простоты при интегрировании этого уравнения находим то частное решение, которое соответствует значению произвольной постоянной С=0. Подставив в (3) найденное выражение для u, получим

Интегрируя, имеем 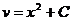 .
.
Теперь можно получить общее решение исходного уравнения  .
.
Определим значение произвольной постоянной С при указанных начальных условиях
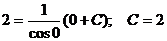 .
.
Таким образом,  есть частное решение, удовлетворяющее данному начальному условию.
есть частное решение, удовлетворяющее данному начальному условию.
№ 2. Найти общее и частное решение дифференциального уравнения второго порядка с постоянными коэффициентами
 .
.  ,
,  .
.
Решение:
Составим характеристическое уравнение:
 ;
; 
 и
и  .
.
Тогда, общее решение дифференциального уравнения будет иметь вид
 .
.
Найдем  :
:
 .
.
Подставим начальные значения в выражения  и
и  , получим систему двух уравнений с двумя неизвестными
, получим систему двух уравнений с двумя неизвестными  и
и  .
.



 .
.
 - частное решение.
- частное решение.
РАЗДЕЛ II. РЯДЫ
Глава 4. ЧИСЛОВЫЕ РЯДЫ
Основные понятия. Сходимость ряда. Необходимый признак сходимости
Определение. Числовым рядом называется бесконечная последовательность чисел  , соединенных знаком сложения, то есть
, соединенных знаком сложения, то есть
 (13.1)
(13.1)
где числа  называются членами ряда,
называются членами ряда,  - общим членом ряда.
- общим членом ряда.
Ряд (13.1) считается заданным, если известен его общий член  .
.
Пример.
1) 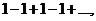
2) 
3) 
Ряд можно задать с помощью общего члена, например,  определяет следующий ряд:
определяет следующий ряд: 
Определение. Частичной суммой  числового ряда называетсясуммаего первых n членов,
числового ряда называетсясуммаего первых n членов,

Определение. Суммой числового ряда S называется предел последовательности его частичных сумм, если этот предел существует
 ,
,
причем ряд называется сходящимся, в противном случае, если же  не существует, или
не существует, или  то ряд называется расходящимся.
то ряд называется расходящимся.
Пример. Исследовать на сходимость ряды
а). 
б). 
Решение:
а). Рассмотрим ряд  . Найдем его частичные суммы
. Найдем его частичные суммы 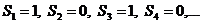 Последовательность его частичных сумм 1,0,1,0.1,0... не имеет предела, следовательно ряд расходится.
Последовательность его частичных сумм 1,0,1,0.1,0... не имеет предела, следовательно ряд расходится.
б). Рассмотрим ряд

найдем его частичные суммы:
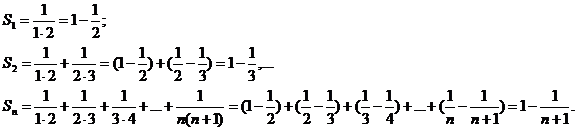
Так как  то рассматриваемый ряд сходится: его сумма равна 1.
то рассматриваемый ряд сходится: его сумма равна 1.
Решение.
Сравним данный ряд с гармоническим рядом  , про который известно, что он расходится.
, про который известно, что он расходится.
Так как  , то по теореме 2, из расходимости ряда с меньшими членами следует расходимость ряда с большими членами, делаем вывод, что ряд
, то по теореме 2, из расходимости ряда с меньшими членами следует расходимость ряда с большими членами, делаем вывод, что ряд  расходится.
расходится.
Теорема (предельный признак сравнения). Если  и
и  - ряды с положительными членами и существует конечный предел отношения их общих членов, то есть
- ряды с положительными членами и существует конечный предел отношения их общих членов, то есть  , то ряды будут вести себя одинаково, то есть либо сходиться, либо расходиться.
, то ряды будут вести себя одинаково, то есть либо сходиться, либо расходиться.
Пример. Исследовать на сходимость ряд  .
.
Решение:
Сравним данный ряд с расходящимся гармоническим рядом  .
.
 ;
; 
Тогда  , следовательно, ряды ведут себя одинаково, то есть данный ряд расходится.
, следовательно, ряды ведут себя одинаково, то есть данный ряд расходится.
Теорема (признак Даламбера). Пусть для ряда  с положительными членами существует предел отношения последующего члена ряда
с положительными членами существует предел отношения последующего члена ряда  к предыдущему
к предыдущему  , то есть
, то есть
 .
.
Тогда, если  , то ряд сходится, если
, то ряд сходится, если  , то ряд расходится, если
, то ряд расходится, если  , то вопрос о сходимости ряда остается открытым, необходимо использование иных признаков сходимости.
, то вопрос о сходимости ряда остается открытым, необходимо использование иных признаков сходимости.
Пример. Исследовать на сходимость ряд  .
.
Решение:  ;
;  .
.
 , следовательно, ряд сходится.
, следовательно, ряд сходится.
Теорема (радикальный признак сравнения). Если для ряда  существует предел
существует предел  , то при r<1 ряд сходится, а при r>1 ряд расходится, при r=1 ответ остается открытым.
, то при r<1 ряд сходится, а при r>1 ряд расходится, при r=1 ответ остается открытым.
Пример. Определить сходимость ряда  .
.
Решение:
 .Следовательно, ряд сходится.
.Следовательно, ряд сходится.
Теорема (интегральный признак сравнения). Если f(x) при x ³ 1-непрерывная положительная и монотонно убывающая функция, то  , где an = f(n) сходится или расходится, в зависимости от того сходится или расходится несобственный интеграл
, где an = f(n) сходится или расходится, в зависимости от того сходится или расходится несобственный интеграл  .
.
Пример. Исследовать на сходимость обобщенный гармонический ряд
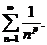
Решение:
Члены ряда составляют монотонно убывающую последовательность  .
.
Следовательно, функцией 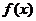 будет
будет 
Тогда  (доказать самостоятельно).
(доказать самостоятельно).
Если p=1, то имеем  – гармонический ряд, который расходится.
– гармонический ряд, который расходится.
Итак, ряд  сходится при
сходится при  и расходится при
и расходится при  .
.
Признак Лейбница
Если члены знакочередующегося ряда убывают по абсолютной величине, то есть  и предел его общего члена при
и предел его общего члена при 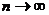 равен 0, то есть
равен 0, то есть  , то ряд сходится, а его сумма не превосходит первого члена, то есть
, то ряд сходится, а его сумма не превосходит первого члена, то есть  . Если нарушается хотя бы одно из этих условий, то ряд расходится.
. Если нарушается хотя бы одно из этих условий, то ряд расходится.
Пример. Исследовать на сходимость ряд  .
.
Решение:
1) 
2)  .
.
Так как выполнены оба условия признака Лейбница, то ряд сходится.
Составим ряд из модулей 
Исследуем полученный ряд с общим членом  . По признаку сравнения (сравнивая с рядом Дирихле) ряд сходится, т.к. α.=2>1.
. По признаку сравнения (сравнивая с рядом Дирихле) ряд сходится, т.к. α.=2>1.
Таким образом, данный ряд сходится абсолютно.
Свойства степенных рядов
Рассмотрим степенной ряд  имеющий радиус сходимости
имеющий радиус сходимости 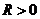 (
( может равняться
может равняться  ). Тогда каждому значению
). Тогда каждому значению  из интервала сходимости соответствует некоторая сумма ряда. Следовательно, сумма степенного ряда есть функция от
из интервала сходимости соответствует некоторая сумма ряда. Следовательно, сумма степенного ряда есть функция от  на интервале сходимости. Обозначим ее через
на интервале сходимости. Обозначим ее через  . Тогда можно записать равенство
. Тогда можно записать равенство  понимая его в том смысле, что сумма ряда в каждой точке
понимая его в том смысле, что сумма ряда в каждой точке  из интервала сходимости равна значению функции
из интервала сходимости равна значению функции  в этой точке. В этом же смысле будем говорить, что ряд сходится к функции
в этой точке. В этом же смысле будем говорить, что ряд сходится к функции  на интервале сходимости. Вне интервала сходимости равенство не имеет смысла.
на интервале сходимости. Вне интервала сходимости равенство не имеет смысла.
Для степенных рядов справедливы следующие утверждения:
1) Степенной ряд в интервале его сходимости можно почленно дифференцировать неограниченное число раз причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд а суммы их соответственно равны  .
.
2) Степенной ряд можно неограниченное число раз почленно интегрировать в пределах от 0 до  , если
, если  , причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны
, причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны

Примеры решения типовых задач
№ 1. Исследовать на сходимость ряды
а).  б).
б). 
в).  . г).
. г). 
Решение:
а). Применим признак Даламбера, вычислим
 число D=0 <1, следовательно, ряд сходится.
число D=0 <1, следовательно, ряд сходится.
б). Применим признак Коши:
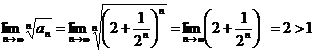 – ряд расходится.
– ряд расходится.
в). Имеем  следовательно,
следовательно,  - непрерывная, положительная и монотонно убывающая функция при x ≥ 1. Применим интегральный признак сходимости.
- непрерывная, положительная и монотонно убывающая функция при x ≥ 1. Применим интегральный признак сходимости.

Т.к. несобственный интеграл равен 1, следовательно сходится (является конечной величиной), поэтому сходится и данный ряд.
г). Ряд 
1) 
2). 
Так как выполнены оба условия признака Лейбница, то ряд сходится.
Составим ряд из модулей 
Исследуем полученный ряд с общим членом 
|
|
|



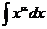
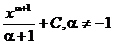
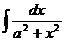
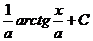
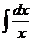
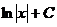
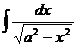
 + C
+ C
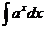
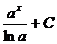
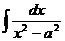
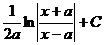
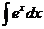
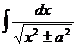
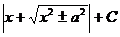
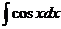
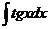
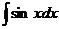
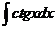
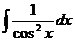
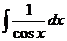
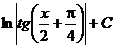
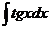
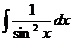
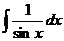
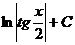
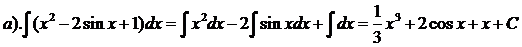
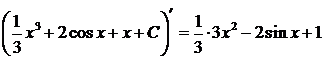
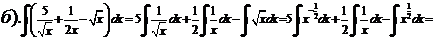
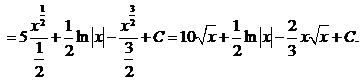
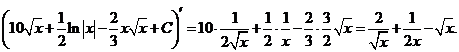
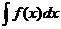 , но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
, но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается: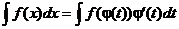
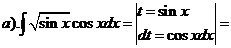
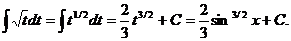
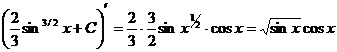
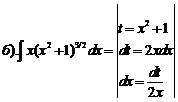
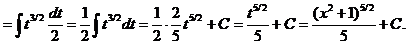
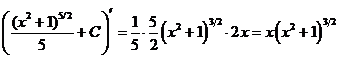
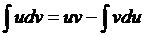
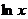 ,
, 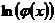 ,
, 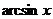 ,
, 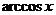 ,
, 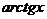 ,
, 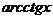 , то их удобно принимать в качестве
, то их удобно принимать в качестве 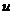 , так как они легче дифференцируются.
, так как они легче дифференцируются.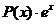 ,
, 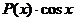 ,
, 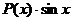 ,
, 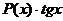 ,
, 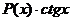 , то за
, то за 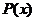 , где
, где 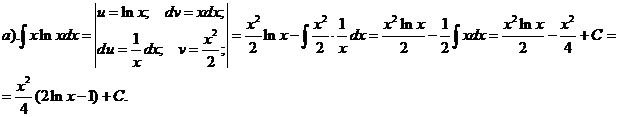 Проверка:
Проверка: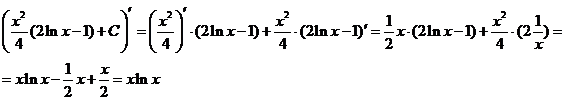
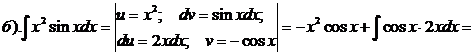
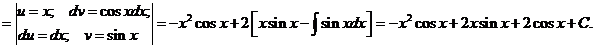 Проверка:
Проверка: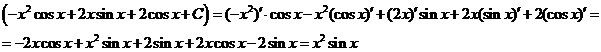
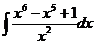 б).
б). 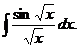 в).
в). 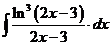 г).
г). 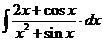
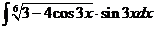 е).
е). 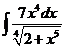 ж).
ж). 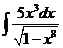 з).
з). 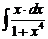
 к).
к). 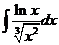 л).
л). 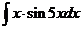 м).
м). 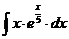 н).
н). 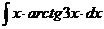
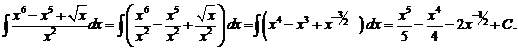
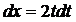 , получим:
, получим: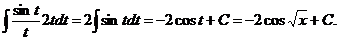
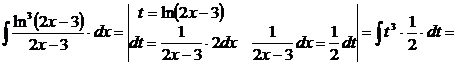
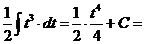
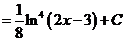
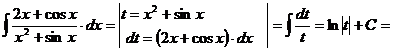

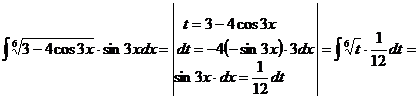
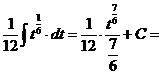
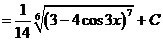
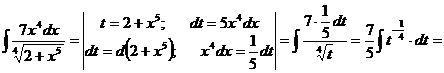
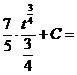
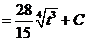
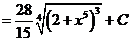
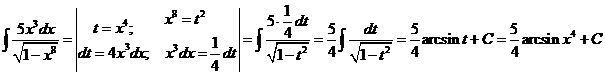 з). Подстановка выбирается аналогично предыдущему примеру.
з). Подстановка выбирается аналогично предыдущему примеру.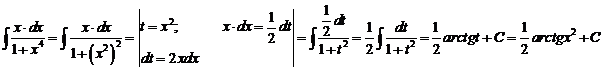
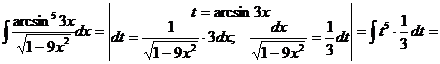
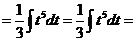
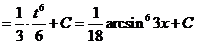
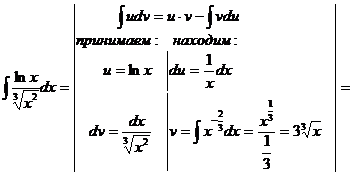
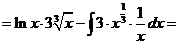
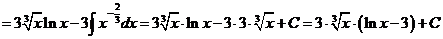
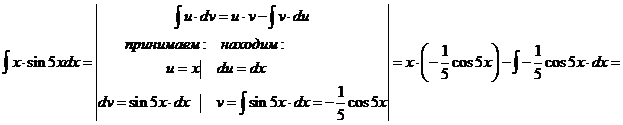

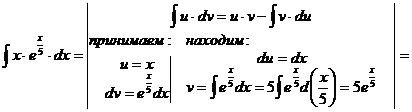
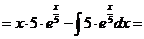
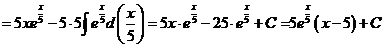
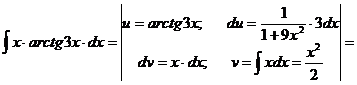
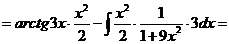
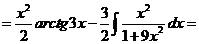
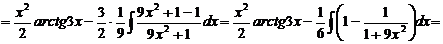
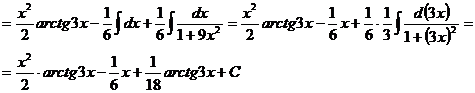
 и F(x) – первообразная функции f(x) на этом отрезке, то:
и F(x) – первообразная функции f(x) на этом отрезке, то:

 =
= 
 1. Если же
1. Если же  на
на  на этом отрезке. Поэтому площадь S соответствующей криволинейной трапеции находится по формуле:
на этом отрезке. Поэтому площадь S соответствующей криволинейной трапеции находится по формуле:
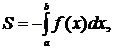 или
или 
 2. Площадь криволинейной фигуры, ограниченной сверху графиком функции y2=f2(x), снизу – графиком функции y1=f1(x), слева и справа прямыми x=a, x=b, вычисляется по формуле:
2. Площадь криволинейной фигуры, ограниченной сверху графиком функции y2=f2(x), снизу – графиком функции y1=f1(x), слева и справа прямыми x=a, x=b, вычисляется по формуле: 


 3. Площадь криволинейной фигуры, ограниченной справа графиком функции x2=j2(y), слева – графиком функции x1=j1(y), снизу и сверху прямыми y=c, y=d, вычисляется по формуле:
3. Площадь криволинейной фигуры, ограниченной справа графиком функции x2=j2(y), слева – графиком функции x1=j1(y), снизу и сверху прямыми y=c, y=d, вычисляется по формуле: 
 .
. на два отрезка:
на два отрезка:  и
и  . На первом из них sin x
. На первом из них sin x 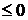 . Тогда, используя формулы, находим искомую площадь:
. Тогда, используя формулы, находим искомую площадь: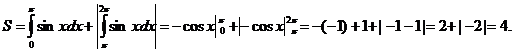

 и
и 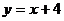 .
. и
и 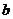 возьмем абсциссы точек пересечения данных линий.
возьмем абсциссы точек пересечения данных линий.

 ;
; ;
; ,
, 
 2. Определим, какой график расположен выше. Для этого построим заданные линии. Графиком функции
2. Определим, какой график расположен выше. Для этого построим заданные линии. Графиком функции  ,
,  .
. ,
, 
 ,
,  и
и  .
.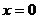 ,
,  :
:  и
и  .
. .
.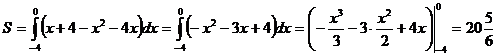 (кв.ед.)
(кв.ед.) криволинейной трапеции, ограниченной гиперболой
криволинейной трапеции, ограниченной гиперболой  , прямыми
, прямыми 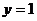 ,
,  и осью Оу.
и осью Оу. ,
,  ,
,  . Тогда
. Тогда  .
. ; Разделяем переменные
; Разделяем переменные 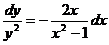 .
. .
. .
. .
. .
. .
. и частное решение, удовлетворяющее начальному условию y(0)=2.
и частное решение, удовлетворяющее начальному условию y(0)=2. . Подставляя y и y’ в исходное уравнение, получим
. Подставляя y и y’ в исходное уравнение, получим  . Группируем первое и третье слагаемые и выносим v за скобку
. Группируем первое и третье слагаемые и выносим v за скобку
 (1).
(1). (2).
(2). (3).
(3).

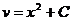 .
. .
.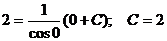 .
. есть частное решение, удовлетворяющее данному начальному условию.
есть частное решение, удовлетворяющее данному начальному условию. .
.  ,
,  .
. ;
; 
 и
и  .
. .
. :
: .
. и
и  и
и  .
.

 .
. - частное решение.
- частное решение. , соединенных знаком сложения, то есть
, соединенных знаком сложения, то есть (13.1)
(13.1) - общим членом ряда.
- общим членом ряда.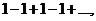


 определяет следующий ряд:
определяет следующий ряд: 
 числового ряда называетсясуммаего первых n членов,
числового ряда называетсясуммаего первых n членов,
 ,
, не существует, или
не существует, или  то ряд называется расходящимся.
то ряд называется расходящимся.

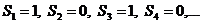 Последовательность его частичных сумм 1,0,1,0.1,0... не имеет предела, следовательно ряд расходится.
Последовательность его частичных сумм 1,0,1,0.1,0... не имеет предела, следовательно ряд расходится.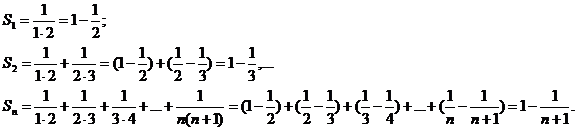
 то рассматриваемый ряд сходится: его сумма равна 1.
то рассматриваемый ряд сходится: его сумма равна 1. , про который известно, что он расходится.
, про который известно, что он расходится. , то по теореме 2, из расходимости ряда с меньшими членами следует расходимость ряда с большими членами, делаем вывод, что ряд
, то по теореме 2, из расходимости ряда с меньшими членами следует расходимость ряда с большими членами, делаем вывод, что ряд  расходится.
расходится. и
и  - ряды с положительными членами и существует конечный предел отношения их общих членов, то есть
- ряды с положительными членами и существует конечный предел отношения их общих членов, то есть  , то ряды будут вести себя одинаково, то есть либо сходиться, либо расходиться.
, то ряды будут вести себя одинаково, то есть либо сходиться, либо расходиться. .
. ;
; 
 , следовательно, ряды ведут себя одинаково, то есть данный ряд расходится.
, следовательно, ряды ведут себя одинаково, то есть данный ряд расходится. к предыдущему
к предыдущему  .
. , то ряд сходится, если
, то ряд сходится, если  , то ряд расходится, если
, то ряд расходится, если  , то вопрос о сходимости ряда остается открытым, необходимо использование иных признаков сходимости.
, то вопрос о сходимости ряда остается открытым, необходимо использование иных признаков сходимости. .
. ;
;  .
. , следовательно, ряд сходится.
, следовательно, ряд сходится. существует предел
существует предел  , то при r<1 ряд сходится, а при r>1 ряд расходится, при r=1 ответ остается открытым.
, то при r<1 ряд сходится, а при r>1 ряд расходится, при r=1 ответ остается открытым. .
. .Следовательно, ряд сходится.
.Следовательно, ряд сходится. , где an = f(n) сходится или расходится, в зависимости от того сходится или расходится несобственный интеграл
, где an = f(n) сходится или расходится, в зависимости от того сходится или расходится несобственный интеграл  .
.
 .
.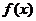 будет
будет 
 (доказать самостоятельно).
(доказать самостоятельно). – гармонический ряд, который расходится.
– гармонический ряд, который расходится. сходится при
сходится при  и расходится при
и расходится при  .
. и предел его общего члена при
и предел его общего члена при 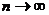 равен 0, то есть
равен 0, то есть  , то ряд сходится, а его сумма не превосходит первого члена, то есть
, то ряд сходится, а его сумма не превосходит первого члена, то есть  . Если нарушается хотя бы одно из этих условий, то ряд расходится.
. Если нарушается хотя бы одно из этих условий, то ряд расходится. .
.
 .
.
 . По признаку сравнения (сравнивая с рядом Дирихле) ряд сходится, т.к. α.=2>1.
. По признаку сравнения (сравнивая с рядом Дирихле) ряд сходится, т.к. α.=2>1. имеющий радиус сходимости
имеющий радиус сходимости 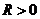 (
( может равняться
может равняться  ). Тогда каждому значению
). Тогда каждому значению  из интервала сходимости соответствует некоторая сумма ряда. Следовательно, сумма степенного ряда есть функция от
из интервала сходимости соответствует некоторая сумма ряда. Следовательно, сумма степенного ряда есть функция от  . Тогда можно записать равенство
. Тогда можно записать равенство  понимая его в том смысле, что сумма ряда в каждой точке
понимая его в том смысле, что сумма ряда в каждой точке  .
. , причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны
, причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны
 б).
б). 
 . г).
. г). 
 число D=0 <1, следовательно, ряд сходится.
число D=0 <1, следовательно, ряд сходится.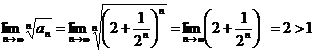 – ряд расходится.
– ряд расходится. следовательно,
следовательно,  - непрерывная, положительная и монотонно убывающая функция при x ≥ 1. Применим интегральный признак сходимости.
- непрерывная, положительная и монотонно убывающая функция при x ≥ 1. Применим интегральный признак сходимости.