1) Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0.
Пример:
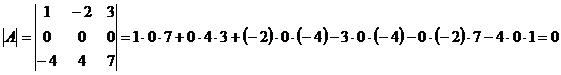 .
.
2) Если все элементы какой-либо строки (столбца) матрицы умножить на число 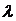 , то и определитель матрицы умножится на это число
, то и определитель матрицы умножится на это число 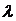 .
.
Замечание. За знак определителя можно выносить общий множитель элементов любой строки или столбца.
Примеры: 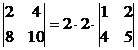 ;
;
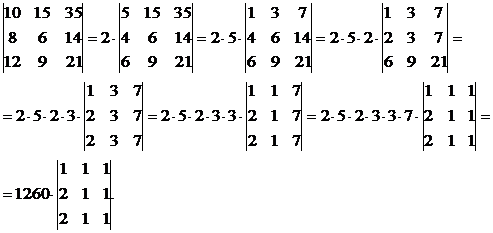
3) При транспонировании матрицы ее определитель не изменяется: 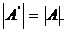
Пример:
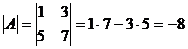 ;
; 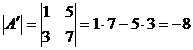 .
.
4) При перестановке двух строк (столбцов) матрицы ее определитель меняет свой знак на противоположный.
Пример:
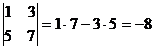 ;
; 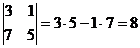 ;
; 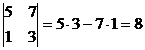 .
.
5) Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.
Пример:
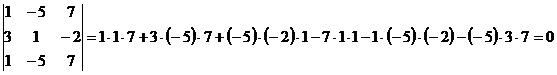 .
.
6) Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
Пример: Воспользуемся при вычислении свойствами 2) и 5) определителей:
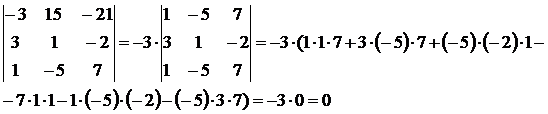
7) Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0, т.е.
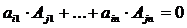 при i
при i  j.
j.
Пример: Посчитать: 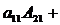
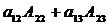 = 0 для данной матрицы
= 0 для данной матрицы
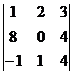 .
. 
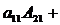
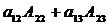 =
=
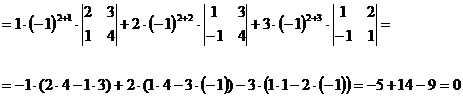 .
.
8) Определитель матрицы не изменяется, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.
Пример: Вычислить определитель матрицы С и матрицы С 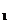 , полученной из матрицы С прибавлением ко второй строке матрицы С ее первой строки, умноженной на число -2:
, полученной из матрицы С прибавлением ко второй строке матрицы С ее первой строки, умноженной на число -2:
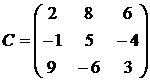
Воспользуемся уже полученным результатом определителя матрицы С:
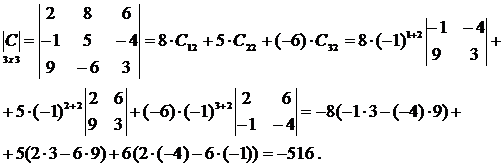
Преобразуем матрицу С согласно свойству: 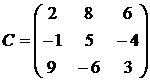
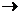
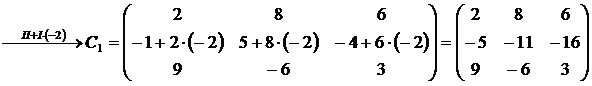 .
.
Теперь вычислим определитель получившейся матрицы:
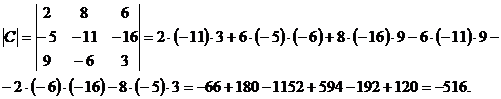
9) Сумма произведений произвольных чисел 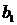 ,
, 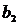 ,…,
,…, 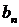 на алгебраические дополнения элементов любой строки (столбца) равны определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа
на алгебраические дополнения элементов любой строки (столбца) равны определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа 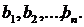
10) Определитель произведения двух квадратных матриц равен произведению их определителей:
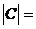
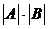 , где
, где 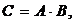 А и В – матрицы n-го порядка.
А и В – матрицы n-го порядка.
Пример: вычислить с помощью свойств определителя определитель матрицы В четвертого порядка
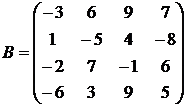 .
.
Решение:
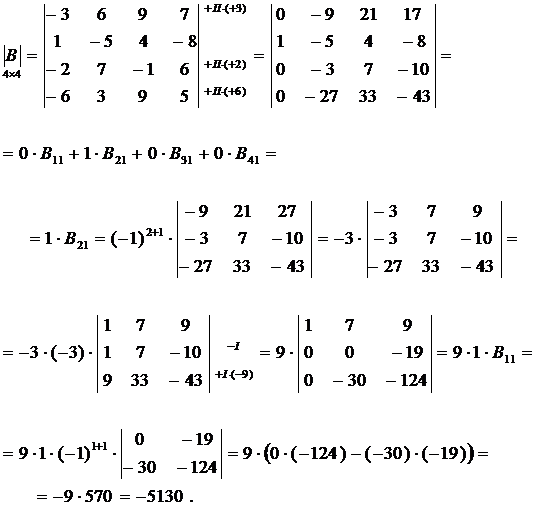
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1) Правило нахождения определителей второго порядка можно записать в виде формулы:
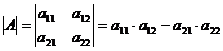
Вычислить определители 2-го порядка матриц:
а) 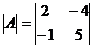 ; б)
; б) 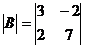 ; в)
; в) 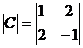 ; г)
; г) 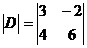 .
.
2) Для вычисления определителей третьего порядка используют правило Сарруса или правило треугольников, которое проще запоминается в виде следующих схем:

 (+)
(главная диагональ)
(+)
(главная диагональ)
|
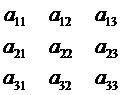
|  (-)
(другая диагональ)
(-)
(другая диагональ)
|
Вычислить определители 3-го порядка матриц по правилу Сарруса:
а) 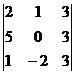 ; б)
; б) 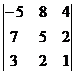 ; в)
; в) 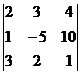 ;
;
3) Для вычисления определителей 4-го и более высокого порядка используют правило вычисления определителя методом разложения по элементам строки или столбца (по теореме Лапласа): определитель равен сумме произведений всех элементов какого-либо столбца (или строки) на соответствующие им алгебраические дополнения. Обычно вычисление проводится по элементам 1-й строки.
Можно использовать теорему Лапласа и для вычисления определителей 3-го порядка, когда разложение по первой строке имеет вид:
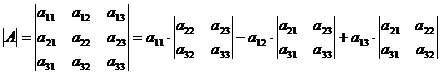
Вычислить определители 4-го и 3-го порядков:
а) 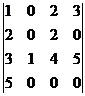 ; б)
; б) 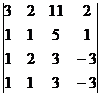 ; в)
; в) 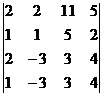 ;
;
г) 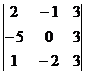 ; д)
; д) 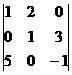 ; е)
; е) 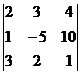 .
.
Замечание: Для сокращения вычислений удобно определитель раскладывать по элементам той строки или столбца, где содержится наибольшее количество нулей.
В этом случае нужно находить алгебраическое дополнения к элементам, равным 0; если же строки или столбцы не содержат достаточного количества нулей, то удобно провести эквивалентные преобразования. Используют правило: если ко всем элементам строки (столбца) прибавить соответствующие элементы другой строки (столбца); умноженные на одно и то же число; то определитель не изменяется.
III. «РАНГ МАТРИЦЫ»
Для решения и исследования некоторых математических и прикладных задач большое значение имеет понятие ранга матрицы.
Рассмотрим матрицу А размера 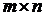 .
.
В матрице А размера 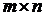 вычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы k- го порядка, где
вычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы k- го порядка, где 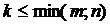 (меньшего из т и п). Определители таких подматриц называются минорами k- го порядка матрицы А. Один элемент матрицы называют минором первого порядка.
(меньшего из т и п). Определители таких подматриц называются минорами k- го порядка матрицы А. Один элемент матрицы называют минором первого порядка.
Из матрицы А размером 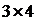 можно получить подматрицы 1-го, 2-го, 3-го порядков.
можно получить подматрицы 1-го, 2-го, 3-го порядков.
Пример: Выделим указанные подматрицы из данной матрицы 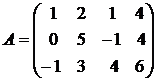 и запишем их миноры.
и запишем их миноры.
Решение:
Некоторые подматрицы первого порядка А  =
= 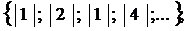
некоторые подматрицы второго порядка А  =
= 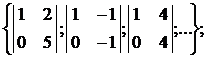
некоторые подматрицы третьего порядка А 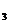 =
= 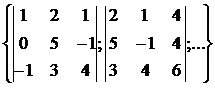 .
.
ОПРЕДЕЛЕНИЕ. Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы.
Обозначение: rang A или r(A)
Из определения следует:
1) 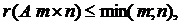 т.е., не превосходит меньшего из ее размеров;
т.е., не превосходит меньшего из ее размеров;
2) 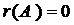 тогда и только тогда, когда все элементы матрицы равны нулю;
тогда и только тогда, когда все элементы матрицы равны нулю;
3) для квадратной матрицы п -го порядка 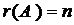 тогда и только тогда, когда матрица А – невырожденная, т.е., ее определитель не равен нулю.
тогда и только тогда, когда матрица А – невырожденная, т.е., ее определитель не равен нулю.
Пример: Вычислить 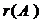 , если
, если
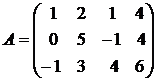 .
.
Решение: Начнем с перебора миноров третьего порядка.
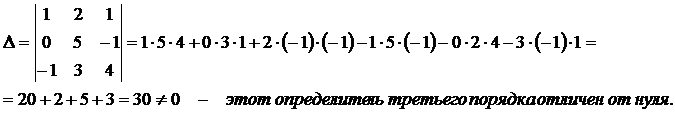 Таким образом, согласно определения ранга матрицы, можем сделать вывод, что ранг данной матрицы равен 3, т.е.,
Таким образом, согласно определения ранга матрицы, можем сделать вывод, что ранг данной матрицы равен 3, т.е., 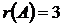 .
.
Замечание: В данном случае вычисление уже первого минора третьего порядка привело к искомому результату. В общем же случае определение ранга матрицы перебором миноров всех возможных порядков достаточно трудоемко.
Для упрощения решения этой задачи используются элементарные преобразования, сохраняющие ранг матрицы:
1) отбрасывание нулевой строки (столбца) матрицы;
2) умножение всех элементов строки (столбца) матрицы на число, не равное нулю;
3) изменение порядка строк (столбцов) матрицы;
4) прибавление к каждому элементу одной строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на одно и то же число;
5) транспонирование матрицы.
ТЕОРЕМА 1:Ранг матрицы не изменяется при элементарных преобразованиях матрицы.



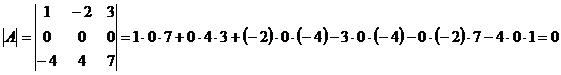 .
. , то и определитель матрицы умножится на это число
, то и определитель матрицы умножится на это число 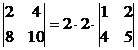 ;
;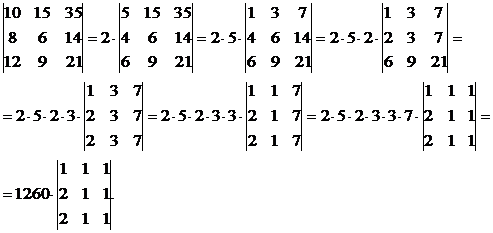
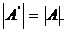
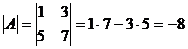 ;
; 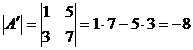 .
.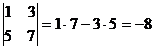 ;
; 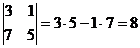 ;
; 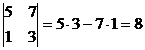 .
.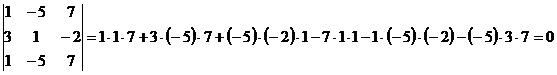 .
.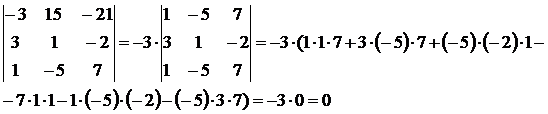
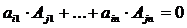 при i
при i  j.
j.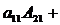
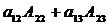 = 0 для данной матрицы
= 0 для данной матрицы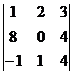 .
. 
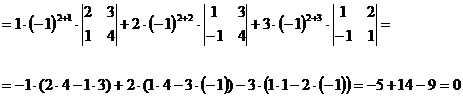 .
. , полученной из матрицы С прибавлением ко второй строке матрицы С ее первой строки, умноженной на число -2:
, полученной из матрицы С прибавлением ко второй строке матрицы С ее первой строки, умноженной на число -2: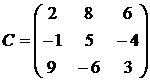
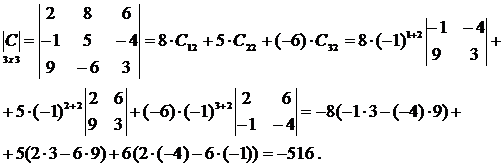
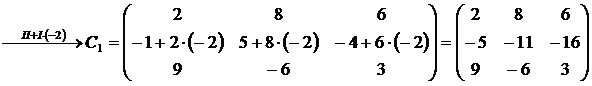 .
.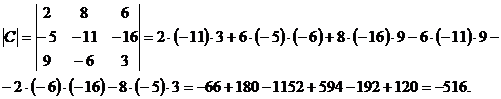
 ,
,  ,…,
,…, 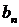 на алгебраические дополнения элементов любой строки (столбца) равны определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа
на алгебраические дополнения элементов любой строки (столбца) равны определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа 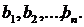
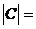
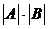 , где
, где 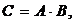 А и В – матрицы n-го порядка.
А и В – матрицы n-го порядка.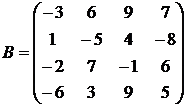 .
.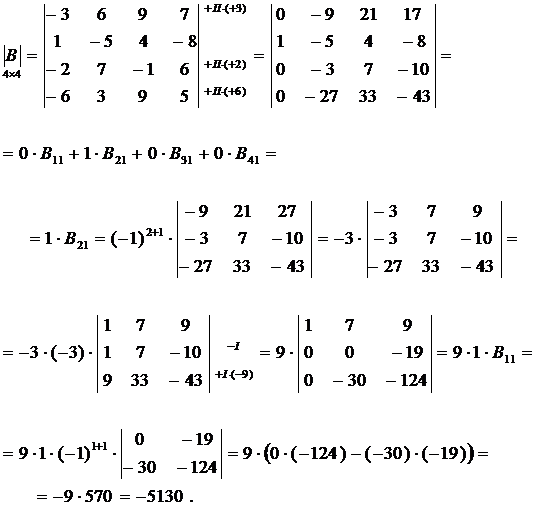
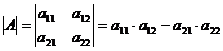
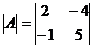 ; б)
; б) 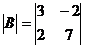 ; в)
; в) 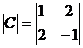 ; г)
; г) 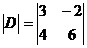 .
. (+)
(главная диагональ)
(+)
(главная диагональ)
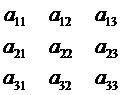
 (-)
(другая диагональ)
(-)
(другая диагональ)
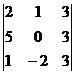 ; б)
; б) 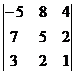 ; в)
; в) 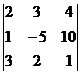 ;
;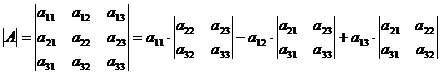
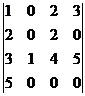 ; б)
; б) 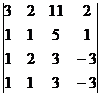 ; в)
; в) 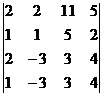 ;
;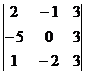 ; д)
; д) 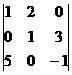 ; е)
; е)  .
. (меньшего из т и п). Определители таких подматриц называются минорами k- го порядка матрицы А. Один элемент матрицы называют минором первого порядка.
(меньшего из т и п). Определители таких подматриц называются минорами k- го порядка матрицы А. Один элемент матрицы называют минором первого порядка.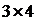 можно получить подматрицы 1-го, 2-го, 3-го порядков.
можно получить подматрицы 1-го, 2-го, 3-го порядков.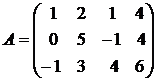 и запишем их миноры.
и запишем их миноры.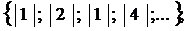
 =
= 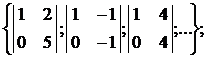
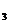 =
= 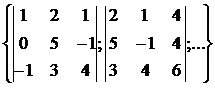 .
.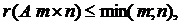 т.е., не превосходит меньшего из ее размеров;
т.е., не превосходит меньшего из ее размеров;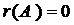 тогда и только тогда, когда все элементы матрицы равны нулю;
тогда и только тогда, когда все элементы матрицы равны нулю;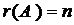 тогда и только тогда, когда матрица А – невырожденная, т.е., ее определитель не равен нулю.
тогда и только тогда, когда матрица А – невырожденная, т.е., ее определитель не равен нулю.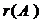 , если
, если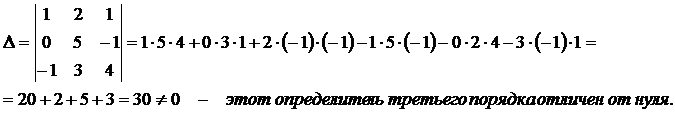 Таким образом, согласно определения ранга матрицы, можем сделать вывод, что ранг данной матрицы равен 3, т.е.,
Таким образом, согласно определения ранга матрицы, можем сделать вывод, что ранг данной матрицы равен 3, т.е., 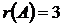 .
.


