Ряды.
§1. Числовые ряды.
- Основные понятия. Примеры.
Определение: Пусть { an } – числовая последовательность. Выражение a 1 +a 2 +…+a 3 +…= 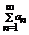 называется числовым рядом. Числа а 1, а 2, … - члены ряда, причем an – общий член ряда. Сумма Sn=a 1 +a 2 +…+a 3 =
называется числовым рядом. Числа а 1, а 2, … - члены ряда, причем an – общий член ряда. Сумма Sn=a 1 +a 2 +…+a 3 = 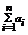 называется n-ой частичной суммой данного ряда (сумма первых n членов ряда).
называется n-ой частичной суммой данного ряда (сумма первых n членов ряда).
Определение: Если существует конечный предел последовательности { Sn } равный S, то ряд называется сходящимся, а число S – его суммой. 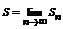 .
.
Если же такого предела не существует, либо он равен 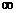 , то ряд называется расходящимся.
, то ряд называется расходящимся.
Предложение: Ряд 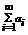 - сходится
- сходится 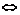 ,
, 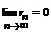 (последовательность остатков
(последовательность остатков 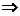 0).
0).
Доказательство. Из равенства 1 можно представить rn = S - Sn, тогда 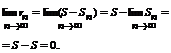
2. Простейшие свойства числовых рядов.
1.Перестановка, отбрасывание или добавление конечного числа членов ряда не влияет на его сходимость или расходимость.
2.Пусть ряд 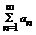 и ряд
и ряд 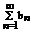 - сходится, тогда сумма этих рядов
- сходится, тогда сумма этих рядов 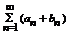 тоже сходится.
тоже сходится.
Доказательство. 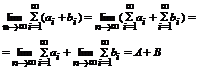 - предел существует.
- предел существует.
1.Если ряд 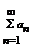 - сходится, то и ряд
- сходится, то и ряд 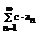 -сходится, где c - некоторое число. Что всякая линейная комбинация сходящихся рядов есть сходящийся ряд.
-сходится, где c - некоторое число. Что всякая линейная комбинация сходящихся рядов есть сходящийся ряд.
§2. Необходимые условия сходимости числового ряда. Гармонический ряд.
Теорема 1 (необходимый признак сходимости). Если ряд  - сходится, то общий член ряда → 0 (
- сходится, то общий член ряда → 0 (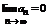 ).
).
Доказательство. Между частичными суммами существует следующая связь: Sn = Sn -1+ an, и поэтому 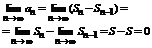 .
.
Следствие: (достаточный признак расходимости). Если 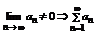 , то ряд расходится.
, то ряд расходится.
Пример1. 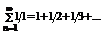 -гармонический ряд.
-гармонический ряд. 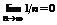 → ряд расходится.
→ ряд расходится.
§3. Признаки сходимости рядов с неотрицательными членами.
Общий вид:  ,
, 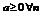 .
.
Теорема 1 (предельный признак сравнения). Пусть  и
и 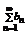 с положительными членами. Если существует
с положительными членами. Если существует  , который
, который 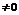 и
и 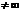 , тогда ряды
, тогда ряды  и
и 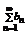 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Доказательство. Обозначим 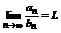 ;
; 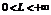 . Согласно определению обозначим все члены последовательности {
. Согласно определению обозначим все члены последовательности { 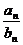 } начиная с некоторого номера находящегося сколь угодно близко к L, т.е.
} начиная с некоторого номера находящегося сколь угодно близко к L, т.е. 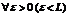 существует номер
существует номер 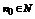 такой, что
такой, что 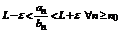 .
.
Умножим все части неравенства на bn (bn >0), получим следующее:
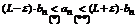 .
.
1.Пусть сходится ряд 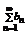 , тогда сходится
, тогда сходится 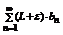 и тогда согласно теореме 3 ввиду неравенства (**) сходится ряд
и тогда согласно теореме 3 ввиду неравенства (**) сходится ряд  .
.
2.Пусть сходится ряд  , тогда согласно теореме 3 ввиду неравенства (**) сходится ряд
, тогда согласно теореме 3 ввиду неравенства (**) сходится ряд 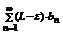 из чего следует сходимость
из чего следует сходимость 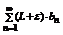 .
.
Аналогично доказывается случай расходимости.
Замечание. Применяя признак сходимости чаще всего сравнивают с 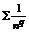 и
и 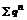 .
.
Теорема 2 (признак сравнения). Пусть имеется два ряда  и
и 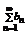 и существует номер n 0
и существует номер n 0 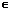 N такой, что выполняется следующее неравенство
N такой, что выполняется следующее неравенство 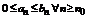 , тогда:
, тогда:
1. если ряд 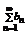 - сходится
- сходится 
 - сходится.
- сходится.
2. если ряд  - расходится
- расходится 
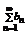 - расходится.
- расходится.
Доказательство. Можно считать, что члены второго ряда 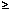 членам первого ряда уже начиная с первого номера (иначе можно рассматривать остатки ряда; их сходимость и расходимость равносильна сходимости или расходимости рядов). Считаем, что неравенства
членам первого ряда уже начиная с первого номера (иначе можно рассматривать остатки ряда; их сходимость и расходимость равносильна сходимости или расходимости рядов). Считаем, что неравенства 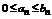 выполняется для
выполняется для 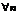 , тогда аналогичное неравенство выполняется и для { Sn }, т.е.
, тогда аналогичное неравенство выполняется и для { Sn }, т.е. 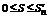 .
.
1. Пусть 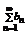 - сходится, тогда последовательность {
- сходится, тогда последовательность { 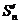 }- ограничена, значит ограничена и последовательность { Sn }
}- ограничена, значит ограничена и последовательность { Sn } 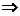
 - сходится.
- сходится.
2. Пусть  - расходится. Это означает, что неограниченна его последовательность частичных сумм Sn = {
- расходится. Это означает, что неограниченна его последовательность частичных сумм Sn = { 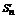 } – неограниченна, значит расходится
} – неограниченна, значит расходится 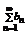 .
.
§4.Признаки Д’ Аламбера и Коши сходимости знакоположительных числовых рядов.
Теорема 1 (признак Д’Аламбера). Пусть  ,
, 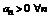 и пусть существует
и пусть существует 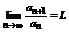 , тогда:
, тогда:
1. Если L <1 - сходится.
2. Если L >1 - расходится.
Доказательство. Согласно определению интеграла для 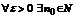 такой, что
такой, что 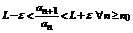 .
.
1.Пусть L <1, тогда можно выбрать 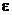 такое, что
такое, что 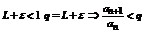 , так как an >0 an +1< qan
, так как an >0 an +1< qan 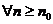 в частности
в частности 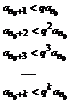 .
.
Рассмотрим ряд, членами которого являются правые части 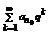 - геометрическая прогрессия со знаменателем
- геометрическая прогрессия со знаменателем 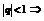 сходится, значит согласно теореме 3 сходится ряд
сходится, значит согласно теореме 3 сходится ряд
и из левых частей 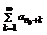 (но этот ряд равен исходному) =
(но этот ряд равен исходному) = 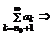 что сходится
что сходится 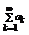 .
.
2. Пусть L >1 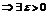 , такой, что
, такой, что 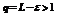 согласно левой части неравенства получаем, что
согласно левой части неравенства получаем, что 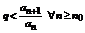 .
.
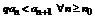
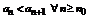 , т.к. q >1.
, т.к. q >1.
Это означает, что последовательность { an } – не убывающая по крайней мере начиная с номера n 0 тем самым 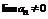 тогда не выполняется необходимый признак сходимости и значит ряд расходится.
тогда не выполняется необходимый признак сходимости и значит ряд расходится.
Теорема 2 (признак Коши). Пусть  ,
, 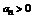 и пусть предел
и пусть предел 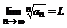 тогда:
тогда:
1. Если L <1 - сходится.
2. Если L >1 - расходится.
Доказательство. Согласно определению предела для 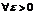 существует
существует 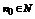 такой, что
такой, что 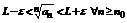 .
.
1. Пусть L <1; 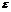 можно подобрать так, чтобы
можно подобрать так, чтобы 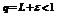
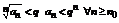
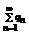 - сходится (прогрессия с
- сходится (прогрессия с 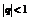 ), то
), то  - сходится по теореме 3.
- сходится по теореме 3.
2. Пусть L >1; 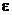 можно подобрать так, чтобы
можно подобрать так, чтобы 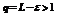
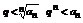
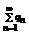 - расходится, тогда согласно теореме 3
- расходится, тогда согласно теореме 3  - расходится.
- расходится.
§5. Интегральный признак сравнения.
Теорема 2 (интегральный признак сходимости). Пусть  - ряд с положительными членами и существует функция f (x) > 0 непрерывная и определенная на интервале [1; +
- ряд с положительными членами и существует функция f (x) > 0 непрерывная и определенная на интервале [1; + 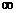 ),
),
такая что f (n)= an, 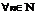 . Ряд
. Ряд  сходится
сходится 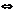 , когда сходится
, когда сходится 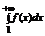 .
.
 - ряд Дирихле: при p >1 – ряд сходится;
- ряд Дирихле: при p >1 – ряд сходится;
при p 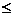 1 – ряд расходится.
1 – ряд расходится.
Доказательство. Для произвольного действительного числа x найдутся целые числа k такие, что 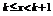 . Так как f (x) монотонно убывает:
. Так как f (x) монотонно убывает: 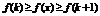 . Перейдем к интегралам в неравенстве:
. Перейдем к интегралам в неравенстве: 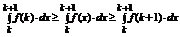
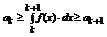 .
.
Просуммируем эти неравенства при всех k =1,.., n.
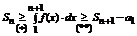 .
.
b) Пусть сходится  , где I – число, тогда
, где I – число, тогда 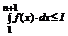 . Это означает по неравенству (**), что Sn +1- a 1
. Это означает по неравенству (**), что Sn +1- a 1 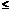 I, т.е.
I, т.е. 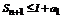 последовательность частичных сумм ограничена.
последовательность частичных сумм ограничена.
c) Пусть  - сходится, тогда { Sn } – ограничена. Согласно неравенству (*), тогда и последовательность интегралов {
- сходится, тогда { Sn } – ограничена. Согласно неравенству (*), тогда и последовательность интегралов { 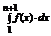 } – ограничена и значит она сходится при
} – ограничена и значит она сходится при 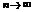 , т.е. сходится несобственный интеграл
, т.е. сходится несобственный интеграл 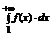 - сходится.
- сходится.
Пусть ряд  - расходится, т.е. расходится последовательность { Sn } – (неограниченно возрастает). Тогда Sn +1- a 1 – также неограниченно возрастает. В силу неравенства (**) последовательность {
- расходится, т.е. расходится последовательность { Sn } – (неограниченно возрастает). Тогда Sn +1- a 1 – также неограниченно возрастает. В силу неравенства (**) последовательность { 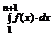 }–
}–
d) неограниченно возрастает. Тогда 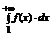 - расходится.
- расходится.
e) Если расходится интеграл 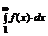
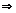 по (*) что
по (*) что  - расходится.
- расходится.
q <1 – сход.
q >1- расход.
§6,7. Знакопеременные ряды. Знакочередующиеся ряды. Признак Лейбница.
6. Знакопеременные ряды. Абсолютная и условная сходимость.
Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные.
Теорема1. Если знакопеременный ряд 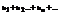 таков, что ряд, составленный из абсолютных величин его членов
таков, что ряд, составленный из абсолютных величин его членов 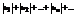 сходится, то и данный знакопеременный ряд также сходится.
сходится, то и данный знакопеременный ряд также сходится.
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов. Если же знакопеременный ряд сходится, а ряд, составленный из абсолютных величин его членов расходится, то данный ряд называется условно или не абсолютно сходящимся рядом.
Знакопеременными называются ряды, которые содержат как положительные, так и отрицательные члены, со сколь угодно большими номерами.
Частным случаем таких рядов являются знакочередующие, т.е. ряды, в которых любые 2 соседних члена имеют разные знаки.
Знакочередующие ряды удобно представить в виде 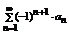 (*), где
(*), где 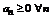 (в случае если a 1>0).
(в случае если a 1>0).
Теорема 1 (признак Лейбница). Пусть знакочередующийся ряд (*) удовлетворяет следующим условиям:
1. 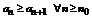 (начиная с номера n0 монотонно убывает).
(начиная с номера n0 монотонно убывает).
2. 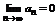 ,
,
тогда данный ряд сходится, причем для 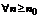 справедливо следующая оценка остатка
справедливо следующая оценка остатка 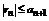 .
.
Доказательство. Можно считать, что условие 1 выполняется для всех n. Рассмотрим частичную сумму S 2 n. Сгруппируем слагаемые следующим образом:
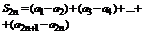
каждая разность в скобках неотрицательная. Т.е. последовательность 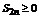 и S 2 n возрастающая последовательность.
и S 2 n возрастающая последовательность.
С другой стороны последовательность S 2 n представима следующим образом 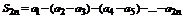 , опять в скобках все разности неотрицательны
, опять в скобках все разности неотрицательны 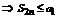 .
.
Тем самым последовательность { S 2 n } ограничена и значит она сходится.
Обозначим через 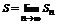 .
.
Рассмотрим 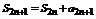 , тогда
, тогда 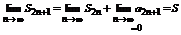 .
.
Таким образом все частичные суммы имеют предел S. Из полученных оценок 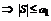 , поэтому n -ый частичный остаток
, поэтому n -ый частичный остаток 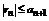 .
.
Пример. 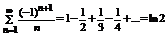 .
.
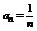 - убывающая последовательность
- убывающая последовательность 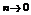 , значит условие признака Лейбница выполняется - ряд сходится.
, значит условие признака Лейбница выполняется - ряд сходится.
§8. Признаки условной сходимости. Особенности условно сходящихся рядов.
Теорема Дирихле (признак Дирихле). Если частичная сумма an ряда 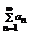 образует ограниченную последовательность, кроме того последовательность { bn } монотонно убывает и
образует ограниченную последовательность, кроме того последовательность { bn } монотонно убывает и 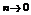 , то ряд
, то ряд 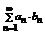 - сходится.
- сходится.
Признак Лейбница является частным случаем данной теоремы.
Теорема Абеля. Пусть ряд 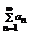 - сходится и { bn } монотонно убывающая последовательность состоящая из положительных членов. Тогда ряд
- сходится и { bn } монотонно убывающая последовательность состоящая из положительных членов. Тогда ряд 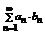 - сходится.
- сходится.
Теорема Римана. Пусть ряд 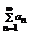 -сходится условно и его сумма:
-сходится условно и его сумма: 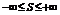 , тогда существует такая перестановка членов данного ряда после которой исходный ряд сходится и его сумма = S.
, тогда существует такая перестановка членов данного ряда после которой исходный ряд сходится и его сумма = S.
§9. Функциональные ряды.
Пусть u 1(x), u 2(x)…- последовательность функций, определенных на множестве X. 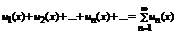 - называется функциональным рядом.
- называется функциональным рядом.
Для всякого числа 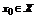 ряд
ряд 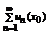 - обычный числовой ряд.
- обычный числовой ряд.
Если данный числовой ряд сходится, то x 0 – точка сходимости данного функционального ряда. Множество всех точек сходимости называется областью сходимости функционального ряда (D). 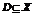 .
.
Функция 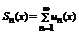 называется n-ой частичной суммой данного ряда, а функция
называется n-ой частичной суммой данного ряда, а функция 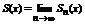 называется суммой данного ряда. Функция
называется суммой данного ряда. Функция 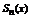 определена на множестве D.
определена на множестве D.
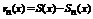 - n-ый частичный остаток данного ряда. Переходя к пределу видим, что
- n-ый частичный остаток данного ряда. Переходя к пределу видим, что 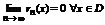 .
.
Сходимость о которой идет речь выше называется поточечной сходимостью.
Если сходящийся ряд  в какой-то точке xn, то такая сходимость называется абсолютной.
в какой-то точке xn, то такая сходимость называется абсолютной.
Множество D 1 точек x 0 в которых ряд сходится абсолютно называется областью абсолютной сходимости ряда 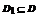 .
.
2. Равномерная сходимость функциональных рядов.
Функциональный ряд 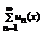 называется равномерно сходящимся в области D к
называется равномерно сходящимся в области D к 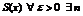 (не зависящее от x),
(не зависящее от x), 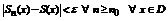
Дадим параллельную формулировку поточечной сходимости.
Ряд 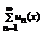 называется поточечно сходящимся к сумме
называется поточечно сходящимся к сумме 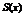 в области D, если
в области D, если 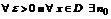 (вообще говоря зависящее от x), такой что
(вообще говоря зависящее от x), такой что 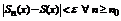 .
.
3. Признак Вейерштрасса.
Теорема. Если для функционального ряда 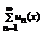
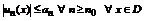 , причем ряд
, причем ряд 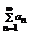 - сходится. Тогда функциональный ряд
- сходится. Тогда функциональный ряд 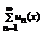 сходится равномерно на множестве D.
сходится равномерно на множестве D.
Доказательство. Обозначим через 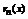 n -ый частичный остаток
n -ый частичный остаток 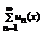 , а через
, а через 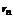 n-ый частичный остаток
n-ый частичный остаток 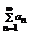 . Так как ряд
. Так как ряд 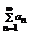 - сходится
- сходится 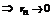 , т.е.
, т.е. 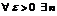 (не зависящее от x) такой что
(не зависящее от x) такой что 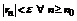 .
.
В силу условия теоремы 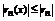 ;
; 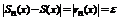
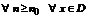 . Ряд сходится равномерно на D.
. Ряд сходится равномерно на D.
Числовой ряд 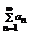 в формулировке теоремы называется мажоритарным рядом для данного функционального мажорантой. Функциональный ряд для которого существует мажоранта называется мажорируемым.
в формулировке теоремы называется мажоритарным рядом для данного функционального мажорантой. Функциональный ряд для которого существует мажоранта называется мажорируемым.
Достаточным признаком равномерной сходимости функционального ряда являются мажоранты, которые сходятся.
Данный признак достаточный, но не необходимый. Это значит, что если мажоранты не существуют, то нельзя говорить о том, что ряд сходится.
4. Свойства равномерно сходящихся рядов.
Теорема 1 (о непрерывности суммы равномерно сходящихся рядов). Если на множестве D функциональный ряд 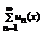 с непрерывными членами сходится равномерно, то его сумма S (x) непрерывна на этом множестве.
с непрерывными членами сходится равномерно, то его сумма S (x) непрерывна на этом множестве.
Доказательство. Согласно определению равномерной сходимости для 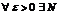 (не зависящий от x) такой что
(не зависящий от x) такой что 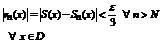 . Пусть
. Пусть  , для
, для  условие выполняется.
условие выполняется.
Функция 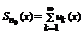 непрерывна на множестве D. Как конечная сумма непрерывных функций. Для любого
непрерывна на множестве D. Как конечная сумма непрерывных функций. Для любого 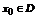 и для выбранного
и для выбранного 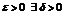 такое что
такое что 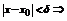
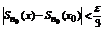 (определение непрерывности
(определение непрерывности 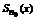 ).
).
Тогда для выбранного 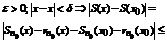
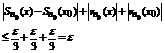 .
.
Теорема 2 (о почленном интегрировании равномерно сходящихся рядов).
Если функциональный ряд 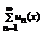 сходится к функции S (x) равномерно на отрезке
сходится к функции S (x) равномерно на отрезке 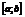 , то его можно почленно интегрировать по любому отрезку
, то его можно почленно интегрировать по любому отрезку 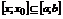 и справедливо равенству
и справедливо равенству 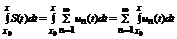 , причем последний ряд сходится равномерно на отрезке
, причем последний ряд сходится равномерно на отрезке 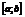 .
.
Доказательство. В силу равномерной сходимости данного функционального ряда для 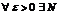 (не зависит от x), такой что
(не зависит от x), такой что  .
.
Тогда 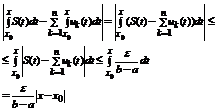
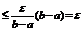 . Справедливо
. Справедливо 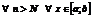 . А это означает, что ряд
. А это означает, что ряд 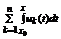 - сходится равномерно на
- сходится равномерно на 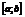 к
к  .
.
Теорема 3 (о почленном дифференцировании равномерно сходящихся рядов). Если ряд 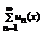 сходится на отрезке
сходится на отрезке 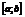 к сумме S (x).Члены ряда
к сумме S (x).Члены ряда 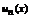 дифференцированы на отрезке и ряд сумма
дифференцированы на отрезке и ряд сумма 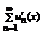 - сходится на
- сходится на 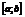 - равномерно, то данный ряд так же сходится на
- равномерно, то данный ряд так же сходится на 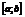 равномерно, причем его сумма дифференцирована на
равномерно, причем его сумма дифференцирована на 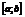 и выполняется равенство
и выполняется равенство 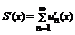 . (*)
. (*)
§10. Степенные ряды.
Функциональный ряд вида 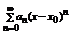 , где
, где 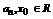 называется степенным рядом по степеням
называется степенным рядом по степеням 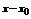 .
.
С помощью замены 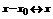 получим ряд
получим ряд 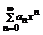 . Исходный получается обратной заменой из данного.
. Исходный получается обратной заменой из данного.
Теорема Абеля (о сходимости степенных рядов). Для всякого степенного ряда 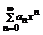 существует неотрицательное число R (возможно
существует неотрицательное число R (возможно 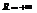 ) такое, что ряд сходится абсолютно при
) такое, что ряд сходится абсолютно при 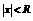 - сходится равномерно при
- сходится равномерно при 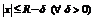 - расходится при
- расходится при 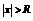 .
.
Доказательство. Ряд заведомо сходится при x =0. Если других точек сходимости нету, то очевидно число R =0.
Предположим, что 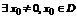 (область сходимости). Так как ряд
(область сходимости). Так как ряд 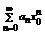 - сходится, то согласно признаку сходимости общий член ряда
- сходится, то согласно признаку сходимости общий член ряда 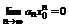 . Это означает, что последовательность
. Это означает, что последовательность 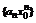 , будучи сходящейся, ограничена, т.е.
, будучи сходящейся, ограничена, т.е. 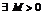 , так что
, так что 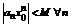
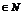 пусть x такой, что
пусть x такой, что 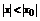 .
. 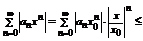 (в силу оценок полученных выше)
(в силу оценок полученных выше) 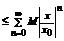 - сходится как сумма геометрической прогрессии (
- сходится как сумма геометрической прогрессии (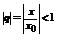 ).
).
Получаем, что данный степенной ряд сходится абсолютно при любом x, таком, что 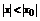 .
.
Отсюда видно, что в качестве R можно взять 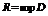 (D - область сходимости).
(D - область сходимости).
При 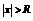 - ряд расходится, поскольку мы оказываемся за пределами границы области сходимости.
- ряд расходится, поскольку мы оказываемся за пределами границы области сходимости.
Если 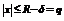 , то
, то 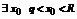 . Тогда получаем, что
. Тогда получаем, что 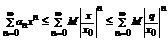 - мажоритарный ряд для
- мажоритарный ряд для 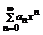 , который сходится, так как это геометрическая прогрессия (
, который сходится, так как это геометрическая прогрессия (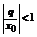 ). Значит данный ряд сходится равномерно в указанной области согласно признаку Вейерштрасса.
). Значит данный ряд сходится равномерно в указанной области согласно признаку Вейерштрасса.
Замечание. Число R, о котором идет речь в условии теоремы, называется радиусом сходимости данного функционального ряда. Интервал (- R; R), внутри которого ряд сходится абсолютно называется интегралом сходимости.
Степенной ряд по степеням (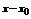 ) то он имеет интервал сходимости (
) то он имеет интервал сходимости (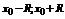 ).
).
Кроме интервала сходимости в область сходимости могут входить края.
2. Свойства степенных рядов.
1. Сумма степенного ряда непрерывна на интервале сходимости (причем 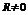 ).
).
Доказательство. Пусть 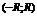 - интервал сходимости:
- интервал сходимости: 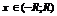 .
. 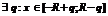 . По теореме Абеля ряд сходится равномерно на
. По теореме Абеля ряд сходится равномерно на 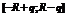 и, значит, сумма его непрерывна во всех точках данного отрезка, в частности, в точке x.
и, значит, сумма его непрерывна во всех точках данного отрезка, в частности, в точке x.
2. Операция почленного дифференцирования и интегрирования по любому отрезку от 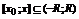 степенного ряда не имеет его радиуса сходимости.
степенного ряда не имеет его радиуса сходимости.
Доказательство. Предположим, что существует предел 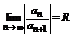 . Рассмотрим ряд полученный почленным дифференцированием ряда
. Рассмотрим ряд полученный почленным дифференцированием ряда 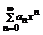 , получим
, получим 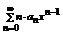 .
.
Пусть радиус сходимости 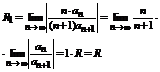 .
.
Рассмотрим ряд полученный почленным интегрированием x 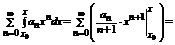
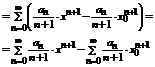 .
.
Второй ряд из этих двух является числовым и он сходится, поскольку 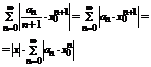 сходится, т.к.
сходится, т.к. 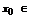 интервалу сходимости.
интервалу сходимости.
Вычислим 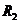 (радиус сходимости первого ряда).
(радиус сходимости первого ряда). 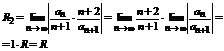 .
.
3. Степенной ряд можно любое количество раз дифференцировать на отрезке сходимости 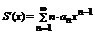 .
.
Доказательство. Вытекает из теоремы о почленном дифференцирование функциональных рядов.
4. Степенной ряд можно почленно интегрировать любое количество раз по любому отрезку  .
.
§11. Ряды Тейлора.
Пусть функция 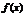 - бесконечно дифференцирован в окрестности точки
- бесконечно дифференцирован в окрестности точки 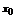 (т.е существует производная). Поставим этой функции в соответствие ряд
(т.е существует производная). Поставим этой функции в соответствие ряд 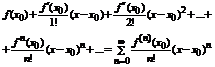 . Данный ряд называется рядом Тейлора функции
. Данный ряд называется рядом Тейлора функции 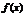 в окрестности точки
в окрестности точки 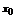 . В частном случае, когда
. В частном случае, когда 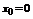 , получаем
, получаем 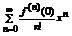 - ряд Маклорена функции
- ряд Маклорена функции 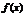 .
.
Замечание 1. Ряд Тейлора является степенным рядом, следовательно имеет радиус сходимости и интервал сходимости. Однако сумма ряда необязательно совпадает с функцией 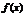 . За пределами интервала сходимости сумма проста не существует.
. За пределами интервала сходимости сумма проста не существует.
Если же сумма ряда 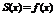 на
на 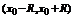 то говорят, что функция
то говорят, что функция 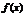 разложима в ряд Тейлора в окрестности точки
разложима в ряд Тейлора в окрестности точки 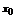 .
.
Замечание 2. Частичные суммы ряда Тейлора представляются следующими многочленами: 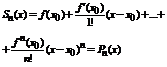 , которые есть ничто иное, как многочлены Тейлора (обозначим их через P (x)).
, которые есть ничто иное, как многочлены Тейлора (обозначим их через P (x)).
Существует формула Тейлора, которая имеет вид: 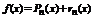 , где
, где 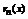 - остаток формулы Тейлора. Для остатка были получены следующие оценки:
- остаток формулы Тейлора. Для остатка были получены следующие оценки: 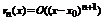 - оценка остатка в форме Пеана, а также
- оценка остатка в форме Пеана, а также 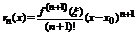 , где точка
, где точка 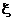 расположена между x 0 и x. Оценка остатка формулы Тейлора в форме Лагранжа.
расположена между x 0 и x. Оценка остатка формулы Тейлора в форме Лагранжа.
Обозначим через 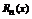 - остаток ряда Тейлора. Вообще говоря
- остаток ряда Тейлора. Вообще говоря 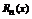 и
и 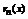 не одно и тоже. Действительно
не одно и тоже. Действительно 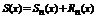 и формула Тейлора
и формула Тейлора 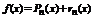 одно и тоже.
одно и тоже.
Но если 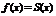 , т.е. функция
, т.е. функция 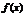 - разложима в ряд Тейлора, то остаток ряда Тейлора совпадает с остатком формулы Тейлора.
- разложима в ряд Тейлора, то остаток ряда Тейлора совпадает с остатком формулы Тейлора.
Это позволяет для оценки остатка ряда Тейлора использовать оценки остатка формулы Тейлора.
Теорема 1. Для того, чтобы бесконечно дифференцированная функция 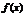 разложилась в ряд Тейлора в окрестности точки
разложилась в ряд Тейлора в окрестности точки 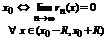 .
.
Доказательство. Мы уже отметили, что разложение означает 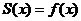 , а это в свою очередь
, а это в свою очередь 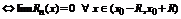 .
.
Теорема 2 (достаточный признак разложения в ряд Тейлора). Если 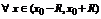 , все производные функции
, все производные функции 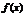 ограничены одной и той же константой M (это свойство называется равномерной ограниченностью на данном интервале), то ряд Тейлора функции
ограничены одной и той же константой M (это свойство называется равномерной ограниченностью на данном интервале), то ряд Тейлора функции 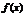 - сходится к функции
- сходится к функции 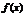 .
.
Доказательство. Воспользовавшись теоремой 1 покажем, что 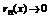 . Применим формулу Лагранжа, для оценки остатка формулы Тейлора. Имеем:
. Применим формулу Лагранжа, для оценки остатка формулы Тейлора. Имеем:
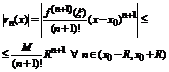 .
.
Числовой ряд 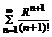 - сходится по признаку Д’Аламбера, то согласно необходимому признаку сходимости. Предел
- сходится по признаку Д’Аламбера, то согласно необходимому признаку сходимости. Предел 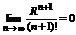 .
.
Таким образом и 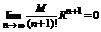 . Следовательно ввиду оценки и
. Следовательно ввиду оценки и 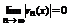 .
.
Теорема 3 Если степенной ряд по степеням 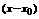 - сходится к функции
- сходится к функции 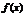 в окрестности точки
в окрестности точки 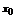 , то он является рядом Тейлора для данной функции.
, то он является рядом Тейлора для данной функции.
Доказательство. Пусть 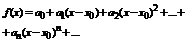 Согласно свойствам степенной ряд можно любое количество раз почленно дифференцировать в окрестности точки
Согласно свойствам степенной ряд можно любое количество раз почленно дифференцировать в окрестности точки 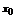 .
.
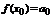 .
.
После дифференцирования: 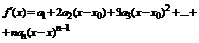
Из полученных равенств находим, что 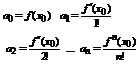 .
.
Т.е. коэффициенты совпадают с коэффициентом ряда Тейлора.
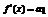
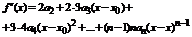
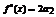 ……………
……………
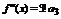
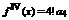 ………………
………………
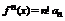 .
.
§12. Разложение функций в ряд Тейлора (Маклорена).
1) 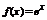 .
.
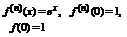 .
.
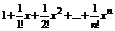 (*)
(*)
Покажем, что ряд сходится к e.

Полученный ряд (*) сходится к функции 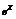 для любого x.
для любого x.
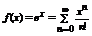 - расходится на R.
- расходится на R.
2)
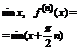
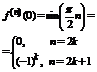
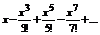
3)
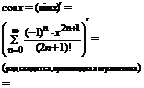
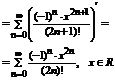 .
.
4) 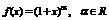
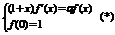 - дифференциальное уравнение, с начальным условием.
- дифференциальное уравнение, с начальным условием.
Задача Коши.
5) 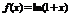
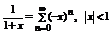
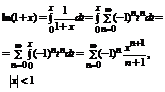 .
.
Сходится на 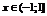 .
.
15. Приложения степенных рядов. Приближенное вычисление значений ф-ций. Вычисление сумм числовых рядов.
Приближенное в


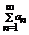 называется числовым рядом. Числа а 1, а 2, … - члены ряда, причем an – общий член ряда. Сумма Sn=a 1 +a 2 +…+a 3 =
называется числовым рядом. Числа а 1, а 2, … - члены ряда, причем an – общий член ряда. Сумма Sn=a 1 +a 2 +…+a 3 = 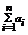 называется n-ой частичной суммой данного ряда (сумма первых n членов ряда).
называется n-ой частичной суммой данного ряда (сумма первых n членов ряда).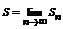 .
.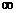 , то ряд называется расходящимся.
, то ряд называется расходящимся.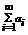 - сходится
- сходится 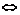 ,
, 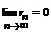 (последовательность остатков
(последовательность остатков 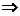 0).
0).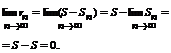
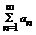 и ряд
и ряд 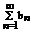 - сходится, тогда сумма этих рядов
- сходится, тогда сумма этих рядов 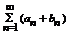 тоже сходится.
тоже сходится.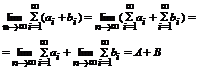 - предел существует.
- предел существует.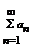 - сходится, то и ряд
- сходится, то и ряд 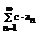 -сходится, где c - некоторое число. Что всякая линейная комбинация сходящихся рядов есть сходящийся ряд.
-сходится, где c - некоторое число. Что всякая линейная комбинация сходящихся рядов есть сходящийся ряд. - сходится, то общий член ряда → 0 (
- сходится, то общий член ряда → 0 (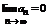 ).
).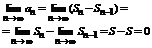 .
.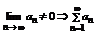 , то ряд расходится.
, то ряд расходится.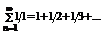 -гармонический ряд.
-гармонический ряд. 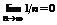 → ряд расходится.
→ ряд расходится.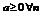 .
.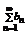 с положительными членами. Если существует
с положительными членами. Если существует  , который
, который 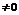 и
и 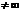 , тогда ряды
, тогда ряды 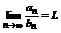 ;
; 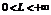 . Согласно определению обозначим все члены последовательности {
. Согласно определению обозначим все члены последовательности { 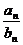 } начиная с некоторого номера находящегося сколь угодно близко к L, т.е.
} начиная с некоторого номера находящегося сколь угодно близко к L, т.е. 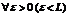 существует номер
существует номер 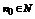 такой, что
такой, что 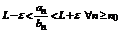 .
.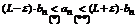 .
.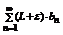 и тогда согласно теореме 3 ввиду неравенства (**) сходится ряд
и тогда согласно теореме 3 ввиду неравенства (**) сходится ряд 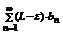 из чего следует сходимость
из чего следует сходимость 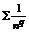 и
и 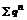 .
.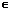 N такой, что выполняется следующее неравенство
N такой, что выполняется следующее неравенство 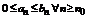 , тогда:
, тогда: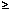 членам первого ряда уже начиная с первого номера (иначе можно рассматривать остатки ряда; их сходимость и расходимость равносильна сходимости или расходимости рядов). Считаем, что неравенства
членам первого ряда уже начиная с первого номера (иначе можно рассматривать остатки ряда; их сходимость и расходимость равносильна сходимости или расходимости рядов). Считаем, что неравенства 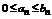 выполняется для
выполняется для 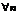 , тогда аналогичное неравенство выполняется и для { Sn }, т.е.
, тогда аналогичное неравенство выполняется и для { Sn }, т.е. 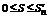 .
.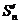 }- ограничена, значит ограничена и последовательность { Sn }
}- ограничена, значит ограничена и последовательность { Sn } 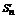 } – неограниченна, значит расходится
} – неограниченна, значит расходится 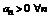 и пусть существует
и пусть существует 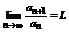 , тогда:
, тогда: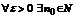 такой, что
такой, что 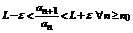 .
.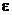 такое, что
такое, что 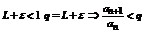 , так как an >0 an +1< qan
, так как an >0 an +1< qan 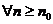 в частности
в частности 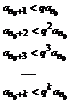 .
.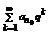 - геометрическая прогрессия со знаменателем
- геометрическая прогрессия со знаменателем 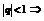 сходится, значит согласно теореме 3 сходится ряд
сходится, значит согласно теореме 3 сходится ряд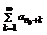 (но этот ряд равен исходному) =
(но этот ряд равен исходному) = 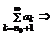 что сходится
что сходится 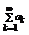 .
.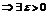 , такой, что
, такой, что 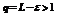 согласно левой части неравенства получаем, что
согласно левой части неравенства получаем, что 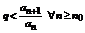 .
.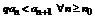
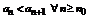 , т.к. q >1.
, т.к. q >1.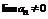 тогда не выполняется необходимый признак сходимости и значит ряд расходится.
тогда не выполняется необходимый признак сходимости и значит ряд расходится.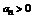 и пусть предел
и пусть предел 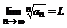 тогда:
тогда: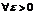 существует
существует 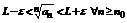 .
.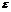 можно подобрать так, чтобы
можно подобрать так, чтобы 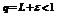
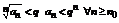
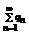 - сходится (прогрессия с
- сходится (прогрессия с 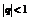 ), то
), то 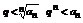
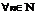 . Ряд
. Ряд 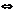 , когда сходится
, когда сходится 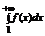 .
. - ряд Дирихле: при p >1 – ряд сходится;
- ряд Дирихле: при p >1 – ряд сходится;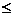 1 – ряд расходится.
1 – ряд расходится.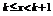 . Так как f (x) монотонно убывает:
. Так как f (x) монотонно убывает: 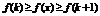 . Перейдем к интегралам в неравенстве:
. Перейдем к интегралам в неравенстве: 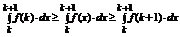
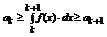 .
.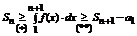 .
. , где I – число, тогда
, где I – число, тогда 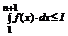 . Это означает по неравенству (**), что Sn +1- a 1
. Это означает по неравенству (**), что Sn +1- a 1 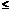 I, т.е.
I, т.е. 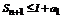 последовательность частичных сумм ограничена.
последовательность частичных сумм ограничена.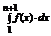 } – ограничена и значит она сходится при
} – ограничена и значит она сходится при 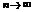 , т.е. сходится несобственный интеграл
, т.е. сходится несобственный интеграл 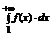 - сходится.
- сходится. }–
}–
 по (*) что
по (*) что 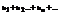 таков, что ряд, составленный из абсолютных величин его членов
таков, что ряд, составленный из абсолютных величин его членов 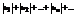 сходится, то и данный знакопеременный ряд также сходится.
сходится, то и данный знакопеременный ряд также сходится.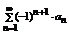 (*), где
(*), где 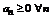 (в случае если a 1>0).
(в случае если a 1>0).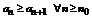 (начиная с номера n0 монотонно убывает).
(начиная с номера n0 монотонно убывает).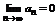 ,
,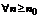 справедливо следующая оценка остатка
справедливо следующая оценка остатка 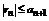 .
.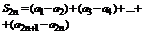
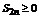 и S 2 n возрастающая последовательность.
и S 2 n возрастающая последовательность.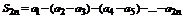 , опять в скобках все разности неотрицательны
, опять в скобках все разности неотрицательны 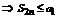 .
.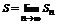 .
.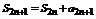 , тогда
, тогда 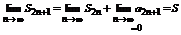 .
.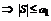 , поэтому n -ый частичный остаток
, поэтому n -ый частичный остаток 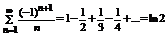 .
.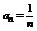 - убывающая последовательность
- убывающая последовательность 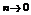 , значит условие признака Лейбница выполняется - ряд сходится.
, значит условие признака Лейбница выполняется - ряд сходится.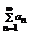 образует ограниченную последовательность, кроме того последовательность { bn } монотонно убывает и
образует ограниченную последовательность, кроме того последовательность { bn } монотонно убывает и 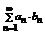 - сходится.
- сходится.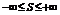 , тогда существует такая перестановка членов данного ряда после которой исходный ряд сходится и его сумма = S.
, тогда существует такая перестановка членов данного ряда после которой исходный ряд сходится и его сумма = S.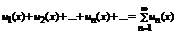 - называется функциональным рядом.
- называется функциональным рядом.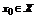 ряд
ряд 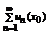 - обычный числовой ряд.
- обычный числовой ряд.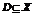 .
.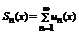 называется n-ой частичной суммой данного ряда, а функция
называется n-ой частичной суммой данного ряда, а функция 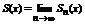 называется суммой данного ряда. Функция
называется суммой данного ряда. Функция 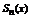 определена на множестве D.
определена на множестве D.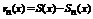 - n-ый частичный остаток данного ряда. Переходя к пределу видим, что
- n-ый частичный остаток данного ряда. Переходя к пределу видим, что 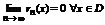 .
. в какой-то точке xn, то такая сходимость называется абсолютной.
в какой-то точке xn, то такая сходимость называется абсолютной.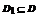 .
.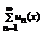 называется равномерно сходящимся в области D к
называется равномерно сходящимся в области D к 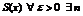 (не зависящее от x),
(не зависящее от x), 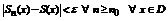
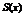 в области D, если
в области D, если 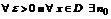 (вообще говоря зависящее от x), такой что
(вообще говоря зависящее от x), такой что 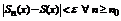 .
.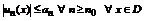 , причем ряд
, причем ряд 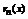 n -ый частичный остаток
n -ый частичный остаток 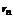 n-ый частичный остаток
n-ый частичный остаток 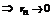 , т.е.
, т.е. 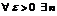 (не зависящее от x) такой что
(не зависящее от x) такой что 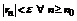 .
.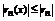 ;
; 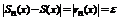
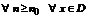 . Ряд сходится равномерно на D.
. Ряд сходится равномерно на D.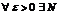 (не зависящий от x) такой что
(не зависящий от x) такой что 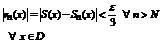 . Пусть
. Пусть 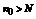 , для
, для 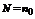 условие выполняется.
условие выполняется.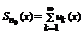 непрерывна на множестве D. Как конечная сумма непрерывных функций. Для любого
непрерывна на множестве D. Как конечная сумма непрерывных функций. Для любого 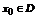 и для выбранного
и для выбранного 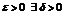 такое что
такое что 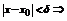
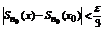 (определение непрерывности
(определение непрерывности 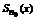 ).
).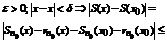
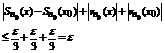 .
.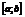 , то его можно почленно интегрировать по любому отрезку
, то его можно почленно интегрировать по любому отрезку 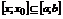 и справедливо равенству
и справедливо равенству 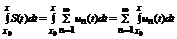 , причем последний ряд сходится равномерно на отрезке
, причем последний ряд сходится равномерно на отрезке  .
.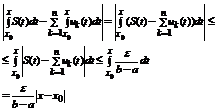
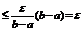 . Справедливо
. Справедливо 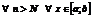 . А это означает, что ряд
. А это означает, что ряд 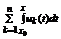 - сходится равномерно на
- сходится равномерно на  .
.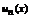 дифференцированы на отрезке и ряд сумма
дифференцированы на отрезке и ряд сумма 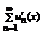 - сходится на
- сходится на 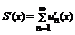 . (*)
. (*)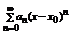 , где
, где 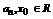 называется степенным рядом по степеням
называется степенным рядом по степеням 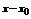 .
.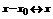 получим ряд
получим ряд 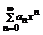 . Исходный получается обратной заменой из данного.
. Исходный получается обратной заменой из данного.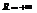 ) такое, что ряд сходится абсолютно при
) такое, что ряд сходится абсолютно при 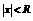 - сходится равномерно при
- сходится равномерно при 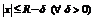 - расходится при
- расходится при 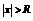 .
.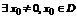 (область сходимости). Так как ряд
(область сходимости). Так как ряд 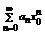 - сходится, то согласно признаку сходимости общий член ряда
- сходится, то согласно признаку сходимости общий член ряда 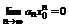 . Это означает, что последовательность
. Это означает, что последовательность 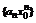 , будучи сходящейся, ограничена, т.е.
, будучи сходящейся, ограничена, т.е. 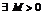 , так что
, так что 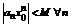
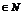 пусть x такой, что
пусть x такой, что 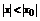 .
. 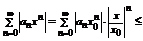 (в силу оценок полученных выше)
(в силу оценок полученных выше) 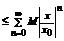 - сходится как сумма геометрической прогрессии (
- сходится как сумма геометрической прогрессии (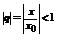 ).
).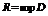 (D - область сходимости).
(D - область сходимости).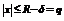 , то
, то 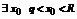 . Тогда получаем, что
. Тогда получаем, что 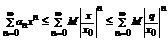 - мажоритарный ряд для
- мажоритарный ряд для 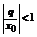 ). Значит данный ряд сходится равномерно в указанной области согласно признаку Вейерштрасса.
). Значит данный ряд сходится равномерно в указанной области согласно признаку Вейерштрасса.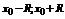 ).
). ).
).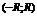 - интервал сходимости:
- интервал сходимости: 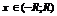 .
. 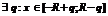 . По теореме Абеля ряд сходится равномерно на
. По теореме Абеля ряд сходится равномерно на 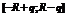 и, значит, сумма его непрерывна во всех точках данного отрезка, в частности, в точке x.
и, значит, сумма его непрерывна во всех точках данного отрезка, в частности, в точке x.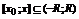 степенного ряда не имеет его радиуса сходимости.
степенного ряда не имеет его радиуса сходимости.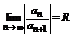 . Рассмотрим ряд полученный почленным дифференцированием ряда
. Рассмотрим ряд полученный почленным дифференцированием ряда 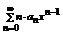 .
.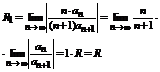 .
.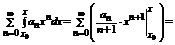
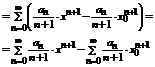 .
.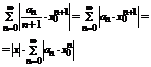 сходится, т.к.
сходится, т.к. 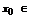 интервалу сходимости.
интервалу сходимости.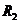 (радиус сходимости первого ряда).
(радиус сходимости первого ряда). 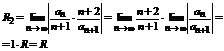 .
.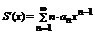 .
. .
.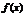 - бесконечно дифференцирован в окрестности точки
- бесконечно дифференцирован в окрестности точки 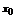 (т.е существует производная). Поставим этой функции в соответствие ряд
(т.е существует производная). Поставим этой функции в соответствие ряд 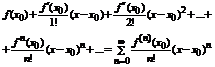 . Данный ряд называется рядом Тейлора функции
. Данный ряд называется рядом Тейлора функции 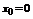 , получаем
, получаем 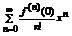 - ряд Маклорена функции
- ряд Маклорена функции 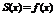 на
на 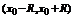 то говорят, что функция
то говорят, что функция 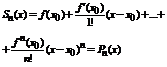 , которые есть ничто иное, как многочлены Тейлора (обозначим их через P (x)).
, которые есть ничто иное, как многочлены Тейлора (обозначим их через P (x)).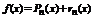 , где
, где 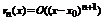 - оценка остатка в форме Пеана, а также
- оценка остатка в форме Пеана, а также 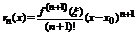 , где точка
, где точка 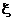 расположена между x 0 и x. Оценка остатка формулы Тейлора в форме Лагранжа.
расположена между x 0 и x. Оценка остатка формулы Тейлора в форме Лагранжа.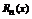 - остаток ряда Тейлора. Вообще говоря
- остаток ряда Тейлора. Вообще говоря 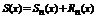 и формула Тейлора
и формула Тейлора 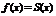 , т.е. функция
, т.е. функция 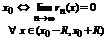 .
.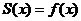 , а это в свою очередь
, а это в свою очередь 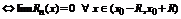 .
.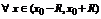 , все производные функции
, все производные функции 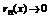 . Применим формулу Лагранжа, для оценки остатка формулы Тейлора. Имеем:
. Применим формулу Лагранжа, для оценки остатка формулы Тейлора. Имеем: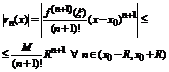 .
.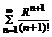 - сходится по признаку Д’Аламбера, то согласно необходимому признаку сходимости. Предел
- сходится по признаку Д’Аламбера, то согласно необходимому признаку сходимости. Предел 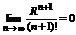 .
.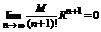 . Следовательно ввиду оценки и
. Следовательно ввиду оценки и 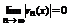 .
.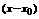 - сходится к функции
- сходится к функции 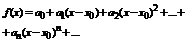 Согласно свойствам степенной ряд можно любое количество раз почленно дифференцировать в окрестности точки
Согласно свойствам степенной ряд можно любое количество раз почленно дифференцировать в окрестности точки 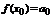 .
.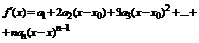
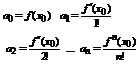 .
.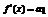
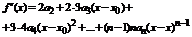
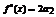 ……………
……………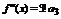
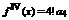 ………………
………………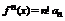 .
.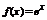 .
.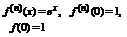 .
.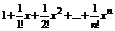 (*)
(*)
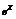 для любого x.
для любого x.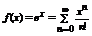 - расходится на R.
- расходится на R.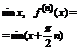
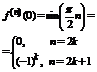
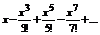
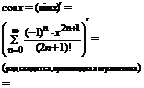
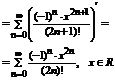 .
.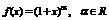
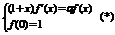 - дифференциальное уравнение, с начальным условием.
- дифференциальное уравнение, с начальным условием.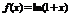
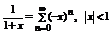
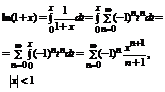 .
.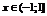 .
.


