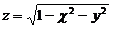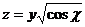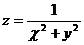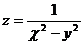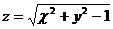КОНТРОЛЬНЫЕ ЗАДАНИЯ С
МЕТОДИЧЕСКИМИ РЕКОМЕНДАЦИЯМИ
ВЫСШАЯ МАТЕМАТИКА
Методическое пособие
(для студентов всех специальностей заочной формы обучения)
Часть I
Альметьевск, 2008 г.
УДК
А.Т. Шляхов, А.Г. Шляхова, Т.А. Бродская, И.М. Зарипова, З.Ф. Зарипова,
Л.Н. Ларина, Р.П. Лазарева, Г.Е. Юдина.
« Контрольные задания с методическими рекомендациями» по курсу высшей математики: Методическое пособие. – Альметьевск: Альметьевский государственный нефтяной институт, 2008. – 53 с.
Методическое пособие «Контрольные задания с методическими рекомендациями» по курсу высшей математики. Часть I. предназначеное для изучения соответствующих разделов высшей математики для студентов всех специальностей заочной формы обучения. Пособие содержит решённые примеры, 30 вариантов контрольных работ.
Печатается по решению учебно-методического совета АГНИ.
Рецензенты:
Декан ФИМ, зав кафедрой «ТХНГ», д.т.н., профессор М.М. Алиев
Зав. кафедрой информатики, к.п.н., доцент Иванов А.Ф.
© Альметьевский государственный
нефтяной институт, 2008
Содержание
1. Введение. Правила выполнения и оформления контрольных работ……4
2. Контрольная работа №1. Элементы линейной и векторной алгебры…...5
3. Контрольная работа №2. Аналитическая геометрия: прямая и плоскость и кривые второго порядка. Уравнение линии в полярных координатах…14
4. Контрольная работа №3. Пределы. Дифференциальное исчисление функции одной переменной. Исследование функций и построение их графиков……………………………………………………………………23
5. Контрольная работа №4. Функции многих переменных………………..41
6. Список рекомендуемой и использованной литературы…………………53
ВВЕДЕНИЕ
ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ КОНТРОЛЬНЫХ РАБОТ
При выполнении контрольных работ необходимо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.
1. Каждая контрольная работа должна быть выполнена в отдельной тетради в клетку чернилами любого цвета, кроме красного. Необходимо оставлять поля шириной 4—5 см для замечаний рецензента.
2. В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), название дисциплины, номер контрольной работы; здесь же следует указать название учебного заведения, дату отсылки работы в институт и адрес студента. В конце работы следует поставить дату ее выполнения и подпись студента.
3. В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту. Контрольные работы, содержащие не все задачи задания, а также задачи не своего варианта, не зачитываются.
4. Решения задач надо располагать в порядке возрастания их номеров, указанных в заданиях, сохраняя номера задач.
5. Перед решением каждой задачи необходимо полностью выписать ее условие. В том случае, если несколько задач, из которых студент выбирает задачи своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными, взятыми из соответствующего номера.
6. Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые рисунки.
7. После получения прорецензированной работы, как незачтенной так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все рекомендации рецензента.
Если рецензент предлагает внести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок.
В случае незачета работы и отсутствия прямого указания рецензента о том, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.
При высылаемых исправлениях должна обязательно находиться прорецензированная работа и рецензия на нее. Поэтому рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после ее рецензирования запрещается.
Контрольная работа №1
Задание 3.
1. Векторы  и
и 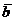 образуют угол φ = 60°, при этом
образуют угол φ = 60°, при этом  , а
, а  . Найти
. Найти  и
и  .
.
2. Вектор  направлен противоположно вектору
направлен противоположно вектору  (6;-9;12) и
(6;-9;12) и  , найти сумму координат вектора
, найти сумму координат вектора  ?
?
3. Найти работу равнодействующей сил  и
и  при перемещении ее точки приложения из начала координат О(0;0;0) в точку М(2;-1;-1). Под каким углом к
при перемещении ее точки приложения из начала координат О(0;0;0) в точку М(2;-1;-1). Под каким углом к  направлена сила
направлена сила  ?
?
4. Если точки А(1;3;2), С(-1;0;2) и Д(5;-4;1) являются вершинами параллелограмма АВСД, то чему равна длина диагонали ВД?
5. Найдите  , если
, если  ,
,  и
и  .
.
6. В параллелограмме АВСД заданы  (2;-1;4),
(2;-1;4),  (-3;2;1), А(5;-3;2), найти сумму координат точки С?
(-3;2;1), А(5;-3;2), найти сумму координат точки С?
7. Вектор  направлен противоположно вектору
направлен противоположно вектору  (6;-12;18) и
(6;-12;18) и  , найти сумму координат вектора
, найти сумму координат вектора  ?
?
8. Точки А(2;-3;5), В(1;-4;6) и Д(3;6;4) являются вершинами ромба АВСД, то длина АС равна?
9. Найдите  , если
, если  ,
,  и
и 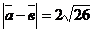 .
.
10. Найдите  , если
, если  ,
,  и
и  .
.
11. Найти длину вектора  , если
, если  ,
,  .
.
12. При каком значении m векторы  и
и  будут коллинеарны?
будут коллинеарны?
13. Найти косинус внутреннего угла А в треугольнике АВС с вершинами А(-1; 2; 3), В(2; -1; 0), С(-4; 2; -3).
14. При каких значениях m длины векторов  и
и  будут равны?
будут равны?
15. Найти скалярное произведение векторов  и
и  , если
, если  ,
,  .
.
16. Даны точки А(-1;2;2), В(4;2;2). Найти длину вектора  .
.
17. При каком значении m векторы  и
и  перпендикулярны?
перпендикулярны?
18. Какую работу производит сила  = (2;-1;-4), приложенная к телу, при его прямолинейном перемещении из точки А(1;-2;3) в точку В(5;-6;1). Под каким углом к
= (2;-1;-4), приложенная к телу, при его прямолинейном перемещении из точки А(1;-2;3) в точку В(5;-6;1). Под каким углом к 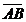 направлена сила
направлена сила  ?
?
19. Найти сумму значений α и β, при которых векторы  и
и  коллинеарны.
коллинеарны.
20. Даны вершины треугольника АВС: А(1;-1;2), B(5;-6;2), С(1;3;-1). Найти длину его высоты, опущенной из вершины В на сторону АС.
21. При каком значении m  , если
, если 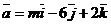 ?
?
22. Даны векторы,  ,
, 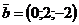 ,
,  . Найти косинус угла между векторами
. Найти косинус угла между векторами  и
и  .
.
23. Даны вершины треугольника АВС: А(0;1;0), B(3;4;-1), С(-2;-3;0). M - точка пересечения медиан треугольника ABC. Найти модуль вектора  .
.
24. Доказать, что четыре точки А1(3;5;1), А2(2;4;7), А3(1;5;3) и А4(4;4;5) лежат в одной плоскости.
25. Даны вершины пирамиды А(5;1;-4), В(1;2;-1), C(3;3;-4), S(2;2;2). Найти длину высоты, опущенной из вершины S на грань АВС.
26. Сила F(2;-4;5) приложена к точке О(0;2;1).Определить модуль момента силы 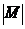 относительно точки А(-1;2;3). Под каким углом к ОА направлена сила F?
относительно точки А(-1;2;3). Под каким углом к ОА направлена сила F?
27. Даны два вектора  и
и  , для которых
, для которых  ,
,  ,
,  . Найти модуль векторного произведения
. Найти модуль векторного произведения  .
.
28. Найти площадь треугольника с вершинами А(1;2;0), В(3;2;1), С(-2;1;2).
29. Найти площадь треугольника, построенного на векторах  и
и  .
.
30. Найти объем параллелепипеда, построенного на векторах  ,
,  ,
,  .
.
Задание 4. Даны координаты вершин пирамиды А1А2А3А4. Найти:
1) длину ребер A1A2, A1A3, A1A4;
2) угол между ребрами: A1A2 и A1A4;
3) площадь грани A1A2А3;
4) объем пирамиды;
5) длину высоты, опущенной из вершины А4 на грань A1A2А3.
1. А1 (4; 2; 5), А2 (0; 7; 2), А3 (0; 2; 7), А4 (1; 5; 0).
2. А1 (4; 4; 10), А2 (4; 10; 2), А3 (2; 8; 4), А4 (9; 6; 4).
3. А1 (4; 6; 5), А2 (6; 9; 4), А3 (2; 10; 10), А4 (7; 5; 9).
4. А1 (3; 5; 4), А2 (8; 7; 4), А3 (5; 10; 4), А4 (4; 7; 8).
5. А1 (10; 6; 6), А2 (-2; 8; 2), А3 (6; 8; 9), А4 (7; 10; 3).
6. А1 (1; 8; 2), А2 (5; 2; 6), А3 (5; 7; 4), А4 (4; 10; 9).
7. А1 (6; 6; 5), А2 (4; 9; 5), А3 (4; 6; 11), А4 (6; 9; 3).
8. А1 (7; 2; 2), А2 (5; 7; 7), А3 (5; 3; 1), А4 (2; 3; 7).
9. А1 (8; 6; 4), А2 (10; 5; 5), А3 (5; 6; 8), А4 (8; 10; 7).
10. А1 (7; 7; 3), А2 (6; 5; 8), А3 (3; 5; 8), А4 (8; 4; 1).
11. А1 (1; -1; 2), А2 (2; 1; 2), А3 (1; 1; 4), А4 (6; -3; 8).
12. А1 (1; 3; 6), А2 (2; 2; 1), А3 (-1; 0; 1), А4 (-4; 6; -3).
13. А1 (-4; 2; 6), А2 (2; -3; 0), А3 (-10; 5; 8), А4 (-5; 2; -4).
14. А1 (7; 2; 4), А2 (7; -1; -2), А3 (3; 3; 1), А4 (-4; 2; 1).
15. А1 (2; 1; 4), А2 (-1; 5; -2), А3 (-7; -3; 2), А4 (-6; -3; 6).
16. А1 (-1; -5; 2), А2 (-6; 0; -3), А3 (3; 6; -3), А4 (-10; 6; 7).
17. А1 (0; -1; -1), А2 (-2; 3; 5), А3 (1; -5; -9), А4 (-1; -6; 3).
18. А1 (5; 2; 0), А2 (2; 5; 0), А3 (1; 2; 4), А4 (-1; 1; 1).
19. А1 (2; -1; -2), А2 (1; 2; 1), А3 (5; 0; -6), А4 (-10; 9; -7).
20. А1 (-2; 0; -4), А2 (-1; 7; 1), А3 (4; -8; -4), А4 (1; -4; 6).
21. А1 (14; 4; 5), А2 (-5; -3; 2), А3 (-2; -6; -3), А4 (-2; 2; -1).
22. А1 (1; 2; 0), А2 (3; 0; -3), А3 (5; 2; 6), А4 (8; 4; -9).
23. А1 (2; -1; 2), А2 (1; 2; -1), А3 (3; 2; 1), А4 (-4; 2; 5).
24. А1 (1; 1; 2), А2 (-1; 1; 3), А3 (2; -2; 4), А4 (-1; 0; -2).
25. А1 (2; 3; 1), А2 (4; 1; -2), А3 (6; 3; 7), А4 (7; 5; -3).
26. А1 (1; 1; -1), А2 (2; 3; 1), А3 (3; 2; 1), А4 (5; 9; -8).
27. А1 (1; 5; -7), А2 (-3; 6; 3), А3 (-2; 7; 3), А4 (-4; 8; -12).
28. А1 (-3; 4; -7), А2 (1; 5; -4), А3 (-5; -2; 0), А4 (2; 5; 4).
29. А1 (-1; 2; -3), А2 (4; -1; 0), А3 (2; 1; -2), А4 (3; 4; 5).
30. А1 (4; -1; 3), А2 (-2; 1; 0), А3 (0; -5; 1), А4 (3; 2; -6).
Контрольная работа №2
Задание 1.
1. Уравнение прямой  записать в каноническом и параметрическом видах.
записать в каноническом и параметрическом видах.
2. Написать уравнение прямой, проходящей через точку пересечения прямых х + 4у – 5 = 0 и 7х + 5у + 11 = 0 и точку А(5;0).
3. Написать уравнение прямой, проходящей через точку А(2;-3;-4) и параллельно прямой:  .
.
4. Доказать что прямые l1 и l2 параллельны,
 .
.
5. Определить угол φ, образованный двумя прямыми: 3х – у + 5 = 0 и
2х + у – 7 = 0.
6. Написать каноническое уравнение прямой, проходящей через точку А(2;0;-1) параллельно прямой х = -2 + t, у = 2t, z = 1-t/2.
7. Показать, что прямая  лежит в плоскости
лежит в плоскости
х+2у–4z+1=0.
8. Составить параметрические уравнения прямой, проходящей через точки А(-5;3;-2) и В(-3;2;-2).
9. Составить параметрические уравнения прямой, проходящей через точку М1(-2;3;5) перпендикулярно плоскости 3х + 5у – 6z – 11 = 0.
10. Найти угол между прямой  и плоскостью 3х+2у–4z+12=0.
и плоскостью 3х+2у–4z+12=0.
11. Дана прямая 2х + 3у + 4 = 0. Составить уравнение прямой, проходящей через точку М0(2;1) под углом в  к данной прямой.
к данной прямой.
12. Найти угол между прямыми: 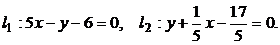
13. Найти точку пересечения прямой и плоскости:  ;
;
14. Написать уравнение плоскости, параллельной плоскости х-2у+2z+5=0 и удаленной от точки М(3;4;-2) на расстоянии d = 5.
15. Доказать что прямые l1 и l2 параллельны
 .
.
16. Написать уравнение прямой, проходящей через точку пересечения прямых х + 2у + 3 = 0, 2х + 3у + 4 = 0, параллельно прямой 5х + 8у = 0.
17. Найти точку пересечения прямой и плоскости: 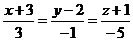
х – 2у + z – 15 = 0.
18. Написать уравнение плоскости, проходящей через точку Р(2;0;-1) и точку М(1;-1;3), перпендикулярно к плоскости 3х + 2у – z = 15.
19. Из точки А(-1;-1;4) опущен на плоскость перпендикуляр; его основание В(2;4;5). Найти уравнение плоскости и уравнение перпендикуляра.
20. Найти угол между плоскостями α и β, если α: х – у + 1 = 0, β: у – z+1=0.
21. Составить уравнение плоскости, проходящей через т. М1(2;3;-1) и М2(1;0;3), перпендикулярно плоскости 3х – у + 3z + 2 = 6.
22. Составить уравнение плоскости, проходящей через прямую:  и точку М(2;-3;-4).
и точку М(2;-3;-4).
23. Составить уравнение плоскости, проходящей через две точки А(-2;1;-3) и В (1;3;-2), параллельной вектору  = (-2;2;-1).
= (-2;2;-1).
24. Составьте уравнение плоскости, которая проходит через точку
А(2;-1;1) перпендикулярно к двум плоскостям 2х – z + 1 = 0 и у = 0.
25. Написать уравнение плоскости, проходящей через точки М1(1;1;1) и М2(-1;1;-1) параллельно прямой, соединяющей точки А(5;-2;3) и В(6;1;0).
26. Написать уравнение плоскости, проходящей через точку М0(2;-1;-3), перпендикулярно линии пересечения плоскостей х+у–z+5=0, 2х–у+2z–2=0.
27. Написать уравнение плоскости, проходящей через прямую  и точку М0(4;-3;2).
и точку М0(4;-3;2).
28. Написать уравнение плоскости, проходящей через точку М0(2;-3;1) параллельно векторам  ,
,  .
.
29. Написать уравнение плоскости, проходящей через пару параллельных прямых  и
и  .
.
30. Написать уравнение плоскости, проходящей через точку А(1;-2;4) и перпендикулярно к прямой  .
.
Задание 2.
1. Уравнение одной из сторон квадрата х + 3у – 5 = 0. Составить уравнения трех остальных сторон квадрата, если Р(-1;0) - точка пересечения его диагоналей. Сделать чертеж.
2. Даны уравнения одной из сторон ромба х – 3у + 10 = 0 и одна из его диагоналей х + 4у - 4 = 0; диагонали ромба пересекаются в точке Р(0;1). Найти уравнения остальных сторон ромба. Сделать чертеж.
3. Уравнения двух сторон параллелограмма х + 2y + 2 = 0 и х + у – 4 = 0, а уравнение одной из его диагоналей х - 2 = 0. Найти координаты вершин параллелограмма. Сделать чертеж.
4. Даны две вершины А(-3;3), В(5;-1) и точка D(4;3) пересечения высот треугольника. Составить уравнения его сторон. Сделать чертеж.
5. Даны вершины А(-3;-2), В(4;-1), С(1;3) трапеции АВCD (AD||BC). Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины D этой трапеции. Сделать чертеж.
6. Даны уравнения двух сторон треугольника 5х – 4у + 15 = 0 и 4х+y–9=0. Его медианы пересекаются в точке Р(0;2). Составить уравнение третьей стороны треугольника. Сделать чертеж.
7. Даны две вершины А(2;-2) и В(3;-1) и точка Р(1;0) пересечения медиан треугольника ABC. Составить уравнение высоты треугольника, проведенной через третью вершину С. Сделать чертеж.
8. Даны уравнения двух высот треугольника x + y = 4 и у=2х и одна из его вершин А(0;2). Составить уравнения сторон треугольника. Сделать чертеж.
9. Даны уравнения двух медиан треугольника х – 2у+1=0 и у - 1=0 и одна из его вершин А(1;3). Составить уравнения его сторон. Сделать чертеж.
10. Две стороны треугольника заданы уравнениями 5х-2у-8=0 и 3х-2у–8=0, а середина третьей стороны совпадает с началом координат. Составить уравнение этой стороны. Сделать чертеж.
11. Составить уравнение и построить линию, расстояния каждой точки которой от начала координат и от точки А (5;0) относятся как 2:1.
12. Составить уравнение и построить линию, расстояние каждой точки которой от точки А(-1;0) вдвое меньше расстояния ее от пряной х = -4.
13. Составить уравнение и построить линию, расстояния каждой точки которой от точки А(2;0) и от прямой 5х + 8 = 0 относятся, как 5:4.
14. Составить уравнение и построить линию, каждая точка которой находится вдвое дальше от точки А(4;0), чем от точки В(1;0).
15. Составить уравнение и построить линию, расстояния каждой точки которой от точки А(2;0) и от пряной 2х + 5 = 0 относятся, как 4:5.
16. Составить уравнение и построить линию, расстояние каждой точки которой от точки А(3;0) вдвое меньше расстояния от точки В (26;0).
17. Составить уравнение и построить линию, каждая точка которой одинаково удалена от точки А(0;2) и от прямой у – 4 = 0.
18. Составить уравнение и построить линию, каждая точка которой равноотстоит от оси ординат и от окружности х2 + у2 = 4х.
19. Составить уравнение и построить линию, каждая точка которой равноудалена от точки А(2;6) и от прямой у + 2 = 0.
20. Составить уравнение и построить линию, каждая точка которой отстоит от точки А(-4;0) втрое дальше, чем от начала координат.
21. В равнобедренном треугольнике АВС заданы вершины С(4;3), уравнение 2х – у – 5 = 0 основания АС и уравнение х – у = 0 боковой стороны (АВ). Написать уравнение стороны ВС.
22. Даны вершины треугольника: А(0;1), В(6;5), С(12;-1). Написать уравнение высоты треугольника, проведённой из вершины (А). Найти величину угла (А).
23. Даны вершины треугольника А(2;3), В(1;-2) и С(-3;2). Составить уравнение медианы (АD).
24. В треугольнике АВС координаты вершины В (2;-7). Уравнение высоты, опущенной из вершины А: 3х + у + 11 = 0. Написать уравнение стороны ВС.
25. Даны две вершины треугольника АВС А(-10;2), В(6;4), его высоты пересекаются в точке О(5;2). Определить координаты третьей вершины треугольника.
26. В равнобедренном треугольнике АВС заданы вершины С(4;3), уравнение 2х – у – 5 = 0 основания АС и уравнение х – у = 0 боковой стороны АВ. Написать уравнение стороны ВС.
27. Даны вершины треугольника: А(0;1), В(6;5), С(12;-1). Написать уравнение высоты треугольника, проведённой из вершины (А). Найти величину угла А.
28. В треугольнике АВС координаты вершины В(2;-7). Уравнение высоты, опущенной из вершины А: 3х + у + 11 = 0. Написать уравнение стороны ВС.
29. Даны вершины треугольника А(1;4), В(3;-9), С(-5;2). Определить длину его медианы, проведенной из вершины В.
30. Даны вершины треугольника А(3;6), В(-1;3), С(2;-1). Вычислить длину его высоты, проведенной из вершины С.
Задание 3.
1. Найти координаты центра и радиус окружности x2 + y2 – 4x +8у – 16 =0.
2. Найти координаты центра и радиус окружности 9x2+9y2–42x-54у–95=0.
3. Найти координаты центра и радиус окружности x2 + y2 – 4x + 6у – 3 = 0.
4. Найти координаты центра и радиус окружности x2 + y2 – x + 2у – 1 = 0.
5. Составить каноническое уравнение окружности, если ее центр лежит в точке С(-4;5) и окружность проходит через точку М(-1;1).
6. Составить уравнение хорды окружности x2 + y2 = 49, делящейся в точке А(1;2) пополам.
7. Составить каноническое уравнение окружности, проходящей через точки А(5;0) и В(1;4), если ее центр лежит на прямой х + у – 3 = 0.
8. Преобразовать уравнение 4x2 + 3y2 – 8x + 12y – 32 = 0 в каноническое уравнение эллипса, найти его полуоси, координаты центра и эксцентриситет. Построить линию.
9. Составить каноническое уравнение эллипса, зная, что расстояние между фокусами 2с = 10, а большая ось 2а = 16. Построить линию.
10. Составить каноническое уравнение эллипса, зная, что малая полуось в=4, а расстояние между фокусами 2с = 10. Построить линию.
11. Составить каноническое уравнение эллипса, зная, что большая полуось
а = 12, а эксцентриситет ε = 0,5. Построить линию.
12. Составить каноническое уравнение эллипса, зная, что сумма полуосей
а + в = 12, а расстояние между фокусами  . Построить линию.
. Построить линию.
13. Найти длины осей, координаты фокусов и эксцентриситет эллипса
4x2 + 9y2 = 144. Построить линию.
14. Составить уравнение эллипса, проходящего через точки  и
и  . Построить линию.
. Построить линию.
15. Составить каноническое уравнение эллипса, фокусы которого расположены на оси Ох, симметрично относительно начала координат, зная что точка  принадлежат эллипсу, а эксцентриситет эллипса
принадлежат эллипсу, а эксцентриситет эллипса 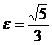 . Построить линию.
. Построить линию.
16. Преобразовать уравнение 3x2 + 12x - y2 + 9 = 0 в каноническое уравнение гиперболы, найти ее полуоси, координаты фокусов, уравнения асимптот. Построить линию.
17. Уравнение асимптот гиперболы у = ±х/2, а расстояние между фокусами 2с=10. Найти каноническое уравнение гиперболы. Построить линию.
18. Составить каноническое уравнение гиперболы, фокусы которой находятся в точках F1(-2,4) и F2(12,4), а длина мнимой оси 26 = 6. Построить линию.
19. Составить каноническое уравнение гиперболы с фокусами на оси Ох, проходящей через точки М1(6,-1) и  . Построить линию.
. Построить линию.
20. Дано уравнение гиперболы 5x2 - 4y2 = 20. Найти: длины ее полуосей; координаты фокусов; эксцентриситет гиперболы; уравнение асимптот. Построить линию.
21. Эксцентриситет гиперболы 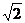 . Составить каноническое уравнение гиперболы, проходящей через точку
. Составить каноническое уравнение гиперболы, проходящей через точку 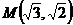 . Построить линию.
. Построить линию.
22. Составить каноническое уравнение гиперболы, если ее фокусы лежат на оси Оу и расстояние между ними 2с = 10, а длина действительной оси 26=8. Построить линию.
23. Найти вершину, фокус и директрису параболы у = -2x2 + 8х – 5. Построить график.
24. Дано уравнение гиперболы 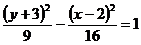 . Найти: длины ее полуосей; координаты фокусов; эксцентриситет гиперболы; уравнение асимптот. Построить линию.
. Найти: длины ее полуосей; координаты фокусов; эксцентриситет гиперболы; уравнение асимптот. Построить линию.
25. Найти вершину, фокус и директрису параболы у2 + 4у - 24х + 76 = 0. Построить график.
26. Найти вершину, фокус и директрису параболы х = 5у2 – 10у + 6. Построить график.
27. К параболе у2 = 4х проведена касательная параллельно прямой
2х – у + 7 = 0. Найти уравнение этой касательной.
28. Камень, брошенный под углом к горизонту, достиг наибольшей высоты 16 м. Описав параболическую траекторию, он упал в 48 м от точки бросания. На какой высоте находился камень на расстоянии 6 м по горизонтали от точки бросания?
29. К параболе у2 = 36х проведены из точки А(1;10) две касательные. Составить уравнение хорды, соединяющей точки касания.
30. Найти уравнение касательной к параболе у2 = 4х, проведенной из точки А(-2;-1).
Задание 4.
Линия задана уравнением r = r(φ) в полярной системе координат, где r ≥ 0. Требуется: 1) построить линию по точкам начиная от φ = 0 до φ = 2π и придавая φ значения с шагом π/8; 2) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс - с полярной осью; 3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия. Построить линию.
1. r = 1/(1 + cosφ)
2. r = 4/(2 - 3cosφ)
3. r = 1/(2 + 2cosφ)
4. r = 10/(2 + cosφ)
5. r = 1/[3(1 - cosφ)]
6. r = 1/(2 + cosφ)
7. r = 8/(3 - cosφ)
8. r = 5/(3 - 4cosφ)
9. r = 3/(1 - 2cosφ)
10. r = 5/(6 + 3cosφ)
11. r = 2cos2φ
12. r = 2(1 + cosφ)
13. r = 2sin2φ
14. 
15. 
16. r = 2cos3φ
17. r = 2 + cosφ
18. r = 3(1 + cosφ)
19. r = 2sinφ
20. r = 6cosφ
21. r = cosφ – sinφ
22. r = cosφ + sinφ
23. r = 3/(1 + sinφ)
24. r = 15/(3 - 4cosφ)
25. r = 4/(1 - cosφ)
26. r = 16/(5 - 3cosφ)
27. r = 16/(5 + 3cosφ)
28. r = 9/(4 - 5cosφ)
29. r = 12/(2 - cosφ)
30. r = 10/(2 + sinφ)
Задание 1.
а) Найти острый угол между двумя плоскостями 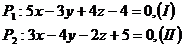 .
.
Решение: Угол между двумя плоскостями 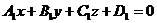 и
и 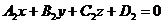 равен углу между их нормальными векторами
равен углу между их нормальными векторами 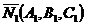 и
и 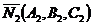 и определяется по формуле
и определяется по формуле
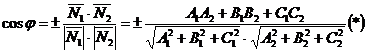 .
.
Из формулы (*) получим, если учесть, что на основании уравнения (I) А1 = 5; В1 = 3; С1 = 4, а из (II) А2 = 3; В2 = -4; С2 = -2, 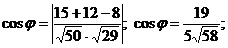
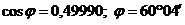 . В формуле (*) следует взять абсолютную величину правой части, так как надо найти острый угол между плоскостями.
. В формуле (*) следует взять абсолютную величину правой части, так как надо найти острый угол между плоскостями.
б) Составить уравнение плоскости, которая проходит через прямую пересечения плоскостей Р1, Р2 и точку М(2,-1,3).
Решение: Две пересекающиеся плоскости Р1 и Р2 определяют (задают) пучок плоскостей, уравнение которого имеет вид 5x–3y+4z–4+t (3x–4y–2z+5)=0, где t – параметр. Все плоскости этого пучка проходят через прямую пересечения плоскостей Р1 и Р2 (ось пучка). Из множества плоскостей пучка выбираем ту (определяем значение t), которая проходит через точку М: значение t должно быть таким, чтобы координаты точки М удовлетворяли уравнению
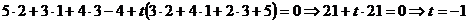 .
.
Уравнение искомой плоскости
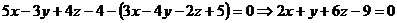 .
.
Задание 2. Даны уравнения высот треугольника 2х – 3у + 1 = 0 и х + у = 0 и координаты одной из его вершин А(1;2). Найти уравнения сторон треугольника.
Решение: Точка А(1;2) не принадлежит данным в условии высотам треугольника, так как ее координаты не удовлетворяют их уравнениям:
2·1 - 3·2 + 1 ≠ 0 и 1 + 2 ≠ 0. Отсюда следует, что высоты, данные в задаче, проведены из двух других вершин треугольника В и С. Назовем их СД и ВЕ, 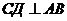 ,
, 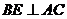 . Пусть высота СД имеет уравнение х + у = 0, а высота ВЕ имеет уравнение 2х – 3у + 1 = 0.
. Пусть высота СД имеет уравнение х + у = 0, а высота ВЕ имеет уравнение 2х – 3у + 1 = 0.
I способ. Так как 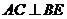 , то уравнение АС мы найдем из уравнения семейства прямых, перпендикулярных ВЕ, приняв во внимание, что искомая прямая проходит через данную точку А(1;2).
, то уравнение АС мы найдем из уравнения семейства прямых, перпендикулярных ВЕ, приняв во внимание, что искомая прямая проходит через данную точку А(1;2).
Если две прямые 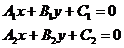 перпендикулярны, то выполняется условие
перпендикулярны, то выполняется условие 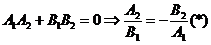 , то есть коэффициенты при х и у меняются местами, а также изменяется знак при у.
, то есть коэффициенты при х и у меняются местами, а также изменяется знак при у.
1. Уравнение стороны АС
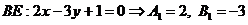
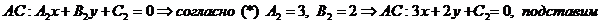
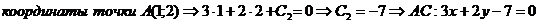
2. Уравнение стороны АВ
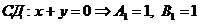
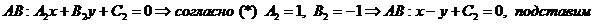
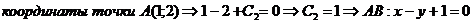
3. Уравнение стороны ВС
Сначала следует найти координаты точек В и С, как точек пересечения прямых ВЕ и АВ и прямых СД и АС, соответственно.
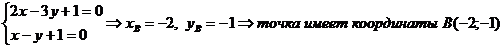
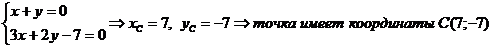
Теперь найдем уравнение ВС, воспользовавшись уравнение прямой, проходящей через две точки В(-2;-1) и С(7;-7).
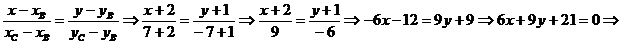
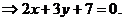
II способ. Если две прямые заданы уравнениями 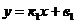 и
и 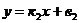 , то условия перпендикулярности двух прямых имеет вид
, то условия перпендикулярности двух прямых имеет вид 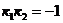 .
.
1. Уравнение стороны АС (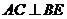 )
)
Определим угловой коэффициент 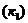 высоты ВЕ. Преобразуем уравнение высоты ВЕ:
высоты ВЕ. Преобразуем уравнение высоты ВЕ: 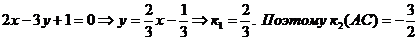 .
.
Уравнение прямой, проходящей через данную точку А(х1;у1) в данном направлении, определяемом угловым коэффициентом, 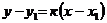 (**).
(**).
Точка А(1;2) принадлежит прямой АС, поэтому подставим ее координаты в уравнение (**). 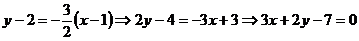 .
.
2. Уравнение стороны АВ (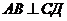 )
)
Угловой коэффициент высоты СД, имеющей вид, 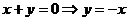 равен
равен 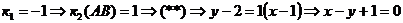 .
.
3. Уравнение стороны ВС рассмотрено выше.
Задание 3. Найти уравнение касательной к параболе у2 = 4х, проведенной из точки А(-2;-1).
Решение: Уравнение прямой будем искать в виде 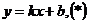 . Так как точка А принадлежит искомой касательной, подставляя ее координаты в уравнение (*), получим тождество
. Так как точка А принадлежит искомой касательной, подставляя ее координаты в уравнение (*), получим тождество 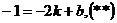 . Далее, прямая (*) и парабола у2 = 4х имеют единственную общую точку (касаются). Следовательно, система уравнений
. Далее, прямая (*) и парабола у2 = 4х имеют единственную общую точку (касаются). Следовательно, система уравнений 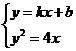 имеет единственное решение. Решаем ее относительно
имеет единственное решение. Решаем ее относительно
х и у. Это можно сделать различными способами, например, возвести правую и левую части первого уравнения в квадрат и подставить в левую часть полученного равенства вместо у2 его выражение из второго уравнения. Получим 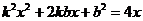 . Это – квадратное уравнение, имеющее единственное решение в случае, когда дискриминант равен нулю. Таким образом,
. Это – квадратное уравнение, имеющее единственное решение в случае, когда дискриминант равен нулю. Таким образом,  . Теперь для параметров k и b прямой (*) имеем два условия: (**) и (***). Следовательно, искомые значения параметров находятся как решения системы из этих условий:
. Теперь для параметров k и b прямой (*) имеем два условия: (**) и (***). Следовательно, искомые значения параметров находятся как решения системы из этих условий:
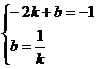 . Подстановкой вместо b в первое уравнение его выражения из второго, получим
. Подстановкой вместо b в первое уравнение его выражения из второго, получим 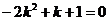 , откуда находим, что
, откуда находим, что 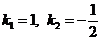 . Система имеет два решения:
. Система имеет два решения: 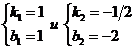 . Следовательно, две прямые удовлетворяют условиям задачи. Их уравнения:
. Следовательно, две прямые удовлетворяют условиям задачи. Их уравнения: 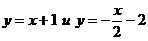 .
.
Задание 4. Постройте кривую 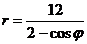 в полярной системе координат. Найти каноническое уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс - с полярной осью.
в полярной системе координат. Найти каноническое уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс - с полярной осью.
Решение: Полярная система координат задана, если заданы точка О, называемая полюсом, и исходящий из полюса луч ОР- полярная ось. Если задать на плоскости прямоугольную декартову систему координат, поместив ее начало в полюс и совместив ось абсцисс с полярной осью, то декартовы координаты х и у будут выражены через полярные координаты (r и φ) уравнениями:
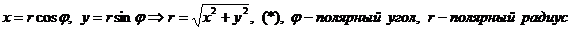 .
.
Составим таблицу для значений r от φ с шагом π/8.
| φ
|
| π/8
| π/4
| 3π/8
| π/2
| 5π/8
| 3π/4
| 7π/8
| π
|
| cosφ
|
| 0,92
| 0,71
| 0,38
|
| -0,38
| -0,71
| -0,92
| -1
|
| r
|
| 11,1
| 9,3
| 7,4
|
|
| 4,4
| 4,1
|
|
| φ
| 9π/8
| 5π/4
| 11π/8
| 3π/2
| 13π/8
| 7π/4
| 15π/8
| 2π
|
|
| cosφ
| -0,92
| -0,71
| -0,38
|
| 0,38
| 0,71
| 0,92
|
|
|
| r
| 4,1
| 4,4
|
|
| 7,4
| 9,3
| 11,1
|
|
|
Примем произвольный отрезок за единицу масштаба, которым мы будем пользоваться при построении r. Для построения проводим из полюса лучи, соответствующие выбранным значениям φ, и на каждом луче (то есть вдоль него) откладываем соответствующие вычисленные значения полярного радиуса. Полученные точки соединяем плавной кривой. Построенная линия – эллипс.
Найдем каноническое уравнение данной линии в декартовой прямоугольной системе координат, используя уравнения, отмеченные выше (*).
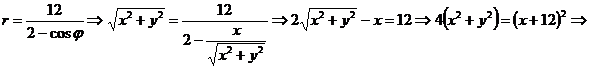
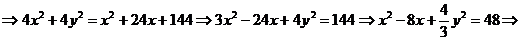
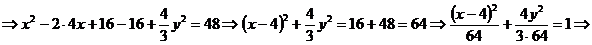
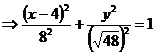 .
.
Это уравнение определяет эллипс с полуосями 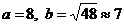 и с центром симметрии О(4,0).
и с центром симметрии О(4,0).
Контрольная работа №3
Контрольная работа №4
Функции многих переменных.
Задание 1. Найти области определения функций.
1. 
2. 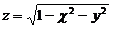
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 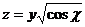
12. 
13. 
14. 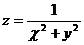
15. 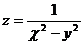
16. 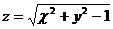
17. 
|
|
|



 и
и 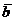 образуют угол φ = 60°, при этом
образуют угол φ = 60°, при этом  , а
, а  . Найти
. Найти  и
и  .
. направлен противоположно вектору
направлен противоположно вектору  (6;-9;12) и
(6;-9;12) и  , найти сумму координат вектора
, найти сумму координат вектора  и
и  при перемещении ее точки приложения из начала координат О(0;0;0) в точку М(2;-1;-1). Под каким углом к
при перемещении ее точки приложения из начала координат О(0;0;0) в точку М(2;-1;-1). Под каким углом к  направлена сила
направлена сила  ?
? , если
, если  ,
,  и
и  .
. (2;-1;4),
(2;-1;4),  (-3;2;1), А(5;-3;2), найти сумму координат точки С?
(-3;2;1), А(5;-3;2), найти сумму координат точки С? , найти сумму координат вектора
, найти сумму координат вектора  , если
, если  ,
,  и
и 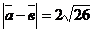 .
. , если
, если  ,
,  и
и  .
. , если
, если  ,
,  .
. и
и  будут коллинеарны?
будут коллинеарны? и
и  будут равны?
будут равны? и
и  ,
,  .
. .
. и
и  перпендикулярны?
перпендикулярны? = (2;-1;-4), приложенная к телу, при его прямолинейном перемещении из точки А(1;-2;3) в точку В(5;-6;1). Под каким углом к
= (2;-1;-4), приложенная к телу, при его прямолинейном перемещении из точки А(1;-2;3) в точку В(5;-6;1). Под каким углом к 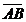 направлена сила
направлена сила  ?
? и
и  коллинеарны.
коллинеарны. , если
, если 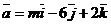 ?
? ,
, 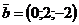 ,
,  . Найти косинус угла между векторами
. Найти косинус угла между векторами  и
и  .
. .
.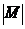 относительно точки А(-1;2;3). Под каким углом к ОА направлена сила F?
относительно точки А(-1;2;3). Под каким углом к ОА направлена сила F? , для которых
, для которых  ,
,  ,
,  . Найти модуль векторного произведения
. Найти модуль векторного произведения  .
. и
и  .
. ,
,  ,
,  .
. записать в каноническом и параметрическом видах.
записать в каноническом и параметрическом видах. .
. .
. лежит в плоскости
лежит в плоскости и плоскостью 3х+2у–4z+12=0.
и плоскостью 3х+2у–4z+12=0. к данной прямой.
к данной прямой.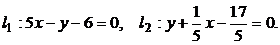
 ;
; .
.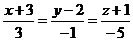
 и точку М(2;-3;-4).
и точку М(2;-3;-4). и точку М0(4;-3;2).
и точку М0(4;-3;2). ,
,  .
. и
и  .
. .
. . Построить линию.
. Построить линию. и
и  . Построить линию.
. Построить линию. принадлежат эллипсу, а эксцентриситет эллипса
принадлежат эллипсу, а эксцентриситет эллипса 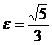 . Построить линию.
. Построить линию. . Построить линию.
. Построить линию.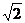 . Составить каноническое уравнение гиперболы, проходящей через точку
. Составить каноническое уравнение гиперболы, проходящей через точку 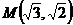 . Построить линию.
. Построить линию.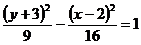 . Найти: длины ее полуосей; координаты фокусов; эксцентриситет гиперболы; уравнение асимптот. Построить линию.
. Найти: длины ее полуосей; координаты фокусов; эксцентриситет гиперболы; уравнение асимптот. Построить линию.

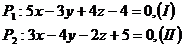 .
.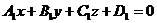 и
и 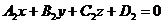 равен углу между их нормальными векторами
равен углу между их нормальными векторами 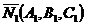 и
и 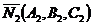 и определяется по формуле
и определяется по формуле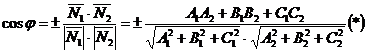 .
.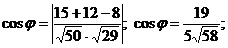
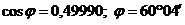 . В формуле (*) следует взять абсолютную величину правой части, так как надо найти острый угол между плоскостями.
. В формуле (*) следует взять абсолютную величину правой части, так как надо найти острый угол между плоскостями.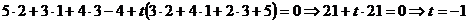 .
.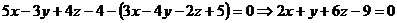 .
.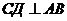 ,
, 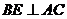 . Пусть высота СД имеет уравнение х + у = 0, а высота ВЕ имеет уравнение 2х – 3у + 1 = 0.
. Пусть высота СД имеет уравнение х + у = 0, а высота ВЕ имеет уравнение 2х – 3у + 1 = 0.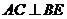 , то уравнение АС мы найдем из уравнения семейства прямых, перпендикулярных ВЕ, приняв во внимание, что искомая прямая проходит через данную точку А(1;2).
, то уравнение АС мы найдем из уравнения семейства прямых, перпендикулярных ВЕ, приняв во внимание, что искомая прямая проходит через данную точку А(1;2).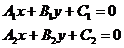 перпендикулярны, то выполняется условие
перпендикулярны, то выполняется условие 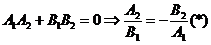 , то есть коэффициенты при х и у меняются местами, а также изменяется знак при у.
, то есть коэффициенты при х и у меняются местами, а также изменяется знак при у.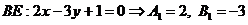
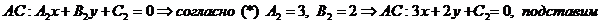
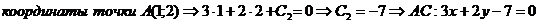
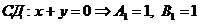
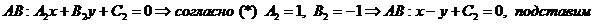
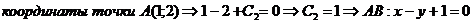
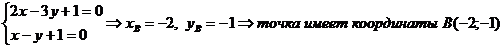
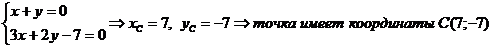
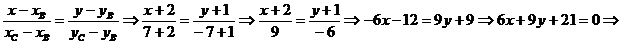
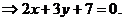
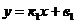 и
и 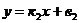 , то условия перпендикулярности двух прямых имеет вид
, то условия перпендикулярности двух прямых имеет вид 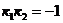 .
.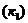 высоты ВЕ. Преобразуем уравнение высоты ВЕ:
высоты ВЕ. Преобразуем уравнение высоты ВЕ: 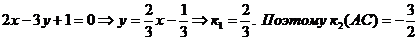 .
.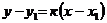 (**).
(**).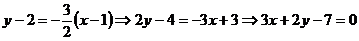 .
.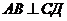 )
)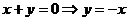 равен
равен 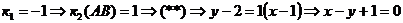 .
.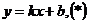 . Так как точка А принадлежит искомой касательной, подставляя ее координаты в уравнение (*), получим тождество
. Так как точка А принадлежит искомой касательной, подставляя ее координаты в уравнение (*), получим тождество 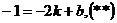 . Далее, прямая (*) и парабола у2 = 4х имеют единственную общую точку (касаются). Следовательно, система уравнений
. Далее, прямая (*) и парабола у2 = 4х имеют единственную общую точку (касаются). Следовательно, система уравнений 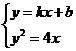 имеет единственное решение. Решаем ее относительно
имеет единственное решение. Решаем ее относительно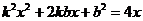 . Это – квадратное уравнение, имеющее единственное решение в случае, когда дискриминант равен нулю. Таким образом,
. Это – квадратное уравнение, имеющее единственное решение в случае, когда дискриминант равен нулю. Таким образом,  . Теперь для параметров k и b прямой (*) имеем два условия: (**) и (***). Следовательно, искомые значения параметров находятся как решения системы из этих условий:
. Теперь для параметров k и b прямой (*) имеем два условия: (**) и (***). Следовательно, искомые значения параметров находятся как решения системы из этих условий: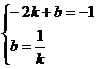 . Подстановкой вместо b в первое уравнение его выражения из второго, получим
. Подстановкой вместо b в первое уравнение его выражения из второго, получим 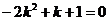 , откуда находим, что
, откуда находим, что 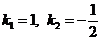 . Система имеет два решения:
. Система имеет два решения: 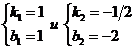 . Следовательно, две прямые удовлетворяют условиям задачи. Их уравнения:
. Следовательно, две прямые удовлетворяют условиям задачи. Их уравнения: 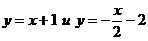 .
.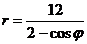 в полярной системе координат. Найти каноническое уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс - с полярной осью.
в полярной системе координат. Найти каноническое уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс - с полярной осью.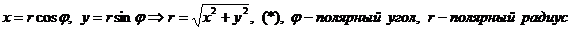 .
.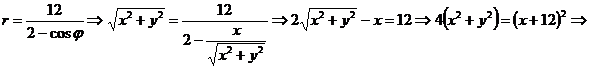
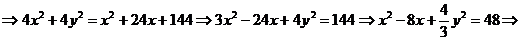
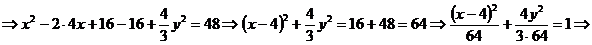
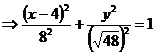 .
.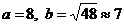 и с центром симметрии О(4,0).
и с центром симметрии О(4,0).