Элементы аналитической геометрии на плоскости.
Теоретические вопросы.
- Как определяются декартовые координаты точки на плоскости?
- Чем отличаются координаты двух точек, симметричных относительно: а) оси Ох; б) оси Оу; в) начала координат.
- Как вычислить расстояние между двумя точками?
- Напишите формулы для координат середины отрезка через координаты его концов.
- Как найти координаты точки пересечения медиан треугольника через координаты его вершин?
- Дайте определение уравнения линии на плоскости.
- Как найти координаты точки пересечения двух линий на плоскости, заданных своими уравнениями?
- Чем отличается уравнение прямой в декартовых координатах от уравнений других линий?
- Напишите формулу для вычисления угла между двумя прямыми.
- Как выглядят условия параллельности и перпендикулярности двух прямых?
- Напишите уравнение прямой, проходящей: а) через заданную точку в заданном направлении; б) через две заданные точки.
- Как написать уравнение медианы, высоты в треугольнике, если известны координаты его вершин?
- Дайте определение окружности.
- Какой вид имеет уравнение окружности с центром в любой точке плоскости хОу; в любой точке оси Ох; в любой точке оси Оу; с центром в начале координат?
Расчетная работа №1.
Решение типового примера.
Даны вершины треугольника АВС: А(-4;8), В(5;-4), С(10;6).
Найти:
1) длину стороны АВ;
2) уравнения сторон АВ и АС и их угловые коэффициенты;
3) угол А в радианах;
4) уравнение высоты СD и ее длину;
5) уравнение окружности, для которой высота СD есть диаметр;
6) систему линейных неравенств, определяющих треугольник АВС.
Решение.
1. Найдем длину стороны АВ.
Расстояние d между точками М1(х 1; у 1) и М2(х 2; у 2) определяется по формуле:
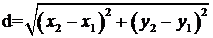 (1)
(1)
Подставив в эту формулу координаты точек А и В, имеем:
АВ= 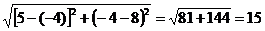
2. Уравнение прямой, проходящей через точки М1(х1; у1) и М2(х2; у2), имеет вид:
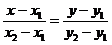 (2)
(2)
Подставив в (2) координаты точек А и В, получим уравнение прямой АВ:
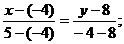

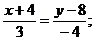
3 у –24 =–4 х –16, 4 х +3 у –8=0 (АВ)
Для нахождения углового коэффициента к АВ прямой АВ, разрешим полученное уравнение относительно у: у = 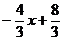 .
.
Отсюда к АВ = 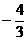 .
.
Подставив в формулу (2) координаты точек А и С, найдем уравнение прямой АС:
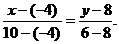
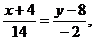
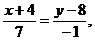
х +7 у –52=0 (АС).
Отсюда к АС = 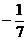 .
.
3. Угол 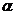 между двумя прямыми, угловые коэффициенты которых равны к 1 и к 2, определяется по формуле:
между двумя прямыми, угловые коэффициенты которых равны к 1 и к 2, определяется по формуле:
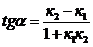 (3)
(3)
Угол А, образованный прямыми АВ и АС, найдем по формуле (3), подставив в нее к 1 = к АВ = 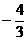 , к 1 = к АС =
, к 1 = к АС = 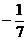 .
.
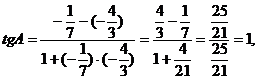
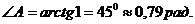
4. Так как высота СD перпендикулярна стороне АВ, то угловые коэффициенты этих прямых обратны по величине и противоположны по знаку, т.е.
к СD = 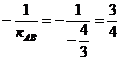 .
.
Уравнение прямой, проходящей через данную точку М1(х1; у1) в заданном направлении, имеет вид:
 (4)
(4)
Подставив в (4) координаты точки С(10;6) и к СD = 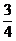 , получим уравнение высоты СD:
, получим уравнение высоты СD:
у – 6 = 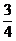 (х – 10), 4 у – 24 = 3 х – 30, 3 х – 4 у – 6 = 0 (СD). (5)
(х – 10), 4 у – 24 = 3 х – 30, 3 х – 4 у – 6 = 0 (СD). (5)
Для нахождения длины СD определим координаты точки D, решив систему уравнений (АВ) и (CD):
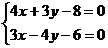 , откуда х = 2, у = 0, то есть D (2; 0)
, откуда х = 2, у = 0, то есть D (2; 0)
Подставив в формулу (1) координаты точек С и D, находим:
СD = 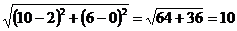 .
.
5. Уравнение окружности радиуса R с центром в точка Е(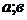 ) имеет вид:
) имеет вид:
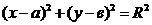 (6)
(6)
Так как СDявляется диаметром искомой окружности, то ее центр Е есть середина отрезка СD. Воспользуемся формулами деления отрезка пополам, получим:
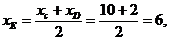
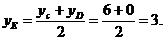
Следовательно, Е(6; 3) и R= 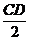 = 5. Используя формулу (6), получаем уравнение искомой окружности:
= 5. Используя формулу (6), получаем уравнение искомой окружности:

6. Множество точек треугольника АВС есть пересечение трех полуплоскостей, первая из которых ограничена прямой АВ и содержит точку С, вторая ограничена прямой ВС и содержит точку А, а третья ограничена прямой АС и содержит точку В.
Для получения неравенства, определяющего полуплоскость, ограниченную прямой АВ и содержащую точку С, подставим в уравнение прямой АВ координаты точки С:
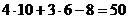 > 0
> 0
Поэтому искомое неравенство имеет вид: 4 х +3 у 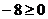 .
.
Для составления неравенства, определяющего полуплоскость, ограниченную прямой ВС и содержащую точку А, найдем уравнение прямой ВС, подставив в формулу (2) координаты точек Ви С:
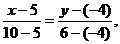
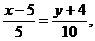
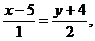
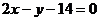 (ВС).
(ВС).
Подставив в последнее уравнение координаты точки А, имеем:
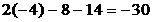 < 0. Искомое неравенство будет 2 х – у – 14
< 0. Искомое неравенство будет 2 х – у – 14 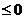 . Подобным образом составим неравенство, определяющее полуплоскость, ограниченную прямой АС и содержащую точку В:
. Подобным образом составим неравенство, определяющее полуплоскость, ограниченную прямой АС и содержащую точку В: 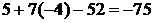 < 0. Третье искомое неравенство будет х +7 у –52
< 0. Третье искомое неравенство будет х +7 у –52 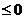 . Итак, множество точек треугольника АВС определяется системой неравенств:
. Итак, множество точек треугольника АВС определяется системой неравенств:
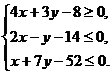
На рис. 1 в декартовой прямоугольной системе координат хОу изображен треугольник АВС, высота СD, окружность с центром в точке Е и диаметром CD
.
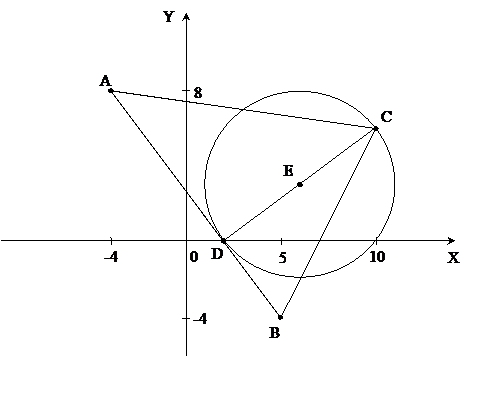
Рис. 1
Элементы линейной алгебры
Теоретические вопросы
- Что называется определителем второго, третьего, n-го порядков?
- Назовите основные свойства определителей.
- Что называется минором, алгебраическим дополнением элемента определителя?
- Назовите методы вычисления определителей третьего, n-го порядков.
- Напишите формулы Крамера решения системы линейных уравнений. В каких случаях их можно использовать?
- Что называется матрицей?
- Как определяются основные действия над матрицами?
- Какая матрица называется обратной по отношению к данной матрице? Как найти матрицу, обратную данной?
- Что называется рангом матрицы? Как найти ранг матрицы?
- Сформулируйте теорему Кронекера-Капелли.
- Опишите матричный способ решения системы линейных уравнений.
- Назовите схему решения системы линейных уравнений по методу Гаусса.
- Какова геометрическая интерпретация системы линейных уравнений и неравенств?
Часть I.
Часть II
Часть III
Часть I
В задачах 1-20 решить данную систему уравнений пользуясь формулами Крамера. Сделать проверку полученного решения.
1. 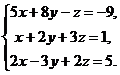 2.
2. 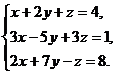
3. 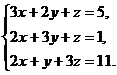 4.
4. 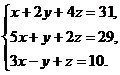
5. 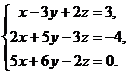 6.
6. 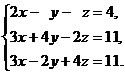
7.  8.
8. 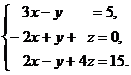
9. 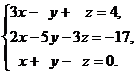 10.
10. 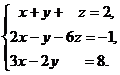
11.  12.
12. 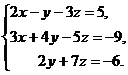
13. 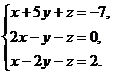 14.
14. 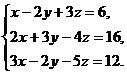
15. 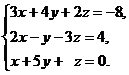 16.
16. 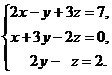
17. 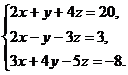 18.
18. 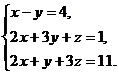
19. 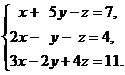 20.
20. 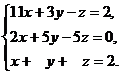
Часть II
В задачах 1-20 систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы. Сделать проверку полученного решения
1. 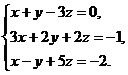 2.
2. 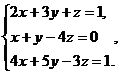
3. 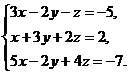 4.
4. 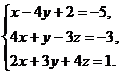
5. 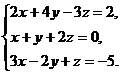 6.
6. 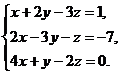
7. 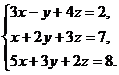 8.
8. 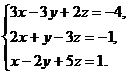
9. 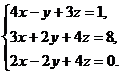 10.
10. 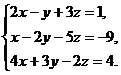
11. 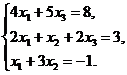 12.
12. 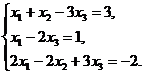
13. 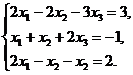 14.
14. 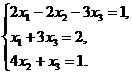
15. 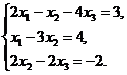 16.
16. 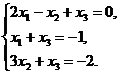
17. 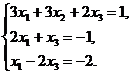 18.
18. 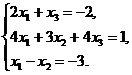
19. 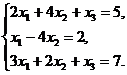 20.
20. 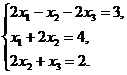
Часть III
В задачах 1-10 решить данную систему уравнений методом Гаусса. Рекомендуется преобразования, связанные с последовательным исключением неизвестных, применять к расширенной матрице данной системы. Сделать проверку полученного решения.
1. 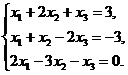 2.
2. 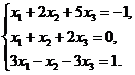
3. 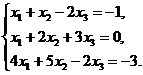 4.
4. 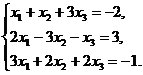
5. 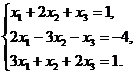 6.
6. 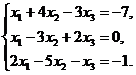
7. 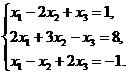 8.
8. 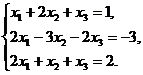
9. 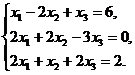 10.
10. 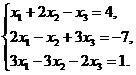
Графический метод.
Несмотря на то, что графический метод решения задач линейного программирования применяется только для задач с двумя искомыми переменными (или в случае трехмерного пространства с тремя), этот метод позволяет понять основную суть линейного программирования.
Задача 1.
Рассмотрим систему неравенств
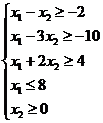 (1)
(1)
и линейную форму
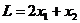 (2)
(2)
Найти минимум и максимум линейной формы (2) из области решений системы (1).
Решение.
Построим выпуклый многоугольник, заданный системой неравенств (1). Для этого построим прямоугольную систему координат х1ох2. Если в этой системе координат построить прямую ах1+bх2=с, то эта прямая разбивает плоскость х1ох2 на две полуплоскости, каждая из которых лежит по одну сторону от прямой. Сама прямая в этом случае называется граничной и принадлежит обеим полуплоскостям. Координаты точек, лежащих в одной полуплоскости удовлетворяют неравенству ах1+вх2≤с, а координаты точек, лежащих в другой полуплоскости, удовлетворяют неравенству ах1+вх2≥с. Построим в плоскости х1ох2 граничные прямые:
1) 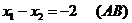 4)
4) 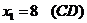
2) 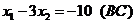 5)
5) 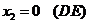
3) 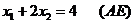
В результате получим пятиугольник АВСDЕ (рис. 2)
Значения х1 и х 2, удовлетворяющие системе неравенств (1), являются координатами точек, лежащих внутри или на границе найденного пятиугольника. Теперь задача сводится к тому, чтобы найти те значения х 1 и х 2 при которых линейная форма L (2) имеет минимум, и те значения х1 и х 2 при которых линейная форма L достигает максимума. Из рис. 2 видно, что координаты всех точек, лежащих внутри или на границе пятиугольника, не являются отрицательными, т.е. все значения х 1 и х 2 больше или равны нулю.

Для каждой точки плоскости х1ох 2 линейная форма L принимает фиксированное значение. Множество точек, при которых линейная форма L принимает фиксированное значение L 1, есть прямая 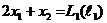 , которая перпендикулярна вектору
, которая перпендикулярна вектору 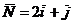 . Если прямую
. Если прямую 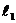 передвигать параллельно самой себе в положительном направлении вектора
передвигать параллельно самой себе в положительном направлении вектора 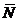 , то линейная форма L будет возрастать, а в противоположном направлении – убывать. Построим прямую
, то линейная форма L будет возрастать, а в противоположном направлении – убывать. Построим прямую 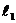 для того случая, когда L = 0, т.е. построим прямую
для того случая, когда L = 0, т.е. построим прямую 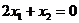 . Как видно из рис. 2, при передвижении прямой
. Как видно из рис. 2, при передвижении прямой 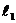 в положительном направлении вектора
в положительном направлении вектора 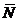 она впервые встречается с вершиной А(0;2) построенного пятиугольника АВСDЕ. В этой вершине линейная форма L имеет минимум. Следовательно,
она впервые встречается с вершиной А(0;2) построенного пятиугольника АВСDЕ. В этой вершине линейная форма L имеет минимум. Следовательно,
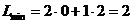 .
.
При дальнейшем передвижении прямой 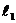 параллельно самой себе в положительном направлении вектора
параллельно самой себе в положительном направлении вектора 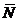 значение линейной формы будет возрастать, и оно достигает максимального значения в точке С(8;6). Таким образом,
значение линейной формы будет возрастать, и оно достигает максимального значения в точке С(8;6). Таким образом,
 .
.
Задача 2.
Туристской фирме требуется не более 10 автобусов грузоподъёмностью 3 тонны и не более 8 автобусов грузоподъёмностью 5 тонн. Цена автобуса первой марки 20000 у.е., цена автобуса второй марки 40000 у.е. Туристская фирма может выделить для приобретения автобусов не более 400000 у.е. Сколько следует приобрести автобусов каждой марки в отдельности, чтобы их общая (суммарная) грузоподъёмность была максимальной.
Решение.
Пусть приобретено х 1 трёхтонных, х 2 пятитонных автобусов, тогда заданные условия задачи можно записать так:
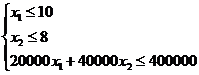 или
или 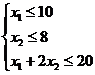 (1)
(1)
Линейная форма L (часто её называют целевой функцией) применительно к условиям нашей задачи имеет вид:
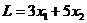 (2)
(2)
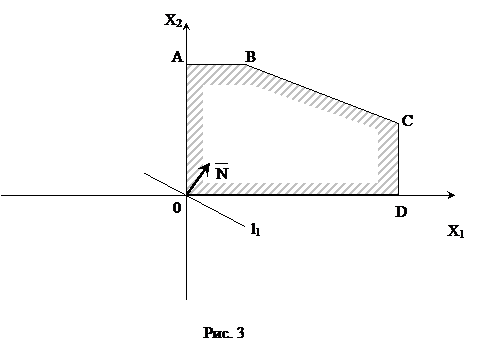
Требуется найти те значения х1 и х 2, при которых L достигает максимального значения. По условию задачи 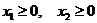 . Решим задачу графическим методом, который был использован при решении задачи 1. Построим многоугольник АВСDЕ (рис. 3), все точки которого удовлетворяют системе неравенств.
. Решим задачу графическим методом, который был использован при решении задачи 1. Построим многоугольник АВСDЕ (рис. 3), все точки которого удовлетворяют системе неравенств.
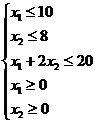 (3)
(3)

Затем построим вектор 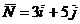 и прямую
и прямую 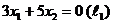 . Перемещая прямую
. Перемещая прямую 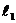 параллельно самой себе в положительном направлении вектора
параллельно самой себе в положительном направлении вектора 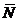 , установим, что L достигает максимального значения в точке С, для которой х 1 = 10 и х2 = 5. Следовательно, туристской фирме следует приобрести 10 трёхтонных и 5 пятитонных автобусов. В этом случае общая грузоподъёмность составит 55 тонн. (
, установим, что L достигает максимального значения в точке С, для которой х 1 = 10 и х2 = 5. Следовательно, туристской фирме следует приобрести 10 трёхтонных и 5 пятитонных автобусов. В этом случае общая грузоподъёмность составит 55 тонн. (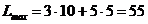 )
)
Элементы аналитической геометрии на плоскости.
Теоретические вопросы.
- Как определяются декартовые координаты точки на плоскости?
- Чем отличаются координаты двух точек, симметричных относительно: а) оси Ох; б) оси Оу; в) начала координат.
- Как вычислить расстояние между двумя точками?
- Напишите формулы для координат середины отрезка через координаты его концов.
- Как найти координаты точки пересечения медиан треугольника через координаты его вершин?
- Дайте определение уравнения линии на плоскости.
- Как найти координаты точки пересечения двух линий на плоскости, заданных своими уравнениями?
- Чем отличается уравнение прямой в декартовых координатах от уравнений других линий?
- Напишите формулу для вычисления угла между двумя прямыми.
- Как выглядят условия параллельности и перпендикулярности двух прямых?
- Напишите уравнение прямой, проходящей: а) через заданную точку в заданном направлении; б) через две заданные точки.
- Как написать уравнение медианы, высоты в треугольнике, если известны координаты его вершин?
- Дайте определение окружности.
- Какой вид имеет уравнение окружности с центром в любой точке плоскости хОу; в любой точке оси Ох; в любой точке оси Оу; с центром в начале координат?
Расчетная работа №1.
Решение типового примера.
Даны вершины треугольника АВС: А(-4;8), В(5;-4), С(10;6).
Найти:
1) длину стороны АВ;
2) уравнения сторон АВ и АС и их угловые коэффициенты;
3) угол А в радианах;
4) уравнение высоты СD и ее длину;
5) уравнение окружности, для которой высота СD есть диаметр;
6) систему линейных неравенств, определяющих треугольник АВС.
Решение.
1. Найдем длину стороны АВ.
Расстояние d между точками М1(х 1; у 1) и М2(х 2; у 2) определяется по формуле:
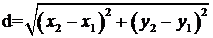 (1)
(1)
Подставив в эту формулу координаты точек А и В, имеем:
АВ= 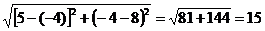
2. Уравнение прямой, проходящей через точки М1(х1; у1) и М2(х2; у2), имеет вид:
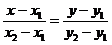 (2)
(2)
Подставив в (2) координаты точек А и В, получим уравнение прямой АВ:
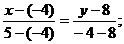

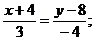
3 у –24 =–4 х –16, 4 х +3 у –8=0 (АВ)
Для нахождения углового коэффициента к АВ прямой АВ, разрешим полученное уравнение относительно у: у = 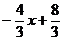 .
.
Отсюда к АВ = 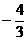 .
.
Подставив в формулу (2) координаты точек А и С, найдем уравнение прямой АС:
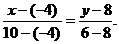
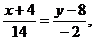
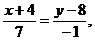
х +7 у –52=0 (АС).
Отсюда к АС = 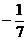 .
.
3. Угол 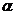 между двумя прямыми, угловые коэффициенты которых равны к 1 и к 2, определяется по формуле:
между двумя прямыми, угловые коэффициенты которых равны к 1 и к 2, определяется по формуле:
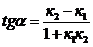 (3)
(3)
Угол А, образованный прямыми АВ и АС, найдем по формуле (3), подставив в нее к 1 = к АВ = 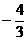 , к 1 = к АС =
, к 1 = к АС = 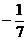 .
.
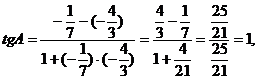
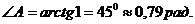
4. Так как высота СD перпендикулярна стороне АВ, то угловые коэффициенты этих прямых обратны по величине и противоположны по знаку, т.е.
к СD = 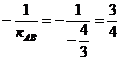 .
.
Уравнение прямой, проходящей через данную точку М1(х1; у1) в заданном направлении, имеет вид:
 (4)
(4)
Подставив в (4) координаты точки С(10;6) и к СD = 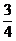 , получим уравнение высоты СD:
, получим уравнение высоты СD:
у – 6 = 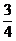 (х – 10), 4 у – 24 = 3 х – 30, 3 х – 4 у – 6 = 0 (СD). (5)
(х – 10), 4 у – 24 = 3 х – 30, 3 х – 4 у – 6 = 0 (СD). (5)
Для нахождения длины СD определим координаты точки D, решив систему уравнений (АВ) и (CD):
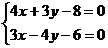 , откуда х = 2, у = 0, то есть D (2; 0)
, откуда х = 2, у = 0, то есть D (2; 0)
Подставив в формулу (1) координаты точек С и D, находим:
СD = 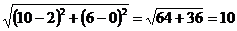 .
.
5. Уравнение окружности радиуса R с центром в точка Е(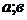 ) имеет вид:
) имеет вид:
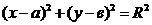 (6)
(6)
Так как СDявляется диаметром искомой окружности, то ее центр Е есть середина отрезка СD. Воспользуемся формулами деления отрезка пополам, получим:
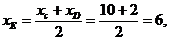
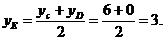
Следовательно, Е(6; 3) и R= 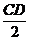 = 5. Используя формулу (6), получаем уравнение искомой окружности:
= 5. Используя формулу (6), получаем уравнение искомой окружности:

6. Множество точек треугольника АВС есть пересечение трех полуплоскостей, первая из которых ограничена прямой АВ и содержит точку С, вторая ограничена прямой ВС и содержит точку А, а третья ограничена прямой АС и содержит точку В.
Для получения неравенства, определяющего полуплоскость, ограниченную прямой АВ и содержащую точку С, подставим в уравнение прямой АВ координаты точки С:
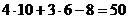 > 0
> 0
Поэтому искомое неравенство имеет вид: 4 х +3 у 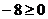 .
.
Для составления неравенства, определяющего полуплоскость, ограниченную прямой ВС и содержащую точку А, найдем уравнение прямой ВС, подставив в формулу (2) координаты точек Ви С:
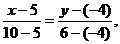
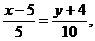
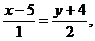
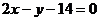 (ВС).
(ВС).
Подставив в последнее уравнение координаты точки А, имеем:
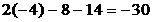 < 0. Искомое неравенство будет 2 х – у – 14
< 0. Искомое неравенство будет 2 х – у – 14 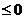 . Подобным образом составим неравенство, определяющее полуплоскость, ограниченную прямой АС и содержащую точку В:
. Подобным образом составим неравенство, определяющее полуплоскость, ограниченную прямой АС и содержащую точку В: 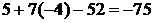 < 0. Третье искомое неравенство будет х +7 у –52
< 0. Третье искомое неравенство будет х +7 у –52 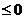 . Итак, множество точек треугольника АВС определяется системой неравенств:
. Итак, множество точек треугольника АВС определяется системой неравенств:
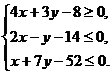
На рис. 1 в декартовой прямоугольной системе координат хОу изображен треугольник АВС, высота СD, окружность с центром в точке Е и диаметром CD
.

Рис. 1



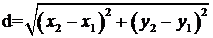 (1)
(1)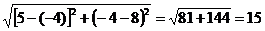
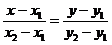 (2)
(2)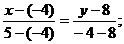

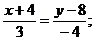
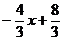 .
.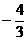 .
.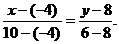
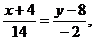
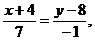
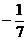 .
.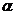 между двумя прямыми, угловые коэффициенты которых равны к 1 и к 2, определяется по формуле:
между двумя прямыми, угловые коэффициенты которых равны к 1 и к 2, определяется по формуле: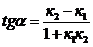 (3)
(3)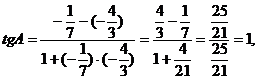
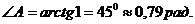
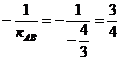 .
. (4)
(4)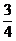 , получим уравнение высоты СD:
, получим уравнение высоты СD: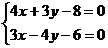 , откуда х = 2, у = 0, то есть D (2; 0)
, откуда х = 2, у = 0, то есть D (2; 0)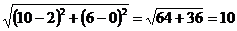 .
.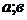 ) имеет вид:
) имеет вид: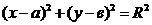 (6)
(6)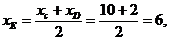
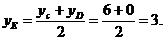
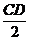 = 5. Используя формулу (6), получаем уравнение искомой окружности:
= 5. Используя формулу (6), получаем уравнение искомой окружности:
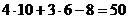 > 0
> 0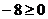 .
.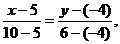
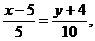
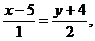
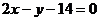 (ВС).
(ВС).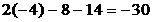 < 0. Искомое неравенство будет 2 х – у – 14
< 0. Искомое неравенство будет 2 х – у – 14 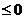 . Подобным образом составим неравенство, определяющее полуплоскость, ограниченную прямой АС и содержащую точку В:
. Подобным образом составим неравенство, определяющее полуплоскость, ограниченную прямой АС и содержащую точку В: 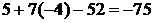 < 0. Третье искомое неравенство будет х +7 у –52
< 0. Третье искомое неравенство будет х +7 у –52 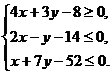

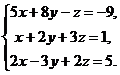 2.
2. 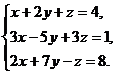
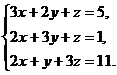 4.
4. 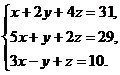
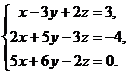 6.
6. 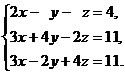
 8.
8. 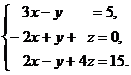
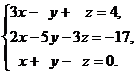 10.
10. 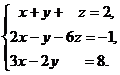
 12.
12. 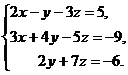
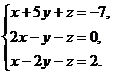 14.
14. 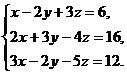
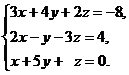 16.
16. 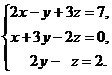
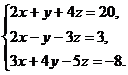 18.
18. 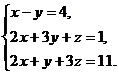
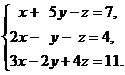 20.
20. 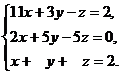
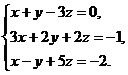 2.
2. 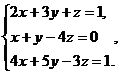
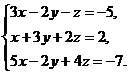 4.
4. 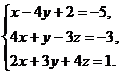
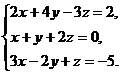 6.
6. 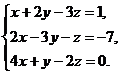
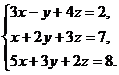 8.
8. 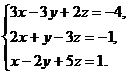
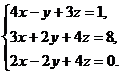 10.
10. 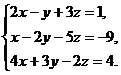
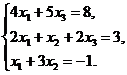 12.
12. 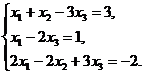
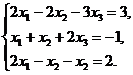 14.
14. 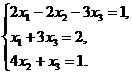
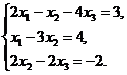 16.
16. 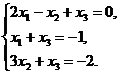
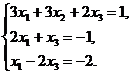 18.
18. 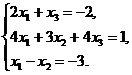
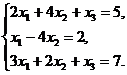 20.
20. 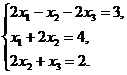
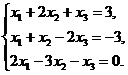 2.
2. 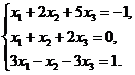
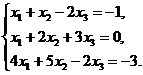 4.
4. 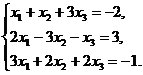
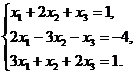 6.
6. 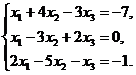
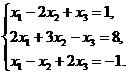 8.
8. 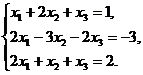
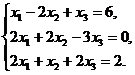 10.
10. 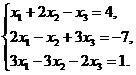
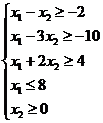 (1)
(1)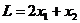 (2)
(2)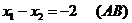 4)
4) 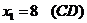
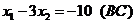 5)
5) 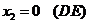
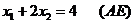

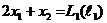 , которая перпендикулярна вектору
, которая перпендикулярна вектору 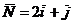 . Если прямую
. Если прямую 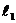 передвигать параллельно самой себе в положительном направлении вектора
передвигать параллельно самой себе в положительном направлении вектора 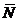 , то линейная форма L будет возрастать, а в противоположном направлении – убывать. Построим прямую
, то линейная форма L будет возрастать, а в противоположном направлении – убывать. Построим прямую 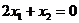 . Как видно из рис. 2, при передвижении прямой
. Как видно из рис. 2, при передвижении прямой 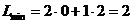 .
. .
.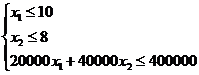 или
или 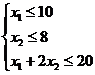 (1)
(1)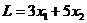 (2)
(2)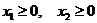 . Решим задачу графическим методом, который был использован при решении задачи 1. Построим многоугольник АВСDЕ (рис. 3), все точки которого удовлетворяют системе неравенств.
. Решим задачу графическим методом, который был использован при решении задачи 1. Построим многоугольник АВСDЕ (рис. 3), все точки которого удовлетворяют системе неравенств.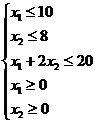 (3)
(3)

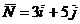 и прямую
и прямую 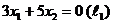 . Перемещая прямую
. Перемещая прямую 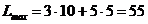 )
)


