Эти две задачи иллюстрируют полезность скалярного произведения.
Сначала рассмотрим, как провести плоскость, проходящую перпендикулярно данному вектору. Вектор единичной длины, перпендикулярный к прямой или плоскости, называется нормальным вектором. Для двумерного случая он имеет вид: n ={cosϑ, sinϑ}. Требуется провести прямую, перпендикулярную этому вектору, и проходящую через точку, лежащую на расстоянии d от начала координат. Рассмотрим вектор r= {x,y}, чей конец бегает по искомой прямой. Проекция вектора r на вектор n всегда должна равна d, значит rn =d.
Записывая скалярное произведение через координаты, получим уравнение прямой, которое называется нормированным: xcosϑ+ysinϑ=d.
Совершенно аналогично запишется и нормированное уравнение для плоскости. Однако нормальный вектор будет иметь вид: n ={ cosα, cosβ, cosγ }, где α, β, γ углы, которые нормальный вектор образует с осями. Здесь конец вектора r бегает по всей искомой плоскости, которая расположена на расстоянии d от начала координат. Уравнение этой плоскости имеет вид:
xcosα +ycosβ+zcosγ=d.
Решение систем уравнений
Часто практические потребности заставляют нас решать системы линейных уравнений, состоящие из числа, гораздо большего, чем три уравнения. Например, в экономике. Однако геометрическое представление полезно и в таком случае, так как основные свойства систем, пояснённые геометрически, часто весьма нехитрым способом переносятся и на случай N уравнений.
Формулы (6) и (8) задают систему линейных уравнений 2-го порядка (2 неизвестных)
Формула (12) задаёт систему линейных уравнений 3-го порядка (3 неизвестных).
Решения системы – набор чисел, подставив которые вместо неизвестных получаем тождества сразу для всех уравнений.
Линейные системы чаще всего решают методом последовательного исключения неизвестных. Например, из формул (6) получим:
 .
.
Подставив это выражение во 2-е уравнение системы (6), получим одно уравнение с одним неизвестным, которое решаем как обычно.
Таким же манером решаем и любую систему N уравнений с N неизвестными.
В итоге неизвестные выразятся через матрицу известных коэффициентов 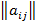 и вектор –столбец известных свободных членов
и вектор –столбец известных свободных членов  .
.
Когда хотя бы один из свободных членов отличен от нуля, система называется неоднородной, когда все они равны нулю – она однородная.
Решение называется тривиальным, когда все «иксы» равны нулю. И напротив, нетривиальным, если хотя бы один из них отличен от нуля.
Когда переменных много, решение получается громоздким. Чтобы не повторять каждый раз одни и те же выкладки, существуют правила Крамера. Они используют понятие определителя (детерминанта).
Детерминант – это число, получаемое из квадратной (N×N) матрицы по определённому алгоритму. Определитель существует для матрицы любого порядка. Для начала приведём формулы для определителей 2-го и 3-го порядков.
Определитель матрицы (7) имеет вид:  . (14)
. (14)
Определитель для матрицы системы (12) имеет вид:
 (15)
(15)
В определителе 5-го порядка таких слагаемых будет уже 120. Поэтому определители порядка выше 3-го в общем виде никогда на выписывают.
Как рассчитать определитель любого порядка?
На практике достаточно знать, как свести определители высокого порядка к определителям 2-го и 3-го порядка. Ответ на этот вопрос даёт теорема Лапласа о дополнительных минорах (адъюнктах).
Минор – это «младший» определитель. Он образуется из исходного определителя вычеркиванием какой-то строки и какого-то столбца. Всего у определителя N порядка N2 миноров.
Матрицу обычно записывают как таблицу в круглых скобках, а определитель – как таблицу в прямых скобках.
Учитывая это, запишем правила Крамера для системы (12):
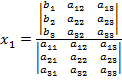

 (*)
(*)
В знаменателе стоит определитель из элементов матрицы, называемый определителем системы.
Ввиду важности этих правил обозначим их звездочкой.
Напоминаем, что каждый определитель – это число, рассчитанное по определённому алгоритму. Поэтому в формуле (*) и числители, и знаменатели – числа.
Теорема Лапласа о дополнительных минорах позволяет последовательно, шаг за шагом, понижать порядок вычисляемого определителя разложением его по строке или по столбцу. В итоге определитель высокого порядка выражается через определители порядка не более 3-его, затем используются формулы (14) и (15).
Поясним примером с определителем 4-го порядка.

Здесь для разложения берём первую строку. Для  дополнительным минором будет определитель 3-го порядка, полученный вычеркиванием строки и столбца, в котором стоит
дополнительным минором будет определитель 3-го порядка, полученный вычеркиванием строки и столбца, в котором стоит  . Помножаем этот определитель на (-1) i+j
. Помножаем этот определитель на (-1) i+j  , то есть, в данном случае просто на
, то есть, в данном случае просто на  .
.
Дополнительный минор для  получается аналогично, но помножать его надо на
получается аналогично, но помножать его надо на  .
.
И далее из одного определителя 4-го порядка получаем 4 определителя 3-го порядка.
Ясно, что решение систем выше 3-го порядка вручную весьма трудоёмкое занятие.
Однако решение систем уравнений 4-го,5-го, 6-го и более высоких порядков давным- давно запрограммировано и совершается на компьютерах за доли секунды.
Подсчёт определителей высокого порядка тоже имеет большое практическое значение. Ибо чтобы неоднородная система имела решение, необходимо, чтобы её определитель был не равен нулю. Подсчет определителя любого порядка меньше 20 занимает на компьютере доли секунды.
Лауреат Нобелевской премии по экономике Василий Васильевич Леонтьев, составляя экономически модели для подъёма экономики Дании, Норвегии и Японии после 2-й мировой войны, обходился моделями из примерно 30 линейных уравнений. В наши дни такие модели легко просчитываются на любом персональном компьютере.
Теперь рассмотрим однородные системы. Начнём с системы 2-го порядка. Две прямые, ей соответствующие, пересекаются в точке{0,0}или же совпадают. Далее перейдём к системе 3-го порядка. Три плоскости пересекаются в точке {0,0,0}, или все три совпадают, проходя через {0,0,0}, или две совпадают, а третья их пересекает, однако они всё равно проходят через точку {0,0,0}. Однако, когда наличествует полное или частичное совпадение, всем трём уравнениям одновременно удовлетворяет не единственная точка {0,0,0}, а все точки прямой проходящей через эту точку, или даже все точки плоскости, которая образовалась после слияния трёх плоскостей.
В общем случае об однородных системах линейных уравнений доказана теорема:



 .
.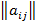 и вектор –столбец известных свободных членов
и вектор –столбец известных свободных членов  .
. . (14)
. (14) (15)
(15)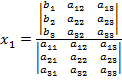

 (*)
(*)
 дополнительным минором будет определитель 3-го порядка, полученный вычеркиванием строки и столбца, в котором стоит
дополнительным минором будет определитель 3-го порядка, полученный вычеркиванием строки и столбца, в котором стоит  , то есть, в данном случае просто на
, то есть, в данном случае просто на  получается аналогично, но помножать его надо на
получается аналогично, но помножать его надо на  .
.