1. Строят прямые, соответствующие стратегиям второго (первого) игрока.
2. Находят две стратегии второго (первого) игрока, которым соответствуют две прямые, пересекающиеся в точке с максимальной (минимальной) ординатой. Эти стратегии являются активными в оптимальной смешанной стратегии второго (первого) игрока.
3. Находят координаты точки пересечения, тем самым определяя оптимальную стратегию первого (второго) игрока и цену игры.
4. Оптимальную стратегию другого игрока находят, решая систему уравнений, включающую его активные стратегии.
Пример 5.4. Найдите решение игры, заданной матрицей:
| A =
| 
| 7 9 8 10 6 9
|  . .
|
Решение.
 Сначала проверим наличие седловой точки:
Сначала проверим наличие седловой точки:  = 7,
= 7,  = 9. Поскольку нижняя и верхняя цены игры не совпадают, седловая точка отсутствует, и решение следует искать в смешанных стратегиях.
= 9. Поскольку нижняя и верхняя цены игры не совпадают, седловая точка отсутствует, и решение следует искать в смешанных стратегиях.
Выполним построения на плоскости XY в соответствии с методикой, приведенной выше. Результат представлен на рисунке 5.3.
Рисунок 5.3 – Геометрическая интерпретация игры примера 5.4
Точка М находится на пересечении отрезков, соответствующих стратегиям B1 и B2 второго игрока.
Найдем ее координаты:
B1B'1:
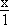 = =  , откуда y = 3x + 7, , откуда y = 3x + 7,
|
B2B'2:
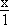 = =  , откуда y = -3x + 9, , откуда y = -3x + 9,
|
|
| 3x + 7 = -3x + 9, 6x = 2, x = 1/3, т.е. 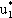 = 2/3, = 2/3, 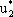 = 1/3, цена игры v = 8. = 1/3, цена игры v = 8.
|
Активными стратегиями игрока B являются стратегии B1 и B2, следовательно,  = 0.
= 0.
Используя выражение (5.2), вытекающее из теоремы об активных стратегиях, составим систему из двух уравнений с двумя неизвестными:
Второе уравнение умножим на семь и вычтем из первого:
Ответ: U* = (2/3, 1/3); Z* = (1/2, 1/2, 0); v = 8.
Пример 5.5. Найдите решение игры, заданной матрицей:
| A =
| 
| 6 5 4 6 2 7 1 8
| 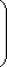 . .
|
Решение.
Проверим наличие седловой точки.
|
|  = max (5, 4, 2, 1) = 5, = max (5, 4, 2, 1) = 5,  = min (6, 8) = 6. = min (6, 8) = 6.
|
 Седловая точка отсутствует, поэтому решение следует искать в смешанных стратегиях.
Седловая точка отсутствует, поэтому решение следует искать в смешанных стратегиях.
Выполним построения на плоскости XY в соответствии с методикой, приведенной выше. Результат представлен на рисунке 5.4.
Рисунок 5.4 – Геометрическая интерпретация игры примера 5.5
В данном случае необходимо отыскать точку, соответствующую минимальному гарантированному проигрышу. Такая точка (точка М) находится на пересечении отрезков, соответствующих стратегиям А1 и А4 игрока А.
Найдем координаты:
A1A'1:
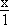 = =  , откуда y = -x + 6, , откуда y = -x + 6,
|
A4A'4:
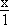 = =  , откуда y = 7x + 1, , откуда y = 7x + 1,
|
|
| 7x + 1 = -x + 6, 8x = 5, x = 5/8, 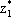 = 3/8, = 3/8, 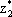 = 5/8, v = 43/8. = 5/8, v = 43/8.
|
Активными стратегиями игрока A являются стратегии A1 и A4, следовательно, 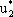 =
=  = 0.
= 0.
Используя выражение (5.1), вытекающее из теоремы об активных стратегиях, составим систему из двух уравнений с двумя неизвестными:
Вычтем из первого уравнения второе:
Ответ: U* = (7/8, 0, 0, 1/8); Z* = (3/8, 5/8); v = 43/8.
21.Доминирование смешанных стратегий для игрока A.
Один из способов упрощения игр основывается на принципе доминирования, который позволяет в некоторых случаях игру с матрицей А свести к эквивалентной игре с матрицей меньшего размера.
А=
Между множеством 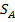 смешанных (в том числе и чистых) стратегий
смешанных (в том числе и чистых) стратегий  игрока А и выпуклыми комбинациями
игрока А и выпуклыми комбинациями

строк ( матрицы А, представляющими собой строки
матрицы А, представляющими собой строки  выигрышей
выигрышей  , j=1,2,…,n, игрока А в ситуациях
, j=1,2,…,n, игрока А в ситуациях  , j=1,2,…,n, устанавливается взаимно-однозначное соответствие
, j=1,2,…,n, устанавливается взаимно-однозначное соответствие

из которого ясно, что, в частности, каждой чистой стратегии  игрока А ставится во взаимно-однозначное соответствие k-я строка
игрока А ставится во взаимно-однозначное соответствие k-я строка 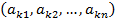 матрицы А.
матрицы А.
Если для двух выпуклых комбинаций строк матрицы А

и

выполняются неравенства

то говорят, что строка (2) доминирует строку (1), а строка (1) доминирует строкой (2). Если каждое неравенство (3) является равенством, то строки (1) и (2) называют дублирующими. Если же каждое неравенство (3) является строгим, то говорят, что строка (2) строго доминирует строку (1), а строка (1) строго доминируется строкой (2).
Аналогичная терминология используется и для соответствующих стратегий игрока А. А именно, если строка (2) доминирует, соответственно дублирует, соответственно строго доминирует строку (1), то говорят, что стратегия  доминирует, соответственно дублирует, соответственно строго доминирует стратегию
доминирует, соответственно дублирует, соответственно строго доминирует стратегию 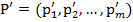 .
.
Таким образом, по данным определениям и для игрока А, предпочтительными оказываются доминирующие стратегии.
22.Доминирование смешанных стратегий для игрока B.
Один из способов упрощения игр основывается на принципе доминирования, который позволяет в некоторых случаях игру с матрицей А свести к эквивалентной игре с матрицей меньшего размера.
А=
Между смешанными (в том числе и чистыми) стратегиями  игрока В и выпуклыми комбинациями
игрока В и выпуклыми комбинациями
 T,
T, 
столбцов  T, j=1,2,…,n, матрицы А (Т- значок транспонирования), представляющими собой столбцы
T, j=1,2,…,n, матрицы А (Т- значок транспонирования), представляющими собой столбцы 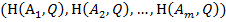 T
T
проигрышей Н(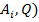 , i=1,2,…,m, игрока В в ситуациях (
, i=1,2,…,m, игрока В в ситуациях (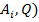 , i=1,2,…,m, устанавливается взаимно-однозначное соответствие
, i=1,2,…,m, устанавливается взаимно-однозначное соответствие
 T ,
T ,
из которого видно, что, в частности, каждой чистой стратегии  , l =1,2,…,n, игрока В ставится во взаимно-однозначное соответствие l -й столбец
, l =1,2,…,n, игрока В ставится во взаимно-однозначное соответствие l -й столбец  T матрицы А.
T матрицы А.
Если для двух выпуклых комбинаций столбцов матрицы А
 T
T 
и
 T
T 
выполняются неравенства

то говорят, что столбец (4) (стратегия 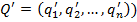 доминирует столбец (5) (стратегию
доминирует столбец (5) (стратегию  , а столбец (5) (стратегия
, а столбец (5) (стратегия  ) доминируется столбцом (4) (стратегией
) доминируется столбцом (4) (стратегией  ). Если каждое неравенство (6) является равенством, то столбцы (4) и (5) (стратегии
). Если каждое неравенство (6) является равенством, то столбцы (4) и (5) (стратегии  и
и  ) называют дублирующими друг друга. Если же каждое неравенство (6) является строгим, то говорят, что столбец (4) (стратегия
) называют дублирующими друг друга. Если же каждое неравенство (6) является строгим, то говорят, что столбец (4) (стратегия  ) строго доминирует столбец (5) (стратегию
) строго доминирует столбец (5) (стратегию  ), а столбец (5) (стратегия
), а столбец (5) (стратегия  ) строго доминируется столбцом (4) (стратегией
) строго доминируется столбцом (4) (стратегией  ).
).
Таким образом, по данным определениям для игрока В предпочтительными оказываются доминирующие стратегии.
23. Решение матричной игры m × n сведением к задаче линейного программирования для игрока A.
Пусть дана матричная игра с матрицей А порядка m х n.
А=
Po=(p1o,p2o,…,pmo)
 ,
,
Если игрок А применяет любую смешанную стратегию P=(p1,p2,…,pm) против любой чистой стратегии Bj игрока В, то он получает выигрыш
F(P,Bj)=a1jp1+a2jp2+…+anjpm, j=1,2,…,n
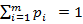 .
.

Разделим каждое неравенство на V>0 и введем
x1=p1/v, x2=p2/v,…,xm=pm/v
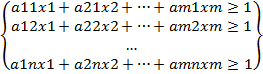
Разделив на V>0 равенство 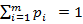 , получим выражение x1+x2+…+xm=1/v
, получим выражение x1+x2+…+xm=1/v
Получаем задачу линейного программирования для игрока А:
x1+x2+…+xm->min(поскольку первый игрок стремится найти такие значения хi и, следовательно, pi, чтобы цена игры v была максимальной)
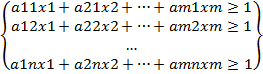
Po=(p1o=x1o*V, p2o=x2o*V,…,pmo=xmo*V)
24. Решение матричной игры m × n сведением к задаче линейного программирования для игрока B.
Пусть дана матричная игра с матрицей А порядка m х n.
А=
Qo=(q1o,q2o,…,qno)

Если игрок В применяет любую смешанную стратегию Q=(q1,q2,…,qm) против любой чистой стратегии Ai игрока A, то он получает проигрыш
F(P,Bj)=a1jq1+a2jq2+…+anjqm, j=1,2,…,n
 .
.

Разделим каждое неравенство на V>0 и введем
y1=q1/v, y2=q2/v,…,ym=qm/v

Разделив на V>0 равенство  , получим выражение y1+y2+…+ym=1/v
, получим выражение y1+y2+…+ym=1/v
Получаем задачу линейного программирования для игрока В:
y1+y2+…+ym->max (поскольку второй игрок стремится найти такие значения yj и, следовательно, qj, чтобы цена игры v была наименьшей)

Qo=(q1o=y1o*V, q2o=y2o*V,…,qmo=ymo*V)
25. Основные понятия и определения теории игр с природой.
Во многих задачах финансово-экономической сферы принятие решения осложняется наличием неопределенности, заключающейся в неполноте информации об окружающей среде. Такую неопределенность могут порождать различные причины. Это могут быть действительные природные физические (климатические), биологические, химические, социальные и другие процессы, которые сопровождают экономическую деятельность, политика гос-ва и др. Поэтому в таких задачах принятие решения зависит от реальных условий, которые называют в соответствующей математической модели «природой». Саму же модель называют «игрой с природой». «Природа» может выступать как антагонистическая сторона, а может как кооперативная среда. Игру с природой можно определить как парную игру, в которой сознательный игрок А, заинтересованный в наиболее выгодном для него исходе игры, выступает против участника, совершенно безразличного к результату – природа (обозначим его П). Очевидно, что при решении игр с природой достаточно найти наилучшие рекомендации только для игрока А, потому как природа в рекомендациях не нуждается, развиваясь в соответствии с определенными законами независимо от того, удобно это человеку или нет.




 .
.
 Сначала проверим наличие седловой точки:
Сначала проверим наличие седловой точки:  = 7,
= 7,  = 9. Поскольку нижняя и верхняя цены игры не совпадают, седловая точка отсутствует, и решение следует искать в смешанных стратегиях.
= 9. Поскольку нижняя и верхняя цены игры не совпадают, седловая точка отсутствует, и решение следует искать в смешанных стратегиях.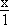 =
=  , откуда y = 3x + 7,
, откуда y = 3x + 7,
 , откуда y = -3x + 9,
, откуда y = -3x + 9,
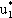 = 2/3,
= 2/3, 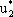 = 1/3, цена игры v = 8.
= 1/3, цена игры v = 8.
 = 0.
= 0.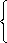
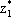 + 9
+ 9 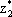 = 8,
= 8, 
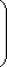 .
.
 Седловая точка отсутствует, поэтому решение следует искать в смешанных стратегиях.
Седловая точка отсутствует, поэтому решение следует искать в смешанных стратегиях. , откуда y = -x + 6,
, откуда y = -x + 6,
 , откуда y = 7x + 1,
, откуда y = 7x + 1,
 = 0.
= 0.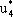 = 43/8,
= 43/8, 




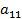

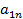


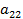



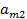

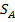 смешанных (в том числе и чистых) стратегий
смешанных (в том числе и чистых) стратегий  игрока А и выпуклыми комбинациями
игрока А и выпуклыми комбинациями
 матрицы А, представляющими собой строки
матрицы А, представляющими собой строки  выигрышей
выигрышей  , j=1,2,…,n, игрока А в ситуациях
, j=1,2,…,n, игрока А в ситуациях  , j=1,2,…,n, устанавливается взаимно-однозначное соответствие
, j=1,2,…,n, устанавливается взаимно-однозначное соответствие
 игрока А ставится во взаимно-однозначное соответствие k-я строка
игрока А ставится во взаимно-однозначное соответствие k-я строка 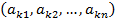 матрицы А.
матрицы А.


 доминирует, соответственно дублирует, соответственно строго доминирует стратегию
доминирует, соответственно дублирует, соответственно строго доминирует стратегию 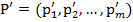 .
. игрока В и выпуклыми комбинациями
игрока В и выпуклыми комбинациями T,
T, 
 T, j=1,2,…,n, матрицы А (Т- значок транспонирования), представляющими собой столбцы
T, j=1,2,…,n, матрицы А (Т- значок транспонирования), представляющими собой столбцы 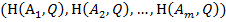 T
T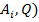 , i=1,2,…,m, игрока В в ситуациях (
, i=1,2,…,m, игрока В в ситуациях ( T ,
T , , l =1,2,…,n, игрока В ставится во взаимно-однозначное соответствие l -й столбец
, l =1,2,…,n, игрока В ставится во взаимно-однозначное соответствие l -й столбец  T матрицы А.
T матрицы А. T
T 
 T
T 

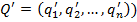 доминирует столбец (5) (стратегию
доминирует столбец (5) (стратегию  , а столбец (5) (стратегия
, а столбец (5) (стратегия  ) доминируется столбцом (4) (стратегией
) доминируется столбцом (4) (стратегией  ). Если каждое неравенство (6) является равенством, то столбцы (4) и (5) (стратегии
). Если каждое неравенство (6) является равенством, то столбцы (4) и (5) (стратегии  ,
,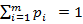 .
.
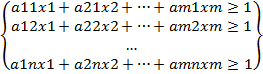

 .
.




