Запишем объединенный закон первого и второго начал термодинамики в виде
 (13.1)
(13.1)
Каждое слагаемое правой части уравнения представляет собой произведение интенсивного параметра на дифференциал экстенсивного параметра. Ни один из этих членов не является полным дифференциалом, в то время как их сумма есть полный дифференциал.
Слагаемое  учитывает изменение внутренней энергии, связанное с приростом намагниченности
учитывает изменение внутренней энергии, связанное с приростом намагниченности  в магнитном поле
в магнитном поле  .
.  - механическая работа,
- механическая работа,  - учитывает изменение химического потенциала.
- учитывает изменение химического потенциала.
Форма записанного уравнения (13.1) говорит о том, что  есть полный дифференциал и, если ее выразить как функцию
есть полный дифференциал и, если ее выразить как функцию  , то она приобретает свойства потенциальной функции.
, то она приобретает свойства потенциальной функции.
 (13.2)
(13.2)
Сравнивая уравнения (13.2) и (13.1) можно сделать вывод о том, что частная производная потенциала по одному из экстенсивных параметров равна соответствующему интенсивному параметру, который тем самым аналогичен некоторой консервативной силе, действительно
 (13.3)
(13.3)
Таким образом, если внутренняя энергия определена как функция экстенсивных параметров, то различные частные производные подставляют нам соответствуют интенсивные параметры. Воспользоваться уравнениями (13.3), но если проинтегрировать выражение (13.1).
Внутренняя энергия  экстенсивная функция для интегрирования ее зависимости воспользуемся приемом предложенном Эйлером. При изменении количества в
экстенсивная функция для интегрирования ее зависимости воспользуемся приемом предложенном Эйлером. При изменении количества в  раз во столько же раз изменится и величина всех экстенсивных параметров. Для простоты мы запишем экстенсивные параметры в виде символов
раз во столько же раз изменится и величина всех экстенсивных параметров. Для простоты мы запишем экстенсивные параметры в виде символов  а интенсивные через
а интенсивные через 
 .
.
Продифференцируем уравнения  (13.1) и (13.2) по
(13.1) и (13.2) по 
 ;
;
 .
.
Осуществив обратную рокировку записи переменных, придем к выражению
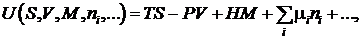 (13.4)
(13.4)
известному как уравнение Эйлера, в котором все интенсивные параметры выражены явно через экстенсивные параметры системы. Т.е. могут быть вычислены из выражения (13.4) путем математических преобразований и дифференцирования.
Продифференцируем уравнение Эйлера
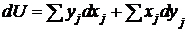
и вычтем из него первоначально записанный дифференциал  приходим к выводу, что
приходим к выводу, что  , т.е.
, т.е.
 .
.
В частности для однокомпонентного вещества в количестве 1 моль (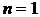 ) получим
) получим
 ,
,
где  и т.д. – значения энтропии, объема, намагничивания и т.д. на 1 моль вещества (например,
и т.д. – значения энтропии, объема, намагничивания и т.д. на 1 моль вещества (например,  , где
, где  - молярная масса вещества, а
- молярная масса вещества, а  - его плотность).
- его плотность).
При поиске теплофизических свойств веществ часто отправной точкой служит уравнение для полного дифференциала внутренней энергии.
Внутренняя энергия есть потенциал функции
 , (13.5)
, (13.5)
где равенство справедливо для обратимых процессов, неравенство – для необратимых.
Если все параметры экстенсивные поддерживаются постоянными (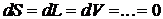 ) пока система самопроизвольно приходит в состояние равновесия, то всякое изменение внутренней энергии сводится к ее уменьшению.
) пока система самопроизвольно приходит в состояние равновесия, то всякое изменение внутренней энергии сводится к ее уменьшению.
Самопроизвольное изменение прекратится в том случае, когда дальнейшее снижение станет невозможным. Таким образом, при равновесии величина внутренней энергии  – минимальна. В том случае, когда экстенсивные параметры зафиксированы состояние равновесия это состояние с минимальной величиной
– минимальна. В том случае, когда экстенсивные параметры зафиксированы состояние равновесия это состояние с минимальной величиной  .
.
Если организовать адиабатное протекание процесса  (и поддерживать
(и поддерживать  ), то внутренняя энергия в течении процесса остается неизменной, а
), то внутренняя энергия в течении процесса остается неизменной, а 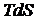 удовлетворяет условию
удовлетворяет условию  , следовательно при равновесии энтропия достигает своего максимального значения. Если бы мы в течении самопроизвольного процесса попытались бы сохранять
, следовательно при равновесии энтропия достигает своего максимального значения. Если бы мы в течении самопроизвольного процесса попытались бы сохранять  , то нам пришлось бы отводить теплоту в количестве, достаточном для того, чтобы скомпенсировать прирост энтропии
, то нам пришлось бы отводить теплоту в количестве, достаточном для того, чтобы скомпенсировать прирост энтропии  , а это снижало бы внутреннюю энергию
, а это снижало бы внутреннюю энергию  до тех пор, пока она не достигла минимальной величины. Если все механические экстенсивные параметры поддерживать неизменными, то подвод тепла ведет к росту внутренней энергии. Воспользовавшись правилом перекрестного дифференцирования и независимостью производной от очередности дифференцирования по переменным к дифференциалу внутренней энергии, получим ряд соотношений, которые в термодинамике принято называть уравнениями Максвелла
до тех пор, пока она не достигла минимальной величины. Если все механические экстенсивные параметры поддерживать неизменными, то подвод тепла ведет к росту внутренней энергии. Воспользовавшись правилом перекрестного дифференцирования и независимостью производной от очередности дифференцирования по переменным к дифференциалу внутренней энергии, получим ряд соотношений, которые в термодинамике принято называть уравнениями Максвелла
 , (13.6)
, (13.6)
Выражение 13.6 справедливы для обратимых процессов. Ими пользуются для вычисления разностей различных термодинамических параметров между двумя состояниями равновесия.
Энтальпия
Энтальпия, как термодинамический потенциал в случае, когда независимыми переменными являются параметры Р и Т, выглядит более предпочтительно. Температуру проще измерять, чем энтропию. Часто в процессах проще поддерживать постоянным объем, а не давление.
Запишем выражение для энтальпии
 ,
,
тогда ее дифференциал может быть представлен в виде
 (13.7)
(13.7)
Если состояние системы поддерживать при ( ,
, 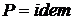 ,
,  ), то энтальпия при равновесном состоянии будет минимальной. Частные производные энтальпии I имеет вид
), то энтальпия при равновесном состоянии будет минимальной. Частные производные энтальпии I имеет вид
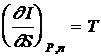 ;
;  ;
; 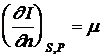 .
.
Соответствующие уравнения Максвелла могут быть сведены к виду
 ;
;  ;
;  .
.
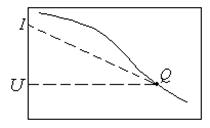 Рисунок 13.1
Преобразования Лежандра с переходом от
Рисунок 13.1
Преобразования Лежандра с переходом от  как функции как функции  к к 
|
Геометрически переход от  к I есть пример преобразования Лежандра для пары двух переменных P и V. Функция
к I есть пример преобразования Лежандра для пары двух переменных P и V. Функция  (V) при заданном значении V (в точке Q) имеет наклон
(V) при заданном значении V (в точке Q) имеет наклон  , который определяет угловой коэффициент касательной
, который определяет угловой коэффициент касательной  , пересекающей ось
, пересекающей ось  в точке
в точке  . Решив уравнение
. Решив уравнение 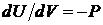 относительно V как функции Р, можно I выразить как функцию наклона касательной, равного
относительно V как функции Р, можно I выразить как функцию наклона касательной, равного  . Таким образом энтальпию можно рассматривать как потенциальную функцию, в которой вместо независимой переменной V используется независимая переменная Р.
. Таким образом энтальпию можно рассматривать как потенциальную функцию, в которой вместо независимой переменной V используется независимая переменная Р.
Функция Гельмгольца
Заменим независимую переменную  параметром
параметром  . Адиабатные процессы (
. Адиабатные процессы ( ) достаточно распространены в природе, но не менее важное значение имеют изотермические процессы, ибо многие термодинамические измерения осуществляют при постоянной температуре. Используя соответствующее преобразование Лежандра, получим функцию Гельмгольца
) достаточно распространены в природе, но не менее важное значение имеют изотермические процессы, ибо многие термодинамические измерения осуществляют при постоянной температуре. Используя соответствующее преобразование Лежандра, получим функцию Гельмгольца  , для которой
, для которой
 , (13.8)
, (13.8)
где  ; и т.д.
; и т.д.
Уравнения Максвелла в этом случае могут быть записаны в виде
Для этого случая уравнения Максвелла примут вид
 и т.д. (13.9)
и т.д. (13.9)
Поскольку изохорная теплоемкость  , то дифференцирование этих уравнений по
, то дифференцирование этих уравнений по  дает систему
дает систему
 ;
;
 и т.д. (13.10)
и т.д. (13.10)
Как видно, теплоемкость не полностью независима от уравнений состояния. Зависимость  от
от  можно установить непосредственными измерениями, а ее зависимость от других переменных
можно установить непосредственными измерениями, а ее зависимость от других переменных  и т.д. находят из уравнений состояния.
и т.д. находят из уравнений состояния.
Знак неравенства в уравнении для полного дифференциала функции Гельмгольца (свободной энергии) обозначает, что для системы с постоянными параметрами  и т.д. функция Гельмгольца при равновесии приобретает минимальное значение. Если реализовать процесс при
и т.д. функция Гельмгольца при равновесии приобретает минимальное значение. Если реализовать процесс при 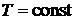 , то всякое изменение
, то всякое изменение  можно полностью преобразовать в такую работу, как
можно полностью преобразовать в такую работу, как  или
или  и т.д. Поэтому функцию
и т.д. Поэтому функцию  часто называют свободной энергией системы при постоянной температуре. Как вытекает из второго уравнения Максвелла, например, поскольку при усилении магнитной поляризации порядок в расположении атомных магнитов становится больше, поскольку энтропия (мера беспорядка) с ростом
часто называют свободной энергией системы при постоянной температуре. Как вытекает из второго уравнения Максвелла, например, поскольку при усилении магнитной поляризации порядок в расположении атомных магнитов становится больше, поскольку энтропия (мера беспорядка) с ростом  убывает. Поэтому напряженность магнитного поля
убывает. Поэтому напряженность магнитного поля  , необходимая для достижения заданной намагниченности
, необходимая для достижения заданной намагниченности  , тем больше, чем выше
, тем больше, чем выше  .
.
Функция Гиббса
Еще одним достаточно важным потенциалом в термодинамике является функция Гиббса
 (13.11)
(13.11)
с естественными координатами  и
и 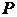 вместо
вместо  и
и  . Ее полный дифференциал может быть записан в виде
. Ее полный дифференциал может быть записан в виде
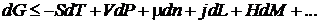
Характерность функции Гиббса подчеркивается частными производными
 ;
; 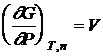 и т.д. (13.12)
и т.д. (13.12)
Как и другие характеристические функции для систем при постоянных значениях функция Гиббса имеет минимальное значение.
Уравнение Максвелла в этом случае запишутся в виде
;  и т.д. (13.13)
и т.д. (13.13)
Функцию Гиббса иногда называют свободной энергией системы при  и
и 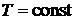 . Она представляет ту работу, которую можно получить при постоянном давлении и постоянной температуре.
. Она представляет ту работу, которую можно получить при постоянном давлении и постоянной температуре.
Этот процесс можно распространить на все механические параметры всякий раз приходя к новому потенциалу и новому ряду уравнений Максвелла.
Например, для магнитной функции Гиббса
 (13.14)
(13.14)
можно записать
 и т.д. (13.15)
и т.д. (13.15)
Можно определить еще и общий потенциал  , который можно вывести, используя преобразования Лежандра, при переходе от независимой переменной
, который можно вывести, используя преобразования Лежандра, при переходе от независимой переменной  к независимому переменному
к независимому переменному  , удобному при изучении систем с переменным числом частиц, как это бывает в квантовых системах
, удобному при изучении систем с переменным числом частиц, как это бывает в квантовых системах
 ,
,
 , (13.16)
, (13.16)
откуда следуют уравнения Максвелла
 и т.д. (13.17)
и т.д. (13.17)



 (13.1)
(13.1) учитывает изменение внутренней энергии, связанное с приростом намагниченности
учитывает изменение внутренней энергии, связанное с приростом намагниченности  в магнитном поле
в магнитном поле  .
.  - механическая работа,
- механическая работа,  - учитывает изменение химического потенциала.
- учитывает изменение химического потенциала. есть полный дифференциал и, если ее выразить как функцию
есть полный дифференциал и, если ее выразить как функцию  , то она приобретает свойства потенциальной функции.
, то она приобретает свойства потенциальной функции. (13.2)
(13.2) (13.3)
(13.3) экстенсивная функция для интегрирования ее зависимости воспользуемся приемом предложенном Эйлером. При изменении количества в
экстенсивная функция для интегрирования ее зависимости воспользуемся приемом предложенном Эйлером. При изменении количества в  раз во столько же раз изменится и величина всех экстенсивных параметров. Для простоты мы запишем экстенсивные параметры в виде символов
раз во столько же раз изменится и величина всех экстенсивных параметров. Для простоты мы запишем экстенсивные параметры в виде символов  а интенсивные через
а интенсивные через 
 .
.
 ;
; .
.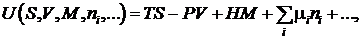 (13.4)
(13.4)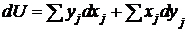
 приходим к выводу, что
приходим к выводу, что  , т.е.
, т.е. .
.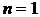 ) получим
) получим ,
, и т.д. – значения энтропии, объема, намагничивания и т.д. на 1 моль вещества (например,
и т.д. – значения энтропии, объема, намагничивания и т.д. на 1 моль вещества (например,  , где
, где  - молярная масса вещества, а
- молярная масса вещества, а  - его плотность).
- его плотность). , (13.5)
, (13.5)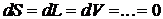 ) пока система самопроизвольно приходит в состояние равновесия, то всякое изменение внутренней энергии сводится к ее уменьшению.
) пока система самопроизвольно приходит в состояние равновесия, то всякое изменение внутренней энергии сводится к ее уменьшению. (и поддерживать
(и поддерживать  ), то внутренняя энергия в течении процесса остается неизменной, а
), то внутренняя энергия в течении процесса остается неизменной, а 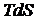 удовлетворяет условию
удовлетворяет условию  , следовательно при равновесии энтропия достигает своего максимального значения. Если бы мы в течении самопроизвольного процесса попытались бы сохранять
, следовательно при равновесии энтропия достигает своего максимального значения. Если бы мы в течении самопроизвольного процесса попытались бы сохранять  , то нам пришлось бы отводить теплоту в количестве, достаточном для того, чтобы скомпенсировать прирост энтропии
, то нам пришлось бы отводить теплоту в количестве, достаточном для того, чтобы скомпенсировать прирост энтропии  , а это снижало бы внутреннюю энергию
, а это снижало бы внутреннюю энергию  до тех пор, пока она не достигла минимальной величины. Если все механические экстенсивные параметры поддерживать неизменными, то подвод тепла ведет к росту внутренней энергии. Воспользовавшись правилом перекрестного дифференцирования и независимостью производной от очередности дифференцирования по переменным к дифференциалу внутренней энергии, получим ряд соотношений, которые в термодинамике принято называть уравнениями Максвелла
до тех пор, пока она не достигла минимальной величины. Если все механические экстенсивные параметры поддерживать неизменными, то подвод тепла ведет к росту внутренней энергии. Воспользовавшись правилом перекрестного дифференцирования и независимостью производной от очередности дифференцирования по переменным к дифференциалу внутренней энергии, получим ряд соотношений, которые в термодинамике принято называть уравнениями Максвелла , (13.6)
, (13.6) ,
, (13.7)
(13.7) ,
, 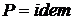 ,
,  ), то энтальпия при равновесном состоянии будет минимальной. Частные производные энтальпии I имеет вид
), то энтальпия при равновесном состоянии будет минимальной. Частные производные энтальпии I имеет вид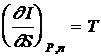 ;
;  ;
; 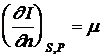 .
. ;
;  ;
;  .
. Рисунок 13.1
Преобразования Лежандра с переходом от
Рисунок 13.1
Преобразования Лежандра с переходом от  к
к 
 , который определяет угловой коэффициент касательной
, который определяет угловой коэффициент касательной  , пересекающей ось
, пересекающей ось 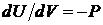 относительно V как функции Р, можно I выразить как функцию наклона касательной, равного
относительно V как функции Р, можно I выразить как функцию наклона касательной, равного  . Таким образом энтальпию можно рассматривать как потенциальную функцию, в которой вместо независимой переменной V используется независимая переменная Р.
. Таким образом энтальпию можно рассматривать как потенциальную функцию, в которой вместо независимой переменной V используется независимая переменная Р. . Адиабатные процессы (
. Адиабатные процессы ( , для которой
, для которой , (13.8)
, (13.8) ; и т.д.
; и т.д. и т.д. (13.9)
и т.д. (13.9) , то дифференцирование этих уравнений по
, то дифференцирование этих уравнений по  ;
; и т.д. (13.10)
и т.д. (13.10) от
от  и т.д. находят из уравнений состояния.
и т.д. находят из уравнений состояния. и т.д. функция Гельмгольца при равновесии приобретает минимальное значение. Если реализовать процесс при
и т.д. функция Гельмгольца при равновесии приобретает минимальное значение. Если реализовать процесс при 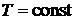 , то всякое изменение
, то всякое изменение  можно полностью преобразовать в такую работу, как
можно полностью преобразовать в такую работу, как  или
или  и т.д. Поэтому функцию
и т.д. Поэтому функцию  убывает. Поэтому напряженность магнитного поля
убывает. Поэтому напряженность магнитного поля  , необходимая для достижения заданной намагниченности
, необходимая для достижения заданной намагниченности  (13.11)
(13.11)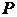 вместо
вместо  . Ее полный дифференциал может быть записан в виде
. Ее полный дифференциал может быть записан в виде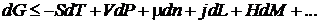
 ;
; 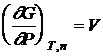 и т.д. (13.12)
и т.д. (13.12) и т.д. (13.13)
и т.д. (13.13) и
и  (13.14)
(13.14) и т.д. (13.15)
и т.д. (13.15) , который можно вывести, используя преобразования Лежандра, при переходе от независимой переменной
, который можно вывести, используя преобразования Лежандра, при переходе от независимой переменной  к независимому переменному
к независимому переменному  ,
, , (13.16)
, (13.16) и т.д. (13.17)
и т.д. (13.17)


