Рассмотрим в пространстве прямоугольную систему координат Oxyz. Выделим на координатных осях Ox, Oy и Oz единичные векторы (орты), обозначаемые 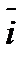 ,
, 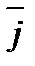 ,
, 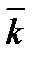 соответственно (см. рис 12).
соответственно (см. рис 12).
Выберем произвольный вектор 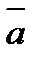 пространства и совместим его начало с началом координат:
пространства и совместим его начало с началом координат: 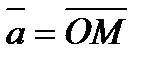 .
.
Найдем проекции вектора 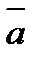 на координатные оси. Проведем через конец вектора
на координатные оси. Проведем через конец вектора 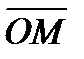 плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с координатными осями обозначим соответственно через M 1, М 2 и М 3. Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор
плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с координатными осями обозначим соответственно через M 1, М 2 и М 3. Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор 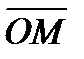 . Тогда пр х
. Тогда пр х 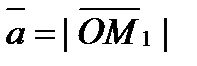 , пр y
, пр y 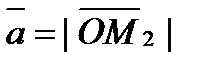 , пр z
, пр z 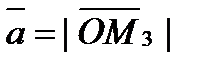 . По определению суммы нескольких векторов находим
. По определению суммы нескольких векторов находим 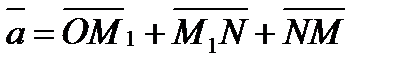
А так как 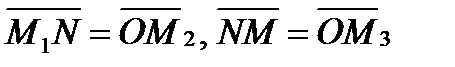 , то
, то
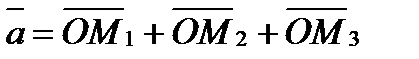 (5.1)
(5.1)
Но 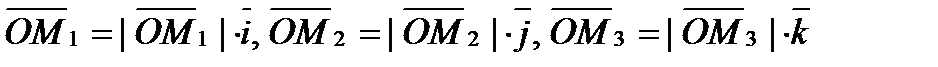 (5.2)
(5.2)
Обозначим проекции вектора 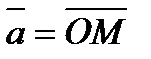 на оси Ox, Oy и Oz соответственно через
на оси Ox, Oy и Oz соответственно через 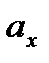 ,
, 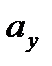 и
и 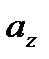 , т.е.
, т.е. 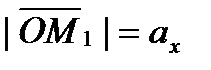 ,
, 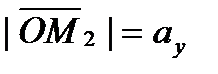 ,
, 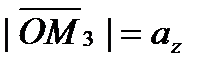 . Тогда из равенств (5.1) и (5.2) получаем
. Тогда из равенств (5.1) и (5.2) получаем
Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа 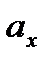 ,
, 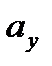 ,
, 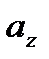 называются координатами вектора
называются координатами вектора 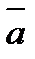 , т.е. координаты вектора есть его проекции на соответствующие координатные оси.
, т.е. координаты вектора есть его проекции на соответствующие координатные оси.
Векторное равенство (5.3) часто записывают в символическом виде: 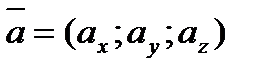 .
.
Равенство 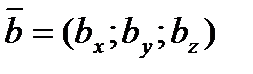 означает, что
означает, что 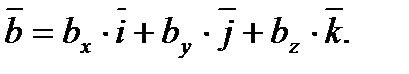
Зная проекции вектора 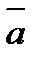 , можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно написать
, можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно написать 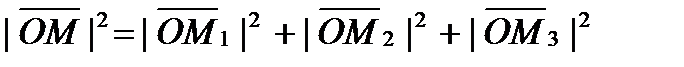 , т.е.
, т.е.
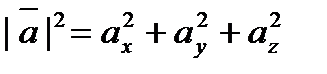 .
.
Отсюда
т.е. модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.
Пусть углы вектора 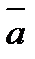 с осями Ox, Oy и Oz соответственно равны α, β, γ. По свойству проекции вектора на ось, имеем
с осями Ox, Oy и Oz соответственно равны α, β, γ. По свойству проекции вектора на ось, имеем
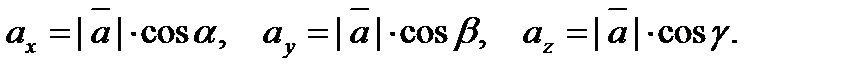 (5.5)
(5.5)
Или, что то же самое,
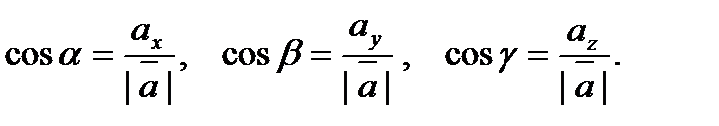
Числа 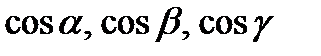 называются направляющими косинусами вектора
называются направляющими косинусами вектора 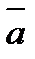 .
.
Подставим выражения (5.5) в равенство (5.4), получаем
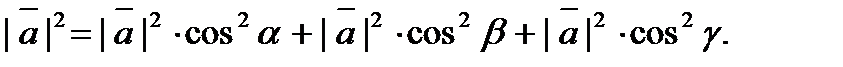
Сократив на 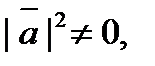 получим соотношение
получим соотношение
т.е. сумма направляющих косинусов ненулевого вектора равна единице.
Легко заметить, что координатами единичного вектора 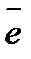 являются числа
являются числа 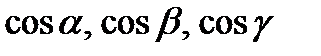 , т.е.
, т.е. 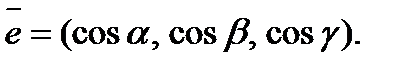
Итак, задав координаты вектора, всегда можно определить его модуль и направление, т.е. сам вектор.
21.Коллинеарные и компланарные вектора. Условия коллинеарности и компланарности.
Векторы 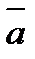 и
и 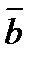 называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают 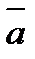 ||
|| 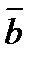 .
.
Коллинеарные векторы могут быть направлены одинаково или противоположно.
Нулевой вектор считается коллинеарным любому вектору.
Два вектора 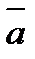 и
и 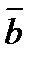 называются равными (
называются равными (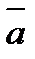 =
= 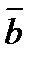 ), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку
О пространства.
На рисунке 1 векторы образуют прямоугольник. Справедливо равенство 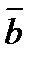 =
= 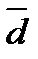 , но
, но 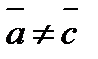 . Векторы
. Векторы 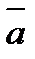 и
и 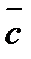 – противоположные,
– противоположные, 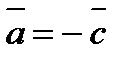 . Равные векторы также называют свободными.
. Равные векторы также называют свободными.
Три вектора в пространстве называются компланарными,
если они лежат в одной плоскости или в параллельных
плоскостях.
Если среди трех векторов хотя бы один нулевой
или два любых коллинеарны, то такие векторы компланарны.



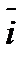 ,
, 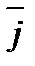 ,
, 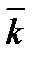 соответственно (см. рис 12).
соответственно (см. рис 12).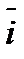
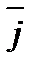
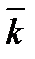
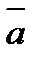 пространства и совместим его начало с началом координат:
пространства и совместим его начало с началом координат: 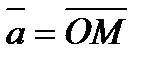 .
.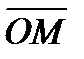 плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с координатными осями обозначим соответственно через M 1, М 2 и М 3. Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор
плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с координатными осями обозначим соответственно через M 1, М 2 и М 3. Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор 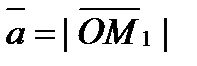 , пр y
, пр y 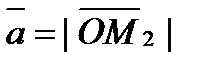 , пр z
, пр z 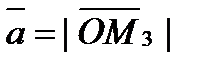 . По определению суммы нескольких векторов находим
. По определению суммы нескольких векторов находим 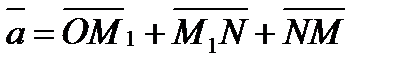
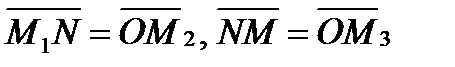 , то
, то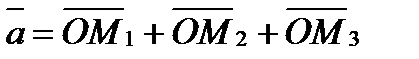 (5.1)
(5.1)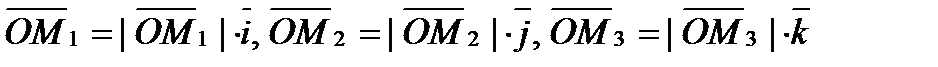 (5.2)
(5.2)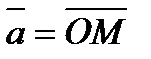 на оси Ox, Oy и Oz соответственно через
на оси Ox, Oy и Oz соответственно через 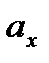 ,
, 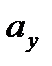 и
и 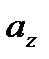 , т.е.
, т.е. 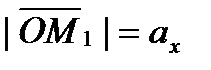 ,
, 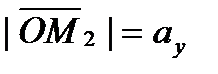 ,
, 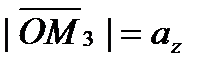 . Тогда из равенств (5.1) и (5.2) получаем
. Тогда из равенств (5.1) и (5.2) получаем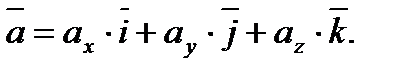
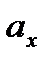 ,
, 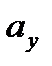 ,
, 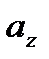 называются координатами вектора
называются координатами вектора 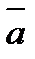 , т.е. координаты вектора есть его проекции на соответствующие координатные оси.
, т.е. координаты вектора есть его проекции на соответствующие координатные оси.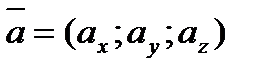 .
.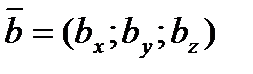 означает, что
означает, что 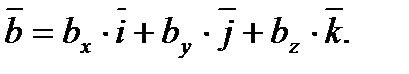
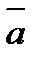 , можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно написать
, можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно написать 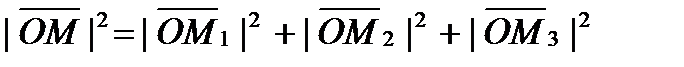 , т.е.
, т.е.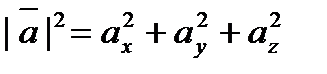 .
.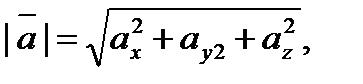
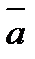 с осями Ox, Oy и Oz соответственно равны α, β, γ. По свойству проекции вектора на ось, имеем
с осями Ox, Oy и Oz соответственно равны α, β, γ. По свойству проекции вектора на ось, имеем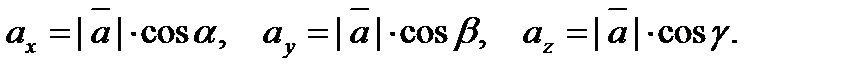 (5.5)
(5.5)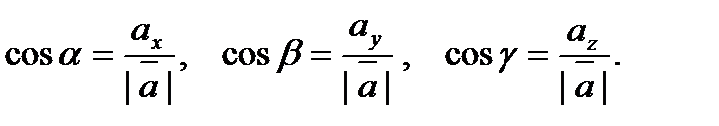
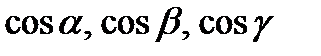 называются направляющими косинусами вектора
называются направляющими косинусами вектора 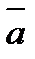 .
.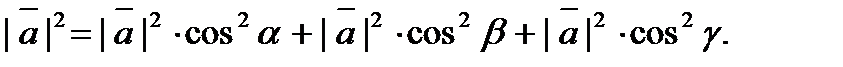
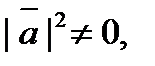 получим соотношение
получим соотношение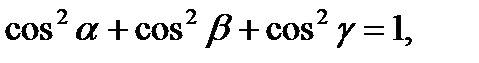
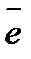 являются числа
являются числа 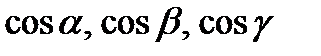 , т.е.
, т.е. 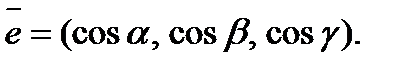
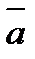 и
и 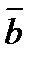 называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают 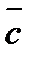
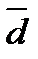
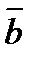
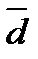 , но
, но 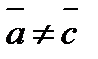 . Векторы
. Векторы 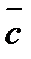 – противоположные,
– противоположные, 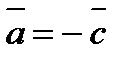 . Равные векторы также называют свободными.
. Равные векторы также называют свободными.


