Как на счёт матриц?:) Знаю, знаю, соскучились. В практических задачах широко распространенная матричная запись квадратичных форм. Объяснения опять начну с формы линейной, например, от трёх переменных: 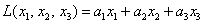 . Её можно записать, как произведение двух матриц:
. Её можно записать, как произведение двух матриц:
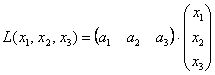
И действительно, выполняя матричное умножение, получаем матрицу «один на один»:  , единственный элемент которой можно эквивалентно записать вне матрицы:
, единственный элемент которой можно эквивалентно записать вне матрицы:  .
.
Легко понять, что линейная форма «эн» переменных записывается в виде:

Квадратичная форма представима в виде произведения уже трёх матриц:
 , где:
, где:
 – столбец переменных;
– столбец переменных;
 – его транспонированная строка;
– его транспонированная строка;
 – матрица квадратичной формы.
– матрица квадратичной формы.
Это так называемая симметрическая матрица, на главной диагонали которой расположены коэффициенты  при квадратах неизвестных, а симметрично относительно неё – «смешанные» коэффициенты, причём, строго на «своих местах» (например,
при квадратах неизвестных, а симметрично относительно неё – «смешанные» коэффициенты, причём, строго на «своих местах» (например,  – в 1-й строке, 3-м столбце и 1-м столбце, 3-й строке).
– в 1-й строке, 3-м столбце и 1-м столбце, 3-й строке).
Определитель  называют дискриминантом квадратичной формы, а ранг матрицы
называют дискриминантом квадратичной формы, а ранг матрицы 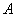 – рангом квадратичной формы.
– рангом квадратичной формы.
Если перемножить три матрицы 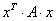 , то получится в точности длинная «простыня» из предыдущего параграфа, но разворачивать её мы, конечно, не будем, а посмотрим, как это происходит в элементарном случае
, то получится в точности длинная «простыня» из предыдущего параграфа, но разворачивать её мы, конечно, не будем, а посмотрим, как это происходит в элементарном случае 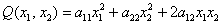 . Согласно общей формуле, матричная запись данной формы имеет следующий вид:
. Согласно общей формуле, матричная запись данной формы имеет следующий вид:

И в самом деле:

далее:

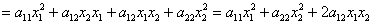 , в чём и требовалось убедиться.
, в чём и требовалось убедиться.
Как вариант, сначала можно было перемножить правые матрицы, и затем первую матрицу умножить на полученный результат.
Вам понравилось так же, как и мне? Ну тогда пример для самостоятельного решения =)
Пример 1
Записать квадратичную форму в матричном виде и выполнить проверку. Определить дискриминант и ранг формы.
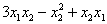
…что-то смущает?;) Краткое решение и ответ в конце урока! Статьи об определителе и ранге матрицы – в помощь.
После чего разберём аналогичную задачу с формой трёх переменных:
Пример 2
Записать матрицу квадратичной формы, найти её ранг и дискриминант

Решение: сбросим тяжёлую ношу лишних формул, и будем ориентироваться на сами члены:
– слагаемое  дважды содержит 1-ю переменную, поэтому
дважды содержит 1-ю переменную, поэтому  ;
;
– из аналогичных соображений определяем  и сразу записываем результаты на главную диагональ симметрической матрицы:
и сразу записываем результаты на главную диагональ симметрической матрицы: 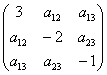 .
.
Так как в слагаемое  входят 1-я и 2-я переменная, то
входят 1-я и 2-я переменная, то  (не забываем поделить на 2) и данный коэффициент занимает свои законные места:
(не забываем поделить на 2) и данный коэффициент занимает свои законные места:  .
.
Поскольку в форме отсутствует член с произведением  (а точнее, присутствует с нулевым множителем:
(а точнее, присутствует с нулевым множителем: 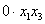 ), то
), то  , и на холст отправляются два нуля:
, и на холст отправляются два нуля:  .
.
И, наконец, из слагаемого  определяем
определяем  , после чего картина завершена:
, после чего картина завершена:
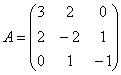 – матрица квадратичной формы. Вот так-то оно бывает – мы не только не испугались «страшных обозначений»
– матрица квадратичной формы. Вот так-то оно бывает – мы не только не испугались «страшных обозначений»  , но и заставили их работать на себя!
, но и заставили их работать на себя!
По условию не требовалось записывать матричное уравнение, однако науки ради:

Желающие могут перемножить три матрицы, в результате чего должна получиться исходная квадратичная форма.
dr
Теперь определим ранг формы. Он равен рангу матрицы 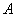 . Так как в матрице есть хотя бы один ненулевой элемент, например,
. Так как в матрице есть хотя бы один ненулевой элемент, например,  , то ранг не меньше единицы. Теперь вычислим минор
, то ранг не меньше единицы. Теперь вычислим минор  , значит, ранг не меньше двух. И осталось проверить минор 3-го порядка, т.е. определитель всей матрицы. Здесь я ко второму столбцу прибавлю третий и раскрою определитель по 3-й строке:
, значит, ранг не меньше двух. И осталось проверить минор 3-го порядка, т.е. определитель всей матрицы. Здесь я ко второму столбцу прибавлю третий и раскрою определитель по 3-й строке:
 , значит,
, значит, 
Если не очень понятно, что к чему, обязательно изучите статью о ранге матрицы – это довольно замысловатая задачка, и перед нами оказался лишь простой случай, когда угловые миноры не равны нулю.
Дискриминант квадратичной формы получен автоматом.
Ответ:  , ранг равен трём, дискриминант
, ранг равен трём, дискриминант 
Следующее задание для самостоятельного решения:
Пример 3
Восстановить квадратичную форму по её матрице

При этом не нужно вспоминать никаких формул! Решение почти устное:
– сначала смотрим на главную диагональ и записываем слагаемые с квадратами переменных;
– затем анализируем симметричные элементы 1-й строки (или 1-го столбца), и записываем все слагаемые, в которые входит 1-я переменная (не забывая удвоить коэффициенты);
– далее смотрим на оставшиеся симметричные элементы 2-й строки (справа от диагонали) либо 2-го столбца (ниже диагонали) и записываем соответствующие парные произведения (с удвоенными коэффициентами!).
– и, наконец, анализируем правую нижнюю пару симметричных чисел.
Подробное решение и ответ в конце урока.



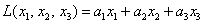 . Её можно записать, как произведение двух матриц:
. Её можно записать, как произведение двух матриц:
 , единственный элемент которой можно эквивалентно записать вне матрицы:
, единственный элемент которой можно эквивалентно записать вне матрицы:  .
.
 , где:
, где: – столбец переменных;
– столбец переменных; – его транспонированная строка;
– его транспонированная строка; – матрица квадратичной формы.
– матрица квадратичной формы. при квадратах неизвестных, а симметрично относительно неё – «смешанные» коэффициенты, причём, строго на «своих местах» (например,
при квадратах неизвестных, а симметрично относительно неё – «смешанные» коэффициенты, причём, строго на «своих местах» (например,  – в 1-й строке, 3-м столбце и 1-м столбце, 3-й строке).
– в 1-й строке, 3-м столбце и 1-м столбце, 3-й строке). называют дискриминантом квадратичной формы, а ранг матрицы
называют дискриминантом квадратичной формы, а ранг матрицы  – рангом квадратичной формы.
– рангом квадратичной формы. , то получится в точности длинная «простыня» из предыдущего параграфа, но разворачивать её мы, конечно, не будем, а посмотрим, как это происходит в элементарном случае
, то получится в точности длинная «простыня» из предыдущего параграфа, но разворачивать её мы, конечно, не будем, а посмотрим, как это происходит в элементарном случае  . Согласно общей формуле, матричная запись данной формы имеет следующий вид:
. Согласно общей формуле, матричная запись данной формы имеет следующий вид:


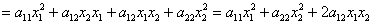 , в чём и требовалось убедиться.
, в чём и требовалось убедиться.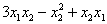

 дважды содержит 1-ю переменную, поэтому
дважды содержит 1-ю переменную, поэтому  ;
; и сразу записываем результаты на главную диагональ симметрической матрицы:
и сразу записываем результаты на главную диагональ симметрической матрицы: 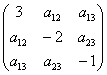 .
. входят 1-я и 2-я переменная, то
входят 1-я и 2-я переменная, то  (не забываем поделить на 2) и данный коэффициент занимает свои законные места:
(не забываем поделить на 2) и данный коэффициент занимает свои законные места:  .
. (а точнее, присутствует с нулевым множителем:
(а точнее, присутствует с нулевым множителем: 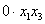 ), то
), то  , и на холст отправляются два нуля:
, и на холст отправляются два нуля:  .
. определяем
определяем  , после чего картина завершена:
, после чего картина завершена: 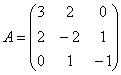 – матрица квадратичной формы. Вот так-то оно бывает – мы не только не испугались «страшных обозначений»
– матрица квадратичной формы. Вот так-то оно бывает – мы не только не испугались «страшных обозначений»  , но и заставили их работать на себя!
, но и заставили их работать на себя!
 , то ранг не меньше единицы. Теперь вычислим минор
, то ранг не меньше единицы. Теперь вычислим минор  , значит, ранг не меньше двух. И осталось проверить минор 3-го порядка, т.е. определитель всей матрицы. Здесь я ко второму столбцу прибавлю третий и раскрою определитель по 3-й строке:
, значит, ранг не меньше двух. И осталось проверить минор 3-го порядка, т.е. определитель всей матрицы. Здесь я ко второму столбцу прибавлю третий и раскрою определитель по 3-й строке: , значит,
, значит, 
 , ранг равен трём, дискриминант
, ранг равен трём, дискриминант 




