Из набора n ценных бумаг можно сформировать бесконечное число портфелей. Необходимо ли инвестору проводить оценку всех этих портфелей? К счастью, ответом на это вопрос является «нет». Инвестор должен рассмотреть только подмножество оптимальных портфелей, каждый из которых обеспечивает максимально ожидаемую доходность для некоторого фиксированного уровня риска или минимальный уровень риска для некоторого значения ожидаемой доходности. Набор таких портфелей называется эффективным множеством.
Графически эффективным множеством будет часть верхней левой границы достижимого множества между точками E и S  . Действительно, зафиксируем уровень математического ожидания портфеля прямой
. Действительно, зафиксируем уровень математического ожидания портфеля прямой  (рис.2.3.1.). Тогда точка этой прямой, которой соответствует наименьшее среднее квадратическое отклонение, будет лежать на левой границе достижимого множества. С другой стороны, можно зафиксировать уровень риска, т.е. среднего квадратического отклонения, прямой
(рис.2.3.1.). Тогда точка этой прямой, которой соответствует наименьшее среднее квадратическое отклонение, будет лежать на левой границе достижимого множества. С другой стороны, можно зафиксировать уровень риска, т.е. среднего квадратического отклонения, прямой 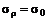 . Тогда оптимальному портфелю с уровнем риска
. Тогда оптимальному портфелю с уровнем риска  будет соответствовать точка этой прямой, лежащая на верхней границе достижимого множества (рис.2.3.1). Эффективное множество является выпуклым вверх.
будет соответствовать точка этой прямой, лежащая на верхней границе достижимого множества (рис.2.3.1). Эффективное множество является выпуклым вверх.

Рис 2.3.1. Определение местоположения эффективного множества
Все остальные портфели достижимого множества будут неэффективными.
Кривая эффективного множества предполагает бесконечное множество точек на ней. Перебрать все точки достижимого множества для определения эффективного невозможно.
Марковиц предложил метод его определения, который построен на ряде предположений, часть из которых относится к условиям принятия инвестиционных решений – к свойствам фондового рынка, другая часть – к поведению инвестора.
Принимая, что величина капитала инвестора равна 1 и распределена между n ценными бумагами портфеля, по известным правилам теории вероятностей можно выразить математическое ожидание доходности  портфеля и его дисперсию
портфеля и его дисперсию 
 , (2.3.1)
, (2.3.1)
 , (2.3.2)
, (2.3.2)
где 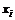 - доля капитала, вложенного в
- доля капитала, вложенного в  -ю ценную бумагу,
-ю ценную бумагу,  - математическое ожидание доходности
- математическое ожидание доходности  -ой ценной бумаги,
-ой ценной бумаги,  - ковариация между доходностями ценных бумаг
- ковариация между доходностями ценных бумаг  и
и  .
.
Инвестор преследует противоречивую цель, стремясь одновременно достичь и наибольшей доходности, и наименьшего риска. Марковиц решал задачу минимизации риска портфеля при обеспечении заданного уровня его доходности. Выпуклость эффективного множества обеспечивает единственность решения оптимизационной задачи.
Найдем вектор распределения капитала по n ценным бумагам  , который минимизирует квадратичную форму (2.3.2) при выполнении ограничений
, который минимизирует квадратичную форму (2.3.2) при выполнении ограничений
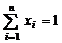 ,
,
 .
.
Эта задача при наличии только ограничений-равенств относится к классу классических задач квадратичной оптимизации. Классический метод неопределенных множителей Лагранжа даст при фиксированном значении математического ожидания доходности лишь одну точку эффективного множества. Но эффективное множество содержит несчетное множество точек.
К тому же этот метод допускает отрицательные значения  , что на практике означает допустимость для всех инвесторов «коротких» продаж ценных бумаг. «Короткая» продажа происходит сначала путём займа ценных бумаг, а затем погашения этого займа такими же ценными бумагами. Такое предположение не всегда допустимо.
, что на практике означает допустимость для всех инвесторов «коротких» продаж ценных бумаг. «Короткая» продажа происходит сначала путём займа ценных бумаг, а затем погашения этого займа такими же ценными бумагами. Такое предположение не всегда допустимо.
Однако наложение дополнительных ограничений-неравенств, например,

существенно усложняет нахождение решения.
Предложенное Марковицем решение основано на введенном им понятии «угловых» портфелей.
Значения параметра 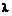 ,
, 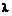
 , где хотя бы одна из функций
, где хотя бы одна из функций  вектора решений
вектора решений  является непрерывной кусочно-линейной, т.е. при изменении
является непрерывной кусочно-линейной, т.е. при изменении 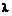 от 0 до
от 0 до  её производные по
её производные по 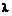 могут терпеть разрыв, называются угловыми, а соответствующие им портфели – «угловыми» портфелями.
могут терпеть разрыв, называются угловыми, а соответствующие им портфели – «угловыми» портфелями.
Марковиц установил замечательное свойство «угловых» портфелей: участок эффективного множества между смежными угловыми портфелями описывается линейной комбинацией этих портфелей. Иначе, если  и
и  - смежные угловые точки, то для любого
- смежные угловые точки, то для любого  ,
, 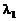 <
<  <
<  , векторы, вычисляемые как
, векторы, вычисляемые как
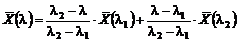 ,
,
определяют участок эффективного множества. При отсутствии ограничений-неравенств функции  - линейные, точка
- линейные, точка 
 является угловой по определению.
является угловой по определению.
Для описания эффективного множества используется вспомогательная прямая, которая является касательной к эффективному множеству. Тогда, изменяя наклон этой касательной от минимального до максимального значения, можно получить описание всего эффективного множества как совокупность точек касания.
Уравнение касательной к некоторой функции 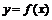 в точке
в точке  имеет вид
имеет вид
 .
.
Запишем его в следующем виде
 .
.
Сделаем замену
 ,
,
 .
.
Таким образом, на плоскости  строим двухпараметрическое семейство прямых, описываемых следующим уравнением при различных а:
строим двухпараметрическое семейство прямых, описываемых следующим уравнением при различных а:
 , (2.3.3)
, (2.3.3)
где  - некоторое число и
- некоторое число и 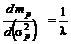 .
.
Таким образом, величина 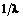 есть тангенс угла наклона семейства прямых к оси
есть тангенс угла наклона семейства прямых к оси  и, следовательно, отражает предпочтение «риск-доходность» инвестора, выбравшего на эффективном фронте точку, касательную с данной прямой, в качестве оптимального портфеля.
и, следовательно, отражает предпочтение «риск-доходность» инвестора, выбравшего на эффективном фронте точку, касательную с данной прямой, в качестве оптимального портфеля.
Запишем уравнение, характеризующее семейство прямых в следующем виде:
 .
.
Не все точки на этих прямых соответствуют каким-либо портфелям, а только те, которые принадлежат допустимому множеству. У касательной прямой такая точка одна. При уменьшении а прямая, принадлежащая параметрическому семейству сдвигается вверх и при минимальном а занимает касательное положение.
Подставив в (2.3.3) вместо 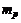 и
и  соответственно (2.3.1) и (2.3.2) получаем
соответственно (2.3.1) и (2.3.2) получаем
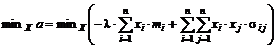 . (2.3.4)
. (2.3.4)
Будем решать задачу квадратичного программирования, используя правило множителей Лагранжа с ограничениями типа равенств и неравенств.

при условиях

или

Запишем функцию Лагранжа в виде
L= 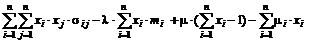 .
.
Ищем решение системы

в виде вектора  , где
, где 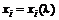 ,
,  ,
,  ,
,  .
.
Проверяем условие неотрицательности всех компонент вектора  , кроме
, кроме  . Т. к.
. Т. к.  , то вся положительная полуось разбивается на конечное число промежутков, в каждом из которых определены
, то вся положительная полуось разбивается на конечное число промежутков, в каждом из которых определены 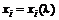 .
.
Таким образом, можно получить вектор решений как функций от 
 . (2.3.5)
. (2.3.5)
При изменении 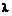 от 0 до
от 0 до  вектора решений опишут все точки касания, т.е. всё эффективное множество.
вектора решений опишут все точки касания, т.е. всё эффективное множество.
Как видно из (2.3.4) точка  определяет эффективный портфель с минимальным риском, а
определяет эффективный портфель с минимальным риском, а  - портфель с максимально возможной доходностью и риском. Определяем угловые значения
- портфель с максимально возможной доходностью и риском. Определяем угловые значения 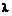 . Подставляя их в (2.3.5), получим «угловые» портфели. Теперь, составляя линейные комбинации «угловых» портфелей, можно построить кривую эффективного множества.
. Подставляя их в (2.3.5), получим «угловые» портфели. Теперь, составляя линейные комбинации «угловых» портфелей, можно построить кривую эффективного множества.
Метод нахождения угловых портфелей, названный Марковицем методом критических линий, с последующим нахождением как оптимального портфеля, так и эффективного множества широко используется и в настоящее время.
Рассмотрим подробнее метод критических линий для случая трёх видов ценных бумаг.
Пример 2.3.1. Первоначальный капитала инвестора распределен между трёмя видами ценных бумаг. Известны математические ожидания доходностей за месяц и ковариационная матрица
М=  ,
, 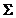 =
=  .
.
Определить эффективное множество, используя метод «угловых» портфелей.
Решение. Пусть 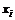 - доля капитала, вложенного в
- доля капитала, вложенного в  -ю ценную бумагу,
-ю ценную бумагу,  . Дисперсия и математическое ожидания доходности портфеля равны
. Дисперсия и математическое ожидания доходности портфеля равны
 ,
, 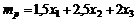 .
.
Решаем задачу

 ,
,

Функция Лагранжа будет иметь вид

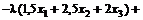

 .
.
Решаем следующую систему уравнений:

Будем рассматривать следующие случаи:
1) 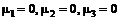 . Тогда система уравнений имеет вид
. Тогда система уравнений имеет вид

Решая систему линейных неоднородных уравнений, получаем вектор решений 
Проверяем условие неотрицательности, учитывая, что 

Решением полученной системы будет  .
.
2)  . Тогда решением системы
. Тогда решением системы

будет
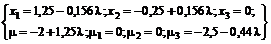
Система, составленная для проверки условия неотрицательности, не имеет решений.
3)  . Тогда решением системы
. Тогда решением системы

будет

Результатом проверки условия неотрицательности  .
.
4) 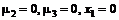 . Тогда решением системы
. Тогда решением системы

будет

Результатом проверки условия неотрицательности будет  .
.
5) 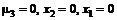 . Тогда решением системы
. Тогда решением системы

будет

Система, составленная для проверки условия неотрицательности, не имеет решений.
6) 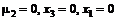 . Тогда решением системы
. Тогда решением системы

будет

Результатом проверки условия неотрицательности будет  .
.
7)  . Тогда решением системы
. Тогда решением системы
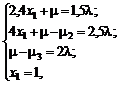
будет

Система, составленная для проверки условия неотрицательности, не имеет решений.
Положительная полуось разбивается на четыре промежутка
 ,
,
в каждом из которых определены 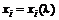 .
.
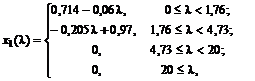


Графики этих функций представлены на рис.2.3.2.

Рис.2.3.2. Нахождение «угловых» портфелей для случая трёх видов ценных бумаг
Таким образом, имеется четыре «угловых» портфеля, которые связаны с ценными бумагами и полностью описывают эффективное множество.
Первый «угловой» портфель – при  - будет описываться следующим вектором весов:
- будет описываться следующим вектором весов:
 .
.
Его ожидаемая доходность и стандартное отклонение соответственно составляют
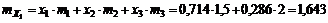 ,
,
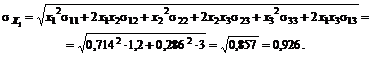
Затем определяем второй «угловой» портфель – при  будет описываться следующим вектором весов:
будет описываться следующим вектором весов:
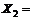
 .
.
Его ожидаемая доходность и стандартное отклонение составляют 1,6955 и 0,951.
Определив второй «угловой» портфель, определяем третий. В данном случае  , и он имеет следующий состав:
, и он имеет следующий состав:

 .
.
Эти веса теперь могут быть использованы для вычисления ожидаемой доходности и стандартного отклонения данного портфеля, которые равны соответственно 2,228 и 1,622.

Рис. 2.3.3. Эффективное множество в случае четырёх «угловых» портфелей
И, наконец, четвёртый «угловой» портфель возникает при  . Его состав следующий:
. Его состав следующий:

 ,
,
и соответственно ожидаемая доходность и стандартное отклонение определяются только бумагами второго вида и равны 2,5 и 2,25.
Составляя всевозможные линейные комбинации каждых двух соседних «угловых» портфелей, получаем эффективное множество (рис. 2.3.3).
Пример2.3.2. В условиях предыдущей задачи найти портфель, для которого ожидаемая доходность равна 2.
Решение. Искомый портфель является линейной комбинацией второго и третьего «угловых» портфелей с ожидаемыми доходностями 1,6955 и 2,228 соответственно. Значит, из уравнения
 ,
,
т.е.
 ,
,
находим  . Таким образом, искомый портфель будет иметь вид
. Таким образом, искомый портфель будет иметь вид

 +0,57
+0,57  =
=  .
.
Получили тот же результат, что и в примере 2.1.2, где эта же задача решалась методом неопределенных множителей Лагранжа.
Упражнения
1. Найти «угловые» портфели и нарисовать схематически эффективное множество, если даны вектор ожидаемых доходностей, и ковариационная матрица
М=  ,
, 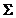 =
=  .
.
2. Решить предыдущую задачу при условиях
М=  ,
, 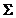 =
=  .
.
3. В условиях первой задачи вычислить ожидаемую доходность и стандартное отклонение «угловых» портфелей.
4. Используя пример 2.3.1 из §2.3, найти портфель, которому соответствует ожидаемая доходность, равная
а) 1,65;
б) 2,4.
Вычислить для него среднеквадратическое отклонение.
5. Построить «угловые» портфели, если известны вектор ожидаемых доходностей и ковариационная матрица
М=  ,
, 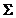 =
= 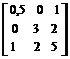 .
.
6. Почему большинство инвесторов предпочитают иметь диверсифицированные портфели, вместо того, чтобы вкладывать все свои средства в один финансовый актив? Для объяснения ответа используйте изображения достижимого и эффективного множеств.



 . Действительно, зафиксируем уровень математического ожидания портфеля прямой
. Действительно, зафиксируем уровень математического ожидания портфеля прямой  (рис.2.3.1.). Тогда точка этой прямой, которой соответствует наименьшее среднее квадратическое отклонение, будет лежать на левой границе достижимого множества. С другой стороны, можно зафиксировать уровень риска, т.е. среднего квадратического отклонения, прямой
(рис.2.3.1.). Тогда точка этой прямой, которой соответствует наименьшее среднее квадратическое отклонение, будет лежать на левой границе достижимого множества. С другой стороны, можно зафиксировать уровень риска, т.е. среднего квадратического отклонения, прямой 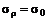 . Тогда оптимальному портфелю с уровнем риска
. Тогда оптимальному портфелю с уровнем риска 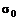 будет соответствовать точка этой прямой, лежащая на верхней границе достижимого множества (рис.2.3.1). Эффективное множество является выпуклым вверх.
будет соответствовать точка этой прямой, лежащая на верхней границе достижимого множества (рис.2.3.1). Эффективное множество является выпуклым вверх.
 портфеля и его дисперсию
портфеля и его дисперсию 
 , (2.3.1)
, (2.3.1) , (2.3.2)
, (2.3.2)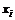 - доля капитала, вложенного в
- доля капитала, вложенного в  -ю ценную бумагу,
-ю ценную бумагу,  - математическое ожидание доходности
- математическое ожидание доходности  - ковариация между доходностями ценных бумаг
- ковариация между доходностями ценных бумаг  .
. , который минимизирует квадратичную форму (2.3.2) при выполнении ограничений
, который минимизирует квадратичную форму (2.3.2) при выполнении ограничений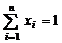 ,
, , что на практике означает допустимость для всех инвесторов «коротких» продаж ценных бумаг. «Короткая» продажа происходит сначала путём займа ценных бумаг, а затем погашения этого займа такими же ценными бумагами. Такое предположение не всегда допустимо.
, что на практике означает допустимость для всех инвесторов «коротких» продаж ценных бумаг. «Короткая» продажа происходит сначала путём займа ценных бумаг, а затем погашения этого займа такими же ценными бумагами. Такое предположение не всегда допустимо.
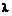 ,
,  , где хотя бы одна из функций
, где хотя бы одна из функций  вектора решений
вектора решений  является непрерывной кусочно-линейной, т.е. при изменении
является непрерывной кусочно-линейной, т.е. при изменении  её производные по
её производные по  и
и  - смежные угловые точки, то для любого
- смежные угловые точки, то для любого  ,
, 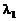 <
< 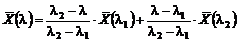 ,
,
 является угловой по определению.
является угловой по определению.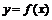 в точке
в точке  имеет вид
имеет вид .
. .
. ,
, .
. строим двухпараметрическое семейство прямых, описываемых следующим уравнением при различных а:
строим двухпараметрическое семейство прямых, описываемых следующим уравнением при различных а: , (2.3.3)
, (2.3.3) - некоторое число и
- некоторое число и 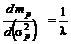 .
.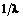 есть тангенс угла наклона семейства прямых к оси
есть тангенс угла наклона семейства прямых к оси  и, следовательно, отражает предпочтение «риск-доходность» инвестора, выбравшего на эффективном фронте точку, касательную с данной прямой, в качестве оптимального портфеля.
и, следовательно, отражает предпочтение «риск-доходность» инвестора, выбравшего на эффективном фронте точку, касательную с данной прямой, в качестве оптимального портфеля. .
.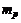 и
и 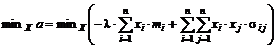 . (2.3.4)
. (2.3.4)


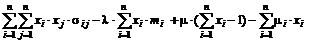 .
.
 , где
, где 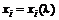 ,
,  ,
,  ,
,  .
. . Т. к.
. Т. к.  , то вся положительная полуось разбивается на конечное число промежутков, в каждом из которых определены
, то вся положительная полуось разбивается на конечное число промежутков, в каждом из которых определены 
 вектора решений опишут все точки касания, т.е. всё эффективное множество.
вектора решений опишут все точки касания, т.е. всё эффективное множество. определяет эффективный портфель с минимальным риском, а
определяет эффективный портфель с минимальным риском, а  - портфель с максимально возможной доходностью и риском. Определяем угловые значения
- портфель с максимально возможной доходностью и риском. Определяем угловые значения  ,
, 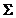 =
=  .
. . Дисперсия и математическое ожидания доходности портфеля равны
. Дисперсия и математическое ожидания доходности портфеля равны ,
, 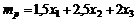 .
.
 ,
,

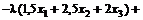

 .
.
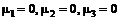 . Тогда система уравнений имеет вид
. Тогда система уравнений имеет вид


 .
. . Тогда решением системы
. Тогда решением системы
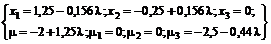
 . Тогда решением системы
. Тогда решением системы

 .
.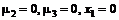 . Тогда решением системы
. Тогда решением системы

 .
.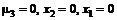 . Тогда решением системы
. Тогда решением системы

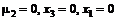 . Тогда решением системы
. Тогда решением системы

 .
. . Тогда решением системы
. Тогда решением системы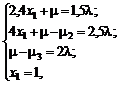

 ,
,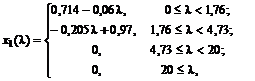



 .
.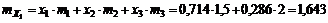 ,
,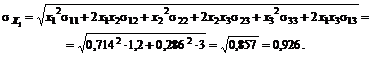
 будет описываться следующим вектором весов:
будет описываться следующим вектором весов: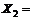
 .
. , и он имеет следующий состав:
, и он имеет следующий состав:
 .
.
 . Его состав следующий:
. Его состав следующий:
 ,
, ,
, ,
, . Таким образом, искомый портфель будет иметь вид
. Таким образом, искомый портфель будет иметь вид
 =
=  .
. ,
,  .
. ,
,  .
. ,
, 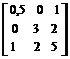 .
.


