Рассмотрим произвольную бесконечно длинную направляющую систему, ориентированную вдоль оси Z. Будем полагать, что направляющая система не вносит потерь и однородна, т.е.:
– форма конечного сечения не зависит от координаты Z;
– параметры среды, в которой распространяется ЭМП, и граничные
условия, которым удовлетворят поле, не зависят от координаты Z.
При отсутствии сторонних источников  должны удовлетворять однородным уравнениям Гельмгольца:
должны удовлетворять однородным уравнениям Гельмгольца:

Зависимость  и
и  от координаты Z описывается множителем
от координаты Z описывается множителем  ,
,
В однородные уравнения Гельмгольца при  и
и  получим:
получим:
 (16)
(16)
Обозначение
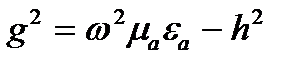 (17)
(17)
где g - волновое число.
Уравнения (16) эквивалентно трем скалярным уравнениям для продольной и двух поперечных составляющих. Поперечные составляющие можно выразить через продольные с помощью соотношений, вытекающих из дифференциальных уравнений Максвелла.
Преобразуем однородные уравнения Максвелла:
 (18)
(18)

Решая систему (18) относительно  получаем:
получаем:


 (19)
(19)
Аналогично, из (19) 
 (20)
(20)
Система уравнений (19)-(20 ) связывает поперечные и продольные составляющие поля в декартовой системе координат. Для выражения этой связи в произвольной системе координат перейдем к векторной форме уравнений.Введем вектор  . Подставляя в это выражение вместо
. Подставляя в это выражение вместо  и
и  их значения из (19) - (20), получим:
их значения из (19) - (20), получим:

 .
.
Введя обозначение 
и учитывая, что 
получим  (21 )
(21 )
Аналогично, получается равенство
Таким образом, для нахождения структуры полного поля необходимо решить с учетом граничных условий два дифференциальных уравнения:
 (22)
(22)
и воспользоваться равенствами (21) для определения поперечных составляющих.
Критическая частота. Критическая длина волны

h, является вещественной величиной, если
 (23)
(23)
и мнимой величиной, если
 (24)
(24)
В первом случае фаза изменяется вдоль оси Z по линейному закону, что является признаком распространения волны с постоянной фазовой скоростью вдоль этой оси. Во втором случае вдоль оси Z фаза остается постоянной, а амплитуда убывает по экспоненте, что является признаком отсутствия переноса энергии вдоль направляющей системы.
Частота определяется из условия
 (25)
(25)
называется критической.
 (26)
(26)
Соответствующая этой частоте критическая длина волны равна:
 (27)
(27)
Тогда  (28)
(28)
где 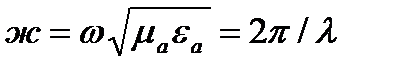 - волновое число, а
- волновое число, а  - длина волны в среде с параметрами
- длина волны в среде с параметрами 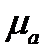 и
и  .
.
Согласно (24) свободное распространение волны по направляющей системе имеет место лишь на частотах, превышающих критическую  .
.
Назовем длиной волны  в направляющей системе минимальное расстояние между поперечными сечениями, соответствующими различным значениям координаты Z, в которых колебания сдвинуты по фазе на 2p. Так как зависимость составляющих поля от координаты Z описывается выражением:
в направляющей системе минимальное расстояние между поперечными сечениями, соответствующими различным значениям координаты Z, в которых колебания сдвинуты по фазе на 2p. Так как зависимость составляющих поля от координаты Z описывается выражением:  , то
, то
 (29)
(29)



 должны удовлетворять однородным уравнениям Гельмгольца:
должны удовлетворять однородным уравнениям Гельмгольца:
 от координаты Z описывается множителем
от координаты Z описывается множителем  ,
, и
и  получим:
получим: (16)
(16)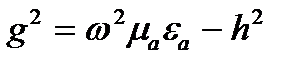 (17)
(17) (18)
(18)
 получаем:
получаем:

 (19)
(19)
 (20)
(20) . Подставляя в это выражение вместо
. Подставляя в это выражение вместо 
 .
.

 (21 )
(21 ) (22)
(22)
 (23)
(23) (24)
(24) (25)
(25) (26)
(26) (27)
(27) (28)
(28)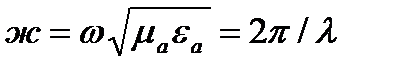 - волновое число, а
- волновое число, а  - длина волны в среде с параметрами
- длина волны в среде с параметрами 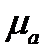 и
и  .
. .
. в направляющей системе минимальное расстояние между поперечными сечениями, соответствующими различным значениям координаты Z, в которых колебания сдвинуты по фазе на 2p. Так как зависимость составляющих поля от координаты Z описывается выражением:
в направляющей системе минимальное расстояние между поперечными сечениями, соответствующими различным значениям координаты Z, в которых колебания сдвинуты по фазе на 2p. Так как зависимость составляющих поля от координаты Z описывается выражением:  , то
, то (29)
(29)

