

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...
Топ:
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Интересное:
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
ЧАСТЬ 1.
МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
МАССОВОГО ОБСЛУЖИВАНИЯ
Уравнения Колмогорова непрерывной
Марковской цепи
Диаграммой переходов состояний марковской цепи в целом (как непрерывной, так и дискретной) является направленный (ориентированный) граф состояний, вершины которого соответствуют состояни-
ям, а ребра – переходам между этими состояниями. Каждое ребро должно быть помечено интенсивностью 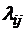 (для непрерывной марковской цепи) или вероятностью
(для непрерывной марковской цепи) или вероятностью 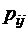 (для дискретной марковской цепи) соответствующего перехода в потоке событий. Цепь Маркова полностью определяется ее диаграммой переходов между состояниями, то есть ее графом состояний.
(для дискретной марковской цепи) соответствующего перехода в потоке событий. Цепь Маркова полностью определяется ее диаграммой переходов между состояниями, то есть ее графом состояний.
Понятие интенсивности  марковского случайного процесса вводится следующим образом. Пусть вероятность перехода из состояния i в состояние j за время от t до
марковского случайного процесса вводится следующим образом. Пусть вероятность перехода из состояния i в состояние j за время от t до 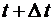 есть
есть
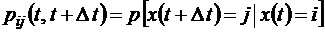 ,
,
согласно формуле (1.1.1). Тогда по определению
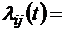 lim
lim 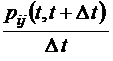
при 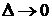 . Для так называемых однородных марковских процессов вероятности переходов не зависят от времени, так что
. Для так называемых однородных марковских процессов вероятности переходов не зависят от времени, так что 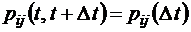 , и тогда
, и тогда 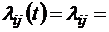 const. Для систем массового обслуживания понятие состояния определяется, как правило, общим числом заявок или требований, находящихся в системе (как в очередях, так и на обслуживании).
const. Для систем массового обслуживания понятие состояния определяется, как правило, общим числом заявок или требований, находящихся в системе (как в очередях, так и на обслуживании).
Исчерпывающей количественной характеристикой марковского процесса является совокупность вероятностей состояний системы, то есть вероятностей 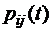 того, что в момент времени t процесс будет находиться в состоянии j (j = 0, 1, 2, …). Таким образом, наша задача заключается в том, чтобы научиться рассчитывать
того, что в момент времени t процесс будет находиться в состоянии j (j = 0, 1, 2, …). Таким образом, наша задача заключается в том, чтобы научиться рассчитывать 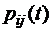 по заданным интенсивностям переходов
по заданным интенсивностям переходов 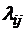 .
.
Рассмотрим, как определяются вероятности состояний по графу состояний [12], приведенному на рис. 2, считая данный случайный процесс марковским. В случайный момент времени t система может находиться в одном из пяти состояний j с вероятностями  (j = 0,
(j = 0,
|
|
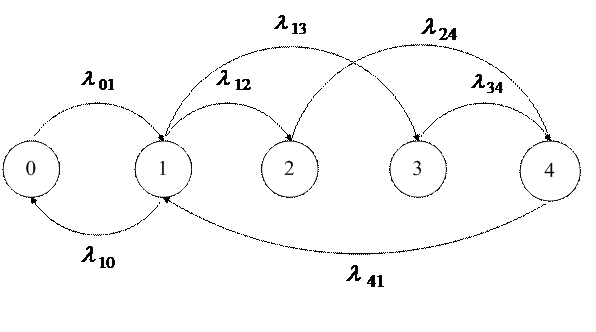
Рис. 2
1, 2, 3, 4). Придадим времени t малое приращение 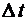 и найдем, например,
и найдем, например, 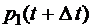 – вероятность того, что в момент времени
– вероятность того, что в момент времени 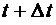 система будет находиться в состоянии 1. А это может произойти в одном из трех взаимоисключающих друг друга случаях: во-первых, если система в момент времени t была в состоянии 1 и за время
система будет находиться в состоянии 1. А это может произойти в одном из трех взаимоисключающих друг друга случаях: во-первых, если система в момент времени t была в состоянии 1 и за время 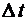 не вышла из него, а также, если в момент t система была в состояниях 0 или 4и за время
не вышла из него, а также, если в момент t система была в состояниях 0 или 4и за время 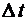 перешла в состояние 1.
перешла в состояние 1.
В этой связи напомним известный результат из курса теории вероятностей: для того чтобы найти полную вероятность какого-либо состояния j, нужно сложить вероятности всех тех событий, которые приводят к этому состоянию, точнее говоря, заканчиваются его исходом, так что
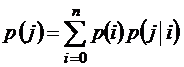
(формула полной вероятности [3; 6]). В нашем случае применение этой формулы, очевидно, будет следующим:
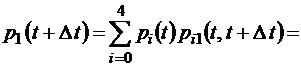 (1.2.1)
(1.2.1)
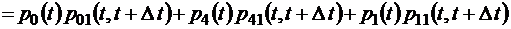 .
.
Здесь первое слагаемое означает вероятность перехода за время 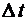 в состояние 1 из состояния 0, если в момент t система находилась в состоянии 0 с вероятностью p 0(t). Второе слагаемое означает аналогичную вероятность, но уже не для состояния 0, а для состояния 4. Последнее же третье слагаемое есть, очевидно, вероятность того, что за время
в состояние 1 из состояния 0, если в момент t система находилась в состоянии 0 с вероятностью p 0(t). Второе слагаемое означает аналогичную вероятность, но уже не для состояния 0, а для состояния 4. Последнее же третье слагаемое есть, очевидно, вероятность того, что за время 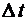 система не выйдет из состояния 1, то есть не перейдет за это время в состояния 0, 2 или 3. Вследствие этого, для того чтобы найти вероятность
система не выйдет из состояния 1, то есть не перейдет за это время в состояния 0, 2 или 3. Вследствие этого, для того чтобы найти вероятность 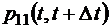 , нужно просто вычесть из единицы вероятности всех тех событий, которые выводят систему из состояния 1*. Вероятность же того, что за время
, нужно просто вычесть из единицы вероятности всех тех событий, которые выводят систему из состояния 1*. Вероятность же того, что за время 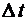 система выйдет из состояния 1, в данном случае есть, очевидно, p 10 + p 12 + p 13, то есть
система выйдет из состояния 1, в данном случае есть, очевидно, p 10 + p 12 + p 13, то есть
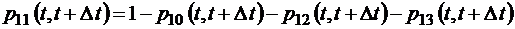 ,
,
и тогда
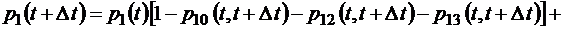
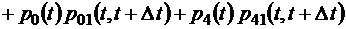 .
.
Раскроем теперь квадратные скобки в правой части этого соотношения, перенесем p1(t) в левую часть и разделим обе части на время 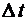 . Получим
. Получим
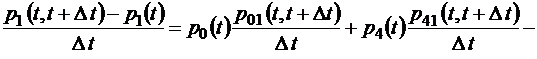
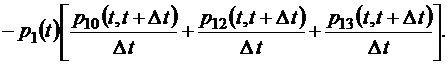
Если теперь устремить время 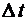 к нулю, то слева получим производную функции p 1(t), а справа – интенсивности марковского процесса λij (t):
к нулю, то слева получим производную функции p 1(t), а справа – интенсивности марковского процесса λij (t):
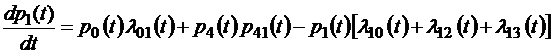 .
.
Аналогичные уравнения можно вывести и для всех остальных состояний системы, так что в итоге мы получим следующую систему квазилинейных дифференциальных уравнений для безусловных вероятностей pi (t):
|
|
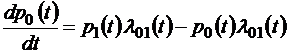 ;
;
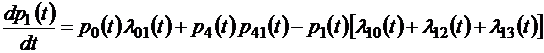 ;
;
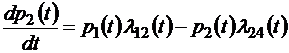 ;
;
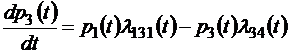 ;
;
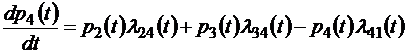 .
.
Эта система уравнений дает возможность найти вероятности pj (t) состояний системы, если заданы их начальные условия pj (0).
В левой части каждого из этих уравнений стоит производная вероятности j -го состояния системы, в правой части – сумма произведений вероятностей тех состояний, из которых ведут стрелки в j -е состояние, на интенсивности соответствующих переходов (соответствующих случайных процессов) минус суммарная интенсивность всех процессов, выводящих систему из j -го состояния, умноженная на вероятность этого состояния. В общем виде такую систему уравнений можно записать как систему с переменными коэффициентами
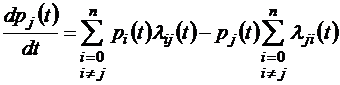 , j = 0, 1, 2, … n (1.2.2)
, j = 0, 1, 2, … n (1.2.2)
или для однородных марковских процессов как
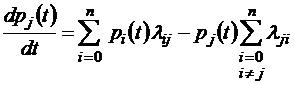 , j = 0, 1, 2, … n, (1.2.3)
, j = 0, 1, 2, … n, (1.2.3)
и в этом случае система (1.2.2) становится системой линейных дифференциальных уравнений (1.2.3).
Заметим, что в этих записях учтено то очевидное обстоятельство, что для состояний системы, не связанных непосредственными переходами друг с другом, можно считать λji = λij = 0.
Уравнения (1.2.2), (1.2.3) носят название уравнений Колмогорова и являются управляющими уравнениями для непрерывного случайного марковского процесса (непрерывной марковской цепи).
Системы дифференциальных уравнений (1.2.2), (1.2.3) решают при начальных условиях, задающих вероятности состояний системы в начальный момент времени при t = 0: p 0(0), p 1(0), … pn (0), причем для любого момента времени t должно быть выполнено условие нормировки
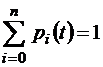 ,
, 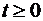 .
.
Это условие можно использовать вместо одного (и при этом любого) из дифференциальных уравнений систем (1.2.2) и (1.2.3).
При составлении уравнений Колмогорова по графу состояний системы удобно ввести понятие потока вероятности. А именно будем называть потоком вероятности, переводящим систему из состояния i в состояние j, произведение вероятности pi (t) состояния, из которого исходит стрелка на графе, на интенсивность λij (t) марковского процесса, переводящего систему по этой стрелке. Уравнения Колмогорова в этом случае составляются по следующему мнемоническому правилу. Производная вероятности любого из состояний системы равна сумме всех потоков вероятности, переводящих систему в это состояние, за вычетом суммы всех потоков вероятности, выводящих систему из этого состояния.
|
|
В пределе при 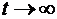 в системе, описываемой линейными дифференциальными уравнениями (1.2.3), в некоторых случаях может установиться режим, в ходе которого система случайным образом меняет свои состояния (или, как говорят, бесконечно блуждает по всем своим состояниям), но их вероятностные характеристики уже не зависят от времени. Говоря другими словами, в этом случае существуют так называемые предельные (или финальные) вероятности стационарных состояний системы pj , и при этом
в системе, описываемой линейными дифференциальными уравнениями (1.2.3), в некоторых случаях может установиться режим, в ходе которого система случайным образом меняет свои состояния (или, как говорят, бесконечно блуждает по всем своим состояниям), но их вероятностные характеристики уже не зависят от времени. Говоря другими словами, в этом случае существуют так называемые предельные (или финальные) вероятности стационарных состояний системы pj , и при этом
lim 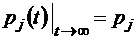 , j = 0, 1, 2, … n.
, j = 0, 1, 2, … n.
Заметим, что предельную вероятность состояния j в этом случае можно трактовать и как среднее относительное время пребывания системы в этом состоянии.
Для вычисления предельных вероятностей нужно, очевидно, все левые части в уравнениях Колмогорова (1.2.3) положить равными нулю и решить полученную систему линейных, но уже алгебраических, а не дифференциальных уравнений
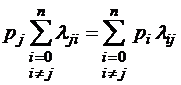 , j = 0, 1, 2, … n (1.2.4)
, j = 0, 1, 2, … n (1.2.4)
(уравнения равновесия соответствующего марковского процесса). При этом стационарный режим существует тогда и только тогда, когда данная система уравнений имеет хотя бы одно ненулевое и вместе с тем не обращающееся в бесконечность решение  , j = 0, 1, 2, … n. Легко видеть, что система (1.2.4) представляет собой систему линейных однородных, то есть не имеющих свободного члена, алгебраических уравнений для вероятностей стационарных состояний p 0, p 1, … pn. Но, как известно из линейной алгебры, такая система уравнений имеет бесчисленное множество решений и позволяет определить неизвестные величины pj только с точностью до некоторого произвольного множителя. В рассматриваемом случае решение, оче-
, j = 0, 1, 2, … n. Легко видеть, что система (1.2.4) представляет собой систему линейных однородных, то есть не имеющих свободного члена, алгебраических уравнений для вероятностей стационарных состояний p 0, p 1, … pn. Но, как известно из линейной алгебры, такая система уравнений имеет бесчисленное множество решений и позволяет определить неизвестные величины pj только с точностью до некоторого произвольного множителя. В рассматриваемом случае решение, оче-
видно, становится единственным, если добавить к системе (1.2.4) условие нормировки
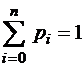 ,
,
взамен которого можно из системы (1.2.4) устранить любое другое, поскольку одно из уравнений этой системы зависит от остальных.
В курсах линейной алгебры доказывается, что такая система имеет одно единственное решение, то есть однозначно определяет вероятности p 0, p 1, …, дающие в сумме единицу. Заметим, что с точки зрения математики вышеописанные действия эквивалентны следующей, подчас более простой, процедуре. А именно, если существует хотя бы одно такое решение 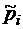 системы уравнений (1.2.4), для которого выполнено неравенство
системы уравнений (1.2.4), для которого выполнено неравенство
|
|
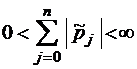 ,
,
то стационарное распределение вероятностей определяется однозначно по формуле
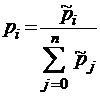 , i = 0, 1, 2, … n.
, i = 0, 1, 2, … n.
Марковской цепи
Иногда, особенно в зарубежной литературе, уравнения Колмогорова непрерывной марковской цепи принято записывать несколько другим способом.
Вернемся еще раз к формуле (1.2.1). Имеем



 ,
,
и тогда

 .
.
Если теперь при Δ t →0 объявить предел отношения  интенсивностью перехода i → i, то получим систему уравнений
интенсивностью перехода i → i, то получим систему уравнений

или для однородной цепи Маркова –
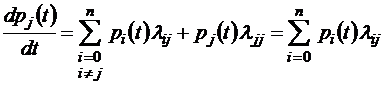 .
.
В матричном виде это будет  , где
, где

– матрица интенсивностей переходов между состояниями,  – вектор вероятностей состояний системы. В стационарном случае, очевидно, должно быть
– вектор вероятностей состояний системы. В стационарном случае, очевидно, должно быть
 или
или 
и так далее. При таком определении λij интенсивности переходов будут удовлетворять условию
 (i =0, 1,2, … n),
(i =0, 1,2, … n),
то есть в этом случае значения λjj (t) нужно искать по формуле

в согласии с системой уравнений Колмогорова (1.2.2).
Простейший поток событий
Потоком событий называется последовательность однородных событий, появляющихся одно за другим в случайные моменты времени. При этом среднее число событий, приходящееся на единицу времени, называется интенсивностью  этого потока событий.
этого потока событий.
С точки зрения математики поток событий может быть описан как случайный процесс X (t), принимающий только целочисленные неубывающие значения 0, 1, 2, … Применительно к системам массового обслуживания процесс X (t) есть просто число заявок или требований, поступивших в СМО за промежуток времени от 0до t.
Введем понятие простейшего потока событий. Простейшим называется поток событий, для которого выполняются следующие три условия, которые мы сформулируем здесь в соответствии с принятой в теории массового обслуживания инженерной терминологией.
Отсутствие последствия (lack of memory). Отсутствие последствия в потоке означает, что для любого момента времени t будущие моменты наступления событий не зависят от того, в какие моменты наступали аналогичные события в прошлом, то есть будущее зависит от прошлого только через настоящее (на языке математики – обычное марковское свойство).
Ординарность. Поток событий называется ординарным, если в каждый момент времени может произойти только одно событие (может появиться только одна заявка). Говоря другими словами, события в таком потоке появляются поодиночке, а не группами.
Стационарность. На языке теории массового обслуживания поток событий называется стационарным, если его вероятностные характеристики, то есть интенсивность и закон распределения промежутков времени между событиями, не меняются со временем. В противном случае поток является нестационарным. На языке теории цепей Маркова это свойство, в соответствии со сказанным выше, означает просто однородность соответствующего марковского процесса по времени.
|
|
Говоря другими словами, простейший поток событий представляет собой однородную цепь Маркова с непрерывным временем, обладающую дополнительно еще и свойством ординарности. Граф такой марковской цепи изображен на рис. 3. На этом рисунке λ – это некоторая пока еще не определенная интенсивность соответствующего марковского процесса. Найдем закон распределения вероятностей событий в этом потоке.
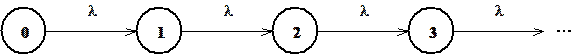
Рис. 3
Очевидно, что для графа состояний, изображенного на этом рисунке (точнее говоря, для случайного марковского процесса, соответствующего этому графу состояний), уравнения Колмогорова (1.2.2) примут следующий вид:
 , k = 1, 2, …
, k = 1, 2, …  . (1.4.1)
. (1.4.1)
Здесь pk (λ) – вероятность того, что за время от 0 до t в систему поступит ровно k заявок (или, что то же самое, произойдет ровно k событий).
Начальные условия к этим уравнениям:
 ;
;  , k =1, 2, …, (1.4.2)
, k =1, 2, …, (1.4.2)
то есть  или
или 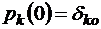 , где
, где  – символ Кронекера:
– символ Кронекера:
 =
= 
Условия (1.4.2), очевидно, означают, что на начальный момент времени заявки в системе отсутствуют.
Для решения системы уравнений (1.4.1) произведем замену, введя новую функцию Uk (t) по правилу 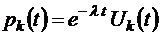 . Тогда уравнения (1.4.1) примут вид
. Тогда уравнения (1.4.1) примут вид
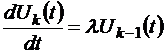 , k = 1, 2, …
, k = 1, 2, …  . (1.4.3)
. (1.4.3)
Начальные условия к этим уравнениям, очевидно, задаются равенствами
 ;
;  , k = 1, 2, …
, k = 1, 2, …
Теперь из системы (1.4.3) имеем
 ;
;  ;
;
 ;
; 
и так далее. В итоге для всех k =1, 2, … получим формулу
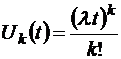 ,
,
так что
 . (1.4.4)
. (1.4.4)
Это и есть знаменитое распределение Пуассона, или, точнее говоря, стационарное распределение Пуассона, поскольку в общем случае для этого распределения 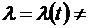 const. Итак, простейший поток событий описывается вероятностным распределением Пуассона, вследствие чего его часто так и называют – поток Пуассона.
const. Итак, простейший поток событий описывается вероятностным распределением Пуассона, вследствие чего его часто так и называют – поток Пуассона.
Заметим, что если в начальный момент времени в системе имеются i > 0 требований, а под pk (t) по-прежнему понимается вероятность того, что за время от 0 до t поступит ровно k заявок, то, как можно показать, в этом случае решение уравнений (1.4.1) даст нам распределение
 , k = i +1, i +2, …
, k = i +1, i +2, …
которое также является одной из разновидностей классического распределения Пуассона.
Далее обозначим через k (t) общее число заявок (требований), поступивших в систему в промежутке времени от 0до t. В этом случае


Таким образом, мы получили, что среднее число требований (заявок), поступивших в систему за промежуток времени от 0 до t, есть просто  . Отсюда в свою очередь следует, что интенсивность λ марковского процесса, описываемого соответствующим графом состояний, определяется формулой
. Отсюда в свою очередь следует, что интенсивность λ марковского процесса, описываемого соответствующим графом состояний, определяется формулой  .
.
Как видим, для простейшего потока событий, рассматриваемого как марковский случайный процесс, физическая интенсивность поступившего в систему потока требований (среднее число этих требований в единицу времени) совпадет с интенсивностью марковского процесса, соответствующего этому потоку заявок. Дисперсия же числа событий (в данном случае – числа заявок, поступивших в систему за интервал времени от 0 до t), очевидно,

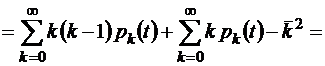

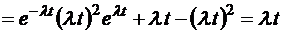 .
.
Таким образом, среднее значение и дисперсия общего числа заявок в простейшем потоке событий одинаковы и равны  . Отсюда следует, что коэффициент вариации
. Отсюда следует, что коэффициент вариации 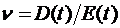 , равный отношению дисперсии к математическому ожиданию и характеризующий степень нерегулярности потока заявок, в данном случае равен единице. Заметим, что для регулярного или детерминированного потока, то есть потока, в котором промежутки времени между двумя последовательными заявками являются постоянными величинами, коэффициент вариации v равен нулю, для большинства же других законов распределения 0 < v < 1.
, равный отношению дисперсии к математическому ожиданию и характеризующий степень нерегулярности потока заявок, в данном случае равен единице. Заметим, что для регулярного или детерминированного потока, то есть потока, в котором промежутки времени между двумя последовательными заявками являются постоянными величинами, коэффициент вариации v равен нулю, для большинства же других законов распределения 0 < v < 1.
Вернемся еще раз к потоку Пуассона и зададимся целью определить закон распределения вероятностей для интервалов, которые разделяют два последовательных события в этом потоке.
Рассмотрим случайную переменную  , представляющую собой промежуток времени между двумя последовательными требованиями, поступающими в систему массового обслуживания. По определению искомая функция распределения
, представляющую собой промежуток времени между двумя последовательными требованиями, поступающими в систему массового обслуживания. По определению искомая функция распределения

– это вероятность того, что интервал времени между двумя последовательными событиями не превзойдет t или, говоря другими словами, F (t) – вероятность того, что хотя бы одно событие произойдет в некотором интервале времени от 0 до t, если оно произошло в начальный момент времени при t = 0.
Применим эту формулу к потоку Пуассона. Ясно, что в этом случае
 ,
,
где  – вероятность того, что промежуток времени между двумя последовательными событиями в потоке, напротив, превзойдет t, то есть вероятность того, что на интервале длины t (от 0 до t) не произошло ни одного события. В силу же формулы (1.4.4) вероятность отсутствия событий за время t есть просто
– вероятность того, что промежуток времени между двумя последовательными событиями в потоке, напротив, превзойдет t, то есть вероятность того, что на интервале длины t (от 0 до t) не произошло ни одного события. В силу же формулы (1.4.4) вероятность отсутствия событий за время t есть просто  и, значит,
и, значит,
 , (1.4.5)
, (1.4.5)
а соответствующая плотность вероятности
 (1.4.6)
(1.4.6)
(напомним в этой связи, что по определению
 ).
).
Это распределение (1.4.6) хорошо известно в теории вероятностей и носит название показательного (или экспоненциального) распределения случайной величины. Следовательно, если моменты наступления требований в систему распределены по закону Пуассона, то промежутки времени между этими моментами имеют экспоненциальный закон распределения.
Покажем, что верно и обратное утверждение, то есть из формулы (1.4.6) можно в свою очередь вывести обратным ходом и закон распределения (1.4.4). В самом деле, очевидно, что
 .
.
Далее, пусть p 1(t) – вероятность того, что за время t в систему придет только одна заявка или, что то же самое, в системе произойдет только одно случайное событие. Пусть это событие произошло в некоторый момент времени τ < t. Это, в свою очередь, означает, что за время t–τ, оставшееся до конца рассматриваемого интервала, в системе не произойдет ни одного случайного события. Вероятность этого для каждого отдельного момента времени (в интервале от τ до t) есть, очевидно,  .
.
В этом случае средняя вероятность отсутствия случайных событий за время от τ до t для всех τ ( ) согласно определению средней величины есть просто
) согласно определению средней величины есть просто
 .
.
Точно так же очевидно, что
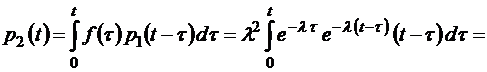

и так далее. В результате мы снова получим распределение чисел появления случайных событий в простейшем потоке (1.4.4).
Как видим, распределение Пуассона и показательное распределение взаимно однозначно связаны между собой или, говоря другими словами, равносильными являются утверждения о том, что процесс является пуассоновским по распределению числа событий и что распределение длительности интервалов этого процесса показательное.
Так, например, если время обслуживания какой-либо системы массового обслуживания имеет экспоненциальное распределение, то число обслуженных за время t заявок также подчиняется закону Пуассона со своей средней интенсивностью обслуживания μ:
 ,
,
то есть можно говорить о том, что навстречу потоку поступающих в систему заявок движется встречный поток обслуживаемых заявок, выводящий заявки из данной системы.
Определим теперь на основе показательного распределения (1.4.6) математическое ожидание (среднее значение) и дисперсию интервала времени между двумя последовательными событиями в простейшем потоке. По определению
 .
.
Проинтегрировав это выражение по частям, получим
 .
.
Дисперсия показательно распределенной величины

 .
.
Интересно выяснить, какая доля промежутков времени между двумя последовательными требованиями в такого рода потоке имеет длину, меньшую, чем ее математическое ожидание, то есть меньшую, чем  . Это, очевидно, будет
. Это, очевидно, будет

 .
.
Доля промежутков времени, которые, наоборот, длиннее, чем  , в этом случае есть
, в этом случае есть  , и тогда их отношение
, и тогда их отношение  – довольно значительная величина.
– довольно значительная величина.
Для полноты картины, а также для проверки и подтверждения истинности полученных результатов необходимо еще продемонстрировать марковское свойство (на языке теории массового обслуживания – свойство отсутствия последствия) полученного нами распределения интервалов между событиями в простейшем потоке (1.4.5). Проще всего это сделать следующим образом. Найдем еще раз F (t) – функцию распределения интервалов времени между событиями в потоке (1.4.4). Для этого повторим вывод формулы для F (t), но уже не для рассмотренного выше отрезка между начальным моментом времени t = 0 и некоторым t, а рассматривая произвольный, в том числе и достаточно удаленный от начальной точки, отрезок времени от t 0 до
t 0 + t, где t 0 – любое фиксированное число. В данном случае событие (приход заявки в систему) происходит внутри отрезка времени от t 0 до t 0 + t (то есть за время, меньшее, чем t 0 + t), но лишь при условии, что это случится не раньше момента времени t 0 (все события, которые имели место до этого времени, нас не интересуют). Очевидно, что тогда функция распределения F (t) будет описываться условной вероятностью
 .
.
Отсюда по формуле для условной вероятности имеем


– уже известный нам закон распределения (1.4.5). Или, говоря другими словами, будущее показательно распределенной случайной величины (после момента времени t 0) не зависит от прошлой истории этой величины (до момента времени t 0), и это распределение остается неизменным во времени. Подчеркнем при этом, что показательное распределение является единственным непрерывным распределением, обладающим этим свойством. В случае же дискретных случайных величин единственным распределением с таким же свойством является геометрическое распределение случайной величины.
ЧАСТЬ 1.
МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
МАССОВОГО ОБСЛУЖИВАНИЯ
|
|
|

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!