Тригонометрические ряды
Функция  , определенная на неограниченном множестве
, определенная на неограниченном множестве  , называется периодической, если существует число
, называется периодической, если существует число 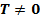 такое, что для каждого
такое, что для каждого  выполняется условие:
выполняется условие:
 , где
, где 
Замечание: Наименьшее из таких чисел  называется периодом функции
называется периодом функции 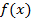 .
.
Примеры
1. Функция  , определенная на интервале
, определенная на интервале  , является периодической, так как существует число
, является периодической, так как существует число  такое, что для всех
такое, что для всех  выполняется условие
выполняется условие 
 Таким образом, функция
Таким образом, функция  имеет период
имеет период  . Аналогично исследуется функция
. Аналогично исследуется функция  .
.
2. Функция  , определенная на множестве
, определенная на множестве  чисел
чисел  является периодической, так как существует число
является периодической, так как существует число  а именно,
а именно,  такое, что для
такое, что для  имеем
имеем 
Функциональный ряд вида


называется тригонометрическим рядом, а постоянные 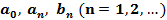 называются коэффициентами тригонометрического ряда (1).
называются коэффициентами тригонометрического ряда (1).
Частичные суммы  тригонометрического ряда (1) являются линейными комбинациями функций из системы функций
тригонометрического ряда (1) являются линейными комбинациями функций из системы функций  которая называется тригонометрической системой. Так как членами этого ряда являются периодические функции с периодом
которая называется тригонометрической системой. Так как членами этого ряда являются периодические функции с периодом 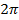 , то в случае сходимости ряда (1) его сумма
, то в случае сходимости ряда (1) его сумма  будет периодической функцией с периодом
будет периодической функцией с периодом  :
:

Разложить периодическую функцию  с периодом
с периодом  в тригонометрический ряд (1) означает найти сходящийся тригонометрический ряд, сумма которого равна функции
в тригонометрический ряд (1) означает найти сходящийся тригонометрический ряд, сумма которого равна функции  .
.
Ортогональность тригонометрической системы
Функции 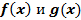 , непрерывные на отрезке
, непрерывные на отрезке  , называются ортогональными на этом отрезке, если выполнено условие
, называются ортогональными на этом отрезке, если выполнено условие

Примеры
Функции  ортогональны на отрезке
ортогональны на отрезке 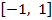 , так как
, так как

Конечная или бесконечная система функций

интегрируемых на отрезке  , называется ортогональной системой на этом же отрезке, если для любых номеров
, называется ортогональной системой на этом же отрезке, если для любых номеров 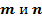 таких, что
таких, что  выполняется равенство
выполняется равенство
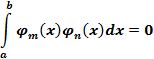
Теорема №1.
Тригонометрическая система
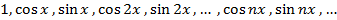
ортогональна на отрезке  .
.
Доказательство
При любом целом  имеем
имеем

С помощью известных формул тригонометрии
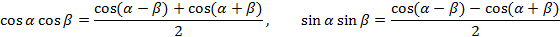
для любых натуральных  находим:
находим:


Наконец, в силу формулы

для любых целых  получаем
получаем

При 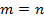 имеем
имеем
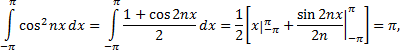


Что и требовалось доказать.
Тригонометрический ряд Фурье
Поставим себе задачей вычислить коэффициенты  тригонометрического ряда (1), зная функцию
тригонометрического ряда (1), зная функцию 
Теорема №2.
Пусть равенство

имеет место для всех значений x, причем ряд в правой части равенства сходится равномерно на отрезке  . Тогда справедливы формулы:
. Тогда справедливы формулы:
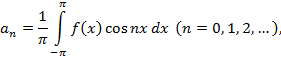

Доказательство
Из равномерной сходимости ряда (1) вытекает непрерывность, а значит, и интегрируемость функции  . Поэтому равенства (2) имеют смысл. Более того, ряд (1) можно почленно интегрировать.
. Поэтому равенства (2) имеют смысл. Более того, ряд (1) можно почленно интегрировать.
Имеем

или

откуда и следует первая из формул (2) для 
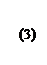 Умножим теперь обе части равенства (1) на функцию
Умножим теперь обе части равенства (1) на функцию 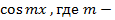 произвольное натуральное число:
произвольное натуральное число:

Ряд (3), как и ряд (1), сходится равномерно. Поэтому его можно интегрировать почленно,

Все интегралы в правой части, кроме одного, который получается при  , равны нулю в силу ортогональности тригонометрической системы. Поэтому
, равны нулю в силу ортогональности тригонометрической системы. Поэтому

откуда

Аналогично, умножая обе части равенства (1) на  и интегрируя от
и интегрируя от  , получим
, получим
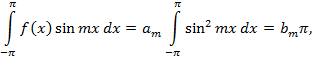
откуда

Что и требовалось доказать.
Пусть дана произвольная периодическая функция  периода 2π, интегрируемая на отрезке
периода 2π, интегрируемая на отрезке  . Можно ли её представить в виде суммы некоторого сходящегося тригонометрического ряда, заранее неизвестно. Однако по формулам (2) можно вычислить постоянные
. Можно ли её представить в виде суммы некоторого сходящегося тригонометрического ряда, заранее неизвестно. Однако по формулам (2) можно вычислить постоянные  и
и  .
.
Тригонометрический ряд

Коэффициенты  которого определяется через функцию
которого определяется через функцию  по формулам
по формулам


Называется тригонометрическим рядом Фурье функции  , а коэффициенты
, а коэффициенты  , определяемые по этим формулам, называются коэффициентами Фурье функции
, определяемые по этим формулам, называются коэффициентами Фурье функции 
Каждой интегрируемой на отрезке  функции
функции  можно поставить в соответствие ее ряд Фурье
можно поставить в соответствие ее ряд Фурье

Т.е. тригонометрический ряд, коэффициенты которого определяются по формулам (2). Однако если от функции  не требовать ничего, кроме интегрируемости на отрезке
не требовать ничего, кроме интегрируемости на отрезке  , то знак соответствия в последнем соотношении, вообще говоря, нельзя заменить знаком равенства.
, то знак соответствия в последнем соотношении, вообще говоря, нельзя заменить знаком равенства.
Замечание. Часто требуется разложить в тригонометрический ряд функцию  , определенную только на отрезке
, определенную только на отрезке  и, следовательно, не являющуюся периодической. Так как в формулах (2) для коэффициентов Фурье интегралы вычисляются по отрезку
и, следовательно, не являющуюся периодической. Так как в формулах (2) для коэффициентов Фурье интегралы вычисляются по отрезку  то такой функции тоже можно написать тригонометрический ряд Фурье. Вместе с тем, если продолжить функцию
то такой функции тоже можно написать тригонометрический ряд Фурье. Вместе с тем, если продолжить функцию  периодически на всю ось Оx, то получим функцию
периодически на всю ось Оx, то получим функцию  на интервале
на интервале  :
:

Эту функцию  называют периодическим продолжением функции
называют периодическим продолжением функции  . При этом функции
. При этом функции  не имеет однозначного определения в точках
не имеет однозначного определения в точках 
Ряд Фурье для функции  тождественен ряду Фурье для функции
тождественен ряду Фурье для функции  . К тому же, если ряд Фурье для функции
. К тому же, если ряд Фурье для функции  с отрезка
с отрезка  на всю ось Ox. В этом смысле говорить о ряде Фурье для функции
на всю ось Ox. В этом смысле говорить о ряде Фурье для функции  , определенной на отрезке
, определенной на отрезке  , равносильно тому, что говорить о ряде Фурье для функции
, равносильно тому, что говорить о ряде Фурье для функции  , являющейся периодическим продолжением функции
, являющейся периодическим продолжением функции  на всю ось Ox. Отсюда следует, что признаки сходимости рядов Фурье достаточно сформулировать для периодических функций.
на всю ось Ox. Отсюда следует, что признаки сходимости рядов Фурье достаточно сформулировать для периодических функций.
Достаточные условия
Примеры
1. Функция  является кусочно-монотонной на интервале
является кусочно-монотонной на интервале  , так как этот интервал можно разбить на два интервала
, так как этот интервал можно разбить на два интервала  , на первом из которых она убывает (и значит, не возрастает), а на втором возрастает (и значит, не убывает).
, на первом из которых она убывает (и значит, не возрастает), а на втором возрастает (и значит, не убывает).
2. Функция  кусочно-монотонна на отрезке
кусочно-монотонна на отрезке  , так как этот отрезок можно разбить на два интервала
, так как этот отрезок можно разбить на два интервала 
Теорема №3
Функция  , кусочно-монотонная и ограниченная на отрезке
, кусочно-монотонная и ограниченная на отрезке  , может иметь на нем только точки разрыва первого рода.
, может иметь на нем только точки разрыва первого рода.
Доказательство


Пусть, например,  точка разрыва функции
точка разрыва функции  Тогда в силу ограниченности функции
Тогда в силу ограниченности функции  и монотонности по обе стороны от точки с существуют конечные односторонние пределы
и монотонности по обе стороны от точки с существуют конечные односторонние пределы

Это означает, что точка c есть точка разрыва первого рода (рис.2). Что и требовалось доказать.
Теорема №4
Если периодическая функция  с периодом 2π кусочно-монотонна и ограничена на отрезке
с периодом 2π кусочно-монотонна и ограничена на отрезке  , то ее ряд Фурье сходится в каждой точке x этого отрезка, причем для суммы
, то ее ряд Фурье сходится в каждой точке x этого отрезка, причем для суммы

Этого ряда выполняются равенства:
1. 
2. 
3. 
Примеры
3. Функция  периода
периода 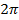 , определенная на интервале
, определенная на интервале  равенством
равенством  , удовлетворяет условиям теоремы. Поэтому её можно разложить в ряд Фурье. Находим для неё коэффициенты Фурье:
, удовлетворяет условиям теоремы. Поэтому её можно разложить в ряд Фурье. Находим для неё коэффициенты Фурье:



Ряд Фурье для такой функции имеет вид

4. Разложить функцию  в ряд Фурье на интервале
в ряд Фурье на интервале 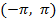 .
.
Данная функция удовлетворяет условиям теоремы 4. Найдем коэффициенты Фурье, используя свойство аддитивности определенного интеграла.



Следовательно, ряд Фурье имеет следующий вид:

На концах отрезка  , т.е. в точках
, т.е. в точках  , которые являются точками разрыва первого рода, будем иметь
, которые являются точками разрыва первого рода, будем иметь  .
.
Замечание. Если в найденном ряде Фурье положить  , то получим
, то получим

Примеры
1. Функция  является четной на отрезке
является четной на отрезке  , так как
, так как 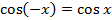 для всех
для всех 
2. Функция  является нечетной на отрезке
является нечетной на отрезке  , так как
, так как  для всех
для всех 
3. Функция  , не принадлежит ни к четным, ни к нечетным функциям, так как
, не принадлежит ни к четным, ни к нечетным функциям, так как
 .
.
Пусть функция  , удовлетворяющая условиям теоремы 1, является четной на отрезке
, удовлетворяющая условиям теоремы 1, является четной на отрезке  . Тогда
. Тогда

т.е.  является четной функцией, а
является четной функцией, а  - нечетной. Поэтому коэффициенты Фурье четной функции
- нечетной. Поэтому коэффициенты Фурье четной функции 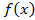 будут равны
будут равны
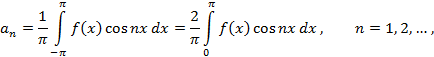

Следовательно, ряд Фурье четной функции имеет вид

Если  нечетная функция на отрезке
нечетная функция на отрезке  , то произведение
, то произведение  будет нечетной функцией, а произведение
будет нечетной функцией, а произведение  четной функцией. Поэтому будем иметь
четной функцией. Поэтому будем иметь
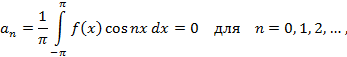

Следовательно, ряд Фурье нечетной функции имеет вид

Примеры
1. Разложить в ряд Фурье на отрезке  функцию
функцию 
>>Решение <<
2. Разложить в ряд Фурье на интервале  функцию
функцию  .
.
>>Решение<<
Примеры
1. Функцию  разложить в ряд Фурье: а) по косинусам; б) по синусам.
разложить в ряд Фурье: а) по косинусам; б) по синусам.
>>> решение <<<
Примеры
1. Разложить в ряд Фурье периодическую функцию с периодом  , заданную на отрезке
, заданную на отрезке  формулой
формулой 
>>Решение и рисунок<<
Теорема №5
Если функция  имеет период
имеет период  и интегрируема, то для любого числа a выполняется равенство
и интегрируема, то для любого числа a выполняется равенство

т.е. интеграл по отрезку, длина которого равная периоду T, имеет одно и то же значение независимо от положения этого отрезка на числовой оси.
Доказательство
В самом деле,

Делаем замену переменной во втором интеграле, полагая  Это дает
Это дает

и следовательно,

Что и требовалось доказать.

 Геометрически это свойство означает, что в случае
Геометрически это свойство означает, что в случае  площади заштрихованных на рис.10 областей равны между собой.
площади заштрихованных на рис.10 областей равны между собой.
Примеры
2. Функция  является периодической с периодом
является периодической с периодом  В силу нечетности данной функции без вычисления интегралов можно утверждать, что при любом a
В силу нечетности данной функции без вычисления интегралов можно утверждать, что при любом a

>>> тут еще замечание должно быть <<<
3. Разложить в ряд Фурье заданную на интервале  функцию
функцию

с периодом 2π.
>> решение <<
Примеры
1. Разложить в комплексный ряд Фурье функцию периода 2π
…. решение….
Ряд Фурье
Введем обозначение
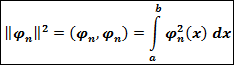
и назовем величину  нормой функции
нормой функции  .
.
Если в ортогональной системе  для всякого n имеем
для всякого n имеем  , то система функций
, то система функций  называется ортонормированной.
называется ортонормированной.
Если система  ортогональна, то система
ортогональна, то система  ортонормирована.
ортонормирована.
Примеры
1.
2.
3.
Система функций  называется ортогональной на интервале
называется ортогональной на интервале  с весом
с весом  , если:
, если:
1. для всех 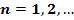 существуют интегралы
существуют интегралы

2.

Здесь предполагается, что весовая функция  определена и положительна всюду на интервале
определена и положительна всюду на интервале  за возможным исключением конечного числа точек, где
за возможным исключением конечного числа точек, где  может обращаться в нуль.
может обращаться в нуль.
Примеры
4.
5.
9.2. Ряд Фурье по ортогональной системе
Пусть  ортогональная система функций в интервале
ортогональная система функций в интервале  и пусть ряд
и пусть ряд

сходится на этом интервале к функции 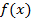 :
:

Умножая обе части последнего равенства на
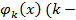
фиксировано) и интегрируя по
x от
a до
b, в силу ортогональности системы

получим, что

или

Эта операция имеет, вообще говоря, чисто формальный характер. Тем не менее, в некоторых случаях, например, когда ряд (4) сходится равномерно, все функции

непрерывны и интервал

конечен, эта операция законна. Но для нас сейчас важна именно формальная трактовка. Итак, пусть задана функция

. Образуем числа

по формуле (5) и напишем

Ряд, стоящий в правой части, называется рядом Фурье функции 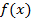 относительно системы
относительно системы  . Числа
. Числа  называются коэффициентами Фурье функции
называются коэффициентами Фурье функции 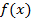 по этой системе. Знак
по этой системе. Знак  в формуле (6) означает лишь, что числа
в формуле (6) означает лишь, что числа  связаны с функцией
связаны с функцией 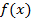 формулой (5) (при этом не предполагается, что ряд справа вообще сходится, а тем более сходится к функции
формулой (5) (при этом не предполагается, что ряд справа вообще сходится, а тем более сходится к функции 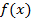 ). Поэтому естественно возникает вопрос: каковы свойства этого ряда? В каком смысле он «представляет» функцию
). Поэтому естественно возникает вопрос: каковы свойства этого ряда? В каком смысле он «представляет» функцию 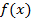 ?
?
Сходимость в среднем
Последовательность  , сходится к элементу
, сходится к элементу  в среднем, если
в среднем, если
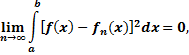
или, что то же,  норма в пространстве
норма в пространстве  .
.
Теорема №6
Если последовательность  сходится равномерно, то она сходится и в среднем.
сходится равномерно, то она сходится и в среднем.
Доказательство
Пусть последовательность  сходится равномерно на отрезке
сходится равномерно на отрезке  к функции
к функции  . Это означает, что для всякого
. Это означает, что для всякого  при всех достаточно больших n имеем
при всех достаточно больших n имеем

Следовательно,

откуда вытекает наше утверждение. Что и требовалось доказать.
Обратное утверждение неверно: последовательность  может сходиться в среднем к
может сходиться в среднем к  , но не быть равномерно сходящейся.
, но не быть равномерно сходящейся.
Пример
Рассмотрим последовательность….
Равенство Парсеваля
Для некоторых систем

знак неравенства в формуле (10) может быть заменен (для всех функций

) знаком равенства. Получаем равенство

называется равенством Парсеваля-Стеклова (условием полноты).
Тождество Бесселя (9) позволяет записать условие (12) в равносильной форме

Тем самым выполнение условия полноты означает, что частичные суммы  ряда Фурье функции
ряда Фурье функции  сходятся к функции
сходятся к функции  в среднем, т.е. по норме пространства
в среднем, т.е. по норме пространства  .
.
Ортонормированная система  называется полной в
называется полной в  , если всякую функцию
, если всякую функцию 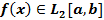 можно с любой точностью приблизить в среднем линейной комбинацией вида
можно с любой точностью приблизить в среднем линейной комбинацией вида

с достаточно большим числом слагаемых, т.е. если для всякой функции 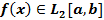 и для любого
и для любого  найдется натуральное число
найдется натуральное число  и числа
и числа  такие, что
такие, что

Теорема №7
Если ортонормированная система  полна в пространстве
полна в пространстве  , то ряд Фурье всякой функции
, то ряд Фурье всякой функции  по этой системе сходится к
по этой системе сходится к  в среднем, т.е. по норме
в среднем, т.е. по норме  .
.
Можно показать, что тригонометрическая система

полна в пространстве  Отсюда следует утверждение.
Отсюда следует утверждение.
Теорема №8
Если функция  , то её тригонометрический ряд Фурье сходится к ней в среднем.
, то её тригонометрический ряд Фурье сходится к ней в среднем.
Упражнения
Разложите в ряд Фурье в интервале  функцию.
функцию.
1. 
2. 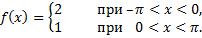
3. 
4. 
5.  .
.
6. 
7. 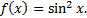
8.  .
.
9. 
10. 
11. 
Разложите в ряд Фурье функцию.
12.  , заданную в интервале
, заданную в интервале  , продолжив её в интервал
, продолжив её в интервал  :
:
a) четным образом;
b) нечетным образом.
13.  , заданную на интервале
, заданную на интервале  .
.
14.  , заданную на интервале
, заданную на интервале  .
.
Разложите в ряд Фурье по синусам функцию.
15. 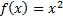 , заданную на интервале
, заданную на интервале  .
.
16.  , заданную на интервале
, заданную на интервале  .
.
Ответы
1.  . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  . 6.
. 6.  . 7.
. 7.  . 8.
. 8.  . 9.
. 9.  . 10.
. 10.  . 11.
. 11.  . 12. а)
. 12. а)  ; б)
; б)  . 13.
. 13.  . 14.
. 14.  . 15.
. 15.  . 16.
. 16.  .
.
Тригонометрические ряды
Функция  , определенная на неограниченном множестве
, определенная на неограниченном множестве  , называется периодической, если существует число
, называется периодической, если существует число 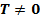 такое, что для каждого
такое, что для каждого  выполняется условие:
выполняется условие:
 , где
, где 
Замечание: Наименьшее из таких чисел  называется периодом функции
называется периодом функции 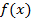 .
.
Примеры
1. Функция  , определенная на интервале
, определенная на интервале  , является периодической, так как существует число
, является периодической, так как существует число  такое, что для всех
такое, что для всех  выполняется условие
выполняется условие 
 Таким образом, функция
Таким образом, функция  имеет период
имеет период  . Аналогично исследуется функция
. Аналогично исследуется функция  .
.
2. Функция  , определенная на множестве
, определенная на множестве  чисел
чисел  является периодической, так как существует число
является периодической, так как существует число  а именно,
а именно,  такое, что для
такое, что для  имеем
имеем 
Функциональный ряд вида


называется тригонометрическим рядом, а постоянные 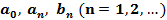 называются коэффициентами тригонометрического ряда (1).
называются коэффициентами тригонометрического ряда (1).
Частичные суммы  тригонометрического ряда (1) являются линейными комбинациями функций из системы функций
тригонометрического ряда (1) являются линейными комбинациями функций из системы функций  которая называется тригонометрической системой. Так как членами этого ряда являются периодические функции с периодом
которая называется тригонометрической системой. Так как членами этого ряда являются периодические функции с периодом 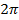 , то в случае сходимости ряда (1) его сумма
, то в случае сходимости ряда (1) его сумма  будет периодической функцией с периодом
будет периодической функцией с периодом  :
:

Разложить периодическую функцию  с периодом
с периодом  в тригонометрический ряд (1) означает найти сходящийся тригонометрический ряд, сумма которого равна функции
в тригонометрический ряд (1) означает найти сходящийся тригонометрический ряд, сумма которого равна функции  .
.
Ортогональность тригонометрической системы
Функции 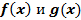 , непрерывные на отрезке
, непрерывные на отрезке  , называются ортогональными на этом отрезке, если выполнено условие
, называются ортогональными на этом отрезке, если выполнено условие

Примеры
Функции  ортогональны на отрезке
ортогональны на отрезке 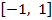 , так как
, так как




 , определенная на неограниченном множестве
, определенная на неограниченном множестве  , называется периодической, если существует число
, называется периодической, если существует число 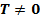 такое, что для каждого
такое, что для каждого  выполняется условие:
выполняется условие: , где
, где 
 называется периодом функции
называется периодом функции 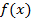 .
. , определенная на интервале
, определенная на интервале  , является периодической, так как существует число
, является периодической, так как существует число  такое, что для всех
такое, что для всех  выполняется условие
выполняется условие 
 Таким образом, функция
Таким образом, функция  имеет период
имеет период  . Аналогично исследуется функция
. Аналогично исследуется функция  .
. , определенная на множестве
, определенная на множестве  чисел
чисел  является периодической, так как существует число
является периодической, так как существует число  а именно,
а именно,  такое, что для
такое, что для  имеем
имеем 


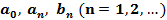 называются коэффициентами тригонометрического ряда (1).
называются коэффициентами тригонометрического ряда (1). тригонометрического ряда (1) являются линейными комбинациями функций из системы функций
тригонометрического ряда (1) являются линейными комбинациями функций из системы функций  которая называется тригонометрической системой. Так как членами этого ряда являются периодические функции с периодом
которая называется тригонометрической системой. Так как членами этого ряда являются периодические функции с периодом 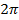 , то в случае сходимости ряда (1) его сумма
, то в случае сходимости ряда (1) его сумма  будет периодической функцией с периодом
будет периодической функцией с периодом 
 в тригонометрический ряд (1) означает найти сходящийся тригонометрический ряд, сумма которого равна функции
в тригонометрический ряд (1) означает найти сходящийся тригонометрический ряд, сумма которого равна функции  , непрерывные на отрезке
, непрерывные на отрезке  , называются ортогональными на этом отрезке, если выполнено условие
, называются ортогональными на этом отрезке, если выполнено условие
 ортогональны на отрезке
ортогональны на отрезке 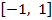 , так как
, так как

 таких, что
таких, что  выполняется равенство
выполняется равенство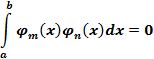
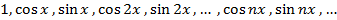
 .
. имеем
имеем
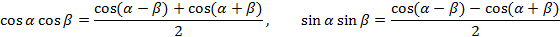
 находим:
находим:


 получаем
получаем
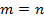 имеем
имеем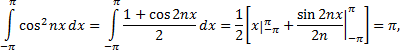


 тригонометрического ряда (1), зная функцию
тригонометрического ряда (1), зная функцию 

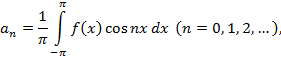

 . Поэтому равенства (2) имеют смысл. Более того, ряд (1) можно почленно интегрировать.
. Поэтому равенства (2) имеют смысл. Более того, ряд (1) можно почленно интегрировать.


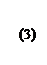 Умножим теперь обе части равенства (1) на функцию
Умножим теперь обе части равенства (1) на функцию 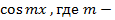 произвольное натуральное число:
произвольное натуральное число:

 , равны нулю в силу ортогональности тригонометрической системы. Поэтому
, равны нулю в силу ортогональности тригонометрической системы. Поэтому

 и интегрируя от
и интегрируя от  , получим
, получим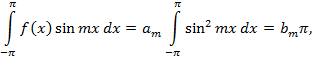

 и
и  .
.
 которого определяется через функцию
которого определяется через функцию  по формулам
по формулам

 , определяемые по этим формулам, называются коэффициентами Фурье функции
, определяемые по этим формулам, называются коэффициентами Фурье функции 

 то такой функции тоже можно написать тригонометрический ряд Фурье. Вместе с тем, если продолжить функцию
то такой функции тоже можно написать тригонометрический ряд Фурье. Вместе с тем, если продолжить функцию  на интервале
на интервале  :
:
 называют периодическим продолжением функции
называют периодическим продолжением функции 
 является кусочно-монотонной на интервале
является кусочно-монотонной на интервале  , так как этот интервал можно разбить на два интервала
, так как этот интервал можно разбить на два интервала  , на первом из которых она убывает (и значит, не возрастает), а на втором возрастает (и значит, не убывает).
, на первом из которых она убывает (и значит, не возрастает), а на втором возрастает (и значит, не убывает). кусочно-монотонна на отрезке
кусочно-монотонна на отрезке 
 , может иметь на нем только точки разрыва первого рода.
, может иметь на нем только точки разрыва первого рода.

 точка разрыва функции
точка разрыва функции 
 , то ее ряд Фурье сходится в каждой точке x этого отрезка, причем для суммы
, то ее ряд Фурье сходится в каждой точке x этого отрезка, причем для суммы



 , удовлетворяет условиям теоремы. Поэтому её можно разложить в ряд Фурье. Находим для неё коэффициенты Фурье:
, удовлетворяет условиям теоремы. Поэтому её можно разложить в ряд Фурье. Находим для неё коэффициенты Фурье:



 в ряд Фурье на интервале
в ряд Фурье на интервале 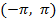 .
.



 , которые являются точками разрыва первого рода, будем иметь
, которые являются точками разрыва первого рода, будем иметь  .
. , то получим
, то получим
 является четной на отрезке
является четной на отрезке 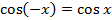 для всех
для всех 
 является нечетной на отрезке
является нечетной на отрезке  для всех
для всех  , не принадлежит ни к четным, ни к нечетным функциям, так как
, не принадлежит ни к четным, ни к нечетным функциям, так как .
. , удовлетворяющая условиям теоремы 1, является четной на отрезке
, удовлетворяющая условиям теоремы 1, является четной на отрезке 
 является четной функцией, а
является четной функцией, а  - нечетной. Поэтому коэффициенты Фурье четной функции
- нечетной. Поэтому коэффициенты Фурье четной функции 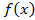 будут равны
будут равны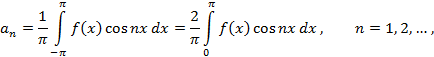


 нечетная функция на отрезке
нечетная функция на отрезке  , то произведение
, то произведение  четной функцией. Поэтому будем иметь
четной функцией. Поэтому будем иметь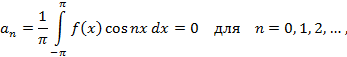



 .
. разложить в ряд Фурье: а) по косинусам; б) по синусам.
разложить в ряд Фурье: а) по косинусам; б) по синусам. , заданную на отрезке
, заданную на отрезке 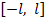 формулой
формулой 


 Это дает
Это дает


 Геометрически это свойство означает, что в случае
Геометрически это свойство означает, что в случае  площади заштрихованных на рис.10 областей равны между собой.
площади заштрихованных на рис.10 областей равны между собой. является периодической с периодом
является периодической с периодом  В силу нечетности данной функции без вычисления интегралов можно утверждать, что при любом a
В силу нечетности данной функции без вычисления интегралов можно утверждать, что при любом a
 функцию
функцию
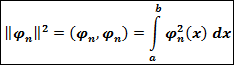
 нормой функции
нормой функции  .
. для всякого n имеем
для всякого n имеем  , то система функций
, то система функций  ортонормирована.
ортонормирована. с весом
с весом  , если:
, если: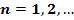 существуют интегралы
существуют интегралы

 ортогональная система функций в интервале
ортогональная система функций в интервале  и пусть ряд
и пусть ряд

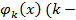 фиксировано) и интегрируя по x от a до b, в силу ортогональности системы
фиксировано) и интегрируя по x от a до b, в силу ортогональности системы  получим, что
получим, что


 непрерывны и интервал
непрерывны и интервал  конечен, эта операция законна. Но для нас сейчас важна именно формальная трактовка. Итак, пусть задана функция
конечен, эта операция законна. Но для нас сейчас важна именно формальная трактовка. Итак, пусть задана функция  . Образуем числа
. Образуем числа  по формуле (5) и напишем
по формуле (5) и напишем

 называются коэффициентами Фурье функции
называются коэффициентами Фурье функции  в формуле (6) означает лишь, что числа
в формуле (6) означает лишь, что числа  , сходится к элементу
, сходится к элементу  в среднем, если
в среднем, если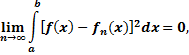
 норма в пространстве
норма в пространстве  .
. сходится равномерно, то она сходится и в среднем.
сходится равномерно, то она сходится и в среднем. при всех достаточно больших n имеем
при всех достаточно больших n имеем

 ) знаком равенства. Получаем равенство
) знаком равенства. Получаем равенство


 .
. , если всякую функцию
, если всякую функцию 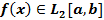 можно с любой точностью приблизить в среднем линейной комбинацией вида
можно с любой точностью приблизить в среднем линейной комбинацией вида
 найдется натуральное число
найдется натуральное число  и числа
и числа  такие, что
такие, что

 Отсюда следует утверждение.
Отсюда следует утверждение. , то её тригонометрический ряд Фурье сходится к ней в среднем.
, то её тригонометрический ряд Фурье сходится к ней в среднем. функцию.
функцию.
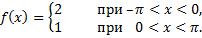


 .
.
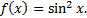
 .
.


 , заданную в интервале
, заданную в интервале  , продолжив её в интервал
, продолжив её в интервал  :
: , заданную на интервале
, заданную на интервале  .
. , заданную на интервале
, заданную на интервале  .
.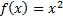 , заданную на интервале
, заданную на интервале  , заданную на интервале
, заданную на интервале  .
. . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  . 6.
. 6.  . 7.
. 7.  . 8.
. 8.  . 9.
. 9.  . 10.
. 10.  . 11.
. 11.  . 12. а)
. 12. а)  ; б)
; б)  . 13.
. 13.  . 14.
. 14.  . 15.
. 15.  . 16.
. 16.  .
.


