Введение
В основе цифрового спектрального анализа лежит аппарат дискретного преобразования Фурье (ДПФ). Однако при использовании ДПФ часто возникают трудности обусловленные конечностью интервала обработки. В настоящей практической работе поставлена цель проанализировать и промоделировать эффекты возникающие при ограничении интервала анализа.
Теоретическая часть
| Рисунок 1: Спектр ограниченного во времени сигнала
|

Пусть имеется сигнал

который бесконечен во времени. В простейшем случае мы можем задать этот сигнал как гармоническое колебание с частотой

. Преобразование Фурье этого сигнала будет представлять собой дельта-импульс на частоте сигнала, т.е.

.
Исходный сигнал и его спектр показаны на рисунке синим цветом. На практике мы не можем произвести расчет спектра путем численного интегрирования по всей оси времени (разумеется, за исключением, когда мы можем получить аналитическое выражение для спектра сигнала, как в приведенном примере), поэтому мы зафиксируем интервал времени  на котором будем рассчитывать спектр сигнала. Таким образом мы получим сигнал
на котором будем рассчитывать спектр сигнала. Таким образом мы получим сигнал  , который совпадает с исходным на интервале времени
, который совпадает с исходным на интервале времени  , но вне интервала наблюдения считаем
, но вне интервала наблюдения считаем  . Математически,
. Математически,  можно представить как произведение исходного бесконечного сигнала
можно представить как произведение исходного бесконечного сигнала  и прямоугольного импульса
и прямоугольного импульса  длительностью
длительностью  ,
,  . Спектр же сигнала
. Спектр же сигнала  , согласно свойствам преобразования Фурье будет равен свертке спектров исходного сигнала и спектра
, согласно свойствам преобразования Фурье будет равен свертке спектров исходного сигнала и спектра  прямоугольного импульса
прямоугольного импульса  :
:

| (1)
|
В выражении (1) было использовано фильтрующее свойство дельта-функции. Сигнал  и его спектр
и его спектр 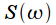 показаны на рисунке 1 красным цветом.
показаны на рисунке 1 красным цветом.
Таким образом, вместо дельта-импульса спектр 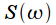 превратился в функцию типа
превратился в функцию типа  , (спектр прямоугольного импульса функции
, (спектр прямоугольного импульса функции  ) причем ширина лепестка зависит от длительности интервала анализа, как это наглядно показано на рисунке 2.
) причем ширина лепестка зависит от длительности интервала анализа, как это наглядно показано на рисунке 2.

Рисунок 2: Изменение спектра с увеличением интервала анализа
Если увеличивать интервал анализа  до бесконечности, то спектр будет сужаться и стремиться к дельта-импульсу. Прямоугольный импульс
до бесконечности, то спектр будет сужаться и стремиться к дельта-импульсу. Прямоугольный импульс  назовем оконной функцией.
назовем оконной функцией.
Практическая часть
Для целей моделирования и исследования взяты следующие оконные функции:
Таблица 1. Выражения для некоторых оконных функций
| Наименование окна
| Выражение в дискретном виде: 
| Примечание
|
| Прямоугольное окно (rectangle window)
| 
| Окно высокого разрешения минимальная ширина главного лепестка, но максимальный уровень боковых лепестков
|
| Синус-окно
| 
| Окно высокого разрешения
|
| Окно Ланцоша (Lanczos window), или sinc - окно
| 
| Окно высокого разрешения
|
| Окно Барлетта (Bartlett window), или треугольное окно
| 
| Окно высокого разрешения
|
| Окно Ханна (Hann window)
| 
| Окно высокого разрешения
|
| Окно Барлетта — Ханна (Bartlett–Hann window)
| 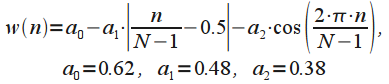
| Окно высокого разрешения
|
| Окно Хемминга (Hamming window)
| 
| Окно высокого разрешения. Наилучшее окно при 
|
| Окно Блэкмана (Blackman window)
| 
| Окно высокого разрешения.
|
| Окно Блэкмана — Харриса (Blackman–Harris window)
| 
| Окно низкого разрешения
|
| Окно Наталла (Nuttall window)
| 
| Окно низкого разрешения
|
| Окно Блэкмана — Наталла (Blackman–Nuttall window)
| 
| Окно низкого разрешения
|
| Окно с плоской вершиной (Flat top window)
| 
| Окно низкого разрешения
|
| Окно Гаусса (Gaussian window)
| 
| Свойства окна зависят от параметра 
|
Схема измерительного стенда

Элемент Windows Type – контроль, позволяющий выбрать идентификатор окна 0 – 14. Где 0 – прямоугольное окно, 1 - Синусоидальное окно, 2 - окно Ланцоша, 3 - окно Барлетта, 4 - окно Ханна, 5 - окно Барлетта-Ханна, 6 - окно Хемминга, 7 – окно Блэкмана, 8 – окно Блэкмана-Харриса, 9 – окно Наталла, 10 – окно Блэкмана-Наталла, 11 – окно с плоской вершиной, 12 – окно Гаусса при параметре 0.3, 13 – то же при параметре 0.5, 14 – то же при параметре 1.2. Элемент Formula Node – генератор сигнала формы окна. Количество отсчетов при генерации выбрано 50. При неверном (несуществующем) выборе устанавливается прямоугольное окно. Генератор формы окна подключен к визуальному интерфейсу Window, предназначенному для визуального контроля формы выбранного окна, и, параллельно, к виджету преобразования Фурье с установленным признаком сдвига и количеством отсчетов равным 500. Для преобразования выхода FFT из массива комплексных чисел в массив реальных чисел выполняется операция взятия модуля, после чего массив спектра поступает на обработку в Formula Node нормализатора спектра, включающего так же логарифмирование. Нормализация спектра производится по 2-м параметрам: нормализация мощности и обрезание динамического диапазона. Первое производится как приведение максимальной амплитуды спектра к 1 путем деления всех элементов спектра на максимальное значение амплитуды до логарифмирования. Второе производится путем принудительной подмены всех значений амплитуды спектра менее 1 мкВ (-120 дБ) на значение -120 дБ. Затем нормализованный спектр выводится на визуальный элемент Spectra.
Результаты измерений, визуальное представление. Прямоугольное окно. Id = 0.

Визуально определяем ∆F0 = 2 (7 мм на экране), ∆F0.5 (-3dB) = 0.86 (3 мм), γ≈ -13 dB, K = 1.
Синус-окно, id = 1

Визуально определяем ∆F0 = 3.1 (11 мм на экране), ∆F0.5 (-3dB) = 1.1 (4 мм), γ≈ -23 dB, K = 1.55.
Окно Ланцоша, id = 2

Визуально определяем ∆F0 = 3.3 (12 мм на экране), ∆F0.5 (-3dB) = 1.3 (5 мм), γ≈ -26,5 dБ, К = 1.65.
Окно Барлетта, id = 3

Визуально определяем ∆F0 = 4 (15 мм на экране), ∆F0.5 (-3dB) = 1.3 (5 мм), γ≈ -26 dB, К = 2.
Окно Ханна, id = 4

Визуально определяем ∆F0 = 4 (15 мм на экране), ∆F0.5 (-3dB) = 1.6 (6 мм), γ≈ -31 dB, К = 2.
Окно Барлета-Ханна, id = 5

Визуально определяем ∆F0 = 4 (15 мм на экране), ∆F0.5 (-3dB) = 1.5 (6 мм), γ≈ -36 dB, К = 2.
Окно Хемминга, id = 6

Визуально определяем ∆F0 = 4 (15 мм на экране), ∆F0.5 (-3dB) = 1.3 (5 мм), γ≈ -42 dB, К = 2.
Окно Блэкмана, id = 7

Визуально определяем ∆F0 = 6 (22 мм на экране), ∆F0.5 (-3dB) = 1.6 (6 мм), γ≈ -58 dB, К = 3.
Окно Блэкмана-Харриса, id = 8

Визуально определяем ∆F0 = 8 (30 мм на экране), ∆F0.5 (-3dB) = 2.1 (8 мм), γ≈ -92 dB, К = 4.
Окно Наталла, id = 9

Визуально определяем ∆F0 = 8 (30 мм на экране), ∆F0.5 (-3dB) = 2.1 (8 мм), γ≈ -93 dB, К = 4.
Окно Блэкмана-Наталла, id = 10

Визуально определяем ∆F0 = 8 (30 мм на экране), ∆F0.5 (-3dB) = 2.1 (8 мм), γ≈ -92 dB, К = 4.
Окно с плоской крышей (flaptop), id = 11

Визуально определяем ∆F0 = 10 (37 мм на экране), ∆F0.5 (-3dB) = 4 (15 мм), γ≈ -68 dB, К = 5.
Гауссово окно (σ = 0.3), id = 12

Визуально определяем ∆F0 = 8 (30 мм на экране), ∆F0.5 (-3dB) = 2 (7 мм), γ≈ -65 dB, К = 4.
Гауссово окно (σ = 0.5), id = 13

Визуально определяем ∆F0 = 3.2 (12 мм на экране), ∆F0.5 (-3dB) = 1.1 (4 мм), γ≈ -32 dB, К = 1.6.
Гауссово окно (σ = 1.2), id = 14

Визуально определяем ∆F0 = 2.3 (8 мм на экране), ∆F0.5 (-3dB) = 1.0 (4 мм), γ≈ -15 dB, К = 1.15.
Выводы
Построенная модель с точностью до результатов измерений виртуальной линейкой на экране монитора, показывает достаточную сходимость полученных результатов с табличными значениями, приведенными в [1]. Первично получена существенная разница в спектрах для окна Ланцоша (ширина лепестка, уровень боковых лепестков – отличаются в 2 раза) и для окна Блэкмана-Наталла (уровень боковых лепестков на 6 дБ хуже табличного значения). Исследование проблемы показало, что реализация функции окна Ланцоша с использованием встроенной функции sinc() дает неверный результат, отличный от реализации через определение sinc как частного sin(pi*x)/(pi*x). Реализация без использования встроенной функции показала сходящийся с эталоном результат. В отношении окна Блэкмана-Наталла причина отличия уровня боковых лепестков частично объясняется тем, что количество отсчетов программы, 50, было взято не по степени двойки. Изменение количества отсчетов программы до 64 улучшает показатель на 2 Дб. Разница в 4 Дб, по видимому, объяснима различием коэффициентов, приведенных в исходном источнике и других работах по оконным функциям.
Литература
[1] http://www.dsplib.ru/content/winadd/win.html
[2] http://diss.vlsu.ru/uploads/media/Dissertacija_Rufov.pdf
[3] https://cfd.spbstu.ru/agarbaruk/doc/Bach_2006_Reznik_Spectra.pdf
Введение
В основе цифрового спектрального анализа лежит аппарат дискретного преобразования Фурье (ДПФ). Однако при использовании ДПФ часто возникают трудности обусловленные конечностью интервала обработки. В настоящей практической работе поставлена цель проанализировать и промоделировать эффекты возникающие при ограничении интервала анализа.
Теоретическая часть
| Рисунок 1: Спектр ограниченного во времени сигнала
|

Пусть имеется сигнал

который бесконечен во времени. В простейшем случае мы можем задать этот сигнал как гармоническое колебание с частотой

. Преобразование Фурье этого сигнала будет представлять собой дельта-импульс на частоте сигнала, т.е.

.
Исходный сигнал и его спектр показаны на рисунке синим цветом. На практике мы не можем произвести расчет спектра путем численного интегрирования по всей оси времени (разумеется, за исключением, когда мы можем получить аналитическое выражение для спектра сигнала, как в приведенном примере), поэтому мы зафиксируем интервал времени  на котором будем рассчитывать спектр сигнала. Таким образом мы получим сигнал
на котором будем рассчитывать спектр сигнала. Таким образом мы получим сигнал  , который совпадает с исходным на интервале времени
, который совпадает с исходным на интервале времени  , но вне интервала наблюдения считаем
, но вне интервала наблюдения считаем  . Математически,
. Математически,  можно представить как произведение исходного бесконечного сигнала
можно представить как произведение исходного бесконечного сигнала  и прямоугольного импульса
и прямоугольного импульса  длительностью
длительностью  ,
,  . Спектр же сигнала
. Спектр же сигнала  , согласно свойствам преобразования Фурье будет равен свертке спектров исходного сигнала и спектра
, согласно свойствам преобразования Фурье будет равен свертке спектров исходного сигнала и спектра  прямоугольного импульса
прямоугольного импульса  :
:

| (1)
|
В выражении (1) было использовано фильтрующее свойство дельта-функции. Сигнал  и его спектр
и его спектр 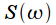 показаны на рисунке 1 красным цветом.
показаны на рисунке 1 красным цветом.
Таким образом, вместо дельта-импульса спектр 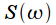 превратился в функцию типа
превратился в функцию типа  , (спектр прямоугольного импульса функции
, (спектр прямоугольного импульса функции  ) причем ширина лепестка зависит от длительности интервала анализа, как это наглядно показано на рисунке 2.
) причем ширина лепестка зависит от длительности интервала анализа, как это наглядно показано на рисунке 2.

Рисунок 2: Изменение спектра с увеличением интервала анализа
Если увеличивать интервал анализа  до бесконечности, то спектр будет сужаться и стремиться к дельта-импульсу. Прямоугольный импульс
до бесконечности, то спектр будет сужаться и стремиться к дельта-импульсу. Прямоугольный импульс  назовем оконной функцией.
назовем оконной функцией.
ДПФ ограниченного во времени сигнала. Использование оконного сглаживания
Теперь рассмотрим случай ДПФ. ДПФ ставит в соответствие  отсчетам сигнала
отсчетам сигнала 
 отсчетов спектра, взятых на одном периоде повторения спектра:
отсчетов спектра, взятых на одном периоде повторения спектра:  Отсчеты сигнала, взятые через равные промежутки времени
Отсчеты сигнала, взятые через равные промежутки времени  где
где  - частота дискретизации (рад/с). Таким образом интервал анализа
- частота дискретизации (рад/с). Таким образом интервал анализа  , тогда спектральные отсчеты берутся через интервал
, тогда спектральные отсчеты берутся через интервал  Ширина главного лепестка спектра
Ширина главного лепестка спектра 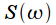 (смотри рисунок 1) равна
(смотри рисунок 1) равна  тогда можно рассмотреть два случая. Первый случай частота сигнала совпадает с
тогда можно рассмотреть два случая. Первый случай частота сигнала совпадает с  -ой частотой спектра
-ой частотой спектра  (верхний график рисунка 3). При дискретизации получим только отсчет на частоте
(верхний график рисунка 3). При дискретизации получим только отсчет на частоте  по амплитуде соответствующий амплитуде сигнала, остальные спектральные отсчеты будут равны нулю, так как моменты дискретизации спектра совпадут с нулями спектра оконной функции. Второй случай когда частота
по амплитуде соответствующий амплитуде сигнала, остальные спектральные отсчеты будут равны нулю, так как моменты дискретизации спектра совпадут с нулями спектра оконной функции. Второй случай когда частота  не совпадает ни с одной частотой из сетки спектральных отсчетов (нижний график рисунка 3). В этом случае спектр сигнала «размывается». Вместо одного спектрального отсчета получаем множество отсчетов, так как дискретизация производится уже не в нулях спектра функции окна, и все боковые лепестки проявляются в спектре. Кроме того амплитуда спектральных отсчетов также уменьшается.
не совпадает ни с одной частотой из сетки спектральных отсчетов (нижний график рисунка 3). В этом случае спектр сигнала «размывается». Вместо одного спектрального отсчета получаем множество отсчетов, так как дискретизация производится уже не в нулях спектра функции окна, и все боковые лепестки проявляются в спектре. Кроме того амплитуда спектральных отсчетов также уменьшается.

Рисунок 3: ДПФ при совпадении и несовпадении частоты сигнала и сетки частот спектра
Совпадение частоты с сеткой спектральных отсчетов будет в том случае если на интервале обработки укладывается целое количество периодов сигнала. В противном случае спектр «размажется».
Размазывание спектра негативный эффект, с которым необходимо бороться. Покажем это на примере. Пусть имеется два гармонических сигнала на частотах  и
и  , причем амплитуда сигнала на частоте
, причем амплитуда сигнала на частоте  много меньше амплитуды сигнала на частоте
много меньше амплитуды сигнала на частоте  . Ограничение интервала анализа приведет к тому, что спектры «размажутся», и сигнал на частоте
. Ограничение интервала анализа приведет к тому, что спектры «размажутся», и сигнал на частоте  будет не заметен под боковым лепестком сигнала с частотой
будет не заметен под боковым лепестком сигнала с частотой  , как это показано на рисунке 4.
, как это показано на рисунке 4.
| Рисунок 4: Сигнал малой амплитуды не заметен под боковым лепестком другого сигнала
|

Очевидно, для того чтобы обнаружить слабый сигнал необходимо устранить боковые лепестки в спектре, которые возникают когда мы ограничили сигнал прямоугольным окном. Значит чтобы устранить эти лепестки необходимо устранить их в спектре оконной функции

, то есть надо изменить оконную функцию, а именно сделать ее более гладкой, как это показано на рисунке 5.
| Рисунок 5 - Гладкая весовая функция
|

При гладкой оконной функции в спектре не наблюдается боковых лепестков (или их уровень существенно понижается), однако имеет место расширение основного лепестка спектра по сравнению с прямоугольным окном

. Таким образом мы вроде бы побороли боковые лепестки, и смогли обнаружить слабые сигналы (рисунок 6), которые раньше терялись в боковых лепестках, но заплатили за это расширением основного лепестка.

Рисунок 6 - При гладкой весовой функции слабые сигналы не теряются в боковых лепестках
Необходимо отметить, что чем больше подавление боковых лепестков спектра оконной функции, тем шире получается основной лепесток. Данное противоречие привело к разработке большого количества оконных функций с различным подавлением боковых лепестков и различной шириной главного лепестка. Основные распространенные окна будут рассмотрены ниже.



 Пусть имеется сигнал
Пусть имеется сигнал  который бесконечен во времени. В простейшем случае мы можем задать этот сигнал как гармоническое колебание с частотой
который бесконечен во времени. В простейшем случае мы можем задать этот сигнал как гармоническое колебание с частотой  . Преобразование Фурье этого сигнала будет представлять собой дельта-импульс на частоте сигнала, т.е.
. Преобразование Фурье этого сигнала будет представлять собой дельта-импульс на частоте сигнала, т.е.  .
.
 на котором будем рассчитывать спектр сигнала. Таким образом мы получим сигнал
на котором будем рассчитывать спектр сигнала. Таким образом мы получим сигнал  , который совпадает с исходным на интервале времени
, который совпадает с исходным на интервале времени  . Математически,
. Математически,  и прямоугольного импульса
и прямоугольного импульса  длительностью
длительностью  . Спектр же сигнала
. Спектр же сигнала  прямоугольного импульса
прямоугольного импульса 
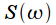 показаны на рисунке 1 красным цветом.
показаны на рисунке 1 красным цветом. , (спектр прямоугольного импульса функции
, (спектр прямоугольного импульса функции 






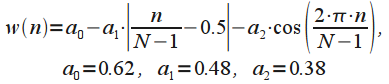

























 отсчетам сигнала
отсчетам сигнала 
 Отсчеты сигнала, взятые через равные промежутки времени
Отсчеты сигнала, взятые через равные промежутки времени  где
где  - частота дискретизации (рад/с). Таким образом интервал анализа
- частота дискретизации (рад/с). Таким образом интервал анализа  , тогда спектральные отсчеты берутся через интервал
, тогда спектральные отсчеты берутся через интервал  Ширина главного лепестка спектра
Ширина главного лепестка спектра  тогда можно рассмотреть два случая. Первый случай частота сигнала совпадает с
тогда можно рассмотреть два случая. Первый случай частота сигнала совпадает с  -ой частотой спектра
-ой частотой спектра  (верхний график рисунка 3). При дискретизации получим только отсчет на частоте
(верхний график рисунка 3). При дискретизации получим только отсчет на частоте 
 , причем амплитуда сигнала на частоте
, причем амплитуда сигнала на частоте  Очевидно, для того чтобы обнаружить слабый сигнал необходимо устранить боковые лепестки в спектре, которые возникают когда мы ограничили сигнал прямоугольным окном. Значит чтобы устранить эти лепестки необходимо устранить их в спектре оконной функции
Очевидно, для того чтобы обнаружить слабый сигнал необходимо устранить боковые лепестки в спектре, которые возникают когда мы ограничили сигнал прямоугольным окном. Значит чтобы устранить эти лепестки необходимо устранить их в спектре оконной функции  При гладкой оконной функции в спектре не наблюдается боковых лепестков (или их уровень существенно понижается), однако имеет место расширение основного лепестка спектра по сравнению с прямоугольным окном
При гладкой оконной функции в спектре не наблюдается боковых лепестков (или их уровень существенно понижается), однако имеет место расширение основного лепестка спектра по сравнению с прямоугольным окном  . Таким образом мы вроде бы побороли боковые лепестки, и смогли обнаружить слабые сигналы (рисунок 6), которые раньше терялись в боковых лепестках, но заплатили за это расширением основного лепестка.
. Таким образом мы вроде бы побороли боковые лепестки, и смогли обнаружить слабые сигналы (рисунок 6), которые раньше терялись в боковых лепестках, но заплатили за это расширением основного лепестка.




