Два узла называются изотопными если от одного к другому можно перейти последовательно выполняя преобразования называться элементарными изотопами.
Элементарные изотопии.
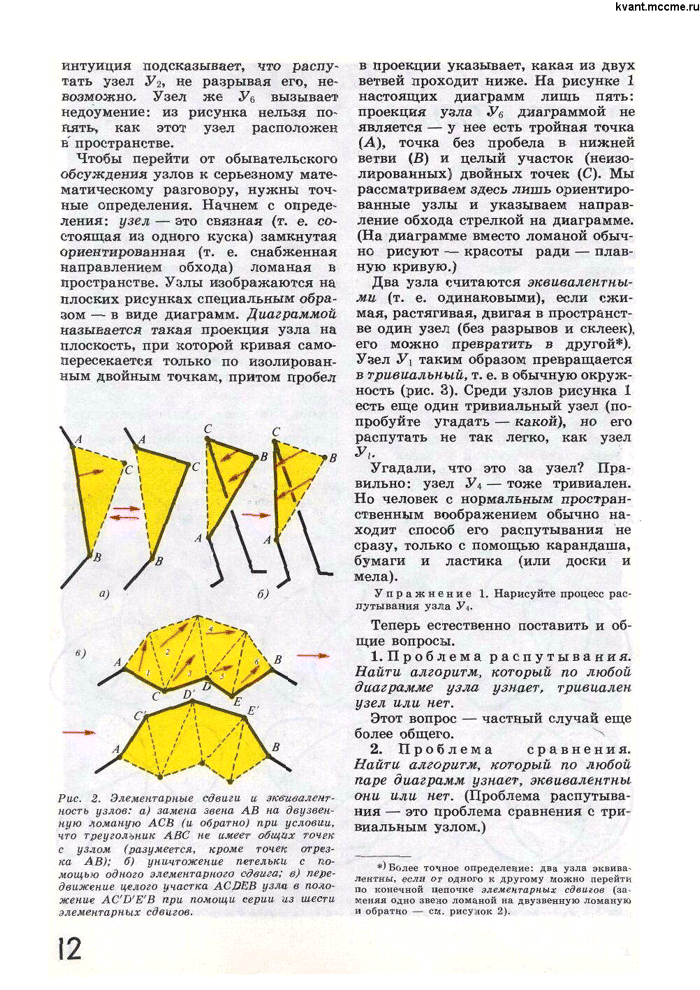
1. Замена одного из звеньев узла двумя новыми отрезками, которые вместе с ним образуют контур треугольника, пересекающегося с прежним узлом только по заменному звену.
2. Замен 2х соседних звеньев одним отрезком, который вместе с ним образует контур треугольника, пересекающихся с прежним узлом только по замененным звеньям.
Проблема распутывания узлов: алгоритм Рейдемейстера.
Проблема распутывания узлов.
Найти алгоритм, который по любой диаграмме узла узнает, тривиален узел или нет. (Проблема распутывания – это это проблема сравнения с тривиальным узлом.)
Операции Рейдемейстера
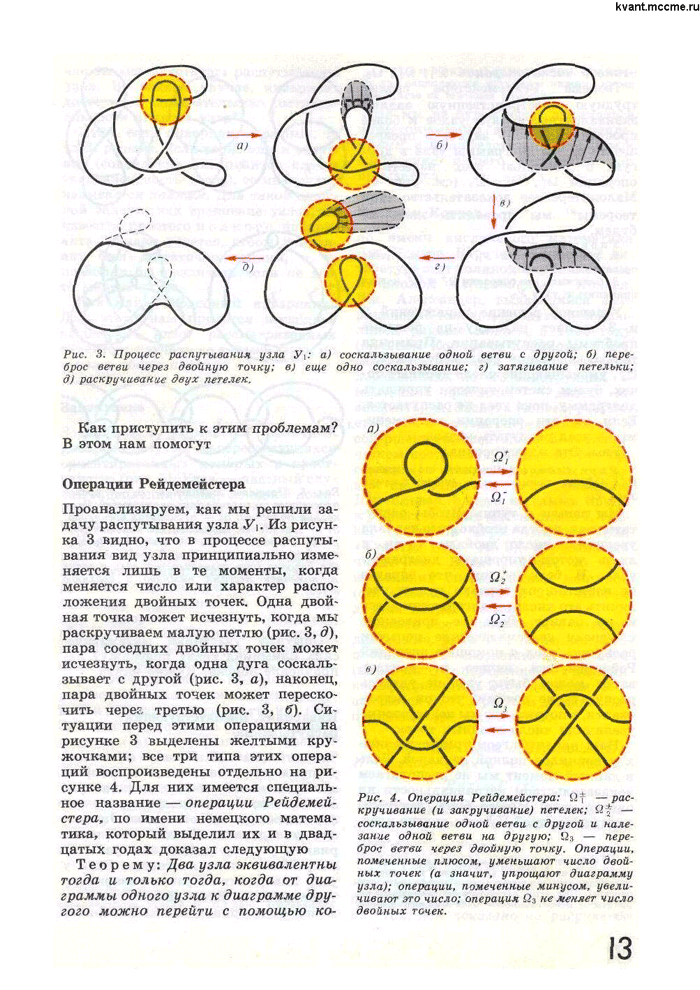
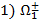 - раскручивание (и закручивание) петелек;
- раскручивание (и закручивание) петелек;
2) 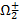 - соскальзывание одной ветви с другой и налезание одной ветви на другую;
- соскальзывание одной ветви с другой и налезание одной ветви на другую;
3) 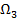 - переброс ветви через двойную точку.
- переброс ветви через двойную точку.
Операции, помеченные плюсом, уменьшают число двойных точек (а значит, упрощают диаграмму узла); операции, помеченные минусом увеличивают это число. Операция 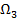 не меняет число двойных точек.
не меняет число двойных точек.
Теорема. Два узла эквивалентны тогда и только тогда, когда от диаграммы одного узла к диаграмме другого можно перейти с помощью конечного числа операций 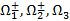 .
.
Теорема Рейдемейстера сводит трудную пространственную задачу эквивалентности двух узлов к более простой «плоской» задаче о превращении одной диаграммы узла в другую с помощью трех известных операций 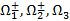 .
.
Этот алгоритм не всегда умеет распутать тривиальные узлы.
Проблема распутывания узлов: алгоритм Ивана Дынникова
Узлы - трехмерные объекты, и почти все из них не удается изобразить на плоскости без перекрещиваний, их нельзя положить на плоскость. Идея Дынникова состоит в том, чтобы использовать не плоскость, а три полуплоскости, то есть «трехстраничную книжку». Обозначим «страницы» этой «книжки» через 𝑃1, 𝑃2 и 𝑃3, а их общую границу – через 𝑙.
Лемма: Для любого узла К существует эквивалентный ему узел 𝐾’, который целиком содержится в объединении полуплоскостей 𝑃1, 𝑃2 и 𝑃3.
Другими словами, любой узел можно уложить на эти три полуплоскости без самопересечений.
Существует 12 типов в поведении узла вблизи точек пересечения в границах полуплоскостей. Они используются для кодировки узла. Существует программа, написанная Дынниковым, которая очень быстро распутывает чрезвычайно сложные узлы. Если же на вход программы подать нетривиальный узел, компьютер будет работать бесконечно долго, честно и тщетно пытаясь выполнить невозможное задание.
Вопрос 29.Проблема распутывания узлов:алгоритм полного перебора с запоминанием.

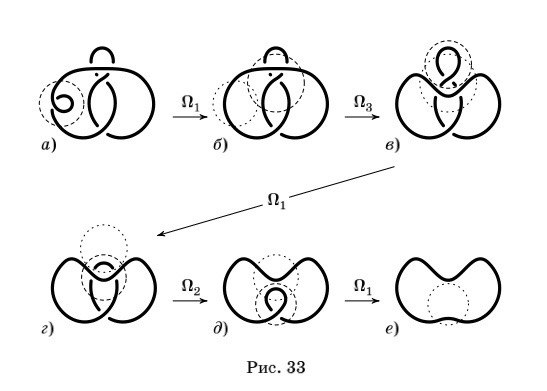
Вопрос 30 Проблема сравнения узлов



Вопрос 31. Инварианты узлов



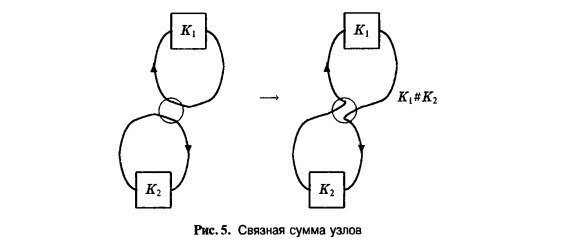
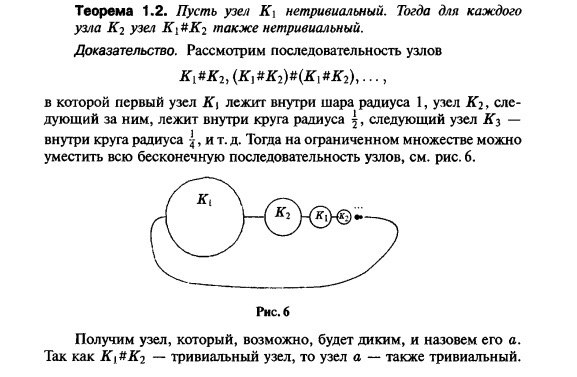
Вопрос 32. Арифметика узлов.



Вопрос. Полином Конвея
Наряду с обычными зацеплениями можно рассматривать ориентированные зацепления, то есть зацепления, на каждой компоненте которых задана ориентация – направление обхода. Для них точно так же определяются плоские диаграммы (с добавлением стрелочек, указывающих ориентацию компонент), а также движения Рейдемейстера (с согласованными ориентациями до и после движения).
Перейдем теперь к построению инвариантов ориентированных зацеплений. Рассмотрим три диаграммы ориентированных зацеплений, которые совпадают в некоторой малой окружности, а внутри нее отличаются так, как показано на рис. 4 сверху. Обозначим такие тройки диаграмм через L , L , L 0.

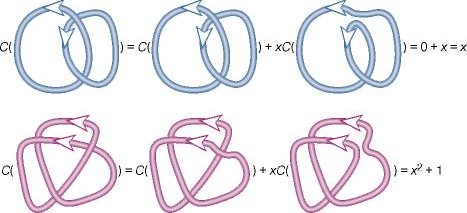
Рис. 4 Вычисление полинома Конвея
Можно показать, что существует единственный инвариант узла C со значениями в полиномах от одной переменной x, равный единице на тривиальном узле, нулю на тривиальном зацеплении из двух или более компоненты для каждой тройки диаграмм соотношению L , L , L 0удовлетворяющий C (L )− C (L ) = C (L 0), называемому соотношением типа Конвея. Такой инвариант называется полиномом Конвея.
Полином Конвея удобен для вычисления. Пусть дана диаграмма L зацепления с n перекрестками. Тогда, изменяя типы некоторых перекрестков (с прохода на переход и наоборот), можно превратить эту диаграмму в тривиальную. Это делается так. Рассмотрим проекцию одной из компонент зацепления и будем прокладывать веревку вдоль нее начиная с некоторой точки. В каждой вершине будем располагать второй виток веревки выше первого (то есть будем класть веревку каждый раз поверх себя). В итоге получим узел, который, очевидно, будет тривиальным. Далее расположим различные компоненты зацепления одна под другой. Получим диаграмму тривиального зацепления. Теперь у нас есть точный алгоритм вычисления полинома Конвея: мы выбираем диаграмму L ' тривиального зацепления, получаемую из диаграммы L заменой некоторых типов перекрестков. Далее мы поочередно изменяем тип перекрестка в каждом из них и записываем соответствующее соотношение типа Конвея (в котором начальная и измененная диаграммы играют роль L +, L -, а роль диаграммы L 0играет диаграмма с n −1перекрестком). В итоге мы получаем, что значение полинома Конвея C (L) равно значению полинома C (L '), то есть нулю или единице в зависимости от числа компонент, плюс сумма значений (со знаками плюс или минус) полинома Конвея на диаграммах с n −1 перекрестком.Таким образом, мы свели вычисление значения полинома Конвея на диаграмме с n перекрестками к вычислению на диаграммах с n −1 перекрестком. Продолжая в этом направлении, мы сведем это вычисление к диаграммам с 0 перекрестков, которые являются тривиальными узлами или зацеплениями.
Проиллюстрируем приведенный алгоритм на зацеплении Хопфа, а затем на правом трилистнике (см.рис. 4 внизу).
К сожалению, на левом трилистнике значение полинома Конвея такжеравно 1 õ 2, то трилистник. Между тем существует много других инвариантов I (гораздо более мощных, чем полином Конвея), равных единице на тривиальном узле и основанных на соотношениях (также называемых соотношениями типа Конвея) вида aI (L +) + bI (L -) = cI (L 0), где a, b, c – некоторые функции от одной или двух переменных. В случае полинома Конвея a = 1, b = −1, c = x. В частности, такие инварианты позволяют отличить левый трилистник от правого. Приведем список наиболее известных из этих инвариантов:
полином Джонса от одной переменной

полином HOMFLY от двух переменных a = x, b = − t, c = 1. Наиболее сильный из этих инвариантов – полином Джонса от двух переменных λ, q, в котором 


Примеры вычисления полинома Конвея.



ИЛИ:





Основные понятия и факты теории кос
Теория кос – это реальная и живая наука, возникшая в 20-ых годах прошлого века тогда еще молодым немецким алгебраистом Э. Артином по заказу ткацкой фабрики: он выполнял, как бы сказали сегодня, хоздоговорную работу для этого предприятия.
Приведем примеры кос (рис. 1).
| К1
| К2
| К3
| К4
|

| 
| 
| 
|
| «Девичья коса»
| Тривиальная коса
| Крашеная коса
| Циклическая коса
|
| Диаграммы – проекция косы на плоскость
|

| 
| 
| 
|
| Рис. 1. Примеры кос из трех и четырех нитей
|
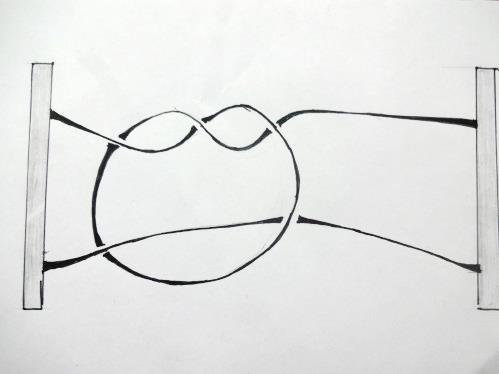
Косу можно себе представлять так: в верхний и нижний край вертикальной доски вбито по n гвоздиков (n может равняться 1, 2, 3, …) – каждый из гвоздиков верхнего основания соединен нитью с одним из гвоздиков нижнего; нити попарно не пересекаются и все время должны опускаться вниз (нить не имеет права, повернувшись, начать подниматься вверх: фигуры на рисунке 2, например, косами не являются).

| 
|
| Рис. 2. Эти фигуры не являются косами: их нити имеют восходящий характер
|
Две косы считаются эквивалентными (т. е. одинаковыми), если одну можно превратить в точную копию другой, двигая нити (без разрывов и склеиваний) так, чтобы каждая точка каждой нити перемещалась только в горизонтальной плоскости. Такое движение показано на рисунке 3.

| 
| 
|
| Рис. 3. Геометрическое доказательство тривиальности косы
|
Коса К тривиальна, ибо она легко превращается (см. рис. 3) в косу из четырех вертикальных нитей).
На рисунке 1 вверху у начала каждой нити указан ее порядковый номер. Внизу снова указан номер каждой нити – но здесь номера не обязаны идти по порядку: каждой косе соответствует перестановка номеров ее нитей. Так, косами К1, К3, К4 на рисунке 1 отвечают перестановки:
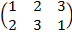 ,
,  ,
,  .
.
Среди кос на рисунке 1 выделяется крашеная коса К3: так она называется вовсе не потому, что нарисовали ее нити разными цветами: крашеной называется любая коса, которой отвечает тождественная перестановка  , т. е. коса, сохраняющая порядок номеров нитей.
, т. е. коса, сохраняющая порядок номеров нитей.
Тривиальная коса, все нити которой вертикальные прямые является частным случаем крашеной косы.
Среди кос следует выделить, кроме крашеных, в известном смысле противоположные им - циклические косы: это косы, переставляющие все номера нитей по единому циклу, как это делает коса К4: 1®2® 4 ®3 ®1.




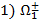 - раскручивание (и закручивание) петелек;
- раскручивание (и закручивание) петелек;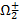 - соскальзывание одной ветви с другой и налезание одной ветви на другую;
- соскальзывание одной ветви с другой и налезание одной ветви на другую;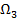 - переброс ветви через двойную точку.
- переброс ветви через двойную точку.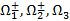 .
.




























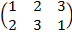 ,
,  ,
,  .
. , т. е. коса, сохраняющая порядок номеров нитей.
, т. е. коса, сохраняющая порядок номеров нитей.

