

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Оснащения врачебно-сестринской бригады.
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Интересное:
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|

| Рис. 8. Сущность сближения меридианов |
Для всех точек, расположенных в восточной половине зоны (по отношению к осевому меридиану зоны), сближение меридианов имеет положительное значение и называется восточным. Для точек, расположенных в западной половине зоны, оно имеет отрицательное значение и называется западным.
Сближение меридианов может быть определено:
- по карте;
- по графику;
- по формуле.
Для определения сближения меридианов по формуле используются геодезические координаты:
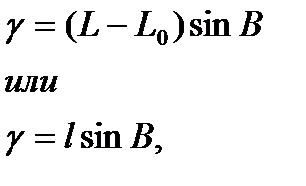 (11)
(11)
где L - долгота заданной точки;
Lo - долгота осевого меридиана зоны, в которой находится заданная точка;
В - широта заданной точки;
l = (L — Lo) - разность долгот.
Знак сближения меридианов зависит от знака разности долгот L — Lo.
Географические (геодезические) координаты В и L, необходимые для вычисления сближения меридианов, определяются по карте с точностью до 0,5'.
Долгота осевого меридиана зоны определяется по формуле:
Lo = 6°N — 3°,
где N - номер координатной зоны, в которой находится заданная точка. Номер координатной зоны определяется по полной ординате у или по формуле:

Единица к частному прибавляется при наличии остатка.
Для определения номера зоны по номенклатуре листа карты необходимо помнить, что нумерация колонн листов карт отличается от номера зоны на 30. При этом, если номер колонны больше 30, то, переходя к номеру зоны, из него вычитают 30, а если меньше тридцати, - то 30 прибавляют. Например, лист карты масштаба 1:50 000 с номенклатурой 0-36-46-Б находится в 6-й зоне (N=36-30=6), а лист карты масштаба 1:100 000 L-4-128 в 34-й зоне (N=4+30=34).
Для определения сближения меридианов по геодезическим координатам формула (11) логарифмируется:
lgγ = Igl + lgsinB.
Пример. Вычислить сближение меридианов для точки с геодезическими координатами: В=56°47,0'; L=28°49,5'.
Решение.
Определяем номер зоны: 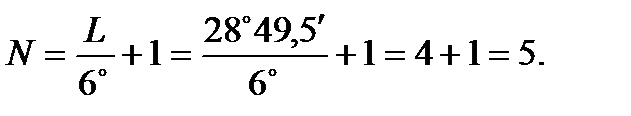
Вычисляем долготу осевого меридиана зоны:
 .
.
Вычисляем разность долгот:

Вычисляем сближение меридианов:
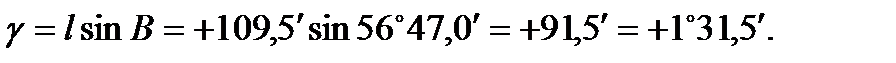
|
|
|

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
© cyberpedia.su 2017-2026 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!