РАСЧЕТ
ПРЯМЫХ СТЕРЖНЕЙ
НА ПРОЧНОСТЬ
Методические указания
по выполнению расчетно-графических работ
Омск - 2001
Составители: С.А.Девятов, З.Н.Соколовский, Е.П.Степанова
Одной из основных задач курсов «Сопротивление материалов» и «Прикладная механика» является приобретение студентами навыков выполнения проектных и проверочных расчетов деталей машин и механизмов на прочность. Для выполнения таких расчетов требуется определять напряжения, возникающие в сечениях стержней под действием внешних нагрузок различного типа. При вычислении напряжений следует оценивать не только характер внешней нагрузки, но и форму поперечного сечения.
Методические указания рекомендуются для студентов механических специальностей. Указания составлены с учетом того, что могут быть использованы студентами заочного отделения.

Комплексная расчетно-графическая работа «Расчет прямых стержней на прочность» имеет целью ознакомление с методами расчета на прочность по допускаемым напряжениям при различных видах напряженного состояния. Для решения задачи необходимо уметь определять геометрические характеристики поперечных сечений, интегральные характеристики напряжений и пользоваться формулами для определения напряжений. Работа включает как задачи по определению размеров поперечного сечения, так и задачи по проверке прочности стержней. В задачи включены также вопросы по исследованию напряженного и деформированного состояния.
Решение задач по определению напряжений и расчета на прочность можно разбить на следующие основные этапы:
1. Определение геометрических характеристик сечений.
2. Определение интегральных характеристик напряжений.
3. Вычисление напряжений и расчет на прочность.
Такое построение расчетно – графической работы позволяет решать задачи поэтапно по мере изложения лекционного материала и проведения практических занятий, что помогает студентам лучше закрепить пройденный материал и рационально использовать время, отведенное для самостоятельной работы.
Рекомендуется для студентов механических специальностей, изучающих курс «Сопротивление материалов» и «Прикладная механика».
Рекомендации по оформлению пояснительной записки
1. Записка оформляется на листах формата А4.
2. Каждая часть задачи делается на отдельном листе, что позволяет выполнять работу в течение семестра.
3. Все решения должны сопровождаться необходимыми пояснениями. Сокращение слов в записке не допускается.
4. На обложке указывается название учебного заведения, наименование кафедры, тема расчетно-графической работы, фамилия студента и учебная группа.
5. Каждую задачу следует начинать с новой страницы с указанием условия и исходных данных.
6. При расчетах следует удерживать не более 3-х значащих цифр.
7. Для всех величин должна быть указана размерность.
8. Все чертежи и графики должны быть выполнены аккуратно в масштабе с указанием необходимых размеров.
9. Схемы нагружения, поперечные сечения стержней и числовые значения выбираются в соответствии с вариантом, выданным преподавателем.
10. Нумерация страниц сквозная от титульного листа до последней страницы.
Краткие сведения из теории
Рис.8
После записи уравнений интегральных характеристик и вычисления начальных параметров можно построить их графики (эпюры). Эти графики строятся на осях, параллельных оси стержня, по нормали к которым откладываются значения функций. Эпюры позволяют наглядно представить изменение интегральных характеристик напряжений вдоль оси стержня и определить то сечение, где функции достигают наибольшего значения.
Обобщенный закон Гука
Напряженное состояние в точке деформированного тела определяется составляющими по трем координатным площадкам sх, sу, sz, txy, txz, tyz. В той же точке деформированное состояние задается составляющими ex, ey, ez,, gху, gyz, gzx, где ex, ey, ez – линейные деформации в данной точке вдоль координатных осей; gху, gyz, gzx – угловые деформации или углы сдвига в координатных плоскостях.
На основании гипотезы об идеальной упругости материала детали связь между этими составляющими описывается следующими выражениями:
ex = [sx - m×(sy +sz)]/E,
ey = [sy - m×(sx + sz)]/E,
ez = [sz - m×(sy + sx)]/E,
gxy = txy/G, gzy = tzy/G, gxz = txz/G.
Эти шесть формул носят название обобщенного закона Гука для изотропного тела в общем случае трехосного напряженного состояния.
Упругие постоянные материала детали:
Е – модуль упругости первого рода или модуль Юнга,
G – модуль упругости второго рода или модуль сдвига,
m - коэффициент Пуассона.
Для стали можно считать
Е = 2×1011 Па; G = 8×1010 Па; m = 0,3.
Решение
Так как материал стержня работает только на растяжение-сжатие, то в точках стержня имеет место одноосное напряженное состояние, и условие прочности можно записать в виде
szmax £ [s] или szmax = Nmax/F £ [s].
Площадь поперечного сечения стержня F = 3pd2/4.
Следовательно, szmax = 4Nmax/ 3pd2 £ [s],
откуда d ³  . (11)
. (11)
Для нахождения наибольшего значения продольной силы Nmax, запишем выражение для этой функции
N(z) = N(0) - q1z + q1(z-l1) - q2(z-l1).
Для заданных условий закрепления на правом конце стержня граничное условие будет
N(l1 + l2) = Р ® N(0) - q1(l1 + l2) + q1l2 - q2l2 = Р,
откуда
N(0) = 50×2-30×1 + 20 = 90 кН.
Окончательно получаем:
N(z) = 90 - 50×z + 50×(z - 2) + 30×(z - 2).
Вычисляем значение продольной силы на границах участков
N(0) =90 кН N(l1) = -10 кН
N(l1) = -10 кН N(l1 + l2) = 20 кН.
По полученным значениям строим эпюру N (рис. 12), из которой видно, что Nmax = 90 кН. Подставляя в формулу (11), получаем
D ³  .
.
Из нормального ряда диаметров принимаем размер d = 20 мм.
q1 q2
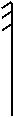





 P
P




N(z)
Рис. 12
П р и м е р 2. По заданной схеме нагружения (рис.13) для стального стержня необходимо:
1. Подобрать диаметр d круглого поперечного сечения из расчета на прочность по теории наибольших касательных напряжений.
2. Вычислить главные линейные деформации в опасной точке стержня.
Рис. 13
Исходные данные:
L = 4 кН×м; m = 8 кН×м/м; l = 1 м; [s] = 160 МПа.
Решение
При кручении в стержнях возникает двухосное напряженное состояние – чистый сдвиг. В точках поперечного сечения, лежащих на контуре, возникают наибольшие касательные напряжения:
tmax = Mк/Wr.
Условие прочности при сложном напряженном состоянии
sэкв £ [s].
По теории наибольших касательных напряжений
sэкв = s1 - s3.
При чистом сдвиге s1 = t, s2 = 0, s3 = -t.
Следовательно
sэкв = s1 - s3 = 2tmax = 2 Mк/Wr.
Для стержня круглого поперечного сечения полярный момент сопротивления Wr = 0,2d3.
Условие прочности примет вид:
sэкв = Mк/0,1d3 £ [s].
Откуда
d ³  .
.
Для определения наибольшего значения крутящего момента необходимо построить график этой функции.
1. Уравнение крутящего момента
Мк(z) = Мк(0) - m(z-l).
На левом конце стержня Мк(0) = L, тогда Мк(z) = 4 – 8(z – 1). Вычисляем значения крутящего момента на границах участка
Мк(0) = 4кН×м,
Мк(l) = 4кН×м,
Мк(2,5l) = -8кН×м
и строим эпюру Мк(z).




 Mk(z)
Mk(z)
Рис. 14
Мкmax = 8кН×м
Подставляя численные значения, находим
d ³  .
.
Принимаем диаметр стержня d = 80 мм.
2.Вычисляем наибольшие касательные напряжения в опасном сечении
tmax = Mкmaх/0,2d3 = 8/0,2×83×10-6 = 78 МПа.
Главные напряжения в опасных точках этого сечения s1 = 78 МПа;
s2 = 0 МПа; s3 = - 78 МПа.
Главные линейные деформации для упругого тела определяем по формулам обобщенного закона Гука, приняв для стали модуль Юнга Е=2×105 МПа, коэффициент Пуассона m=0,3
e1 = [s1 - m(s2 + s3)]/Е = (78 + 0,3×78)/2×106 = 50,7×10-6
e2 = [s2 - m(s3 + s1)]/Е = 0;
e3 = [s3-m(s2 + s1)]/Е = -50,7×106.
Следовательно, и деформированное состояние при кручении будет двухосное.
П р и м е р 3. По заданной схеме нагружения для стержня подобрать двутавровое поперечное сечение из расчета на прочность. Для выбранного стержня построить эпюры нормальных и касательных напряжений и проверить прочность стержня в опасных точках по третьей теории прочности.
Рис.15
Исходные данные: Р = 72 кН, L = 16 кН×м, l = 0,5 м, [s] = 160 МПа.
Решение
Составим уравнение изгибающих моментов Мх и поперечных сил Qy
Qy(z) = Qy(0) + P,
Мх(z) = Мх(0) + QУ(0)z + P(z-l).
Для определения постоянных интегрирования Qy(0) и Мх(0) для заданных условий закрепления концов стержня граничные условия запишутся в следующем виде:
Мх(0) = 0, Мх(2l) = L.
Из второго условия имеем
QУ(0)×2l + Pl = L.
Откуда
QУ(0) = L/2l - P/2 = 16/2×0,5 - 72/2 = -20 кН.
Окончательно получаем
QУ(z) = -20 + 72,
Мх(z) = -20×z + 72(z - 0,5).
Вычисляем значения поперечных сил и изгибающих моментов на границах участков
0 < z < l,
Qy = -20 кН; Мх(0) = 0; Мх(l) = -10 кНм.
l < z < 2l,
Qy = -20 + 72 = 52 кН; Мх(l) = -10 кНм; Мх(2l) = 19 кНм.
По полученным значениям строим эпюры Мх и Qy (рис. 16).
Опасным сечением будет сечение на правой опоре, где Мх = 16 кН×м и Qy = 52 кН.
Условиe прочности при изгибе запишем в виде
sz max = Mx/Wх £ [s].
Откуда
Wх ³ Mx /[s] = 16/160×103 = 100 см3.
Qy(z)
Mx(z)
Рис. 16
По таблицам «Сортамент прокатной стали» выбираем двутавр, имеющий ближайший больший осевой момент сопротивления. Таковым является двутавр №16, имеющий Wх = 109 см3, и осевой момент инерции
Jх = 873 см4.
Построим эпюры нормальных и касательных напряжений по высоте опасного поперечного сечения. Для этого вычислим величины sz и tzy в следующих трех точках сечения:
Точка 1 - крайние точки у = ±h/2.
В этих точках нормальные напряжения достигают наибольшей величины и равны
sz(1) = Mx/Wх= 16/109×10-6 = 147 МПа.
Касательные напряжения в этих точках равны нулю tzy(1) = 0.
Следовательно, в данной точке имеет место одноосное напряженное состояние, и условие прочности в этой точке выполняется.
sz(1) = 147 МПа < [s].
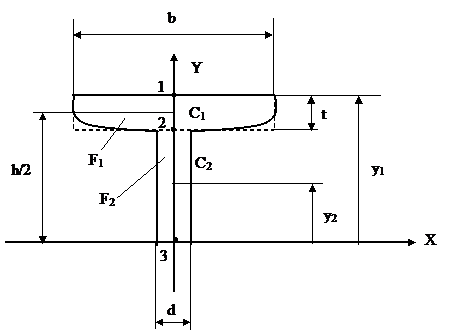
Точка 2 – верхняя точка стенки двутавра (рис.17) с ординатой
у = ±(h/2-t).
Рис.17.
Из таблицы сортаментов выписываем значения размеров двутавра №16: h = 160 мм, b = 81 мм, d = 5 мм, t = 7,8 мм.
Нормальное напряжение в этой точке будет:
sz(2) = Mx(h/2 - t)/Jx = 16(80 – 7,8)/873×10-8 = 132 МПа.
В этой же точке будут возникать касательные напряжения, которые при поперечном изгибе можно определить по формуле Журавского:
tzy=Qy×Sx*/Jx×b(y).
Отсеченной будет одна из частей сечения, если через точку 2 проведем линию, параллельную оси Х. В данном случае удобней взять верхнюю часть, то есть полку двутавра F1. Рассматривая ее как прямоугольник, найдем
Sx*=F1×y1=b×t×(h/2-t/2)=8,1×0,78×(8-0,39)=48,1 cм3.
Ширину сечения в точке 2, не учитывая закругления, примем
b(y) = d = 0,5 см.
Тогда
tzy(2) = 52×48,1×107/873×0,5 = 57 МПа.
Точка 3 - лежит на оси Х.
В этой точке нормальные напряжения равны 0. Отсеченной будет половина поперечного сечения, статический момент ее найдем как сумму статических моментов двух прямоугольников
Sx* = F1×y1 + F2×y2 = b×t×(h/2 - t/2) + (h/2-t) ×d×(h/2 - t)/2 =
= 8,1×0,78(8 - 0,39) + (8 - 0,78) ×0,5(8 - 0,78)/2 = 61 cм3.
Ширина сечения
b(y) = d = 0,5 см.
Касательные напряжения в точке 3
tzy(3) = 52×61×107/873×0,5 = 81 МПа.
По найденным значениям sz и tzy строим их эпюры (рис.18)
sz(y) tzy(y)
Рис. 18
Проверяем условия прочности в этих точках.
Точка 1. sz = 147 МПа и tzy = 0 МПа.
В рассматриваемой точке будет одноосное напряженное состояние, и условие прочности можно записать в виде
sz £ [s].
В данном случае sz =147 МПа < [s], следовательно, условие прочности в точке 1 выполняется.
Точка 2. sz = 132 МПа и tzy = 57 МПа.
В данной точке будет иметь место двухосное напряженное состояние s2 = 0
s1,3 = (sz ±  = (132 ±
= (132 ±  ,
,
s1 = 153 МПа, s3 = -11 МПа.
Условие прочности для сложного напряженного состояния
sэкв £ [s].
По теории наибольших касательных напряжений
sэкв = s1 - s3 = 153 + 11 = 164 МПа.
Эквивалентное напряжение в точке получилось несколько выше допускаемого напряжения, но перегрузка составляет
[(164 - 160)/160]% = 2,5 %,
что лежит в допускаемых пределах.
Точка 3. sz = 0, tzy = 81 МПа.
Такой вид напряженного состояния называется чистым сдвигом. Главные напряжения в т.3 будут равны
s1 = tzy = 81 МПа; s2 = 0; s3 = -tzy = -81 МПа.
Эквивалентное напряжение будет
sэкв = s1 - s3 = 81 + 81 = 162 МПа.
Здесь тоже эквивалентное напряжение оказалось выше допускаемого, но это превышение тоже лежит в допускаемых пределах.
Можно сделать заключение, что условие прочности во всех точках опасного сечения выполняется.
П р и м е р 4. Стержень АВ имеет на правом конце кронштейн ВС, в верхней точке которого приложена горизонтальная сила Р.
Рис. 19
Найти наибольшие напряжения в стержне АВ, если Р = 50 кН,
l = 0,2 м, r = 1 см.
Проверить прочность стержня, приняв допускаемое напряжение
[s] = 200 МПа.
Решение
Приведем силу Р к оси стержня АВ и построим эпюры внутренних сил. При параллельном переносе силы Р из точки С в точку В она приведется к силе Р и паре сил L = Pl.
Уравнения внутренних сил
N(z) = N(0); Qy(z) = Qy(0); Mx(z) = Mx(0) + Qy(0)×z.
Граничные условия
N(0) = 0; Mx(0) = 0; Mx(4l) = L,
откуда Qy(0) = L/4l = P/4.
Окончательно получаем
N(z) = P; Qy(z) = P/4; Mx(z) = P×z/4.
Эпюры внутренних сил приведены на рис.20. 
 N(z)
N(z)

Q
y(z)
M
x(z)
Рис. 20
Таким образом, для стержня АВ вид нагружения будет – растяжение с изгибом. И нормальные напряжения в точках поперечного сечения можно найти по формуле
sz = 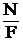 +
+  y
y
Вычислим необходимые геометрические характеристики поперечного сечения стержня АВ (рис.21)

Рис. 21
Сложную фигуру можно представить как составленную из более простых фигур: прямоугольник и два полукруга, для которых известны площади положения центров тяжести и моменты инерции относительно своих центральных осей.
Предварительно определим геометрические характеристики каждой фигуры:
1 фигура – полукруг радиусом r.
Площадь фигуры F1 = pr2/2; осевые центральные моменты инерции Jx1 = 0,1124; Jy = pr4/8, расстояние до центра тяжести У0 = 4r/3p.
2 фигура – прямоугольник с основанием b = 2r и высотой h = 4r.
Площадь фигуры F2 = bh = 8r2.
Центральные осевые моменты инерции
Jx2 = bh3/12 = 2r×(4r)3/12 = 10,7r4; Jy = hb3/12 = 2,67r4.
3 фигура – полукруг радиусом r имеет те же характеристики, что и фигура 1.
Площадь поперечного сечения стержня
F = SFi = F1 + F2 - F3 = F2 = 8r2.
Для определения положения центра тяжести сечения выберем вспомогательные оси ХУ. Ось У является осью симметрии фигуры, и поэтому она будет центральной, а центр тяжести фигуры находится на этой же оси, т.е. абсцисса xс = 0. Ординату центра тяжести найдем по формуле
yc = SSxi/SFi = (S  + S
+ S  + S
+ S 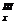 )/F = (F1y1 + F2y2 + F3y3)/F,
)/F = (F1y1 + F2y2 + F3y3)/F,
где y1, y2, y3 – ординаты центров тяжести отдельных фигур относительно оси Х.
Соответственно
y1 = 4r + 4r/3p; y2 = 2r; y3 = 4r/3p.
Теперь
yc = (pr2/2) × (4r + 4r/3p) + 8r2 × 2r - (pr2/2) × 4r/3p = 2,8r.
Проведем через точку С ось Хс, перпендикулярную оси Ус.
Эта ось будет являться не только центральной, но и главной, опять в силу того, что ось Y является осью симметрии. Таким образом, оси ХсYc есть главные центральные оси сечения.
Вычислим главные центральные моменты инерции сечения, используя формулы параллельного переноса осей.
Предварительно найдем расстояния между осью Хс и центральными осями отдельных фигур
a1 = y1 - yc = 4r + 4r/3p - 2,8r = 1,3r;
a2 = -(yc - y2) = -(2,8r - 2r) = -0,8r;
a3 = -(yc - y3) = -(2,8r - 4r/3p) = -2,38r.
Используя формулы параллельного переноса осей, получаем
Jxc = J  + J
+ J  + J
+ J  = (Jx1 + a
= (Jx1 + a  F1) + (Jx2 + a
F1) + (Jx2 + a  F2) - (Jx3 + a
F2) - (Jx3 + a 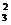 F3) =
F3) =
= 0,11r4 + (1,3)2 × pr2/2 + 10,7r4 + (0,8r)2 × 8r2 - 0,11r4 - (2,38r)2 × pr2/2 =
= 9,36r4 = 9,36 cм4.
Наибольшие параллельные напряжения будут возникать в поперечном сечении стержня В на правой опоре, где
N=P=50 кН, Мх=P×l=10кН×м.
Вычислим напряжения в крайних точках этого сечения.
Крайняя верхняя точка 1: y = 2,2 см.
sz(1) = 50/8 × 104 + 50 × 0,2/9,36 × 2,2 × 106 = 2413 МПа.
Крайняя нижняя точка 2: y = -2,8 см.
sz(2) = 50/8 × 104 + 50 × 0,2/9,36 × (-2,8) × 106 = -2929 МПа.
В обеих точках sz > [s], следовательно, условия прочности не выполняются.
П р и м е р 5. Проверить прочность балки (рис.21), нагруженной поперечными нагрузками, действующими в горизонтальной и вертикальной плоскостях. Стержень изготовлен из швеллера №16 и равнополочного уголка №10с жестко соединенных между собой по всей длине.
Исходные данные: q = 5 кН/м, l = 0,6 м, Рх = Ру = Р = ql = 3 кН,
L = ql2 = 1,8 кНм, [s] = 160 МПа.
Рис. 22
Решение
Выписываем из таблиц прокатного сортамента необходимые данные для фигур, составляющих поперечное сечение:
Швеллер №16: h1 = 16 см, В1 = 6,4 см, F1 = 18,1 см2, Jx1 = 747 см4,
Jy1 = 63,3 см4, z1 = 1,8 см.
Уголок №10: В2 = 10 см, F2 = 15,6 см2, Jx2 = Jy2 = 147 см4, Ju = 233 см4,
Jv = 61 см4, z2 = 2,75 см..
При пользовании таблицами сортамента следует обратить внимание на возможное несовпадение в обозначении осей фигуры, выбранных в задаче и принятых в таблицах. Поэтому все характеристики, взятые из таблиц, необходимо снабдить индексами осей, принятыми в задаче.

 Рис.23
Рис.23
Для определения положения центра тяжести сечения выбираем вспомогательные оси Х1У1, совпадающие с центральными осями швеллера. Вычисляем координаты центра тяжести всего сечения
yc =  см,
см, 
xc =  см.
см. 
Отмеряя по осям Х1У1, соответственно 2,11 см и 2,43 см, находим положение центра тяжести С поперечного сечения стержня. Проводим через эту точку вспомогательные центральные оси ХсУс, параллельные центральным осям швеллера и уголка. Для вычисления центральных осевых и центробежных моментов инерции определим координаты центров тяжести С1 и С2 в системе осей ХсУс:
a1 = -yc = -2,43 см; b1 = -xc = -2,11 см;
a2 = (h1/2 - yc - z2) = (8 - 2,43 - 2,75) = 2,82 см;
b2 = z1 + z2 -xc = 2,75 + 1,6 - 2,11 = 2,44 см.
Используя формулы преобразования, при параллельном переносе осей получаем
Jxc = S(Jxc)i = (Jx1 + a  F1) + (Jx2 + a
F1) + (Jx2 + a  F2) =
F2) =
=(747 + 2,432 × 18,1) + (147 + 2,82 × 15,6) = 1125 см4,
Jyc = S(Jyc)i = (Jy1 + b  F2) + (Jy2 + b
F2) + (Jy2 + b  F2) =
F2) =
= (63,3 + 2,112 × 18,1) + (147 + 2,442 × 15,6) = 384 см4.
Центробежный момент инерции швеллера Jx1y1=0, так как ось Х1 одновременно является осью симметрии. Для уголка главными осями инерции являются оси U и V, повернутые на угол a = 45° по отношению к осям Х2 У2. Для определения центробежного момента относительно этих осей воспользуемся формулами поворота
Jx2y2 = [(Ju - Jv)sin2a]/2 = [(233 - 61)sinp/2]/2=86 см4.
Теперь вычисляем центробежный момент инерции всего сечения относительно центральных осей ХсУ
Jxcyc = Jx1y1 + a1b1F1 + Jx2y2 + a2b2F2 = 0 + (-2,43) × (-2,11) × 18,1 + 86 +
+ 2,82 × 2,44 × 16,6 = 286 cм4.
Вычислим главные моменты инерции по формуле
Jmax,min=0,5[Jxc+Jyc 
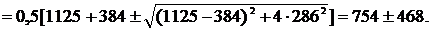
Принимаем Jx0 = Jmax = 1222 см4, Jу0 = Jmin = 287 см4.
Определим положение главных центральных осей Х0У0 по формулам:

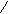
tqa1 = tq(Xc, X0) = (Jxc – Jx0)/Jxcyc = -0,339; a1 = -18,8°.
tqa2 = tq(Yc, Y0) = (Jxc – Jy0)/Jxcyc = 2,93; a2 = 71,2°.
Перейдем к построению эпюр поперечных сил и изгибающих моментов
Qy(z) = Qy(0) – [-P – q(z – 2l)],
Mx(z) = Mx(0) + Qy(0)z – [-P(2 - l) – 0,5q(z – 2l)2].
Граничные условия Qy(3l) = 0; Mx(3l) = 0,
откуда Qy(0) = -P - ql = -3 - 5×0,8 = - 7 кН,
Mx(0) = -Qy(0) × 3l – P – 0,5 × q ×l2 =
=7 × 3 × 0,6 – 0,5 × 5 × 0,82 = 6,3 кН×м.
Окончательно Qy(z) = - 7 + 3 + 5(z - 1,2),
Mx(z) = 6,3 – 7z + 3(z - 0,6) + 0,5(z – 1,2)2.
Вычисляем значения функций на границах участков
0 < Z < l; Qy(0) = -7 кН; Mx(0) = 6,3 кНм,
Qy(l) = -7 кН; Mx(l) = 2,7 кНм.
l < Z < 2l; Qy(l) = -4 кН; Mx(l) = 2,7 кНм;
Qy(2l) = -4 кН; Mx(2l) = 0,9 кНм.
2l < Z < 3l; Qy(2l) = -4 кН; Mx(2l) = 0,9 кНм;
Qy(3l) = 0; Mx(3l) = 0.
В перпендикулярной плоскости
Qx(z) = Qx(0); My(z) = My(0) – Qx(0)z - L
Граничные условия Qx(3l) = P; Mx(3l) = 0.
Откуда Qx(0) = P; Mx(0) = Qx(0)×3l + L = 3 × 1,8 + 1,8 = 7,2 кНм.
Окончательно Qx(z) = 3; Mx(z) = 7,2 – 3z - 1,8.
Поперечная сила постоянна по всей длине стержня и равна 3 кН. Вычислим изгибающий момент на границах участков
0 < Z < l; My(0) = 7,2 кНм; My(l) = 5,4 кНм.
l < Z < 3l; My(l) = 3,6 кНм; Mx(3l) = 0.
По вычисленным значениям строим эпюры (рис. 24).
По полученным эпюрам выбираем опасное сечение стержня. В данном случае таковым будет являться левое концевое сечение (в заделке), так как именно в этом сечении оба изгибающих момента достигают наибольшей величины: Мх = 6,3 кНм, Му = 7,2 кНм. Нормальные напряжения при косом изгибе определяются по формуле:
sz = Mx×y/Jx – My×x/Jy,
где Jx и Jy – главные центральные моменты инерции, т.е. Jx=Jx0=1222 см4, Jx=Jу0=287 см4. Изгибающие моменты должны быть определены тоже относительно главных центральных осей.

Q
y(z)


 Mx(z)
Mx(z)
 Qx(z)
Qx(z)
 My(z)
My(z)
Рис. 24
Поскольку внешние заданные нагрузки действуют в вертикальной и горизонтальной плоскостях, то на рис. 25 имеем эпюры изгибающих моментов, действующих в этих плоскостях, т.е. моменты относительно осей ХсУс. В используемой формуле необходимы моменты относительно главных центральных осей: Мхс = Мх = 6,3 кНм, Му с = Му = 7,2 кНм.

 Yc Y0
Yc Y0



 Myc My0
Myc My0
Mxc




 Xc
Xc
C a°
Mx0
X0
Рис. 25
Найдем требуемые моменты как сумму проекций Мхс, Мус на главные центральные оси сечения
Mx0 = Mxc×cosa0 – Myc×sina0 = 6,3 ×0,947 – 7,2 ×0,323 = 3,64 кНм,
My0 = Myc×cosa0 + Mxc×sina0 = 7,2 ×0,323 + 6,3 ×0,947 = 8,29 кНм.
Следует иметь ввиду, что в данном случае формулы преобразования получены для отрицательного угла a0.
Таким образом, для принятых обозначений осей в решении задачи формулу можно переписать в виде
sz =  y -
y - 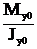 x.
x.
Наибольшие нормальные напряжения будут возникать в точках, наиболее удаленных от нулевой линии. Уравнение нулевой линии в системе главных центральных осей
y0 =  ×x0,
×x0,
где x0, y0 –координаты точек, лежащих на нулевой линии.
y0 = 8,29/3,64 × 1222/287 × x0 =9,7 x0.
Согласно полученному уравнению проводим нулевую линию и находим точки, наиболее удаленные от нее. Это точка А с координатами
xА = -8,7 см, yА = 2,9 см.
Нормальные напряжения в этой точке
sz(A) = [3,64/1222 × 2,9 – 8,29/287 × (-8,7)] × 106 = 259 МПа > [s].
Условие прочности для стержня не выполняется.
П р и м е р 6. Стержень круглого поперечного сечения нагружен горизонтальными и вертикальными нагрузками и крутящим моментом (рис. 26).
Определить диаметр поперечного сечения из расчета на прочность. Исходные данные: Р1 = 6 кН, Р2 = 10 кН, q = 4 кН/м, L = 5 кН×м,
l = 1 м, [s] = 160 МПа.
Рис. 26
Решение
Построение эпюр начнем с рассмотрения сил, действующих в вертикальной плоскости
Qy(z) = Qy(0) + P2,
Mx(z) = Mx(0) + Qy(0) × z + P2 × (z – l).
Граничные условия
Qy(0) = -P1, Mx(0) = 0.
Окончательно получаем:
Qy(z) = -6 + 10, Mx(z) = - 6 × z + 10 × (z – 1).
Под действием сил, действующих в горизонтальной плоскости:
Qx(z) = Qx(0) + q × z – q × (z – 1,5l),
My(z) = My(0) - Qx(0) × z - q × z2/2 + q × (z – 1,5l)2/2.
Соответствующие граничные условия:
Qx(0) = 0, My(0) = 0.
Окончательно получаем:
Qx(z) = 4 × z – 4 × (z – 1,5),
My(z) = - 4 × z2/2 + 4




 . (11)
. (11) .
.










 .
.




 Mk(z)
Mk(z) .
.






 = (132 ±
= (132 ±  ,
,



 N(z)
N(z)
 Qy(z)
Qy(z)

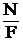 +
+  y
y
 + S
+ S  + S
+ S  )/F = (F1y1 + F2y2 + F3y3)/F,
)/F = (F1y1 + F2y2 + F3y3)/F, + J
+ J  + J
+ J  = (Jx1 + a
= (Jx1 + a  F1) + (Jx2 + a
F1) + (Jx2 + a  F2) - (Jx3 + a
F2) - (Jx3 + a 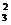 F3) =
F3) =



 Рис.23
Рис.23 см,
см, 
 см.
см. 
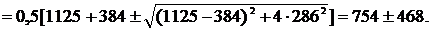

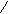


 Qy(z)
Qy(z)




 Mx(z)
Mx(z)
 Qx(z)
Qx(z)
 My(z)
My(z)
 Yc Y0
Yc Y0


 Myc My0
Myc My0




 Xc
Xc y -
y - 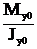 x.
x. ×x0,
×x0,




