

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...
Топ:
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы...
Интересное:
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
АЛГЕБРА
(ЧАСТЬ 1)
Материалы для практических занятий
и самостоятельной работы
для студентов факультета МиИТ
Курган 2013
Кафедра: «Алгебры, геометрии и методики преподавания
математики»
Дисциплины: «Алгебра»
(направления 010100.62 «Математика»; 050100.62)
Составили: канд. физ.-мат. наук О.Н. Шатных.
Утверждены на заседании кафедры «19» ноября 2013 г.
Рекомендованы методическим советом университета
«23» декабря 2013 г.
СОДЕРЖАНИЕ
Введение……………………………………………………………………………...4
Раздел 1 Алгебры………………………………………………………………….…5
Тема 1 Понятие алгебры…………………………………………………………….5
1 Понятие бинарной алгебраической операции…………………………………...5
2 Свойства бинарной алгебраической операции…………………………………..5
3 Виды алгебр. ………………………………………………………………………7
Тема 2 Поле комплексных чисел………………………………………………….10
1 Алгебраическая форма комплексного числа…………………………………...11
2 Геометрическая форма комплексного числа…………………………………...13
3 Тригонометрическая форма комплексного числа……………………………...14
3.1 Умножение и деление комплексных чисел, записанных в тригонометрической форме………………………………………………………..15
3.2 Формула Муавра………………………………………………………………..15
3.3 Извлечение корней n-ой степени из комплексного числа…………………...15
4 Двучленные уравнения…………………………………………………………..17
5 Геометрическое решение уравнений……………………………………………18
Раздел 2 Матрицы и определители……………………………….........................19
Тема 1 Матрицы. Определение матрицы, виды матриц, действия над матрицами.…………………………………………………….……………………19
|
|
Тема 2 Определители. Перестановки из n элементов. Подстановки n-ой степени. Определение определителя n-го порядка. Свойства определителей. Миноры и алгебраические дополнения. Теорема о разложении определителя по элементам строки или столбца. Следствие из неё……………..……………………………...23
Тема 3 Обратная матрица. Вырожденные и невырожденные матрицы. Обратная матрица и ее вычисление. Матричные уравнения……………………………….27
Раздел 3 Системы линейных уравнений. Методы решения систем линейных уравнений…………………………………………………………………………...29
Тема 1 Решение системы n – линейных уравнений с n неизвестными в матричном виде…………………………………………………………………….29
Тема 2 Правило Крамера………..…………………………………………………32
Тема 3 Метод последовательного исключения неизвестных (метод Гаусса).....33
введение
Настоящие материалы составлены в соответствии с программой дисциплины «Алгебра» и предназначены для студентов направлений «Математика» и «Педагогическое образование» профиля «Математическое образование».
Разделы «Алгебры», «Поле комплексных чисел», «Матрицы и определители», «Системы линейных уравнений» изучаются в первом семестре. В данной брошюре представлены все темы раздела, которые выносятся на практические занятия. Для каждой темы указаны основные теоретические положения, приведены образцы решения типовых задач и список задач для решения.
Раздел 1 Алгебры
Тема 1 Понятие алгебры
Понятие бинарной алгебраической операции
Определение. Бинарной алгебраической операцией на множестве М называется правило (закон), по которому любым двум элементам из М, взятым в определенном порядке (т.е. паре (а,b)), ставится в соответствие единственный элемент с из этого же множества.
Пример. 1 Операция сложения на множестве чисел N, Z, Q, R.
2 Операция умножения на множестве чисел N, Z, Q, R.
Задачи для решения
|
|
1 Какие из арифметических действий (сложение, вычитание, умножение, деление) являются бинарными операциями:
а) на множестве {1,0,-1};
б) на множестве N;
в) на множестве Z?
2 Является ли бинарной операцией:
а) умножение на множестве иррациональных чисел;
б) сложение на множестве четных чисел;
в) сложение на множестве нечетных чисел;
г) нахождение десятичных логарифмов на множестве  ;
;
д) нахождение среднего геометрического двух чисел на множестве  ;
;
е) нахождение наибольшего общего делителя на множестве N?
3 Являются ли действия, выполняемые по формулам:
а) a ◦ b = (a + b)²;
б) a ◦ b= 
в) a ◦ b = 
бинарными операциями на множестве Q, и если являются, то почему?
4 Являются ли алгебраической системой множество чисел вида  относительно: а) сложения; б) вычитания; в) умножения?
относительно: а) сложения; б) вычитания; в) умножения?
5 Является ли алгебраической системой множество радиусов-векторов, исходящих из начала декартовой системы координат и расположенных в первой четверти координатной плоскости, с операцией: а) сложение векторов; б) вычитание векторов?
Задачи для решения
1 Являются ли коммутативными и ассоциативными на множестве Z бинарные операции сложения, умножения и вычитания?
2 Докажите, что на множестве  бинарная операция а ◦ b =
бинарная операция а ◦ b =  нахождения среднего геометрического коммутативна, но не ассоциативна.
нахождения среднего геометрического коммутативна, но не ассоциативна.
3 Обладает ли множество чисел вида а + b  , где a и b – любые целые числа, нейтральным элементом относительно обычного умножения? Проверьте, имеются ли в данной алгебраической системе обратные элементы для элементов 2 +
, где a и b – любые целые числа, нейтральным элементом относительно обычного умножения? Проверьте, имеются ли в данной алгебраической системе обратные элементы для элементов 2 +  и 5 - 2
и 5 - 2  . Обратима ли на данном множестве операция умножения?
. Обратима ли на данном множестве операция умножения?
4 Какие из нижеприведенных бинарных операций:
а) a ◦ b =  ;
;
б) a ◦ b = c, где с – наибольший общий делитель чисел а и b;
в) a ◦ b = m, где m – наименьшее общее кратное чисел а и b, коммутативны и какие ассоциативны на множестве N.
5 Покажите, что действие выполняемое по правилу a ◦ b =  , является коммутативной, но не ассоциативной бинарной операцией на множестве R.
, является коммутативной, но не ассоциативной бинарной операцией на множестве R.
6 Докажите, что относительно обычного умножения множество А={x  x=3k, k
x=3k, k 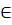 Z} не содержит нейтрального элемента. Обратима ли операция умножения на множестве А?
Z} не содержит нейтрального элемента. Обратима ли операция умножения на множестве А?
7 Пусть I – множество подмножеств некоторого непустого множества М. Существует ли в I нейтральный элемент (если существует, то какой) относительно операции объединения подмножеств на I; пересечения подмножеств? Какие элементы множества I имеют симметричные относительно операций объединения и пересечения? Обратимы ли указанные операции на множестве I?
|
|
8 Докажите, что на множестве Q действие, выполняемое по правилу a◦b = =  является бинарной, коммутативной, ассоциативной, но необратимой операцией. Обладает ли алгебраическая система < Z; ◦ > нейтральным элементом, и если обладает, то каким именно?
является бинарной, коммутативной, ассоциативной, но необратимой операцией. Обладает ли алгебраическая система < Z; ◦ > нейтральным элементом, и если обладает, то каким именно?
Виды алгебр
Определение. Алгеброй называется любое непустое множество А, на котором задана некоторая система операций
S = { 
Обозначается (А, S), где А – множество, S – система операций.
Пример. (N, +), (Q, +, ∙)
Определение. Непустое множество М называется полугруппой, если в нем выполнима одна бинарная алгебраическая операция, которая является ассоциативной.
Пример. (N, +), (Z, ∙).
Определение. Непустое множество G называется группой, если в этом множестве выполнима одна бинарная алгебраическая операция ◦, которая обладает свойствами:
1)  ◦ (b ◦ c) = (
◦ (b ◦ c) = ( ◦ b) ◦ c,
◦ b) ◦ c, 
2)  ◦ e = e ◦
◦ e = e ◦  =
=  ;
;
3)  ◦
◦  ʹ =
ʹ =  ʹ ◦
ʹ ◦  = e.
= e.
Группы по сложению называются аддитивными; группы по умножению – мультипликативными.
Определение. Непустое множество G называется группой, если в этом множестве выполнима одна бинарная алгебраическая операция, которая является ассоциативной и обратимой.
Определение. Если в группе G операция коммутативна, то группа G называется абелевой.
Определение. Непустое множество К называется кольцом, если в нем выполнимы две бинарные алгебраические операции – сложение и умножение, удовлетворяющие условиям:
1) 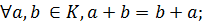
2) 
3) 
4) 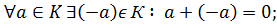
5) 
Примеры колец. При обычных операциях сложения и умножения кольцом является множество целых чисел, множество рациональных чисел, множество действительных чисел.
Определение. Непустое множество Р называется полем, если в нем выполнимы две бинарные алгебраические операции сложение и умножение, удовлетворяющие аксиомам:
1) 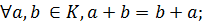
2) 
3) 
4) 
5) 
6) 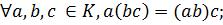
7) 
8) 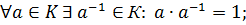
9) 
Пример 1 Доказать, что на множество Z образует группу относительно действия, заданного формулой
 ◦
◦ 
Доказательство
1 Рассматриваемое на Z действие сводится к сложению или вычитанию целых чисел, а т.к. сложение и вычитание элементов из Z дает в результате элемент из Z, то на множестве Z рассматриваемое действие является бинарной операцией.
|
|
2 Проанализируем возможные случаи
a) Если a, b – четные числа, а с – любое число из Z, то
 ◦
◦  ◦
◦ 
 ◦
◦  ) ◦
) ◦ 
т.е.  ◦
◦  ◦
◦  ◦
◦  ) ◦
) ◦  .
.
б) Если a – четное число, b – нечетное, а с – любое число из Z, то
 ◦
◦  ◦
◦ 
 ◦
◦  ) ◦
) ◦ 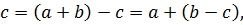
т.е.  ◦
◦  ◦
◦  ◦
◦  ) ◦
) ◦  .
.
в) Если a – нечетное число, b – четное, а с – любое число из Z, то  нечетно и потому
нечетно и потому
 ◦
◦  ◦
◦ 
 ◦
◦  ) ◦
) ◦ 
т.е.  ◦
◦  ◦
◦  ◦
◦  ) ◦
) ◦  .
.
г) Если a, b – нечетные числа, а с – любое число из Z, то  четно и потому
четно и потому
 ◦
◦  ◦
◦ 
 ◦
◦  ) ◦
) ◦ 
т.е.  ◦
◦  ◦
◦  ◦
◦  ) ◦
) ◦  .
.
Итак, во всех возможных случаях заданная на Z бинарная операция является ассоциативной.
3 Т.к. 0 – четное число, то 0 ◦  Кроме того, если
Кроме того, если  , то
, то  ◦ 0 =
◦ 0 =  если же
если же  нечетно, то
нечетно, то  ◦ 0 =
◦ 0 = 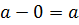 . Итак, 0 ◦
. Итак, 0 ◦ 
 ◦ 0, т.е. 0 является в Z нейтральным элементом относительно заданной операции.
◦ 0, т.е. 0 является в Z нейтральным элементом относительно заданной операции.
4 Для любого элемента  в Z существует обратный элемент: для четного
в Z существует обратный элемент: для четного  обратным будет противоположное число
обратным будет противоположное число  , т.к.
, т.к.  ◦
◦ 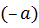 =
=  ; для нечетного
; для нечетного  обратным будет само число
обратным будет само число  , т.к.
, т.к.  ◦
◦  =
=  .
.
Итак, Z является группой относительно заданной операции.
Задачи для решения
1 Является ли множество Z полугруппой относительно: а) сложения, б) вычитания?
2 Является ли множество N полугруппой относительно операции нахождения наибольшего общего делителя?
3 Почему множество R не является полугруппой относительно действия, выполняемого по правилу  ◦ b =
◦ b =  для любых
для любых  , b
, b 
4 Выясните, какие из нижеприведенных множеств являются группами относительно нижеуказанных операций:
а) множество Z относительно вычитания;
б) множество четных чисел относительно умножения;
в) множество целых чисел, кратных любому заданному натуральному числу n, относительно сложения;
г) множество  относительно умножения;
относительно умножения;
д) множество Q относительно умножения;
е) множество Q \ {0} относительно умножения;
ж) множество R \ {0} относительно умножения;
з) множество трехмерных (n-мерных) арифметических векторов относительно сложения;
и) множество чисел вида а + b  относительно сложения, если а и b – любые рациональные числа;
относительно сложения, если а и b – любые рациональные числа;
к) множество многочленов одной и той же степени n от одного аргумента относительно сложения;
л) множество многочленов степени не выше n относительно сложения;
м) множество многочленов от одного аргумента относительно сложения;
5 На множестве Q  {0} определено действие
{0} определено действие  ◦ b =
◦ b =  . Докажите, что относительно указанного действия данное множество является группой.
. Докажите, что относительно указанного действия данное множество является группой.
6 Является ли кольцом множество L чисел вида 
 относительно обычных операций сложения и умножения?
относительно обычных операций сложения и умножения?
7 Докажите, что если на Z задана операция a ʘ b = -ab, то алгебраическая система <Z; +, ʘ> является коммутативным кольцом с единицей. Каков единичный элемент этого кольца?
|
|
8 Докажите, что множество А чисел вида 2а + 2b  где a, b – любые целые числа, является числовым кольцом.
где a, b – любые целые числа, является числовым кольцом.
9 Для каких чисел n = 2, 3, 4, 5, 6, 7 существует поле из n элементов?
10 Почему кольцо {0} не является полем?
11 На множестве М = {a, b} сложение 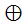 и умножение
и умножение  определены следующим образом:
определены следующим образом:


Выясните, обладает ли это множество нулем и единицей и является ли система <M,  > полем относительно заданных бинарных операций.
> полем относительно заданных бинарных операций.
Задачи для решения
1 Вычислить в алгебраической форме:
а) (3 + 6 i) + (- 3 - 5 i),
б) (- 9 - 4 i) + (- 2 - 3 i),
в) (- 3-i)3,
г) (1 + 6 i) + (1 - 6 i)2 - (4 + i)3 + (- 4 + i),
д) (7 + 4 i)² + 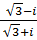 + (5 + i) ∙ (5 - i),
+ (5 + i) ∙ (5 - i),
е) (1+ i)³ + 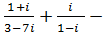 (6 + 4 i) ∙ (- 6 + 4 i),
(6 + 4 i) ∙ (- 6 + 4 i),
ж) 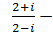 (2 + 3 i) + (5 - 3 i),
(2 + 3 i) + (5 - 3 i),
з)  ,
,
и) 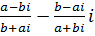 ,
,
к) 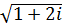 ,
,
л) 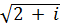 - (9 - i) ∙ (7 + 2 i) ∙ (7 + 3 i) -
- (9 - i) ∙ (7 + 2 i) ∙ (7 + 3 i) - 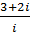 .
.
2 Решить уравнение в действительных числах:
а) (2 x - 5 yi) + (3 y + 2 xi) = 13 - i,
б) 7 (3 x + 2 yi) + (2 y - i) = 19 + 3.
3 Найти z, если:
а) z ∙ (2 + i)=15, б) (2 + 2 i) ∙ z = 8 i.
4 Доказать равенство:
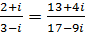 .
.
5 Вычислить:
а) 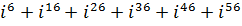 ;
;
б) 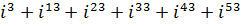 .
.
Задачи для решения
1 Записать комплексные числа, сопряженные данным. Изобразить данные и сопряженные к ним комплексные числа точками на плоскости:
а) 1+ i; б) 4 - 7 i; в) 3;
г) 3 i; д) -1- 3 i; е) 3 + 6 i;
ж) - 3 - 5 i; з) 2 + 3 i; и) - 9 - 4 i; к) 15- i.
Формула Муавра
При любом натуральном n 
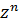 =
=  =
=  ,
,
или
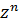 =
= 
– это так называемая формула Муавра позволяющая находить целую степень комплексного числа.
Задачи для решения
1 Записать данные комплексные числа в тригонометрической форме, определив их модули и аргументы:
a) z = 2 + 2 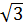 i, б) z =
i, б) z = 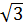 + i,
+ i,
в) z =1- i, г) z = -4,
д) z = 3 i, е) z = -2 i.
ж) z = -10; з) z = 6-6i;
и) z = -1  i; к) z =1
i; к) z =1  i.
i.
2 Найти произведение и частное комплексных чисел  и
и  в тригонометрической форме:
в тригонометрической форме:
а) 
б) 
3 Вычислить:
а)  +
+  б)
б)  ;
;
в)  г)
г) 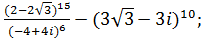
д)  ж)
ж)  ;
;
з) 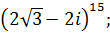 и)
и) 
к)  ; л)
; л)  ;
;
м) 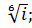 н)
н) 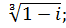
о) 
4 Найти значения  при n = 2, 3, 4, 6.
при n = 2, 3, 4, 6.
Двучленные уравнения
Определение. Уравнения вида  называются двучленными, где
называются двучленными, где 
Решение этого уравнения находится в виде:
 .
.
Решение двучленных уравнений сводится к извлечению корней n-ой степени из комплексных чисел.
Пример Решить уравнение  = 0.
= 0.
Решение
Перепишем уравнение в виде  будем рассматривать
будем рассматривать  32 как комплексное число и представим его в тригонометрической форме:
32 как комплексное число и представим его в тригонометрической форме:
 .
.
Теперь по правилу извлечения корня из комплексного числа найдем

где k следует придать значения 0, 1, 2, 3, 4. Получим пять корней нашего уравнения:


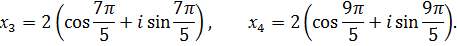
Уравнение имеет один действительный корень и четыре комплексных.
Задачи для решения
1 Решить уравнения:
а)  б)
б) 
в)  г)
г) 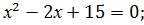
д)  е) 8
е) 8 
ж) 16  з)
з) 
и) -  ; к) 3
; к) 3 
Задачи для решения
1 Найти решение систем:
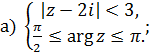
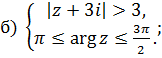
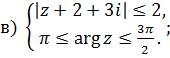
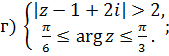
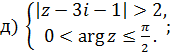
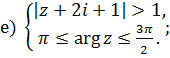
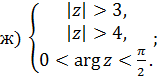
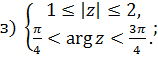
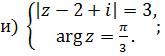
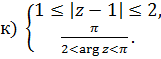
Действия над матрицами
I Суммой матриц A + B называется матрица 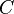 , элементы которой равны суммам соответствующих элементов матриц A и B, т. е. cij = aij + bij.
, элементы которой равны суммам соответствующих элементов матриц A и B, т. е. cij = aij + bij.
Складывать и вычитать можно только матрицы одинаковой размерности (число строк и столбцов у них должно быть одинаково).
Пример 1: 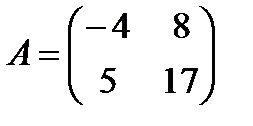 ,
, 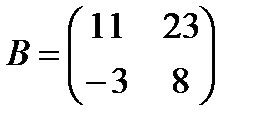 .
.
Решение: 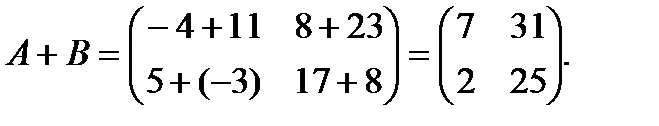
II Произведением матрицы А на число λ называется матрица В, которая получается из матрицы А умножением всех ее элементов на λ, т.е.
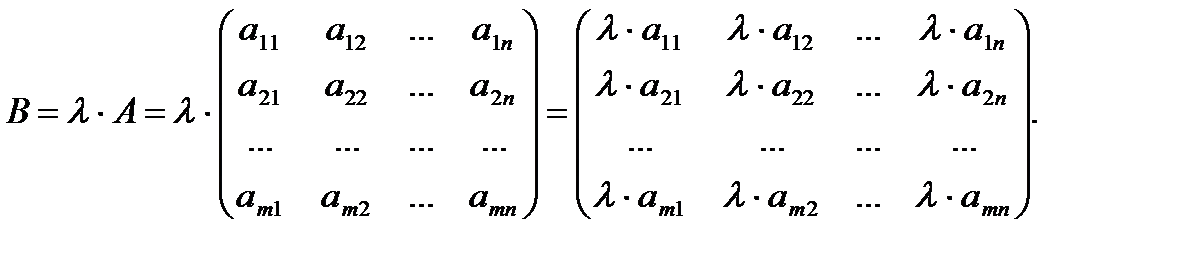
Пример 2: 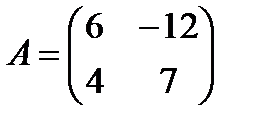 ,
, 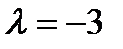 .
.
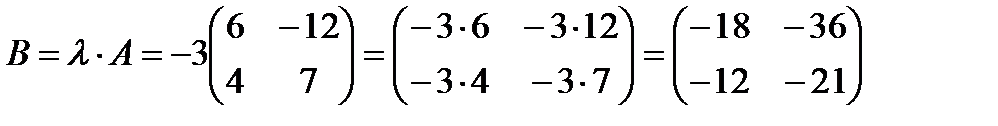 .
.
III Разность двух матриц одинаковой размерности можно определить через операцию сложения матриц и через умножение матрицы на число:
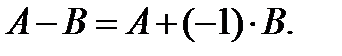
Пример 3: 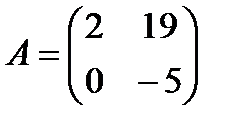 ,
, 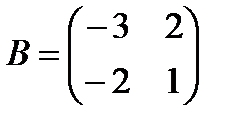 .
.
Решение: 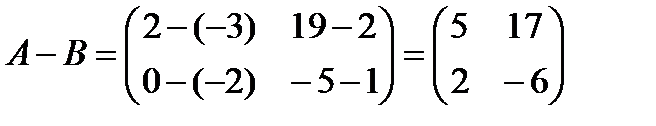 .
.
VI Матрицу 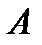 можно умножить на матрицу
можно умножить на матрицу 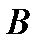 тогда и только тогда, когда число столбцов в первой матрице равно числу строк во второй. При этом получается матрица, имеющая столько строк, сколько в первой, и столько столбцов, сколько во второй.
тогда и только тогда, когда число столбцов в первой матрице равно числу строк во второй. При этом получается матрица, имеющая столько строк, сколько в первой, и столько столбцов, сколько во второй.
Произведением двух матриц 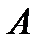 и
и 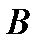 называется матрица
называется матрица 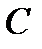 , элементы которой вычисляются по правилу умножения
, элементы которой вычисляются по правилу умножения 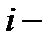 ой строки матрицы
ой строки матрицы 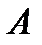 на
на 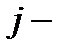 ый столбец матрицы
ый столбец матрицы 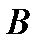 .
.
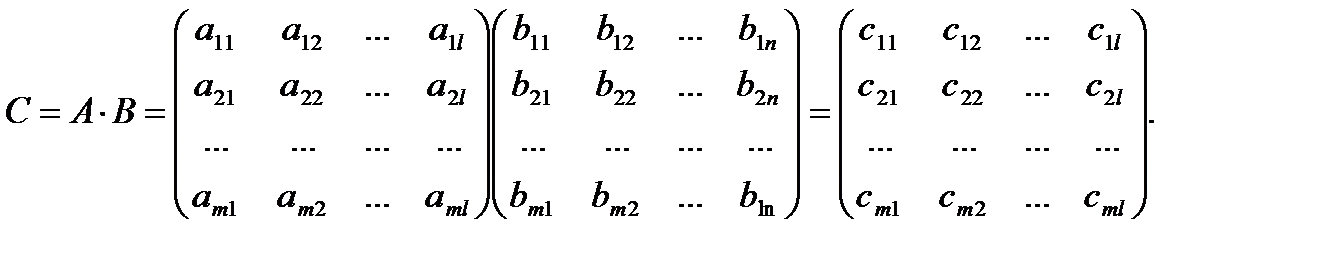
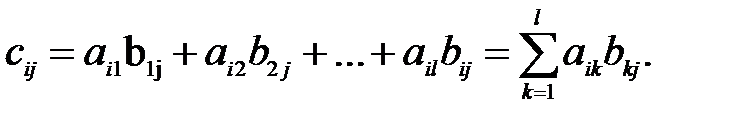
Пример: Умножить матрицу А на матрицу В:
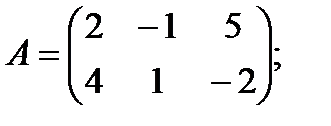
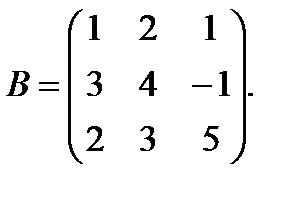
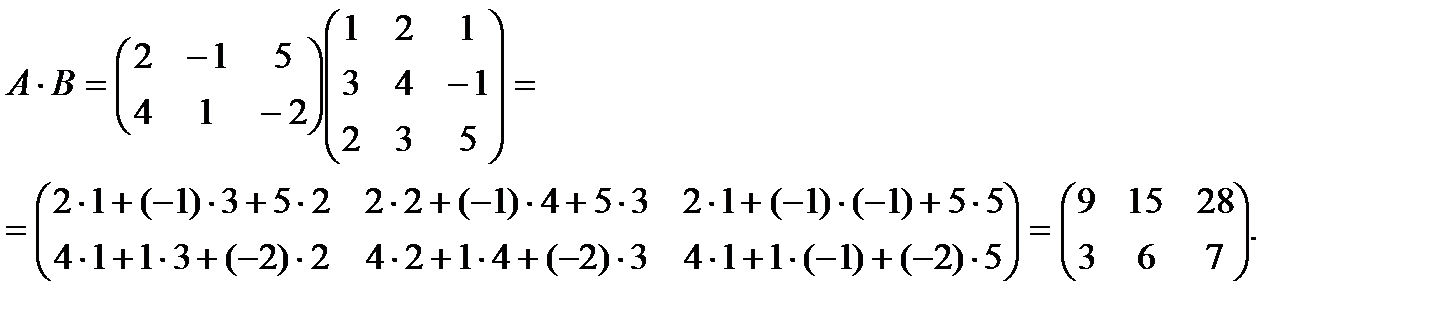
Задачи для решения
1 Найти сумму матриц A и B:
a) 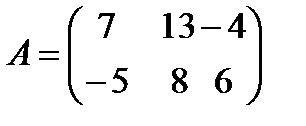 ,
, 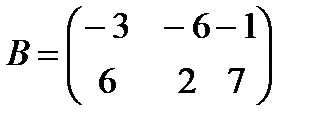 ;
;
б) 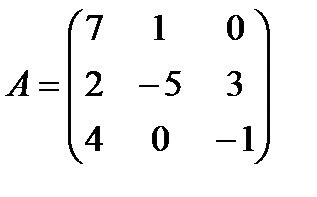 ,
, 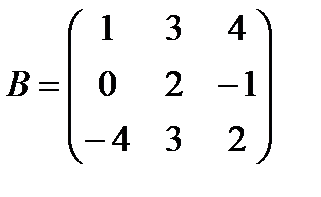 ;
;
в) 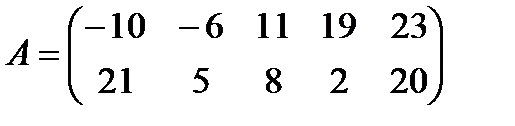 ,
, 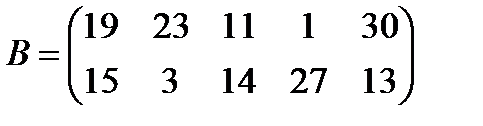 ;
;
г) 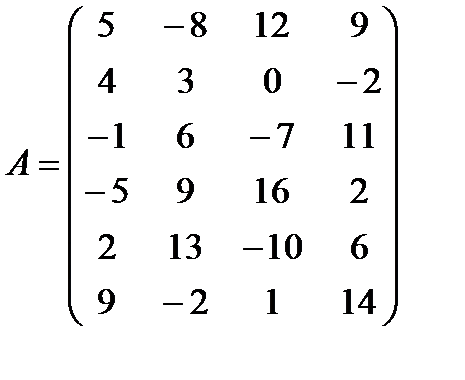 ,
, 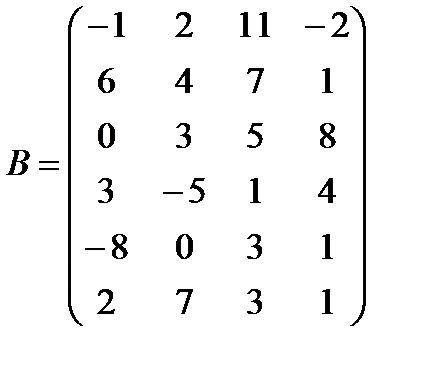 ;
;
д) 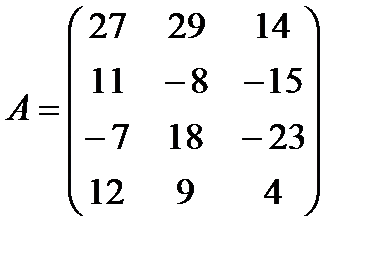 ,
, 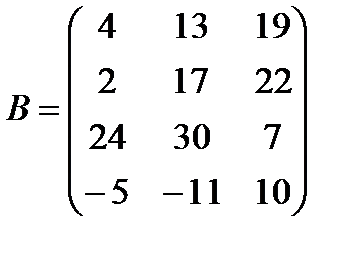 ;
;
е) 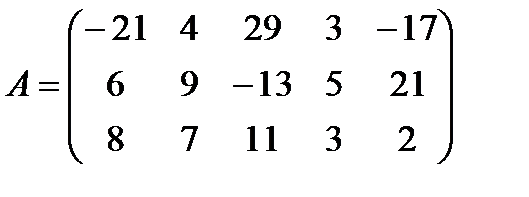 ,
, 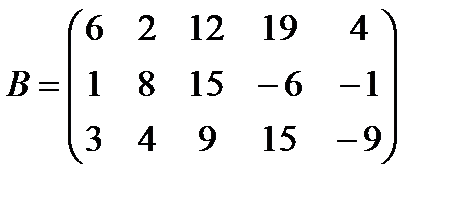 ;
;
2 Умножить матрицу A на число 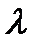 :
:
а) 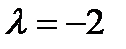 ,
, 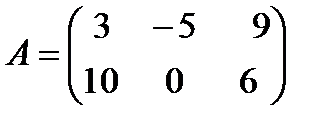 ; б)
; б) 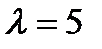 ,
, 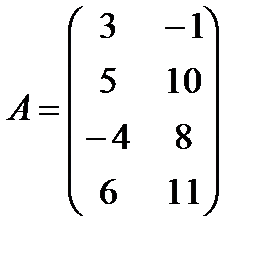 ;
;
в) 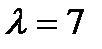 ,
, 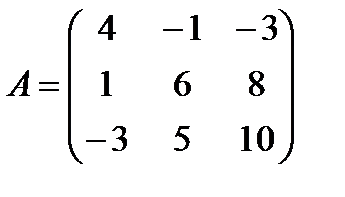 ; г)
; г) 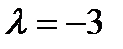 ,
, 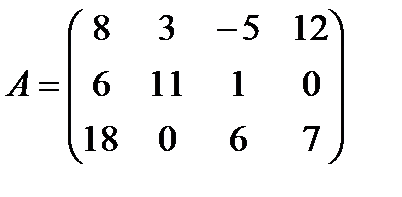 ;
;
д) 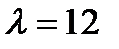 ,
, 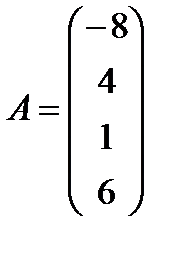 ; е)
; е) 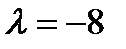 ,
, 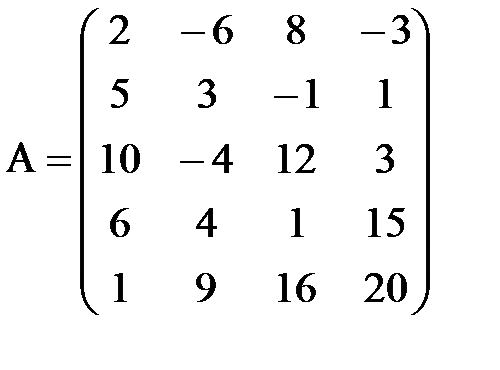 ;
;
3 Найти разность матриц A и B:
a) 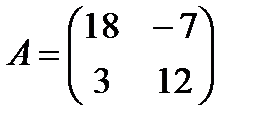 ,
, 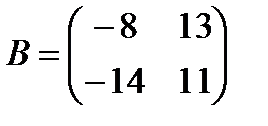 ;
;
б) 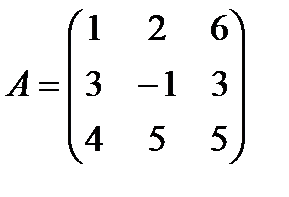 ,
, 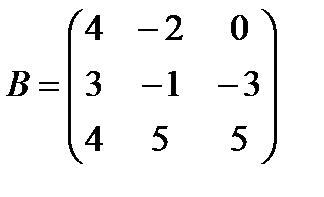 ;
;
в) 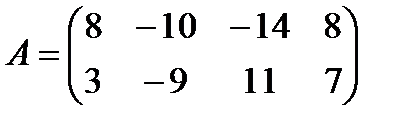 ,
, 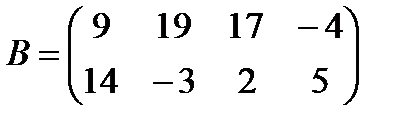 ;
;
г) 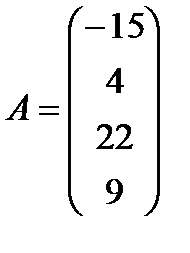 ,
, 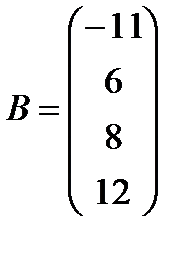 ;
;
д) 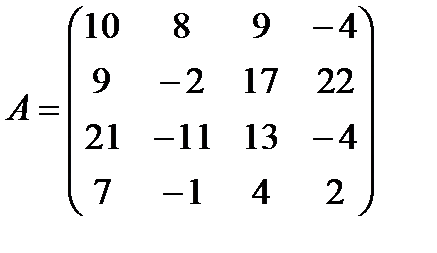 ,
,  ;
;
e) 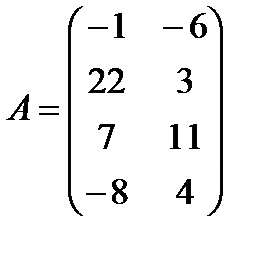 ,
, 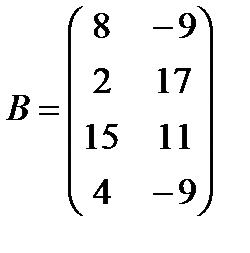 ;
;
4 Найдите произведение матриц A и B:
a) 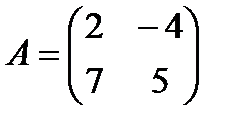 ,
, 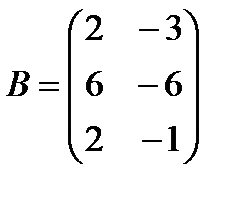 ;
;
б) 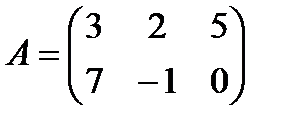 ,
, 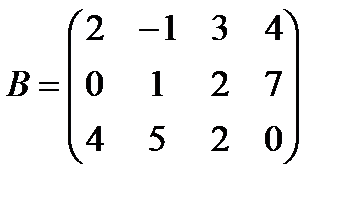 ;
;
в)  ,
, 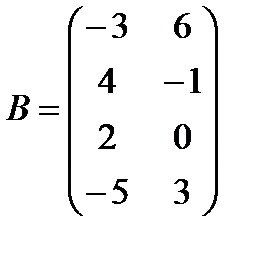 ;
;
г) 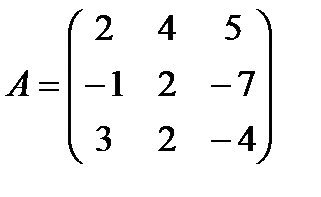 ,
, 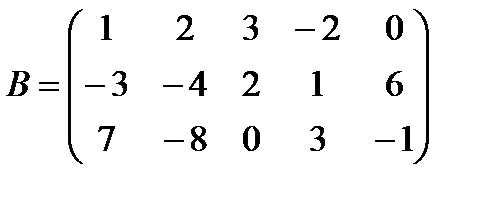 ;
;
д) 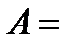
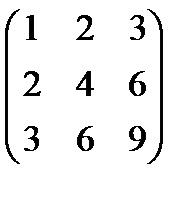 ,
, 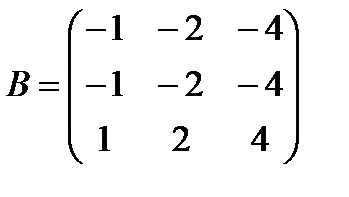 ;
;
е) 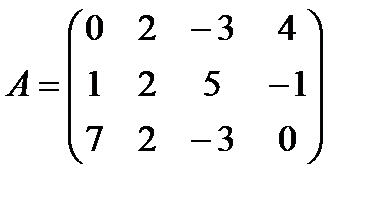 ,
, 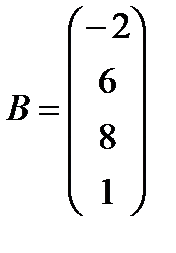 .
.
5 Даны матрицы:
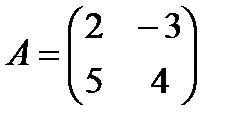 ,
, 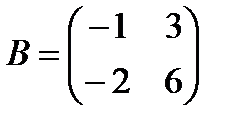 ,
, 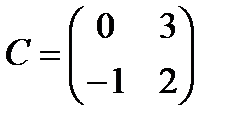
Найти: а) 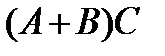 ; б)
; б) 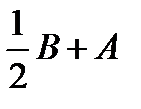 ; в)
; в) 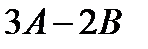 ; г)
; г) 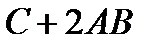 ;
;
д) 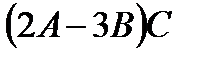 ; е)
; е) 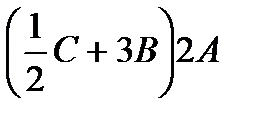 ;
;
6 Выполните действия:
а) 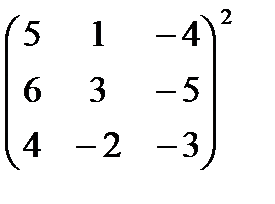 ;
;
б) 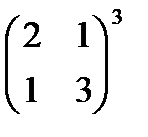 ;
;
в) 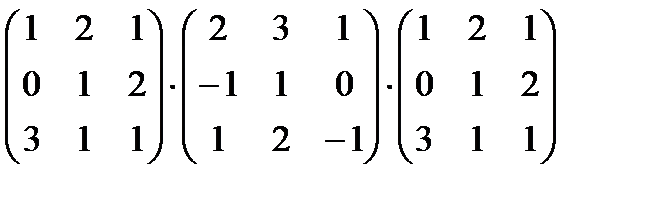 ;
;
г) 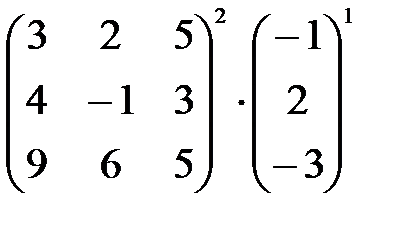 ;
;
д) 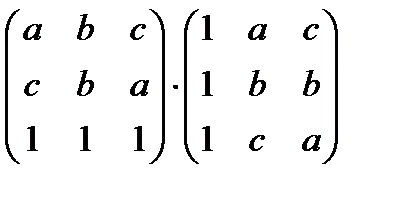 ;
;
е) 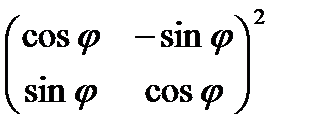 .
.
7 Найти значение многочлена 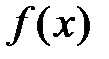 от матрицы А:
от матрицы А:
а) 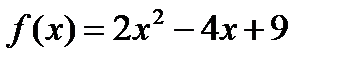 ;
; 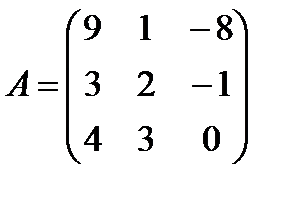 ;
;
б) 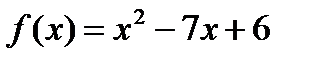 ;
; 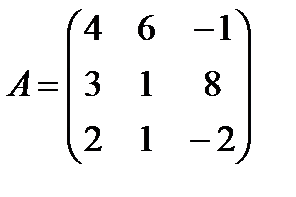 .
.
Тема 2 Определители. Перестановки из n элементов. Подстановки n-ой степени. Определение определителя n-го порядка. Свойства определителей. Миноры и алгебраические дополнения. Теорема о разложении определителя по элементам строки или столбца. Следствие из неё
Перестановкой чисел 1, 2,..., n называется любое расположение этих чисел в определенном порядке. Число всех перестановок, которые можно образовать из n чисел, равно 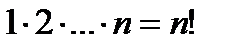 .
.
Если в некоторой перестановке мы поменяем местами какие-либо два символа, а все остальные символы оставим на месте, то мы получим новую перестановку. Это преобразование перестановки называется транспозицией. И нверсию образуют два числа в перестановке, когда меньшее из них расположено правее большего.
Каждой перестановке можно сопоставить число инверсий в ней, которое подсчитывается следующим образом: для каждого из чисел определяют количество стоящих правее его меньших чисел, и полученные результаты складываются.
Перестановка называется четной (или нечетной), если в ней соответственно четно (нечетно) общее число инверсий. Операция, посредством которой от одной перестановки переходят к другой, составленной из тех же n чисел, называется подстановкой n-ой степени.
Произвольное взаимно-однозначное отображение множества первых 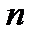 натуральных чисел на себя называется подстановкой
натуральных чисел на себя называется подстановкой 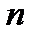 -го порядка. Подстановка может быть записана с помощью двух перестановок.
-го порядка. Подстановка может быть записана с помощью двух перестановок.
Пример перестановки: (1 2 3 4) 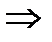 (2 4 1 3);
(2 4 1 3);
Пример транспозиции: (1 2 3 4) 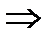 (4 2 3 1);
(4 2 3 1);
Пример инверсии: перестановка (2 4 1 3) содержит три инверсии элементов 2 и 1, 4 и 1, 4 и 3.
Задачи для решения
1 Указать транспозиции, с помощью которых можно
а) от перестановки (10 1 2 8 7 4 3 6 9 5) перейти к перестановке (8 9 5 1 10 7 2 3 6 4)
б) от перестановки (9 5 1 8 3 7 4 6 2) перейти к перестановке (9 8 7 6 5 4 3 2 1)
в) от перестановки (2 4 6 … 2n 1 3 5… 2n-1) перейти к перестановке (2n 2n-1…. 4 3 2 1).
2 Найти число инверсий в следующих перестановках
а)(8 1 5 9 7 4 3 6 2);
б) (10 5 3 8 4 7 2 6 1 9);
в) музыка, если в качестве исходной принимается перестановка букв (а з к м у ы).
Определителем n-го порядка называется алгебраическая сумма n! членов, составленная следующим образом: членами служат всевозможные произведения n элементов матрицы, взятых по одному в каждой строке и в каждом столбце, причем член берется с плюсом, если его индексы составляют четную подстановку, и со знаком минус - в противоположном случае.
Пусть дана квадратная матрица А второго порядка 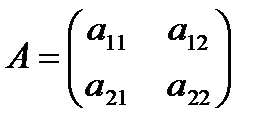 .
.
Определитель квадратной матрицы А второго порядка равен числу 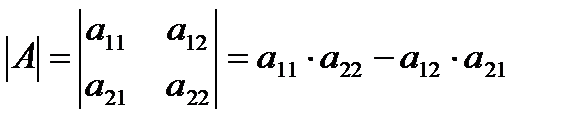 . Диагональ
. Диагональ 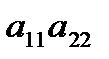 – главная,
– главная, 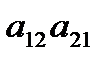 – побочная.
– побочная.
Пусть дана квадратная матрица А третьего порядка 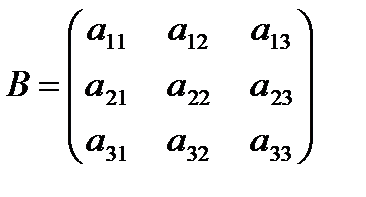 .
.
Определителем квадратной матрицы А третьего порядка называется число, равное
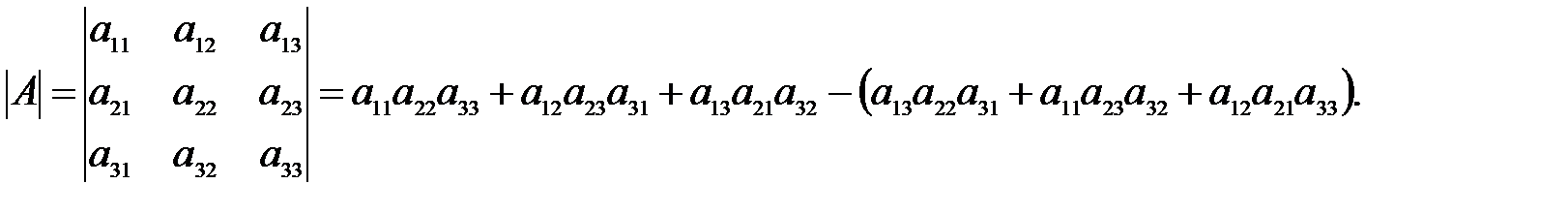
Минором 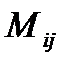 называется определитель, полученный из исходного вычеркиванием
называется определитель, полученный из исходного вычеркиванием 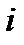 -ой строки и
-ой строки и 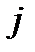 -го столбца.
-го столбца.
Число 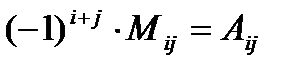 называется алгебраическим дополнением к элементу aij.
называется алгебраическим дополнением к элементу aij.
Теорема 1 (разложение определителя по строке или столбцу):
Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения.
Теорема 2: Сумма произведений элементов некоторой строки квадратной матрицы А на алгебраические дополнения соответствующих элементов другой строки равна нулю.
Теорема 100: Определитель, в котором все элементы одной из строк (столбцов), кроме одного, равны нулю равен произведению этого ненулевого элемента на его алгебраическое дополнение.
Пример 1 Найти определитель матрицы A:
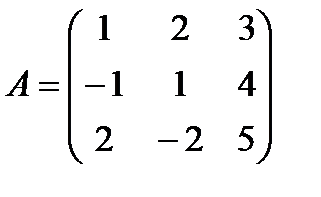
Решение:
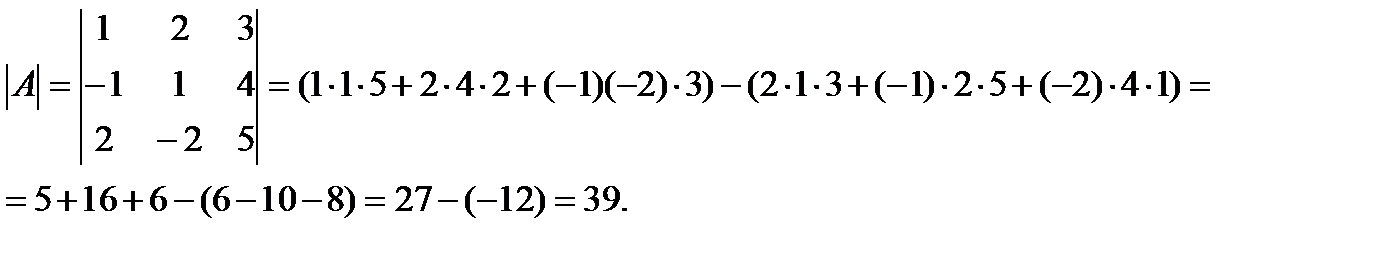
Задачи для решения
1 Найдите определитель 2-го порядка:
а) 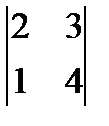 ; б)
; б) 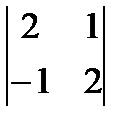 ; в)
; в) 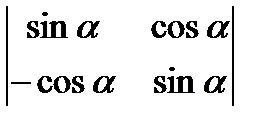 ; г)
; г) 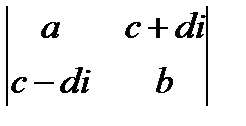 ;
;
д) 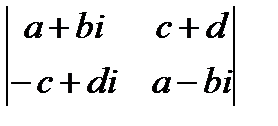 ; е)
; е) 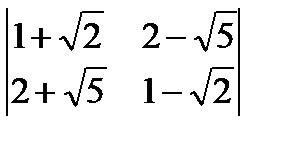 .
.
2 Найдите определитель 3-го порядка:
а) 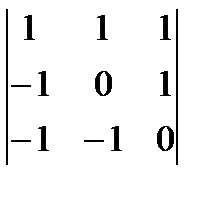 ; б)
; б) 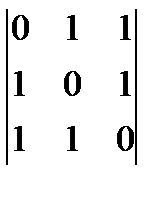 ; в)
; в) 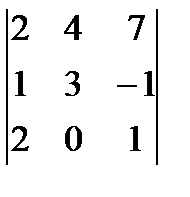 ;
;
г) 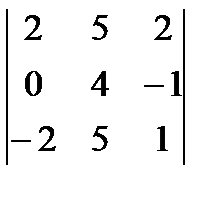 ; д)
; д) 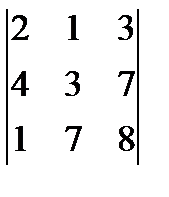 ; е)
; е) 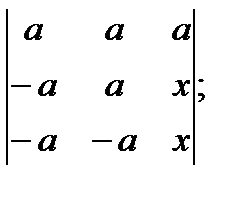
ж) 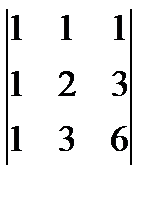 ; з)
; з) 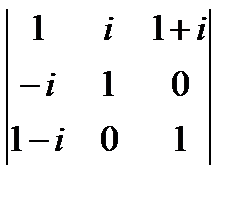 ; и)
; и) 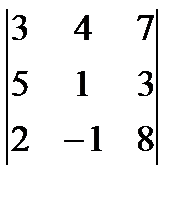 ;
;
к) 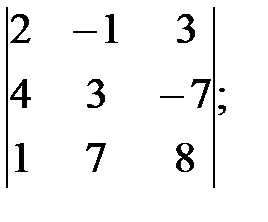 л)
л) 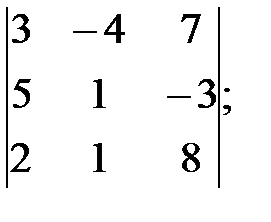 м)
м) 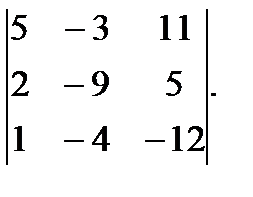
3 Найдите определитель 4-го порядка:
а)

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!