1. Теорема Пуассона (асимптотическая формула для случая малых значений р)
Если вероятность наступления некоторого события А в n независимых испытаниях постоянна и равна р, причем  при
при  так, что
так, что  , где
, где  – среднее число появления события А в n испытаниях,
– среднее число появления события А в n испытаниях,  , то вероятность Pn (m) того, что в этих испытаниях событие А наступит ровно m раз, удовлетворяет при
, то вероятность Pn (m) того, что в этих испытаниях событие А наступит ровно m раз, удовлетворяет при  соотношению (или приближенно равна):
соотношению (или приближенно равна):
Pn (m) = 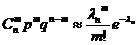 .
.
Замечания.
1. Часто формула Пуассона записывается в виде равенства, но надо помнить при этом, что оно верно при  :
:
Pn (m) =  , при этом
, при этом 
 .
.
2. Формулой пользуются при больших n и малых р. Например, при n > 100,  .
.
3. Теорема имеет место и в том случае, когда вероятность события А в каждом испытании равна нулю. В этом случае  = 0.
= 0.
4. Существуют таблицы значений данной вероятности (стр. 410,411 в задачнике Ефимова – Демидовича).
Пример.
Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двумя и более пулями, если число выстрелов равно 5000.
Решение.
Считаем каждый выстрел за испытание и попадание в цель за событие. Количество испытаний n = 5000 (велико), р = 0,001 (мало). По формуле Бернулли считать сложно. Поэтому применим формулу Пуассона.
Найдем среднее число попаданий: 
 . Найдем заданную вероятность:
. Найдем заданную вероятность:
 (перейдем к противоположному событию: m < 2) =
(перейдем к противоположному событию: m < 2) =  .
.
По точной формуле (формуле Бернулли)  , т.е. ошибка невелика.
, т.е. ошибка невелика.
2. Локальная предельная теорема Муавра - Лапласа (асимптотическая формула для случая больших значений n и m)
Если вероятность наступления некоторого события А в n независимых испытаниях постоянна и равна р, (0 < p < 1), то вероятность Pn (m) того, что в этих испытаниях событие А наступит ровно m раз, удовлетворяет при  соотношению (или приближенно равна):
соотношению (или приближенно равна):
Pn (m) =  ,
,
где  ,
,  .
.
Замечания.
1. Часто формула Пуассона записывается в виде равенства, но надо помнить при этом, что оно верно при  :
:
Pn (m) =  .
.
2. Формулой пользуются при больших n и m. Например, при n > 100,  .
.
3. Из того, что  следует, что
следует, что  . Это означает, что n и m должны отличаться друг от друга не очень сильно. Например, для случая m = 0, теорема дает плохое приближение.
. Это означает, что n и m должны отличаться друг от друга не очень сильно. Например, для случая m = 0, теорема дает плохое приближение.
4. Существуют таблицы значений функции f (x) для положительных значений x (стр. 408 в задачнике Ефимова – Демидовича). Для отрицательных значений x используется та же таблица, так как f (x) – четная функция: f (– x) = f (x). Функцию f (x) называют плотностью нормального распределения.
Пример.
Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.
Решение.
Количество испытаний n = 243, количество успехов m = 70, вероятность успеха р = 0,25, вероятность неудачи q = 1 – 0,25 = 0,75.
По формуле Бернулли считать сложно. Так как n и m велики, поэтому применим формулу Муавра - Лапласа.
Найдем сначала x и f (x):
 , тогда
, тогда  .
.
Можно было не считать значение f (1,37) напрямую, а обратиться к таблице в учебнике.
Подставим найденное значение f (1,37) в формулу:
P 243(70) =  .
.
3. Предельная интегральная теорема Муавра - Лапласа (асимптотическая формула для случая, когда число успехов m лежит в некоторых пределах)
Теорема 1. Если m – число наступлений события А в n независимых испытаниях, в каждом из которых вероятность этого события равна р (0 < p < 1), то равномерно относительно a и b ( ) при
) при  имеет место соотношение:
имеет место соотношение:
 .
.
В некоторых источниках  или
или  .
.
Ранее вывели, что  . Численное значение нашего интеграла можно найти с помощью таблиц (стр. 406 в задачнике Ефимова – Демидовича) для функции Лапласа Ф (x):
. Численное значение нашего интеграла можно найти с помощью таблиц (стр. 406 в задачнике Ефимова – Демидовича) для функции Лапласа Ф (x):
 , где Ф (– x) = 1 – Ф (x). Для тех значений x, которых нет в таблице, т.е для
, где Ф (– x) = 1 – Ф (x). Для тех значений x, которых нет в таблице, т.е для  , Ф (x) = 1.
, Ф (x) = 1.
Либо, функция Лапласа может быть в виде:  , где Ф (– x) = – Ф (x), для тех значений x, которых нет в таблице, т.е. для
, где Ф (– x) = – Ф (x), для тех значений x, которых нет в таблице, т.е. для  , Ф (x) =
, Ф (x) =  .
.
Теорема 2. (Теорема Муавра-Лапласа) Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < p < 1), событие А наступит не менее m 1раза и не более m 2раз приближенно равна:
 ,
,
где Ф (x) – функция Лапласа, значения  ,
,  .
.



 при
при  так, что
так, что  , где
, где  – среднее число появления события А в n испытаниях,
– среднее число появления события А в n испытаниях,  , то вероятность Pn (m) того, что в этих испытаниях событие А наступит ровно m раз, удовлетворяет при
, то вероятность Pn (m) того, что в этих испытаниях событие А наступит ровно m раз, удовлетворяет при 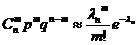 .
. , при этом
, при этом 
 .
. .
. . Найдем заданную вероятность:
. Найдем заданную вероятность: (перейдем к противоположному событию: m < 2) =
(перейдем к противоположному событию: m < 2) =  .
. , т.е. ошибка невелика.
, т.е. ошибка невелика. ,
, ,
,  .
. .
. .
. . Это означает, что n и m должны отличаться друг от друга не очень сильно. Например, для случая m = 0, теорема дает плохое приближение.
. Это означает, что n и m должны отличаться друг от друга не очень сильно. Например, для случая m = 0, теорема дает плохое приближение. , тогда
, тогда  .
. .
. ) при
) при  .
. или
или  .
. . Численное значение нашего интеграла можно найти с помощью таблиц (стр. 406 в задачнике Ефимова – Демидовича) для функции Лапласа Ф (x):
. Численное значение нашего интеграла можно найти с помощью таблиц (стр. 406 в задачнике Ефимова – Демидовича) для функции Лапласа Ф (x): , где Ф (– x) = 1 – Ф (x). Для тех значений x, которых нет в таблице, т.е для
, где Ф (– x) = 1 – Ф (x). Для тех значений x, которых нет в таблице, т.е для  , Ф (x) = 1.
, Ф (x) = 1. , где Ф (– x) = – Ф (x), для тех значений x, которых нет в таблице, т.е. для
, где Ф (– x) = – Ф (x), для тех значений x, которых нет в таблице, т.е. для  , Ф (x) =
, Ф (x) =  .
. ,
, ,
,  .
.


