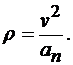Проведем в точке М кривой АВ соприкасающуюсяплоскость,нормальную плоскость, перпендикулярную касательной, и спрямляющуюплоскость, перпендикулярную соприкасающейся и нормальной плоскостям, образующую с этими плоскостями естественный трехгранник(рис. 9.1).

Рис. 9.1
Линия пересечения соприкасающейся и нормальной плоскостей называется главной нормалью кривой.
Линия пересечения нормальной и спрямляющей плоскостей называется бинормалью кривой.
Естественными координатными осями называются три взаимно перпендикулярные оси: касательная, направленная в сторону возрастания дуговой координаты, главная нормаль, направленная в сторону вогнутости кривой, и бинормаль, направленная по отношению к касательной и главной нормали так же, как ось Оz направлена по отношению к осям Ох и Оу в правой системе координатных осей. Единичные векторы-орты этих осей обозначаются соответственно  .
.
Естественные координатные оси имеют начало в точке М кривой и при движении точки М по этой кривой перемещаются вместе с ней, оставаясь взаимно перпендикулярными, но изменяя свое направление в пространстве.
Возьмем на кривой АВ две точки М и M 1, соответствующие дуговым координатам ОМ = s и ОМ =s+Δ s. Покажем орты касательной  и
и  в этих точках (рис. 9.2). Модуль орта
в этих точках (рис. 9.2). Модуль орта  , равный единице, постоянен, но направление орта изменяется при перемещении точки по кривой, т. е. орт
, равный единице, постоянен, но направление орта изменяется при перемещении точки по кривой, т. е. орт  является переменным вектором.
является переменным вектором.
Определим приращение орта  на участке mm 1=Δ s. Для этого отложим от точки М орт
на участке mm 1=Δ s. Для этого отложим от точки М орт  и построим при этой точке параллелограмм, одной из сторон которого будет орт
и построим при этой точке параллелограмм, одной из сторон которого будет орт  , а диагональю - орт
, а диагональю - орт  . Тогда другая сторона параллелограмма будет приращением орта
. Тогда другая сторона параллелограмма будет приращением орта  , так как
, так как  =
=  +Δ
+Δ  .
.
Разделим приращение орта  на приращение дуговой координаты Δs. Вектор
на приращение дуговой координаты Δs. Вектор  , характеризующий поворот касательной к кривой на участке MM 1, называется вектором средней кривизны кривой на участке ММ1. Этот вектор имеет направление вектора Δ
, характеризующий поворот касательной к кривой на участке MM 1, называется вектором средней кривизны кривой на участке ММ1. Этот вектор имеет направление вектора Δ  , т.е. направлен в сторону вогнутости кривой.
, т.е. направлен в сторону вогнутости кривой.


Рис. 9.2 Рис. 9.3
Предел  , к которому стремится вектор средней кривизны кривой
, к которому стремится вектор средней кривизны кривой  , когда Δs стремится к нулю, называется вектором кривизны кривой в данной точке:
, когда Δs стремится к нулю, называется вектором кривизны кривой в данной точке:
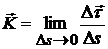 .
.
Орт касательной к кривой является вектор-функцией дуговой координаты s, так как его направление зависит от положения точки на кривой, т.е.  . Тогда
. Тогда
 .
.
Следовательно, вектор кривизны кривой в данной точке равен производной от орта касательной к кривой по дуговой координате.
Для определения модуля этого вектора рассмотрим равнобедренный треугольник, образованный  (рис. 9.2).
(рис. 9.2).
Угол ε между направлениями касательных в двух точках кривой М и M1 называется углом смежности. При малом расстоянии Δ s угол смежности тоже мал.
Модуль |Δτ| найдем как длину основания равнобедренного треугольника с малым углом ε при вершине и боковыми сторонами, равными единице. Тогда
 .
.
Модуль вектора кривизны К определяется по формуле
 .
.
Из дифференциальной геометрии известно, что предел отношения угла смежности ε к приращению дуговой координаты Δ s при стремлении Δ s к нулю равен кривизне кривой 1/ ρ, при ρ - радиус кривизны кривой в точке М. Таким образом, получим модуль вектора кривизны
 .
.
Установим также направление вектора кривизны. Вектор средней кривизны 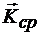 находится в плоскости треугольника, составленного векторами
находится в плоскости треугольника, составленного векторами  , предельным положением которого является соприкасающаяся плоскость. Следовательно, вектор кривизны
, предельным положением которого является соприкасающаяся плоскость. Следовательно, вектор кривизны  расположен в соприкасающейся плоскости.
расположен в соприкасающейся плоскости.
Рассмотрим угол β, составленный вектором 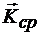 с касательной в точке М (рис. 9.2):
с касательной в точке М (рис. 9.2):
 .
.
При приближении точки М 1 к точке М угол смежности ε стремится к нулю, а поэтому
 .
.
Так кик вектор кривизны  расположен в соприкасающейся плоскости и перпендикулярен орту
расположен в соприкасающейся плоскости и перпендикулярен орту  , то он направлен по главной нормали к центру кривизны кривой (рис. 9.3).
, то он направлен по главной нормали к центру кривизны кривой (рис. 9.3).
Представим вектор  в виде произведения орта на модуль этого вектора:
в виде произведения орта на модуль этого вектора:
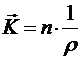 ,
,
где ρ = МС - радиус кривизны кривой в данной точке М.
Скорость и ускорение точки
Скорость точки
Определим скорость точки в случае, когда ее движение задано естественным способом, т. е. известныее траектория АВ, начало и направление отсчета дуговой координаты и уравнение движения точки  (рис. 9.4).
(рис. 9.4).


Рис. 9.4 Рис. 9.5
Пусть в момент времени t точка занимает положение М, а вмомент t 1= t +Δ t - положение М 1, Дуговые координаты этих точек имеют следующие значения:
 .
.
Приращение дуговой координаты  .
.
Проведем из произвольного центра О ’ в точку М радиус-вектор 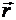 и определим скорость точки в момент t по формуле:
и определим скорость точки в момент t по формуле:
 .
.
Введем в качестве промежуточной переменной дуговую координату s, от которой зависит радиус-вектор 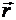 движущейся точки. Действительно, каждому значению s соответствует определенное значение
движущейся точки. Действительно, каждому значению s соответствует определенное значение 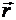 , т. е.
, т. е. 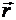 можно рассматривать не только как функцию t, но и как функцию s, полагая
можно рассматривать не только как функцию t, но и как функцию s, полагая  . Тогда
. Тогда
 .
.
Здесь
 .
.
Вектор  направлен так же, как вектор
направлен так же, как вектор  . При
. При  егонаправление стремится к направлению касательной, проведеннойизточки М в сторону увеличения дуговой координаты s. Модуль этого вектора стремится к единице:
егонаправление стремится к направлению касательной, проведеннойизточки М в сторону увеличения дуговой координаты s. Модуль этого вектора стремится к единице:
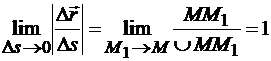 .
.
Таким образом, вектор  имеет модуль, равный единице, и направлен по касательной к кривой в сторону увеличения дуговой координаты. Вектор d
имеет модуль, равный единице, и направлен по касательной к кривой в сторону увеличения дуговой координаты. Вектор d 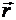 / ds является ортом этого направления. Обозначим этот орт
/ ds является ортом этого направления. Обозначим этот орт  (рис. 9.5):
(рис. 9.5):
 . (9.1)
. (9.1)
Пользуясь формулой (9.1), получаем вектор скорости в виде
 . (9.2)
. (9.2)
Производная ds/dt в выражении (9.2) представляет собой проекцию скорости 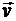 на касательную, т. е. определяет алгебраическую величину скорости.
на касательную, т. е. определяет алгебраическую величину скорости.
Условимся алгебраическую величину скорости обозначать символом 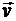 , а модуль скорости - v. Тогда
, а модуль скорости - v. Тогда
 , (9.3)
, (9.3)
а
 , (9.4)
, (9.4)
т. е. модуль скорости равен абсолютному значению производной от дуговой координаты точки по времени.
Орт касательной  , как показано выше, всегда направлен в сторону увеличения дуговой координаты.
, как показано выше, всегда направлен в сторону увеличения дуговой координаты.
Если в некоторый момент времени ds/dt > 0, то в этот момент функция s возрастает, т.е. точка движется в сторону увеличения s и направление скорости 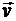 совпадает с направлением орта
совпадает с направлением орта  (рис. 9.6, а). Если ds/dt < 0, то в этот момент функция s убывает в направление скорости
(рис. 9.6, а). Если ds/dt < 0, то в этот момент функция s убывает в направление скорости 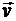 противоположно направлению орта
противоположно направлению орта  (рис. 9.6, б).
(рис. 9.6, б).

Рис. 9.6
Если, непрерывно изменяясь, производная ds/dt при переходе через значение ds/dt= 0 изменяет знак, то дуговая координата s в этот момент времени достигает максимумаилиминимума, т. е. изменяется направление движения точки.
Таким образом, знак 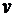 = ds/dt указывает направление движения точки по траектории. При движении точки в сторону возрастания дуговой координаты ds/dt > 0, т. е.
= ds/dt указывает направление движения точки по траектории. При движении точки в сторону возрастания дуговой координаты ds/dt > 0, т. е.  во все моменты времени, а потому модуль скорости
во все моменты времени, а потому модуль скорости
 .(9.5)
.(9.5)
Ускорение точки
Определим проекции ускорения точки на естественные координатные оси. Для этого представим вектор скорости точки по формуле:
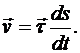
Определим ускорение точки, продифференцировав по t произведение двух переменных величии:

Найдем

Так как проекция скорости на касательную  может отличаться от модуля скорости v только знаком, то
может отличаться от модуля скорости v только знаком, то

Подставив эти выражения, получим вектор ускорения в виде
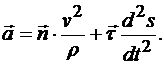 (9.6)
(9.6)
Ускорение точки равно геометрической сумме двух векторов, один из которых направлен по главной нормали и называется нормальным ускорением, а другой направлен по касательной и называется касательным ускорением точки (рис. 9.8):
 (9.7)
(9.7)
где нормальное ускорение точки
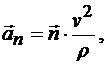 (9.8)
(9.8)
а касательное ускорение точки
 (9.9)
(9.9)
Скалярные множители  и
и  в выражениях (9.8) и 9.(9), определяющих нормальное и касательное ускорения точки, представляют собой проекции ускорения точки на главную нормаль и касательную.
в выражениях (9.8) и 9.(9), определяющих нормальное и касательное ускорения точки, представляют собой проекции ускорения точки на главную нормаль и касательную.
Проекция ускорения точки на бинормаль оказалась равной нулю, так как вектор ускорения расположен в соприкасающейся плоскости (рис. 9.7).
Согласно формуле (8),
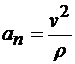 , (9.10)
, (9.10)

Рис. 9.7
т. е. проекция ускорения точки на главную нормаль равна квадрату модуля скорости точки, деленному на радиус кривизны траектории в соответствующей точке. Эта проекция всегда положительна. Из этого следует, что нормальное ускорение точки всегда направлено к центру кривизны траектории и равно по модулю этой проекции.
Условимся алгебраическую величину касательного ускорения обозначать  , а его модуль
, а его модуль  . Согласно формуле (9.9)
. Согласно формуле (9.9)
 (9.11)
(9.11)
т.е. проекция ускорения точки на касательную равна второй производной от дуговой координаты точки по времени или первой производной от алгебраической величины скорости точки по времени.
Эта проекция имеет знак плюс, если направления касательного ускорения точки  и орта
и орта  совпадают, и знак минус, если они противоположны. Очевидно, что
совпадают, и знак минус, если они противоположны. Очевидно, что
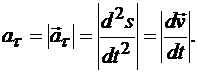 (9.12)
(9.12)
Таким образом, в случае естественного способа задания движения, когда известны траектория точки, а следовательно, ее радиус кривизны ρ в любой точке и уравнение движения s=f(t), можно найти проекции ускорения точки на естественные оси и по ним определить модуль и направление ускорения точки:
 ,
,
где  и
и  - углы, образованные направлением ускорения с принятыми направлениями касательной и главной нормали в данной точке.
- углы, образованные направлением ускорения с принятыми направлениями касательной и главной нормали в данной точке.
Если проекции скорости 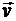 и касательного ускорения
и касательного ускорения  , на касательную
, на касательную  и
и  , имеют одинаковые знаки, то и направления этих векторов совпадают, т. е. точка движется ускоренно.
, имеют одинаковые знаки, то и направления этих векторов совпадают, т. е. точка движется ускоренно.
Если же их проекции  и
и 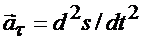 имеют различные знаки, то и направления
имеют различные знаки, то и направления  и
и  , противоположны, т.е. точка движется замедленно.
, противоположны, т.е. точка движется замедленно.
Модуль касательного ускорения точки  , можно также определить по формуле
, можно также определить по формуле
 (9.13)
(9.13)
где v - модуль скорости точки.
При этом, если dv/dt > 0, т. е. модуль скорости возрастает, точка движется ускоренно, а если dv/dt < 0 — замедленно.
При прямолинейном движении точки радиус кривизны траектории  и, следовательно,
и, следовательно,
 .
.
Нормальное ускорение существует лишь при криволинейном движении точки и характеризует изменение направления скорости.
При равномерном движении точки v=const и, следовательно,

Касательное ускорение точки существует лишь при неравномерном движении точки и характеризует изменение модуля скорости.
В том случае, если требуется определить касательное и нормальное ускорения движения точки, заданного уравнениями движения, то сначала по формулам определяют модули скорости и ускорения точки:

Согласно формуле (9.13)

или

где знак плюс, полученный в ответе после вычисления дроби соответствует ускоренному движению точки, а знак минус - замедленному. Нормальное ускорение точки определяется по формуле:

Радиус кривизны кривой находим по формуле (9.10):
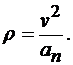




 .
. и
и  в этих точках (рис. 9.2). Модуль орта
в этих точках (рис. 9.2). Модуль орта  , так как
, так как  =
=  .
. , характеризующий поворот касательной к кривой на участке MM 1, называется вектором средней кривизны кривой на участке ММ1. Этот вектор имеет направление вектора Δ
, характеризующий поворот касательной к кривой на участке MM 1, называется вектором средней кривизны кривой на участке ММ1. Этот вектор имеет направление вектора Δ 

 , к которому стремится вектор средней кривизны кривой
, к которому стремится вектор средней кривизны кривой  , когда Δs стремится к нулю, называется вектором кривизны кривой в данной точке:
, когда Δs стремится к нулю, называется вектором кривизны кривой в данной точке: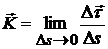 .
. . Тогда
. Тогда .
. (рис. 9.2).
(рис. 9.2). .
. .
. .
.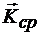 находится в плоскости треугольника, составленного векторами
находится в плоскости треугольника, составленного векторами  , предельным положением которого является соприкасающаяся плоскость. Следовательно, вектор кривизны
, предельным положением которого является соприкасающаяся плоскость. Следовательно, вектор кривизны  расположен в соприкасающейся плоскости.
расположен в соприкасающейся плоскости. .
. .
. ,
, (рис. 9.4).
(рис. 9.4).

 .
. .
.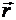 и определим скорость точки в момент t по формуле:
и определим скорость точки в момент t по формуле: .
. . Тогда
. Тогда .
. .
. направлен так же, как вектор
направлен так же, как вектор  . При
. При  егонаправление стремится к направлению касательной, проведеннойизточки М в сторону увеличения дуговой координаты s. Модуль этого вектора стремится к единице:
егонаправление стремится к направлению касательной, проведеннойизточки М в сторону увеличения дуговой координаты s. Модуль этого вектора стремится к единице: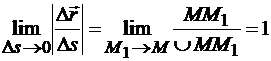 .
. имеет модуль, равный единице, и направлен по касательной к кривой в сторону увеличения дуговой координаты. Вектор d
имеет модуль, равный единице, и направлен по касательной к кривой в сторону увеличения дуговой координаты. Вектор d  . (9.1)
. (9.1) . (9.2)
. (9.2) на касательную, т. е. определяет алгебраическую величину скорости.
на касательную, т. е. определяет алгебраическую величину скорости. , (9.3)
, (9.3) , (9.4)
, (9.4)
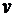 = ds/dt указывает направление движения точки по траектории. При движении точки в сторону возрастания дуговой координаты ds/dt > 0, т. е.
= ds/dt указывает направление движения точки по траектории. При движении точки в сторону возрастания дуговой координаты ds/dt > 0, т. е.  во все моменты времени, а потому модуль скорости
во все моменты времени, а потому модуль скорости .(9.5)
.(9.5)


 может отличаться от модуля скорости v только знаком, то
может отличаться от модуля скорости v только знаком, то
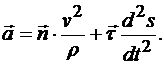 (9.6)
(9.6) (9.7)
(9.7)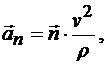 (9.8)
(9.8) (9.9)
(9.9) и
и  в выражениях (9.8) и 9.(9), определяющих нормальное и касательное ускорения точки, представляют собой проекции ускорения точки на главную нормаль и касательную.
в выражениях (9.8) и 9.(9), определяющих нормальное и касательное ускорения точки, представляют собой проекции ускорения точки на главную нормаль и касательную.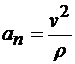 , (9.10)
, (9.10)
 , а его модуль
, а его модуль  . Согласно формуле (9.9)
. Согласно формуле (9.9) (9.11)
(9.11) и орта
и орта 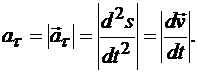 (9.12)
(9.12) ,
, и
и  - углы, образованные направлением ускорения с принятыми направлениями касательной и главной нормали в данной точке.
- углы, образованные направлением ускорения с принятыми направлениями касательной и главной нормали в данной точке. и
и  , имеют одинаковые знаки, то и направления этих векторов совпадают, т. е. точка движется ускоренно.
, имеют одинаковые знаки, то и направления этих векторов совпадают, т. е. точка движется ускоренно. и
и 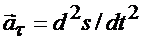 имеют различные знаки, то и направления
имеют различные знаки, то и направления  и
и  , противоположны, т.е. точка движется замедленно.
, противоположны, т.е. точка движется замедленно. (9.13)
(9.13) и, следовательно,
и, следовательно, .
.