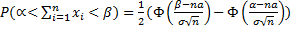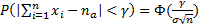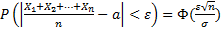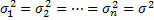Функция  называется функцией Лапласа или интегралом вероятности. Она тесно связана с нормальным законом распределения. Ее основные свойства:
называется функцией Лапласа или интегралом вероятности. Она тесно связана с нормальным законом распределения. Ее основные свойства:
1) область определения функции Лапласа – вся числовая ось;
2) функция Лапласа монотонно возрастает на всей числовой прямой, т.к.  ;
;
3) функция  - нечетная, покажем это.
- нечетная, покажем это.

4)  . Действительно,
. Действительно, 
График.
Итак, пусть у нас имеется нормальная случайная величина X с математическим ожиданием а и дисперсией  . Тогда функция распределения этой случайной величины
. Тогда функция распределения этой случайной величины
 .
.
Сделаем замену переменной в этом интеграле, положив  . Тогда
. Тогда  , при
, при  ,
,  , при
, при  ,
,  .
.
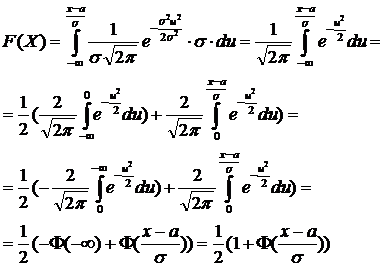
Если  , то случайная величина называется нормированной. График функции распределения нормированной нормальной случайной величины с математическим ожиданием
, то случайная величина называется нормированной. График функции распределения нормированной нормальной случайной величины с математическим ожиданием  , т.е.
, т.е.  имеет вид:
имеет вид:
Найдем вероятность того, что случайная величина 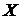 , распределенная по нормальному закону с параметрами
, распределенная по нормальному закону с параметрами  ,
,  , примет значение из
, примет значение из 

Таким образом,
 .
.
Найдем вероятность того, что отклонение нормальной случайной величины от ее математического ожидания по модулю меньше некоторого положительного  , т.е. найдем вероятность
, т.е. найдем вероятность
 .
.

Итак:  .
.
Вероятность того, что нормальная случайная величина отклоняется от своего математического ожидания по модулю меньше, чем на  , определяется формулой
, определяется формулой
 .
.
Если в этой формуле положить  , то получим
, то получим
 .
.
Отсюда вытекает, что среди 10000 значений нормальной случайной величины в среднем только 27 выйдут за пределы интервала  . Это означает, что практически среди небольшого числа значений
. Это означает, что практически среди небольшого числа значений 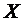 нет таких, которые выходят за пределы указанного интервала. В этом и состоит правило «трех сигм», которое широко применяется в статистике.
нет таких, которые выходят за пределы указанного интервала. В этом и состоит правило «трех сигм», которое широко применяется в статистике.
Неравенство Маркова
Теорема. Если случайная величина 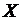 может принимать только неотрицательные значения и у нее есть математическое ожидание, то какова бы ни была величина
может принимать только неотрицательные значения и у нее есть математическое ожидание, то какова бы ни была величина 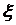 той же размерности, что и
той же размерности, что и 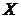 , всегда выполняется неравенство
, всегда выполняется неравенство
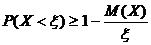 .
.
Доказательство. Пусть 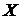 - непрерывная случайная величина с плотностью распределения
- непрерывная случайная величина с плотностью распределения 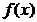 . Из условия теоремы следует, что
. Из условия теоремы следует, что 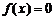 при
при 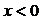 и
и 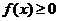 при
при 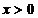 .
.
Математическое ожидание случайной величины 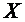 -
-
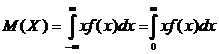 (разобьем на два интеграла)
(разобьем на два интеграла)
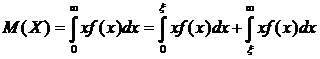 .
.
Так как 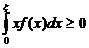 , то
, то 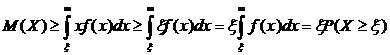 .
.
Итак,
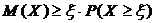 ,
, 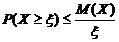 .
.
Если это неравенство вычесть из тождества 1=1, то
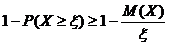 или
или 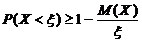 . Что и требовалось доказать.
. Что и требовалось доказать.
Пример. Средний срок службы мотора 4 года. Оценить снизу вероятность того, что данный мотор не прослужит 20 лет.
Решение. Пусть случайная величина 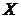 - срок службы мотора. Из условия задачи -
- срок службы мотора. Из условия задачи - 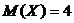 . Требуется оценить снизу вероятность
. Требуется оценить снизу вероятность 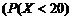 . Эту вероятность можно рассматривать как левую часть неравенства Маркова с
. Эту вероятность можно рассматривать как левую часть неравенства Маркова с 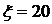 . Тогда
. Тогда
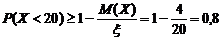 .
.
Пример. Сумма всех вкладов в некотором сберегательном банке составляет 2 млн. рублей, вероятность того, что случайно взятый вклад не превышает 10000 руб. равна 0.8. Что можно сказать о числе вкладчиков данного сберегательного банка?
Решение. Пусть 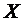 - величина случайно взятого вклада, а
- величина случайно взятого вклада, а 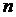 - число всех вкладчиков. Тогда из условия задачи следует, что
- число всех вкладчиков. Тогда из условия задачи следует, что 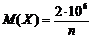 . Так как
. Так как 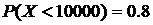 , то по неравенству Маркова получим
, то по неравенству Маркова получим 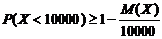 или
или
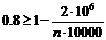 ,
, 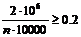 ,
, 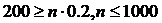 .
.
Неравенство Чебышева
Теорема. Каково бы ни было 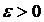 для любой случайной величины
для любой случайной величины 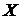 , дисперсия которой конечна, имеет место неравенство Чебышева
, дисперсия которой конечна, имеет место неравенство Чебышева
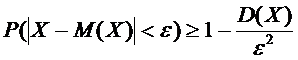 .
.
Доказательство. Рассмотрим величину 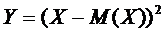 .
.
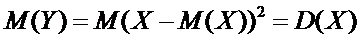 .
.
Для 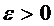 получим
получим
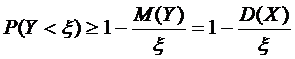 .
.
Подставим в это неравенство выражение 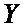 через
через 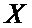 и
и 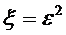
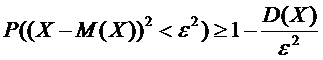 или
или
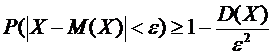
Примеры.
Определение. Последовательность чисел 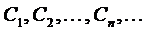 называется равномерно ограниченной, если существует такая постоянная М, что для любого
называется равномерно ограниченной, если существует такая постоянная М, что для любого 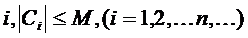 .
.
Теорема Чебышева
Если 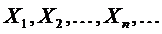 - последовательность попарно независимых случайных величин, у каждой из которых есть математическое ожидание
- последовательность попарно независимых случайных величин, у каждой из которых есть математическое ожидание 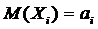 и дисперсия
и дисперсия 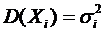 ,
, 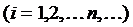 , причем дисперсии равномерно ограничены, то для любого положительного
, причем дисперсии равномерно ограничены, то для любого положительного 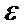
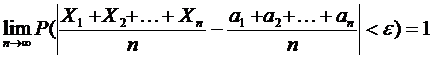
Доказательство.
Последовательность 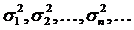 равномерно ограничена, т.е. существует такое М, что для любого натурального
равномерно ограничена, т.е. существует такое М, что для любого натурального 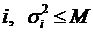 . Рассмотрим случайную величину
. Рассмотрим случайную величину
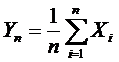 . У этой величины есть математическое ожидание и дисперсия:
. У этой величины есть математическое ожидание и дисперсия:
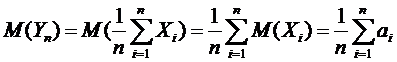 ,
,
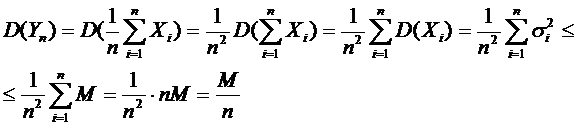
Здесь мы воспользовались свойством, что если случайные величины независимы, то дисперсия их суммы равна сумме их дисперсий.
Таким образом, 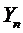 удовлетворяет всем требованиям для применения неравенства Чебышева, а значит, при любом
удовлетворяет всем требованиям для применения неравенства Чебышева, а значит, при любом 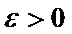 имеем
имеем
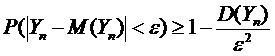 или
или
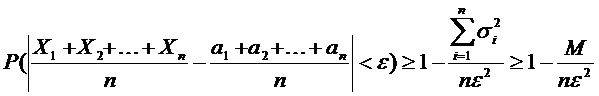
Итак,
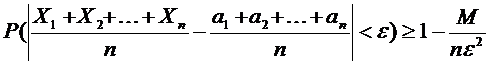
Пусть 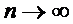 , тогда
, тогда 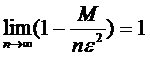 при любых
при любых 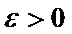 .
.
Отсюда 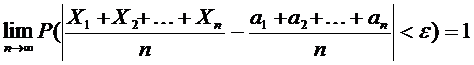 , что и требовалось доказать.
, что и требовалось доказать.
Следствие.
Если 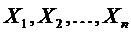 - последовательность независимых случайных величин, математические ожидания каждой из которых равны
- последовательность независимых случайных величин, математические ожидания каждой из которых равны 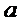 , а дисперсии
, а дисперсии 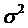 , то ……………
, то ……………
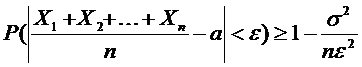
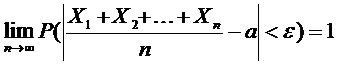
( )
) 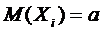
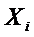
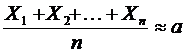
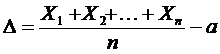
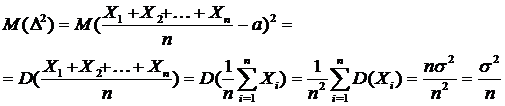
Отсюда следует 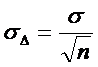 ,
,
Если точность всех измерений одна и та же, т.е. 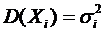 , i=1,2,…
, i=1,2,…
Теорема Бернулли
S n A p
Пусть случайная величина 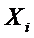 - число наступлений события А в i -ом испытании.
- число наступлений события А в i -ом испытании.
Следовательно,
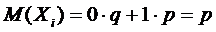
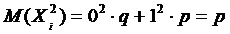
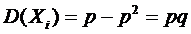
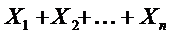 через m, то
через m, то
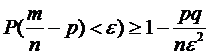 или
или 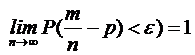
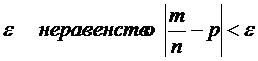
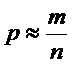
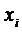
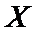
| i
|
|
|
|
|
| …
|
|
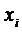
|
|
|
|
|
| …
|
|
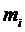
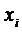 ,
, 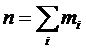
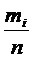
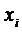
Теорема Ляпунова
Можно доказать, что CBX1X2…Xn –являются независим нормально распределенными CB, то сумма также распределена по номмальному закону с мат. Ожиданием равным сумме мат. ожиданий и дисперсией равной сумме дисперсий. Обобщением этого утверждения является следующая Т. Ляпунова
Т. Если X1X2…Xn –независимые CB, у каждой из которых существует мат ожидание и диспепсия 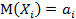 ,
, 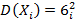 ,
, 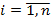 также существует
также существует 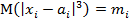 , а также
, а также
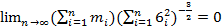 , тогда сумма S=X1+X2+…+Xn распределена асимптотически по нормальному закону с мат ожид равным сумме мат ожид и дисперсий равной сумме дисперсий, тогда для
, тогда сумма S=X1+X2+…+Xn распределена асимптотически по нормальному закону с мат ожид равным сумме мат ожид и дисперсий равной сумме дисперсий, тогда для 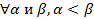
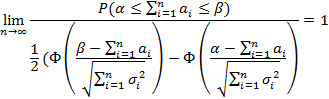
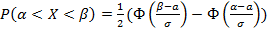 – ранее вывели. Ф-ция Лапласа.
– ранее вывели. Ф-ция Лапласа.
Следствием из Т. Липунова являются следующие неравенства:
1) 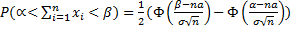
2) 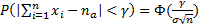
3) 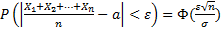
Здесь γ и ε –любые положительные числа, а также a1=a2=…=an=a, 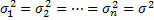
Например, если производятся измерения некоторой величины, истинное значение которой равно a, то среднее арифметическое значение результатов измерений отличается от истинного значения по модулю меньше чем ε с вероятностью прибл равной 



 называется функцией Лапласа или интегралом вероятности. Она тесно связана с нормальным законом распределения. Ее основные свойства:
называется функцией Лапласа или интегралом вероятности. Она тесно связана с нормальным законом распределения. Ее основные свойства: ;
; - нечетная, покажем это.
- нечетная, покажем это.
 . Действительно,
. Действительно, 
 . Тогда функция распределения этой случайной величины
. Тогда функция распределения этой случайной величины .
. . Тогда
. Тогда  , при
, при  ,
,  , при
, при  ,
,  .
.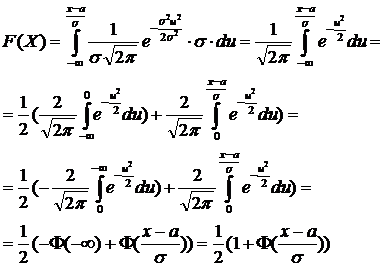
 , то случайная величина называется нормированной. График функции распределения нормированной нормальной случайной величины с математическим ожиданием
, то случайная величина называется нормированной. График функции распределения нормированной нормальной случайной величины с математическим ожиданием  , т.е.
, т.е.  имеет вид:
имеет вид: , распределенная по нормальному закону с параметрами
, распределенная по нормальному закону с параметрами  ,
,  , примет значение из
, примет значение из 

 .
. , т.е. найдем вероятность
, т.е. найдем вероятность .
.
 .
. , определяется формулой
, определяется формулой .
. , то получим
, то получим .
. . Это означает, что практически среди небольшого числа значений
. Это означает, что практически среди небольшого числа значений  нет таких, которые выходят за пределы указанного интервала. В этом и состоит правило «трех сигм», которое широко применяется в статистике.
нет таких, которые выходят за пределы указанного интервала. В этом и состоит правило «трех сигм», которое широко применяется в статистике.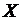 может принимать только неотрицательные значения и у нее есть математическое ожидание, то какова бы ни была величина
может принимать только неотрицательные значения и у нее есть математическое ожидание, то какова бы ни была величина 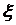 той же размерности, что и
той же размерности, что и 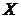 , всегда выполняется неравенство
, всегда выполняется неравенство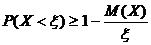 .
.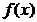 . Из условия теоремы следует, что
. Из условия теоремы следует, что 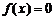 при
при 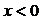 и
и 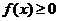 при
при 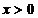 .
.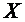 -
-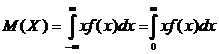 (разобьем на два интеграла)
(разобьем на два интеграла)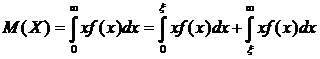 .
.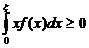 , то
, то 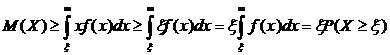 .
.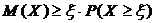 ,
, 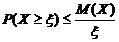 .
.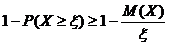 или
или 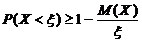 . Что и требовалось доказать.
. Что и требовалось доказать.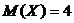 . Требуется оценить снизу вероятность
. Требуется оценить снизу вероятность 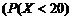 . Эту вероятность можно рассматривать как левую часть неравенства Маркова с
. Эту вероятность можно рассматривать как левую часть неравенства Маркова с 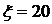 . Тогда
. Тогда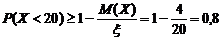 .
.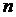 - число всех вкладчиков. Тогда из условия задачи следует, что
- число всех вкладчиков. Тогда из условия задачи следует, что 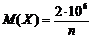 . Так как
. Так как 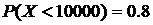 , то по неравенству Маркова получим
, то по неравенству Маркова получим 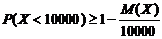 или
или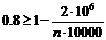 ,
, 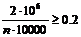 ,
, 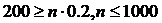 .
.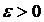 для любой случайной величины
для любой случайной величины 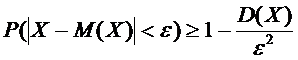 .
.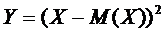 .
.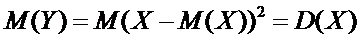 .
.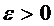 получим
получим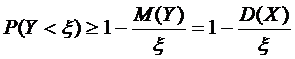 .
.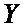 через
через 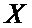 и
и 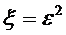
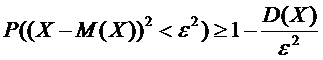 или
или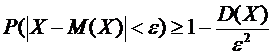
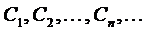 называется равномерно ограниченной, если существует такая постоянная М, что для любого
называется равномерно ограниченной, если существует такая постоянная М, что для любого 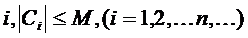 .
.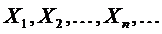 - последовательность попарно независимых случайных величин, у каждой из которых есть математическое ожидание
- последовательность попарно независимых случайных величин, у каждой из которых есть математическое ожидание 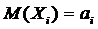 и дисперсия
и дисперсия 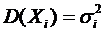 ,
, 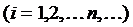 , причем дисперсии равномерно ограничены, то для любого положительного
, причем дисперсии равномерно ограничены, то для любого положительного 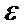
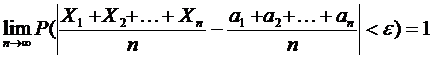
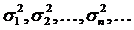 равномерно ограничена, т.е. существует такое М, что для любого натурального
равномерно ограничена, т.е. существует такое М, что для любого натурального 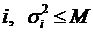 . Рассмотрим случайную величину
. Рассмотрим случайную величину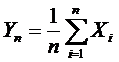 . У этой величины есть математическое ожидание и дисперсия:
. У этой величины есть математическое ожидание и дисперсия: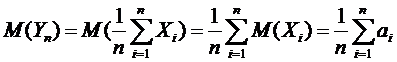 ,
,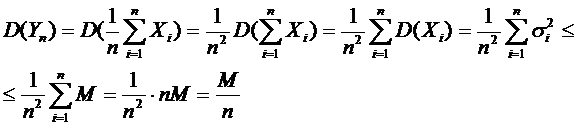
 удовлетворяет всем требованиям для применения неравенства Чебышева, а значит, при любом
удовлетворяет всем требованиям для применения неравенства Чебышева, а значит, при любом 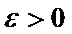 имеем
имеем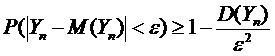 или
или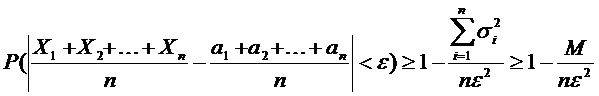
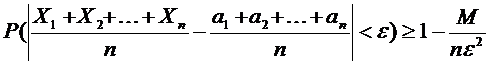
 , тогда
, тогда 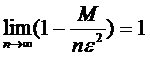 при любых
при любых 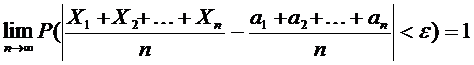 , что и требовалось доказать.
, что и требовалось доказать.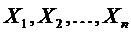 - последовательность независимых случайных величин, математические ожидания каждой из которых равны
- последовательность независимых случайных величин, математические ожидания каждой из которых равны 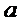 , а дисперсии
, а дисперсии 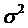 , то ……………
, то ……………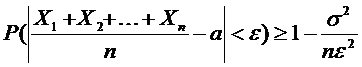
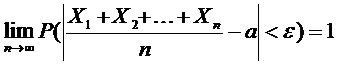
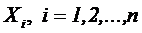 )
) 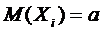
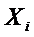
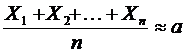
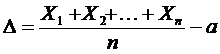
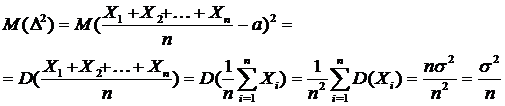
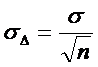 ,
,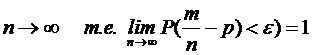
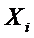 - число наступлений события А в i -ом испытании.
- число наступлений события А в i -ом испытании.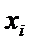
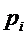
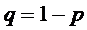
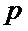
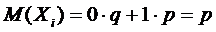
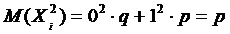
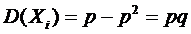
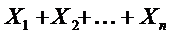 через m, то
через m, то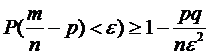 или
или 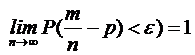
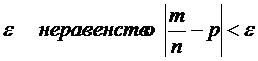
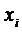
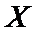
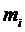
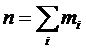
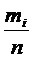
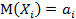 ,
, 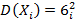 ,
, 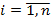 также существует
также существует 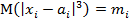 , а также
, а также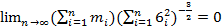 , тогда сумма S=X1+X2+…+Xn распределена асимптотически по нормальному закону с мат ожид равным сумме мат ожид и дисперсий равной сумме дисперсий, тогда для
, тогда сумма S=X1+X2+…+Xn распределена асимптотически по нормальному закону с мат ожид равным сумме мат ожид и дисперсий равной сумме дисперсий, тогда для 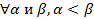
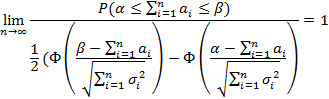
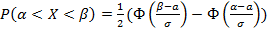 – ранее вывели. Ф-ция Лапласа.
– ранее вывели. Ф-ция Лапласа.