

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров...
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Интересное:
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Теорема. Пусть функция двух переменных  и ее частные производ-ные
и ее частные производ-ные  и
и  непрерывны в некоторой окрестности точки
непрерывны в некоторой окрестности точки  , причем:
, причем:  а
а  Тогда уравнение
Тогда уравнение  определяет (в не-которой окрестности точки
определяет (в не-которой окрестности точки  ) единственную функцию
) единственную функцию  . Эта функция дифференцируема и
. Эта функция дифференцируема и
 (1)
(1)
Докажем формулу (1), принимая без доказательства существование и дифференцируемость неявной функции  . То, что уравнение
. То, что уравнение  определяет некоторую функцию
определяет некоторую функцию  , означает следующее:
, означает следующее:  (в не-которой окрестности точки
(в не-которой окрестности точки  ). Продифференцируем это тождество почленно, используя формулу (2) предыдущего параграфа:
). Продифференцируем это тождество почленно, используя формулу (2) предыдущего параграфа:


Из последнего равенства и вытекает формула (1).
Пример. Рассмотрим функцию  и точку
и точку  Вычислим производные:
Вычислим производные:  Нетрудно видеть, что все условия теоремы выполнены:
Нетрудно видеть, что все условия теоремы выполнены:  непрерывны в окрестности точки
непрерывны в окрестности точки  и
и  ,
,  Следовательно, в некоторой окрестности точки
Следовательно, в некоторой окрестности точки  , уравнение
, уравнение  определяет некоторую функцию
определяет некоторую функцию  , обращающую уравнение в тождество. Ее производная:
, обращающую уравнение в тождество. Ее производная:

Замечательно, что по свойствам функции двух переменных  , задан-ной непосредственно, мы можем судить о свойствах функции
, задан-ной непосредственно, мы можем судить о свойствах функции  , для которой непосредственного задания мы не имеем.
, для которой непосредственного задания мы не имеем.
Замечание 1. Геометрический смысл условия  линия определяемая уравнением
линия определяемая уравнением  имеет в точке
имеет в точке  невертикальную касательную, т.е. саму линию можно понимать как график некоторой функции (в некоторой окрестности точки М 0).
невертикальную касательную, т.е. саму линию можно понимать как график некоторой функции (в некоторой окрестности точки М 0).
Замечание 2. Теорема легко обобщается на случай неявных функций нескольких переменных.
Лекция 19
Касательная к кривой в пространстве
I Вектор-функция и ее производная
Определение 1. Если каждому значению переменной t из некоторого мно-жества Т поставлен в соответствие некоторый вектор 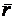 , то говорят, что на множестве Т задана вектор-функция
, то говорят, что на множестве Т задана вектор-функция 
Определение 2. Вектор  называют пределом вектор-функции
называют пределом вектор-функции  в точке
в точке  и пишут
и пишут  , если
, если  .
.
|
|
Определение 3. Производной вектор-функции  в точке
в точке  называют предел
называют предел

Если в пространстве задана декартова прямоугольная система координат, то вектор определяется своими проекциями, т.е.
 или
или  .
.
Таким образом, вектор-функция – это упорядоченная тройка обычных функций одной переменной. А так как
 ,
,
то определение 2 равносильно следующим трем равенствам
 .
.
Аналогично для производной получаем
 .
.
Будем откладывать векторы  ,
,  , от начала координат. Тогда их концы составят в пространстве некоторую линию, которую называют годографом вектор-функции
, от начала координат. Тогда их концы составят в пространстве некоторую линию, которую называют годографом вектор-функции  . Например, для вектор-функции
. Например, для вектор-функции  годограф – это винтовая линия.
годограф – это винтовая линия.
II Физический смысл производной вектор-функции
Положение точки М в пространстве можно задавать ее координатами (в не-которой системе координат), а можно задавать и радиус-вектором  , где О – начало координат. Если точка М движется, то
, где О – начало координат. Если точка М движется, то 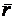 зависит от времени, т.е. движение точки в пространстве можно задавать вектор-функцией
зависит от времени, т.е. движение точки в пространстве можно задавать вектор-функцией  , где t – время из некоторого промежутка. Годограф этой функции – это траектория дви-жения. Производная
, где t – время из некоторого промежутка. Годограф этой функции – это траектория дви-жения. Производная 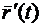 – это вектор мгновенной скорости:
– это вектор мгновенной скорости:
 .
.
III Уравнения касательной
Линию в пространстве обычно задают системой параметрических урав-нений

Однако, удобно такую линию понимать как годограф вектор-функции
 .
.
Напомним, что, кратко говоря, касательная к линии L в ее точке  –это пре-дельной положение секущей
–это пре-дельной положение секущей  , когда точка
, когда точка 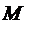 стремиться к
стремиться к  вдоль L. Другими словами, касательная в точке
вдоль L. Другими словами, касательная в точке  – это та прямая, проходящая через
– это та прямая, проходящая через  , направляющий вектор которой есть предел направляющего вектора секущей. Пусть
, направляющий вектор которой есть предел направляющего вектора секущей. Пусть  и
и  Тогда
Тогда
 ,
,
т.е. 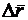 , а следовательно и
, а следовательно и  служат направляющими векторами секущей. Поэтому
служат направляющими векторами секущей. Поэтому

Отсюда получаем два вывода:
1)вектор мгновенной скорости точки направлен по касательной к траек-тории движения;
2)канонические уравнения касательной к линии L в точке  , которая соответствует значению параметра
, которая соответствует значению параметра  , имеют вид:
, имеют вид:

|
|
Пример. Показать, что касательные к линии  образуют с осью
образуют с осью  постоянный угол.
постоянный угол.
Решение. Для винтовой линии направляющий вектор касательной 
 . Если
. Если  – угол между касательной и осью
– угол между касательной и осью  , то
, то
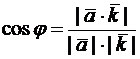 .
.
Напомним, что  – орт оси
– орт оси  :
:  . Значит,
. Значит,
 .
.
Как видим,  , а значит и
, а значит и  , не зависят от параметра t, т.е
, не зависят от параметра t, т.е  = сonst.
= сonst.
Замечание. Нетрудно заметить, что для плоской линии
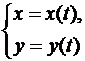
уравнение касательной имеет вид
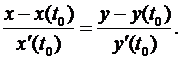
Пример. Составить уравнение касательной к эллипсу 
Решение. Пусть  – точка касания, соответствующая значению параметра
– точка касания, соответствующая значению параметра  :
:  . Тогда уравнение касательной:
. Тогда уравнение касательной:

Разделив обе части последнего равенства на а . b, получим известную формулу для касательной к эллипсу в его точке  :
:
 .
.
|
|
|

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!