Свойства операций над множествами

Введение

Если к разным частям слона подвести трёх священников с повязками на глазах, то потом, обменявшись мнениями о том, что они чувствовали, они придут к мнению, что они имеют дело с непостижимым созданием Бога, ибо неисповедимы пути Его.

Если к слону подвести трёх физиков с повязками на глазах, то они придут к мнению, что слон – это некий объект, в разных экспериментах проявляющий себя по – разному: например, как давилка, как каталка или даже как поливалка. Они назовут это дуализмом, изначально присущем природе, и поскольку полностью индивидуализированных объектов в природе не существует, надо рассматривать класс таких объектов, выяснить границы слоноподобности, построить их теоретические модели и утешатся мыслью о будущей единой теории.

Математики, даже без повязок, к слону не пойдут. Они выслушают священников и физиков и начнут создавать общую и непротиворечивую теорию того, что услышали, исходя из конечного числа конструктивных принципов. При этом окажется, что, с одной стороны, слон здесь совсем даже не важен, это просто один из возможных элементов носителей пространств. С другой стороны слон должен быть включён в определённого рода слоноподобные структуры, в которых слон тоже никакой роли не играет. Это и приводит нас к высшей алгебре и функциональному анализу.

Сторожа зоопарка Митрича, ухаживавшего за слоном и на исконно русском языке пытавшегося им объяснить, что же такое слон, все они на том же самом языке прогоняли прочь…

“Но, господа, забавный случай сей” на мысль одну престранную наводит. Кого, кроме маленьких детей и умственно отсталых интересует конкретный слон? Нам интересен не факт существования конкретного объекта, а система, в которой он существует, причины и условия её появления и проявления.

Священники считают, что это Бог, который, по крайней мере, в христианстве есть в нас и Он есть Любовь, позволяющая постигнуть Истину, Добро и Красоту. Им не интересна природа, им интересна первопричина и её проявления в нас.

Физикам Природа интересна, им также интересны первопричины появления Мира, то есть что произошло “при родах” Вселенной, по каким законам она развивается. Они полагают, что всё подчиняется вполне определённым законам, и мы их поймём, не обращаясь к другим Вселенным, которых просто нет. Но глаза физики 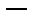это математика. Поэтому важно понять, как устроен этот инструмент, чтобы знать, где мы видим “ то, что есть”, а где миражи и иллюзии.

Математики же ищут общие конструктивные принципы, позволяющие с единых позиций понять, как устроена математика, благодаря которой мы и смотрим на Вселенную, если наши мозги работают логично. Та “реальность”, которую изучают математики, включает в себя все возможные с математической и логической точки зрения Вселенные. Во многом прав Г.В. Лейбниц, который назвал математику физикой возможных Миров.

Одна из главных конструктивных идей, позволяющих обосновать математику, это идея сходимости, которая опирается на идею бесконечности. Собственно говоря, функциональный анализ это песнь о сходимости. Всё остальное реквизит (requisitum (лат.) необходимое) для её исполнения.

 

 

ЛИТЕРАТУРА

1. Бронштейн Е.М. Основы функционального анализа. Уфа: УГАТУ, 2004.- 62 с.

2. Канторович Л.В., Акилов Г.П. Функциональный анализ. Наука, 1984.

3. Князев П.Н. Функциональный анализ. Минск, «Вышэйшая школа»,1985.

4. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. Наука, 2002.

5. Люстерник Л.А., Соболев В.И. Краткий курс функционального анализа. Высшая школа, 1982.

6. Ольховой А.Ф. Введение в функциональный анализ. Таганрог, 2011.-146с.

7. Пугачев В.С. Лекции по функциональному анализу. М., Изд. МАИ. 1996.

8. Садовничий В.А. Теория операторов. М., Высшая школа, 1999.

9. Треногин В.А. и др. Задачи и упражнения по функциональному анализу. М., Мир, 1984.

10. Треногин В.А. Функциональный анализ. Высшая школа, 2002.

11. Функциональный анализ. Под редакцией С.Г. Крейна. М., Наука, 1964.

I. НОСИТЕЛИ ПРОСТРАНСТВ

 

Никто не сможет изгнать нас из рая, который

создал для нас Георг Кантор!

Д.Гильберт

Теория Кантора в целом является патологическим казусом

в истории математики, от которого грядущие поколения придут в ужас.

Л.Брауэр

 

 

1. ГЛАВНЫЕ ПЕСНИ О СТАРОМ

Всё не так просто, как кажется. И даже просто не так.

Алекс Алдер

Определение 1. Множество – совокупность элементов, связанных между собой определёнными отношениями, а с элементами других множеств определёнными соответствиями.

Замечание. “Множество есть многое, мыслимое как единое целое” (Г. Кантор – основатель теории множеств).

Определение 2. Задать множество – указать эффективное и недвусмысленное правило, с помощью которого о любом элементе можно сказать: является ли он элементом данного множества.

Комментарий. Эффективность правила означает, что результат его применения достижим за конечное время.

Пример. Множество красивых девушек не является множеством.

Задать множество можно перечислением его элементов (для конечных множеств) или указанием характеристического свойства , то есть такого свойства, которым обладают все элементы задаваемого множества и не обладают никакие элементы никаких других множеств. Обычно множество выделяется из более общего множества, которое называется UNIVERSUM (вселенная) и обозначается буквой U.

На универсуме Uмножества обозначаются кругами, которые называются кругами Эйлера. Множества обозначаются большими буквами латинского алфавита, элементы – соответствующими маленькими (рис.1).

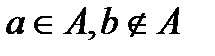
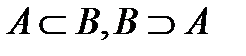
Рис.1Hhhfghfutu6uu1111111111111111111

Знак 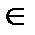означает принадлежность и применяется для элементов, 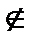– не принадлежать, 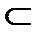– принадлежать для множеств. Множество, не содержащее ни одного элемента, называется пустым и обозначается .

Комментарий. Пустое множество единственно. В самом деле, пусть существуют два разных пустых множества. Это значит, что в одном из них найдется элемент, который не принадлежит другому. Но в пустых множествах нет элементов!

Определение 3. Два множества называются равными, если они состоят из одних и тех же элементов. Обозначается .

Пример. ; но , так как единственным элементом множества является упорядоченная пара , а множество состоит из двух элементов: 1 и 2, и, наконец, это три разных множества.

Определение 4. Множество есть подмножество множества , если справедливо . Обозначается: . Говорят, что множество строго включено во множество , если справедливо, чт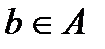о , но .

Комментарий. В функциональном анализе очень часто тот факт, чтомножество есть подмножество множества обозначают .

Определение 5. , если и (т.е. они состоят из одних и тех же элементов).

 

Пример. , так как единственным элементом множества 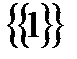является множество .

Определение 6. Рассмотрим множество всех подмножеств конечного множества , то есть содержит пустое множество и само множество . Эти подмножества называются несобственными, а остальные собственными (собственно говоря, они и есть нетривиальные подмножества).

Пример. Пусть , тогда .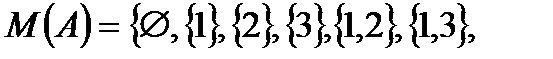

Рис. 2

Определение 7. Объединением множеств и ( (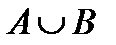читается чашка ) называется новое множество 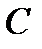, элементами которого являются элементы множества или элементы множества : (рис.2).

Комментарий. Слово “или” употребляется в неразделительном смысле и обозначается значком , который называется дизъюнкция (от лат. disjunctio – разобщение, различие). Тогда .

Аналогично даются определения остальных операций над множествами. Мы их просто выпишем.

Определение

Рис. 3

8. Пересечение: (читается крышка ).

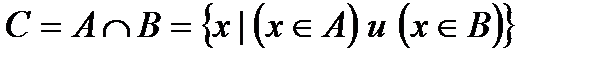(рис.3). Слово “и” обычно заменяют значком - “конъюнкция” (от лат. conjunctio – союз, связь), и тогда множество 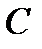описывается так: .

 

Рис. 4

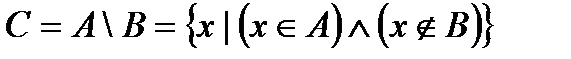Определение 9. Разность: (рис. 4) - все те элементы множества , которые не являются элементами множества .

Рис. 5

Определение 10. Симметрическая разность (дизъюнктивная сумма):

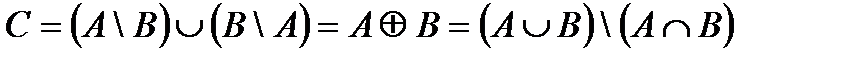(рис.5).

Рис.6

Определение 11. Дополнениеммножества до универсума называется множество, состоящее из всех тех элементов универсума, которые не являются элементами множества (рис. 6). Обозначают .

Определение 12. Функция 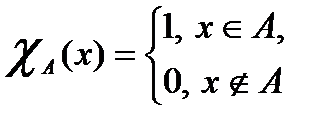называется характеристической функцией множества .

 

Легко составить характеристические функции для всех перечисленных операций. Они называются таблицами Буля. С их помощью легко доказываются свойства операций над множествами.

 

 

U

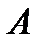
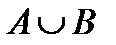
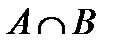
СООТВЕТСТВИЯ

Описания того, что существует хоть в каком – либо

смысле, хоть в каком – либо смысле должны

соответствовать друг другу.

Алекс Алдер.

Комментарий. Соотношения между множествами называются соответствиями. Для определения соответствия надо определить два множества: множество (область) определения и множество (область) значений и указать “пары соответствий”. Соотношения между элементами одного множества называются отношениями между его элементами.

Определение 1. Два элемента одного или разных множеств, расположенные в определенном порядке, называется упорядоченной парой .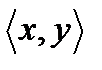

Определение 2. Две упорядоченные пары 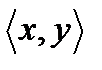и 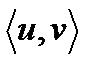равны, если .

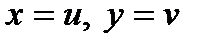Замечание. Естественно, , если .

Замечание. Упорядоченная n-ка (читается энка): .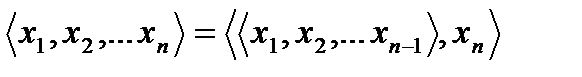

Определение 3. Декартовым (прямым) произведением множеств и 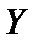(обозначается ) называется множество всех упорядоченных пар 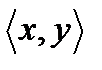таких, что , а . Множество называют областью определения или множеством прообразов, а множество 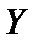– множеством значений или множеством образов.

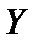Определение 4. Любое подмножество декартова произведения называется бинарным соответствием между множеством и (обозначается ). Если множества и совпадают, то говорят о бинарном отношении.

Пример. Область определения – студенческая группа, сдающая экзамен; множество значений – отл, хор, уд, неуд – множество оценок. Если явились все, то такое соответствие между студентами и их оценками называется всюду определённым, если кто-то не пришёл, то такое соответствие не всюду определённое.

Определение 5. Соответствие функционально (или является функцией), если каждому элементу области определения соответствует не более одного элемента множества значений.

Пример. Соответствие предыдущего примера функционально, потому что каждому студенту соответствует не более одной оценки. Видно, что функцияможетбыть не всюду определена. Если бы за один экзамен студенты могли получать несколько оценок, как, например, в фигурном катании, то соответствие было бы не функционально.

Определение 6. Всюду определённая функция называется отображением, то есть отображение 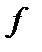из в 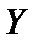(обозначается ) – это правило, которое каждому элементу множества ставит в соответствие единственный элемент множества .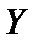

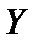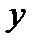
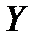Комментарий. При этом двум элементам множества можно ставить в соответствие один и тот же элемент множества . Отображение всегда функционально. Обратное неверно, то есть не всюду определенная функция не является отображением. Отображение можно записать в виде или , где и элементы некоторых множеств , , а 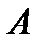заданное отображение. Если и 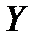числа, то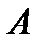 числовая функция, если и 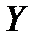векторы или функции, то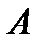 оператор, если векторы или функции, а 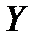числа, то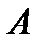 функционал. Иногда понятия отображения и функции не различаются. Тогда отдельно возникает вопрос обобласти определения.

Определение 7. Отображение называется сюръективным, если . Функция называется сюръективной, если каждому соответствует, по крайней мере, один .Таким образом, сюръективным отображением или “ отображением НА” или накрытием множества 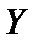называют отображение всего множества на всё множество .

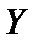Пример. Если сопоставить множество студентов в группе с множеством фамилий в списке группы, с учётом возможных однофамильцев, то это отображение и будет сюръекцией.

Определение 7. Отображение или функциональное соответствие называется инъективным, если каждому образу соответствует единственный прообраз, то есть если . Функция называется инъективной, если каждому 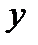из множества соответствует не более одного .

Пример. Если сопоставить множество студентов в группе с множеством фамилий в списке студентов университета и считать, что в группе нет однофамильцев, то такое отображение и называется “отображением В”, или вложением, или инъекцией. То есть разным студентам соответствуют разные фамилии, а в области значений могут быть и “незадействованные фамилии”.

Определение 8. Не всюду определённое функциональное, инъективное соответствие называется взаимно однозначным.

Определение 9. Отображение называется биективным, если каждый элемент множества 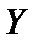поставлен в соответствие ровно одному элементу множества .

Комментарий. Соответствие, которое одновременно всюду определено, функционально, инъективно и сюръективно называется биективным..

Определение 10. Биективное отображение множества в себя называется преобразованием.

Определение 11. Набор преобразований какого-либо множества называется группой, если вместе с любыми двумя преобразованиями он содержит результат их последовательного применения, а вместе с каждым преобразованием - обратное преобразование.

Определение 12. Отображение называется гомоморфизмом, если: каждому элементу и каждому отношению между элементами множества соответствуют один элемент и одно отношение множества 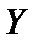(но необязательно наоборот). Если гомоморфизм биективен, он называется изоморфизм. Изоморфизм это отображение, сохраняющее порядок (a < b Û f(a) < f(b)).

Определение 13. Гомеоморфизмом называют частный случай изоморфизма. Два множества гомеоморфны, если существует взаимно однозначное и взаимно непрерывное отображение одного из них на другое.

ОТНОШЕНИЯ

Не относитесь к себе слишком всерьёз.

Пятое правило Черчилля.

(первых четырёх не существует)

Комментарий. Соотношения между элементами одного и того же множества называются отношениями. Отношения характеризуются иным перечнем свойств, нежели соответствия.

Определение 1. На некотором множестве задано отношение , если для любых двух элементов можно сказать, находятся ли они в отношении или нет.

Комментарий. Можно сказать, что отношение есть отображение : , где значение 1 соответствует «истине», а значение 0 — «лжи» (здесь важен порядок, в котором берутся элементы и ).

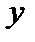Определение 2. Отношение рефлексивно, если .

Комментарий. То есть отношение применимо к самому объекту. Например, отношение включения. Поскольку любое множество включено само в себя, то отношение включения обладает свойством рефлексивности. Отношение «спасения» на множестве утопающих – рефлексивно.

Определение 3. Отношение антирефлексивно, если к самому объекту оно всегда неприменимо.

Например, «перпендикулярность» на множестве прямых. Прямая не может быть перпендикулярна самой себе.
Определение 4. Отношение симметрично, если .

Если Иванов «учится в одной группе» с Петровым, то справедливо и обратное.
Определение 5. Отношение асимметрично, если 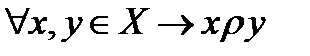, но неверно, что . Если стольник можно “разменять” десятками, то обратное сложно. Определение 6. Отношение антисимметрично, если из и 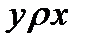следует, что .
Определение 7. Полнота отношения означает, что для любой пары разных элементов данного множества данное отношение выполнимо на всём множестве.

Например, отношение “больше или равно” полно на множестве действительных чисел и не полно на множестве комплексных.
Определение 8. Отношение транзитивно, если из 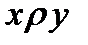и следует, что .

Комментарий. Если Иванов “учится в одной группе” с Петровым, а Петров с Сидоровым, то Иванов “учится в одной группе” с Сидоровым. Отношение включения тоже транзитивно. Если группа «включена» в множество студентов университета, а это множество «включено» в множество студентов страны, то множество студентов группы «включено» в множество студентов страны. Но если студенческую группу рассматривать как элемент университета, понимаемого как множества, состоящего из групп, а университет рассматривать как элемент высшей школы – множества, состоящего из университетов, то группа не является элементом высшей школы (там элементы университеты). То есть отношение “принадлежности” не транзитивно.

Комментарий. Каждое конкретное отношение обладает совокупностью свойств. Рассмотрим важнейшие группы отношений, у которых совокупности свойств одинаковые.

Отношение ЭКВИВАЛЕНТНОСТИ

 

Определение 1. Отношение, обладающее свойствами рефлексивности, симметричности и транзитивности называется отношением эквивалентности.

Комментарий. Это, например, отношение “равенства” чисел, или отношение “учиться в одной студенческой группе”, или отношение изоморфизма. Это определение избыточно потому, что любое симметричное и транзитивное отношение 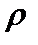рефлексивно. В самом деле, пусть (в силу симметричности). Тогда, в силу транзитивности, имеет место .

Теорема 1. Отношение эквивалентности разбивает множество на непересекающиеся подмножества классы эквивалентности.

Пусть и 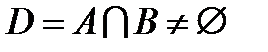. То есть . Тогда и . Отсюда в силу транзитивности , но тогда .■

Определение 2. Множество классов эквивалентности данного множества называется фактор-множеством, а операция построения фактор - множества называется факторизацией.

 

Отношения ПОРЯДКА

Комментарий. Понятия порядка в математике нет, как нет понятия снега в языке чукчей. Это всегда какой-то, вполне определённый порядок.

Определение 1. Отношение, обладающее свойствами асимметричности, антирефлексивности и транзитивности называется отношением строгого порядка.

 

Комментарий. Например, “быть больше” на множестве чисел, “быть после” в очереди, “быть старше”. Это определение избыточно потому, что асимметричность можно показать, но удобно. В самом деле, пусть асимметричность не имеет место, то есть . Тогда из транзитивности имеет место , что противоречит антирефлексивности.

 

Определение 2. Если отношение антисимметрично, рефлексивно и транзитивно, то порядок называют нестрогим, а часто просто порядком. Например, «быть не выше».

 

Определение 3. Если строгий порядок обладают свойством полноты, то есть для любой пары несовпадающих элементов имеет место или , или , то есть, нет несравнимых элементов, то его называют совершенным или линейным, а отношение порождает структуру совершенного строгого порядка.

Определение 4. Если нестрогий порядок обладают свойством полноты, то есть для любой пары элементов имеет место или , или , то есть, нет несравнимых элементов, то его называют совершенным или линейным, а отношение порождает структуру совершенного нестрогого порядка. Порядок называется частичным, если есть несравнимые элементы.

 

Определение 5. Множество , структурированное отношением с совершенным порядком, называется совершенно упорядоченным (частично или строго).

 

Пример. Пусть , тогда 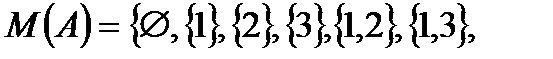. Введём на множестве отношение строгого включения 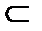. Очевидно, что на множестве существуют несравнимые элементы, например 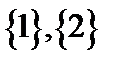, то есть отношение 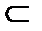не порождает структурусовершенного строгого порядка.

Определение 6. Элемент называется мажорантой множества (если такая существует), если 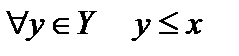, а множество называют ограниченным сверху. Аналогично вводятся миноранта и ограниченное снизу множество.

Определение 7. Миноранта всех мажорант множества (если такая существует), называется супремумом множества и обозначается . Если , то он называется наибольшим элементом множества .

Аналогично вводятся нижняя грань , множества и наименьший элемент множества .

Определение 8. Если множество линейно упорядочено, и, кроме того, в любом его подмножестве можно выделить наименьший элемент, то оно называется вполне упорядоченным.

Определение 9. Любой класс эквивалентности вполне упорядоченных множеств по отношению "изоморфно" называют ординалом.

Пример. Множество натуральных чисел, любая последовательность, любое конечное линейно упорядоченное множество. Множество действительных чисел отрезка [0,1] при естественном способе упорядочения является линейно упорядоченным, но не является вполне упорядоченным, так как не всякое его подмножество имеет наименьший элемент, например, подмножество (0,1].

Бесконечные множества

Бесконечность 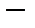это именно то место, где

происходит всё то, чего не может быть.

Алекс Алдер.

 

Определение 1. Множества A и B называются эквивалентными или равномощными, если существует хоть одна биекция f: , то есть отношение равномощности есть отношение эквивалентности.

Комментарий. В качестве эталона можно использовать любоевполне упорядоченное множество, но общепринято использование натурального ряда чисел.

Определение 2. Множество, допускающее биекцию с любым куском натурального ряда чисел 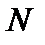, называется конечным. Число элементов в конечном множестве А называют его мощностью. .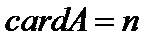

Определение 3. Множество, допускающее биекцию со всем натуральным рядом чисел 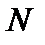называется счетным. Мощность счетного множества называется алеф ноль.

Определение 3. Кардиналами называются классы эквивалентности множеств по отношению "равномощно".

Примеры. Множество целых чисел, множество чётных чисел, множество рациональных чисел, множество чисел вида 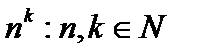, и так далее. Ряд натуральных чисел можно поставить во взаимно однозначное соответствие с рядами квадратов натуральных чисел, степеней двойки, факториалов и т. п.:

1 2 3 4 5 … 1 4 9 16 25 … 2 4 8 16 32 … 1 2 6 24 120

Комментарий. Данное рассуждение демонстрирует нарушение принципа “часть меньше целого” и лежит в основе парадокса Тристрама Шенди, предложенного Расселом в книге “Мистицизм и логика”. В романе Стерна “Жизнь и мнения Тристрама Шенди, джентльмена” герой обнаруживает, что ему потребовался целый год, чтобы изложить события первого дня его жизни, и еще один год понадобился, чтобы описать второй день. То есть материал его биографии накапливается быстрее, чем он сможет его обработать, и он никогда не сможет её завершить. Hо если бы он жил вечно, то события n -го дня Шенди мог бы описать за n -й год. Таким образом, он смог бы описать каждый день, а его жизнь насчитывала бы столько же лет, сколько дней.

Пример. Рассмотрим ещё один факт такого же рода. Построим бесконечное множество следующим образом: на каждом шаге в множество будем добавлять два элемента из натурального ряда