Каждой дуге сети соответствует пропускная способность, указывающая максимальное количество потока, которое можно пропустить через эту дугу. Пусть теперь, кроме того, каждой дуге поставлена в соответствие дуговая стоимость ctj, т. е. стоимость доставки единицы потока из узла Nt в узел Nj. Необходимо найти поток из источника в сток, имеющий заданную величину и обладающий минимальной стоимостью.
Формально задача ставится следующим образом:
минимизировать
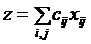
при условиях

При этом подразумевается, что величина v не превышает величины максимального потока из s в t, иначе задача не имеет решения.
Заметим, что если бы не было ограничений на пропускные способности дуг, то достаточно было бы найти самую экономную цепь из s в t и пропустить по ней весь поток. В книге Форда, Фалкерсона «Потоки в сетях» рассматривалось несколько алгоритмов нахождения потока минимальной стоимости, использующих прямо-двойствсппый подход линейного программирования.
Здесь будет рассмотрено два алгоритма, которые не используют понятий линейного программирования и достаточно эффективны в вычислительном отношении.
Первый алгоритм, предложенный Басакером и Гоуэном [22], имеет следующий вид.
Шаг 0. Положить все дуговые потоки и величину потока равными пулю.
Шаг 1. Определить модифицированные дуговые стоимости  , зависящие от величины уже найденного потока, следующим образом:
, зависящие от величины уже найденного потока, следующим образом:

Шаг 2. Найти кратчайшую цепь (т. е. цепь минимальной стоимости) из s в t используя дуговые стоимости  , найденные на шаге 1. Затем пропускать по этой цепи поток до тех пор, пока она не перестанет быть кратчайшей цепью. Получить величину нового потока, прибавив к величине старого величину потока, текущего по рассматриваемой цепи. Если величина итогового потока равна v, то конец. В противном случае перейти к шагу 1.
, найденные на шаге 1. Затем пропускать по этой цепи поток до тех пор, пока она не перестанет быть кратчайшей цепью. Получить величину нового потока, прибавив к величине старого величину потока, текущего по рассматриваемой цепи. Если величина итогового потока равна v, то конец. В противном случае перейти к шагу 1.
Этот алгоритм обладает следующим интересным свойством: каждый раз на шаге 2 получается поток из источника в сток, обладающий минимальной стоимостью. Таким образом, последовательно получаются потоки минимальной стоимости величины р = 1,2,..., v. По этой причине рассмотренный алгоритм можно классифицировать как двойственный.
Второй алгоритм, предложенный Клейном, формулируется следующим образом:
Шаг 1. Найти любой допустимый поток величины v из источника s в сток t. Это может быть сделано подбором или с помощью решения задачи о максимальном потоке (в которой надо проводить вычисления до тех пор, пока величина потока не станет равной v).
Шаг 2. Определить модифицированные стоимости следующим образом:

Шаг 3. Используя величины  , найти в сети цикл отрицательной стоимости (такие циклы для краткости будем называть отрицательными). Если его не существует, то найденный поток является оптимальным. Если же такой цикл найдется, то добавить в сеть поток по нему величины δ, где δ равно минимуму из величин (bij — xij, xji), взятому по дугам отрицательного цикла. Перейти к шагу 2. (Если в сети имеется несколько несвязных отрицательных циклов, то добавляется поток по каждому из них.)
, найти в сети цикл отрицательной стоимости (такие циклы для краткости будем называть отрицательными). Если его не существует, то найденный поток является оптимальным. Если же такой цикл найдется, то добавить в сеть поток по нему величины δ, где δ равно минимуму из величин (bij — xij, xji), взятому по дугам отрицательного цикла. Перейти к шагу 2. (Если в сети имеется несколько несвязных отрицательных циклов, то добавляется поток по каждому из них.)
Так как этот алгоритм с самого начала дает допустимый поток величины и, то его можно классифицировать как прямой алгоритм.
Легко видеть, что оба рассмотренных алгоритма позволяют найти ноток величины v, если это число v не превышает величины максимального потока. Менее очевидно, что эти алгоритмы позволяют найти оптимальный поток. Доказательство этого факта основано на следующей теореме, которая может рассматриваться как основная теорема в теории потоков минимальной стоимости.
Tеорема. Поток величины v оптимален тогда и только тогда, когда в сети с модифицированными дуговыми стоимостями  не существует отрицательных циклов.
не существует отрицательных циклов.
Рассмотрим пример, иллюстрирующий первый алгоритм. Пусть в сети, представленной на рис. 28,первое число около каждой дуги указывает ее пропускную способность, а второе число — ее дуговую стоимость. Все дуги не ориентированы. Надо найти поток величины 2, обладающий минимальной стоимостью.

Рис. 28. Пример к алгоритму Басакера и Гоуэна
Шаг 0. Полагаем все хij = 0.
Шаг 1. Определяем модифицированные стоимости:  = сij.
= сij.
Шаг 2. Находим кратчайшую цепь из s в t используя в качестве длин  = сij. Получаем цепь s, (s; 1), 1, (1; 2), 2, (2; t), t или цепь s, (s; 3), 3, (3; 2), 2, (2; t), t. Выбрав первую цепь, получаем: xs1 = x12 = x2t = 1/
= сij. Получаем цепь s, (s; 1), 1, (1; 2), 2, (2; t), t или цепь s, (s; 3), 3, (3; 2), 2, (2; t), t. Выбрав первую цепь, получаем: xs1 = x12 = x2t = 1/
Шаг 1. Определяем модифицированные стоимости следующим образом:
 =∞, так как xs1=bs1=1,
=∞, так как xs1=bs1=1,
 = -1,
= -1,
 =∞, так как x12=b12=1,
=∞, так как x12=b12=1,
 = -2,
= -2,
 =∞, так как x2t=b2t=1,
=∞, так как x2t=b2t=1,
 =-1,
=-1,
все остальные  = cij.
= cij.
Шаг 2. Находим кратчайшую цепь из s в t, используя в качестве длин новые модифицированные стоимости  .Получаем цепь (s; 3), (3; 2), (2; 1), (1; 4), (4; t)общей стоимости 1 + 2 + (- 2) + 2 + 2 = 5. Пропустив единицу потока по этой цепи, получим окончательно поток, изображенный на рис. 29, где числа около дуг указывают дуговые потоки.
.Получаем цепь (s; 3), (3; 2), (2; 1), (1; 4), (4; t)общей стоимости 1 + 2 + (- 2) + 2 + 2 = 5. Пропустив единицу потока по этой цепи, получим окончательно поток, изображенный на рис. 29, где числа около дуг указывают дуговые потоки.
Этот алгоритм не рекомендуется использовать, когда величина v велика. В этом случае рекомендуется второй алгоритм.

Рис. 29. Результат расчета по алгоритму Басакера и Гоуэна
Рассмотрим пример, иллюстрирующий работу второго алгоритма. Пусть сеть имеет вид, как па рис. 30 (исходные данные взяты из книги Форда, Фалкерсона).

Рис. 30. Пример к алгоритму Клейна
Шаг 1. Используя алгоритм решения задачи о максимальном потоке, находим максимальный поток в сети. Он изображен на рис. 31, где числа указывают дуговые потоки. Жирными линиями выделены дуги минимального разреза.
Для этой цели воспользуемся алгоритмом нахождения кратчайшего расстояния по сети, двойственной исходной, изображенной на рис. 31.

Рис. 31. Результат решения задачи о максимальном потоке
Рис. 32. (s; t) – плоская сеть
Шаг 2. Определяем модифицированные стоимости  .
.
Шаг 3. Каждая дуга минимального разреза оказывается насыщенной, поэтому для нее  =∞. Следовательно, ни одна дуга минимального разреза не может войти в отрицательный цикл. Следовательно, сеть можно разбить на две части и искать отрицательные циклы отдельно в каждой из них. Модифицированные стоимости
=∞. Следовательно, ни одна дуга минимального разреза не может войти в отрицательный цикл. Следовательно, сеть можно разбить на две части и искать отрицательные циклы отдельно в каждой из них. Модифицированные стоимости  в каждой из частей представлены в табл. 10.6 и 10.7.
в каждой из частей представлены в табл. 10.6 и 10.7.
Если применить тернарные операции (1) из § 10.2 к табл. 10.6, то получим отрицательный цикл Л25, Asi, Л12. Добавив bsl — — xsi = 10 единиц потока по этому циклу, получим сеть без отрицательных циклов, т. е. найдем оптимальный поток. Если применить тернарные операции (1) из § 10.2 к табл. 10.2, то обнаружим, что соответствующая сеть не имеет отрицательных циклов, т. е. поток оптимален.

Таблица
Поток минимальной стоимости
Предположим, что задана сеть с пропускными способностями дуг cij. Пусть также для каждой дуги (i; j) заданы число sij, интерпретируемое как затраты (например, затраты на перевозку единицы груза из вершины i в вершину j). Задача поиска потока минимальной стоимости заключается в нахождении для заданной величины j суммарного потока ее распределения по дугам, минимизирующего сумму затрат. Общие методы решения задачи о потоке минимальной стоимости рассматриваются в [8, 37].
Частным случаем задачи о потоке минимальной стоимости является транспортная задача, в которой имеется двудольный граф (двудольным называется граф, множество вершин которого может быть разбито на два непересекающихся подмножества, причем ребра (дуги) графа соединяют вершины только из разных подмножеств), представленный на рис. 26: вершины сети разбиты на две группы – m поставщиков и n потребителей.
Теорема Кёнига: граф является двудольным тогда и только тогда, когда он не содержит циклов нечетной длины (или когда в нем все простые циклы имеют четную длину).
Для поставщиков заданы имеющиеся у них количества единиц товара (груза и т.д.) ai, i =  , для потребителей – требуемые им количества единиц товара bi, i =
, для потребителей – требуемые им количества единиц товара bi, i =  . Также известны затраты sij перевозки единицы товара от i -го поставщика j -му потребителю. Пусть задача является замкнутой, то есть
. Также известны затраты sij перевозки единицы товара от i -го поставщика j -му потребителю. Пусть задача является замкнутой, то есть  =
=  - суммарное предложение равно суммарному спросу (вводя фиктивного поставщика или фиктивного потребителя любую незамкнутую задачу можно свести к замкнутой). Требуется определить потоки товаров от потребителей к поставщикам, минимизирующие суммарные затраты.
- суммарное предложение равно суммарному спросу (вводя фиктивного поставщика или фиктивного потребителя любую незамкнутую задачу можно свести к замкнутой). Требуется определить потоки товаров от потребителей к поставщикам, минимизирующие суммарные затраты.
| Рис. 26. Транспортная задача
| |

Формально транспортную задачу можно записать в виде:

 ®
®  (12)
(12)
 = ai, i =
= ai, i =  (13)
(13)
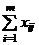 = bj, j =
= bj, j =  . (14)
. (14)
Добавляя к двудольному графу вход «0» и выход «z» и соединяя вход и выход с остальными вершинами дугами с потоком x0i = ai,, i =  , xjz = bj, j =
, xjz = bj, j =  , получаем задачу о потоке минимальной стоимости. Алгоритмы решения транспортной и двойственной к ней задач описаны в [8, 20].
, получаем задачу о потоке минимальной стоимости. Алгоритмы решения транспортной и двойственной к ней задач описаны в [8, 20].
Частным случаем транспортной задачи является задача о назначении, заключающаяся в следующем: имеются n человек (работников), которые могут выполнять различные работы (занимать различные должности), число работ равно числу работников (введя фиктивные должности и/или фиктивные работы, всегда можно незамкнутую задачу привести к рассматриваемой замкнутой форме). Известны затраты sij на назначение i -го работника на j -ю должность (например, минимальная зарплата, за которую он согласится работать на этой должности). Требуется найти назначение работников на должности (каждого работника на одну и только одну должность), минимизирующее суммарные затраты (если sij интерпретируется как эффективность от работы i -го работника на j -ой должности, то оптимальное назначение должно максимизировать суммарную эффективность).
Формально задачу о назначении можно записать в виде (ср. с (12)-(14)):

 ®
®  (15)
(15)
 = 1, i =
= 1, i =  (16)
(16)
 = 1, j =
= 1, j =  . (17)
. (17)
Известны множество методов решения задачи о назначении [8, 20]. Рассмотрим один из них на следующем примере.
Пусть имеются n = 3 работника и столько же работ. Матрица затрат имеет вид:  .
.
Алгоритм 8.
Шаг 0. Назначаем каждого человека на самую дешевую для него работу (назначение выделено на рис. 27 тонкими дугами), то есть положим  =
=  . Если при этом назначение является допустимым (то есть все работы выполняются), то решение получено. Если имеется «дисбаланс», то есть не все работы выполняются ($ j1:
. Если при этом назначение является допустимым (то есть все работы выполняются), то решение получено. Если имеется «дисбаланс», то есть не все работы выполняются ($ j1:  > 1), то переходим к следующему шагу.
> 1), то переходим к следующему шагу.
| Рис. 27. Задача о назначении
| |

Шаг k. Введем два подмножества множества дуг: P1 = {(i; j) | xij = 1 }, P2 = {(i; j) | xij = 0 }. Примем множество вершин-работ, на которых назначено несколько работников за вход сети, множество вершин-работ, которые не выполняются – за выход сети. Изменим направления дуг из множества P1 на обратные и примем их длины равными (-sij), длины дуг из множества P2 примем равными sij. Найдем путь mk минимальной длины в полученной сети (потенциалы вершин, вычисляемые при нахождении кратчайшего пути в рассматриваемом примере, приведены в квадратных скобках). Далее полагаем  =
=  .
.
В результате в рассматриваемом примере за один шаг получим оптимальное назначение, отличающееся от найденного на нулевом шаге тем, что первому работнику назначается третья работа (см. дугу, обозначенную двойными линиями на рис. 27).
На каждом шаге число «дисбалансов» уменьшается на единицу. Следовательно, число шагов алгоритма не превышает числа «дисбалансов», которое конечно.
Аналогичным способом можно решить любую транспортную задачу (искать кратчайший путь из множества вершин, в которые доставили товара больше, чем требуется, во множество вершин, где товара не хватает) [8].
Решение общего случая задачи о потоке минимальной стоимости основывается на рассмотрении двойственной задачи [8, 37].
Псевдопотенциальные графы
Псевдопотенциальный граф - полный (n+1)- вершинный симметричный граф, у которого длина любого гамильтонова контура равна одному и тому же числу.
Обозначим  - длины дуг.
- длины дуг.
Утверждение. Для того, чтобы граф был псевдопотенциальным, необходимо и достаточно существование чисел  ,
,  ,
,  , таких что
, таких что  , для всех i,
, для всех i, 
Кроме того, доказывается, что любой подграф псевдопотенциального графа является псевдопотенциальным.
Механизмы самоокупаемости
В последнее время очень востребованной является технология проектного управления. Рассмотрим случай, когда реализуемый проект состоит из независимых отдельных операций, то есть отдельные этапы реализации этого проекта не связаны технологической последовательность и могут быть реализованы в любом порядке. Естественно возникает вопрос об определении порядка выполнения этапов рассматриваемого проекта. При этом в процессе реализации проекта возникает ситуация, когда приятые меры начинают приносить отдачу в виде денежных поступлений, которые могут быть использованы для выполнения работ по следующим этапам проекта. Если эти средства используются на нужды проекта, то таким образом, проект с какого – то момента времени вступает в режим полного или частичного самофинансирования. Механизмы, обеспечивающие такую ситуацию, получили название механизмов самофинансирования. Очевидно, что размер средств, поступающих для самофинансирования будет зависеть от очередности выполнения работ по проекту. При этом в основу критерия выбора очередности могут быть положены различные критерии. Рассмотрим наиболее характерные постановки задач разработки механизмов самофинансирования проекта, реализуемого одним управляющим центром, как целиком за счет собственных средств, так и с помощью привлечения заемных финансовых ресурсов на весь срок выполнения проекта.
В условиях дефицита свободных оборотных средств, по-прежнему характерного для большей части российской экономики, одной из первостепенных задач управляющего проектом является проблема реализации проекта с привлечением минимальных средств. В том случае, если составные элементы проекта после успешного окончания способны приносить некоторый доход (возможно, не компенсирующий затрат на их выполнение), имеется возможность выбрать план реализации, наиболее эффективно возвращающий этот доход в оборот, то есть в случае нехватки исходных средств некоторые операции могут выполняться за счет доходов от уже выполненных операций. Идеалом, в некотором смысле, является полностью автономный проект, в котором самофинансирование позволяет реализовать его целиком, без привлечения внешних источников. Существенно, что при этом варьируется величина продолжительности проекта.
При разработки механизмов самофинансирования будем пренебрегать возможными технологическими зависимостями между операциями (ограничениями, учитывающими, что i-ая операция не может быть начата до тех пор, пока не завершена (или выполнена на определенный процент объема) j-ая операция или комплекс операций), то есть, считаем, что операции могут выполняться в любой последовательности, и произвольное количество их может выполняться параллельно. Задачи определения оптимальной (с той или иной точки зрения) последовательности операций, связанных технологическими ограничениями, решаются в теории сетевого планирования и управления.
Будем рассматривать региональную администрацию и предприятия, подлежащие реструктуризации как активную систему, состоящую из управляющего органа — центра и n управляемых субъектов - активных элементов, представляющих собой структурные подразделения предприятия. Каждый активный элемент может осуществить некоторое мероприятие (работу в терминах управления проектами), характеризуемое кортежем ( ), где
), где  - затраты, необходимые для начала осуществления i-ой работы,
- затраты, необходимые для начала осуществления i-ой работы,  - доход, получаемый после ее завершения,
- доход, получаемый после ее завершения,  - ее продолжительность,
- ее продолжительность,  = {1, 2,..., n} - множество активных элементов.
= {1, 2,..., n} - множество активных элементов.
Рассмотрим проект, состоящий из n операций, стоимости которых заданы:  . Суммарные затраты в этом случае составляют
. Суммарные затраты в этом случае составляют 
Отметим, что величина  не зависит от взаимного порядка выполнения операций. В том случае, когда центр обладает на момент начала проекта суммой
не зависит от взаимного порядка выполнения операций. В том случае, когда центр обладает на момент начала проекта суммой  , такой что R0 > C0, имеющихся в наличии средств достаточно для выполнения всех операций в любой допустимой последовательности. Если же R0<Co, то возникает задача разработки механизма самофинансирования (самоокупаемости), определяющего оптимальную последовательность выполнения операций, в которой не начатые операции частично финансируются за счет уже выполненных.
, такой что R0 > C0, имеющихся в наличии средств достаточно для выполнения всех операций в любой допустимой последовательности. Если же R0<Co, то возникает задача разработки механизма самофинансирования (самоокупаемости), определяющего оптимальную последовательность выполнения операций, в которой не начатые операции частично финансируются за счет уже выполненных.
Пусть i - ая операция описывается кортежем ( ),
), 
 0 - доход от i-ой операции, а
0 - доход от i-ой операции, а  — ее продолжительность. Поскольку любой проект характеризуется набором обязательных и сопутствующих операций, то естественно, среди необязательных выбираются лишь прибыльные (то есть такие, что
— ее продолжительность. Поскольку любой проект характеризуется набором обязательных и сопутствующих операций, то естественно, среди необязательных выбираются лишь прибыльные (то есть такие, что 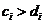 ), а среди операций, обеспечивающих целостность проекта, могут оказаться и убыточные (то есть такие, что
), а среди операций, обеспечивающих целостность проекта, могут оказаться и убыточные (то есть такие, что 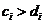 ). В дальнейшем будем различать прибыльные и убыточные операции. Обозначим
). В дальнейшем будем различать прибыльные и убыточные операции. Обозначим  —доход от выполнения i–ой операции. Величина р, может быть, разумеется, как положительной, так и отрицательной.
—доход от выполнения i–ой операции. Величина р, может быть, разумеется, как положительной, так и отрицательной.
Обозначим  - время начала i - ой операции, R- величину заемных средств. Предположим, что имеется возможность получить беспроцентные кредиты в любом объеме, в произвольный момент времени (дисконтирование отсутствует).
- время начала i - ой операции, R- величину заемных средств. Предположим, что имеется возможность получить беспроцентные кредиты в любом объеме, в произвольный момент времени (дисконтирование отсутствует).
Финансовый баланс центра, отражающий текущее соотношение свободных оборотных средств и краткосрочных обязательств, в момент времени t имеет следующий вид:
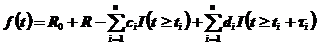
где  .
.
Понятно, что в допустимых вариантах реализации проекта для возможности выполнения операций финансовый баланс должен быть неотрицательным в любой момент времени, то есть для допустимого баланса должно выполняться: f(t)>0,  .
.
В рамках данной модели возникают сразу несколько оптимизационных задач.
Например, можно поставить задачу выбора последовательности выполнения операций (времен их начала), минимизирующей суммарную величину привлеченных средств. Это классическая задача разработки механизмов самофинансирования, единственная из рассматриваемых, для которой существует аналитическое решение (последовательность выполнения операций и величина  ).
).
 (18)
(18)
Отметим также, что в рассмотрении этой задачи нас не интересует насколько велика будет продолжительность проекта, его единственная цель реализовать проект с минимальной суммой денежных средств, которой он располагает в течение всего проекта. В случае если центр будет заинтересован в сокращении срока проекта, это, возможно, приведет к необходимости вложения больших средств, чем это необходимо в условиях задачи (18).
Кроме того, в случае нехватки собственных средств (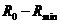 ) центр в условиях задачи (18) обязан привлекать недостающие заемные средства на весь срок проекта.
) центр в условиях задачи (18) обязан привлекать недостающие заемные средства на весь срок проекта.
Другая важная оптимизационная задача, которая может возникнуть перед центром, это минимизация суммарной продолжительности проекта только за счет собственных средств или с фиксированным количеством привлеченных средств. Эта задача имеет обратный характер по отношению к задаче (18), поскольку цели минимизации суммарной величины привлеченных средств и минимизации полной продолжительности проекта вступают в противоречие друг с другом. Отметим, что при последовательном выполнении операций время завершения проекта не зависит от их порядка.
Обозначим  - полную продолжительность проекта.
- полную продолжительность проекта.
Тогда задача минимизации средств затрачиваемых на проект формализуется следующим образом:
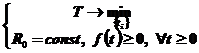 (19)
(19)
Рассмотрим в качестве примера использование для решения задачи минимизации продолжительности проекта следующего эвристического алгоритма.
1. Определяем все комбинации операций, которые могут быть
начаты (являются допустимыми с точки зрения бюджетного ограничения) в нулевой момент времени.
2. Для каждого из допустимых вариантов определяем в момент окончания одной из операций, какие из еще не выполненных
операций могут быть начаты. Если ни одна из операций не может
быть начата, то для данного варианта ждем момента окончания следующей операции и т. д. До тех пор, пока все операции не закончатся и/или ни одна не может быть начата.
Применение шагов 1 и 2 дает все допустимые с точки зрения балансового ограничения варианты (получаем дерево вариантов). Среди висячих вершин могут оказаться и те, которым соответствует выполнение не всех операций. Сравнивая продолжительности тех вариантов - висячих вершин, которые соответствуют выполнению всех операций проекта, определяем варианты минимальной продолжительности.
В общем случае описанный выше алгоритм является более эффективным, чем простой перебор, так как сразу отсеиваются неудовлетворительные варианты и не рассматриваются деревья, для которых они являются корневыми вариантами. Можно предложить и другие эвристические алгоритмы численного решения задачи минимизации средств затрачиваемых на проект, быстродействие которых зависит от соотношения исходных параметров.
Аналитические методы получения оптимального решения существуют лишь для задачи минимизирующей суммарную величину привлеченных средств, алгоритм решения которой описывается в следующей главе.
Быть может, наиболее практически значимой задачей, в том
случае, когда центр заинтересован одновременно в минимизации, как суммарной величины привлеченных средств, так и полной продолжительности проекта, является задача (20). Решение этой задачи позволит определить какой минимальный запас финансовых ресурсов ему необходим, чтобы успешно за вершить проект в заданные сроки.
 (20)
(20)
Таким образом, возможны самые разные постановки. Во всех оптимизационных задачах требуется определить оптимальную последовательность выполнения операций, то есть оптимальный механизм самофинансирования. При введении дисконтирования, по аналогии с задачами (19) и (20) можно максимизировать конечную дисконтированную прибыль и т.д. При наличии технологических ограничений, они должны быть добавлены в ограничения задач (18)-(20).
Необходимо сказать, что на сегодняшний день не существует универсальных и эффективных методов решения задач из рассматриваемого класса. Понятно, что, так как число допустимых вариантов (последовательностей) конечно, то все они могут быть найдены простым перебором. Однако, даже при не очень большом числе операций (порядка нескольких десятков) простой перебор оказывается чрезвычайно трудоемким. Поэтому при решении задачи сетевого планирования используются методы целенаправленного перебора, ветвей и границ и др.
Вообще говоря, для принятия решения о степени финансирования проекта с целью необходимого сокращения срока его продолжительности, необходимо решить задачу (20) для различных значений Т. При этом  , где
, где  - минимальное время продолжительности проекта, а
- минимальное время продолжительности проекта, а  - минимальное время продолжительности проекта, выполненного с привлечением минимума средств (возможно улучшенное, решение задачи (18)). Получив при решении этой задачи набор (Rk, Tk) - оптимальных по Парето сочетаний затраты – продолжительность (то есть в каждом сочетании невозможно уменьшить значение Тк (или Rk), не увеличив одновременно значение
- минимальное время продолжительности проекта, выполненного с привлечением минимума средств (возможно улучшенное, решение задачи (18)). Получив при решении этой задачи набор (Rk, Tk) - оптимальных по Парето сочетаний затраты – продолжительность (то есть в каждом сочетании невозможно уменьшить значение Тк (или Rk), не увеличив одновременно значение 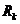 (соответственно Тк)), центр может сделать наилучший выбор, обладая абсолютной полнотой информации.
(соответственно Тк)), центр может сделать наилучший выбор, обладая абсолютной полнотой информации.
Рассмотрим решение задачи о самофинансировании с позиции теории графов.
Рассмотрим (n+1) – вершинный псевдопотенциальный граф с наборами величин  удовлетворяющих условиям теоремы, причем будем считать, что с0=d0=0.
удовлетворяющих условиям теоремы, причем будем считать, что с0=d0=0.
Обозначим  -сумма длин первых j дуг гамильтонова контура
-сумма длин первых j дуг гамильтонова контура 
Введем обозначение для прибыли операции: 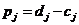
Определим

где 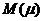 -некоторая характеристика выбранного гамильтонова контура.
-некоторая характеристика выбранного гамильтонова контура.
При сделанных предположениях справедливо следующее утверждение [13]:
Утверждение 2. Существует оптимальное решение задачи
 (21)
(21)
То есть оптимальный контур  , в котором с начала идут вершины с pi ≥0 в порядке возрастания величин ci, а затем вершины с pi ≤ 0 в порядке убывания величин di.
, в котором с начала идут вершины с pi ≥0 в порядке возрастания величин ci, а затем вершины с pi ≤ 0 в порядке убывания величин di.
Пусть  - контур, являющийся решением задачи (21), то есть
- контур, являющийся решением задачи (21), то есть
 j=1,2,…,s, причем
j=1,2,…,s, причем  ,
,  j=s+ 1 ,…,n, причем
j=s+ 1 ,…,n, причем  .
.
Тогда минимальное значение 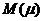 , достигается на оптимальном контуре
, достигается на оптимальном контуре  , сформированным в соответствии с вышеизложенным алгоритмом, равно
, сформированным в соответствии с вышеизложенным алгоритмом, равно
 (22)
(22)
Рассмотрим (n+1)- вершинный граф, в котором вершины 1,2,..., n соответствуют операциям (упорядоченным пола в произвольном порядке), вершина 0 - нулевая операция. Предположим, что с нулевой вершины начинается реализация проекта, ее затраты и доход равны нулю ( ). Пусть
). Пусть  =(0,
=(0,  , 0) - произвольный гамильтонов контур.
, 0) - произвольный гамильтонов контур.
Обозначим  сумма длин первых j дуг контура
сумма длин первых j дуг контура 
Заход некоторой дуги в вершину i (i =  ) требует затрат
) требует затрат  исход дуги из вершины i соответствует получению дохода
исход дуги из вершины i соответствует получению дохода  .Так как в рассматриваемой модели все операции могут выполняться одновременно (не существует технологических ограничений на последовательность их выполнения), то, очевидно, минимуму привлеченных средств будет соответствовать последовательное выполнение операций (время реализации всего проекта равно
.Так как в рассматриваемой модели все операции могут выполняться одновременно (не существует технологических ограничений на последовательность их выполнения), то, очевидно, минимуму привлеченных средств будет соответствовать последовательное выполнение операций (время реализации всего проекта равно  ).
).
а граф, построенный для нашей задачи, будет полным и симметричным.
Таким образом, задача свелась к определению оптимальной последовательности выполнения операций, то есть такой последовательности, при которой величина привлеченных средств будет минимальной. Последовательному выполнению всех операций (ни одна из операций не выполняется дважды) соответствует некоторый гамильтонов контур. Если под длиной дуги  понимать разность между затратами на выполнение j-ой операции и доходом от i- ой операции, то есть
понимать разность между затратами на выполнение j-ой операции и доходом от i- ой операции, то есть  , то легко видеть, что полученный граф является псевдопотенциальным. Действительно, любой гамильтонов контур соответствует выполнению всех операций. Независимо от последовательности суммирования длин дуг, получим инвариантную (не зависящую от последовательности, то есть контура) величину
, то легко видеть, что полученный граф является псевдопотенциальным. Действительно, любой гамильтонов контур соответствует выполнению всех операций. Независимо от последовательности суммирования длин дуг, получим инвариантную (не зависящую от последовательности, то есть контура) величину

Тогда величина 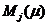 есть взятый с обратным знаком чистый доход от выполнения первых (j-1) операций контура
есть взятый с обратным знаком чистый доход от выполнения первых (j-1) операций контура  и начала j -ой операции.
и начала j -ой операции.
С другой стороны 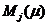 может интерпретироваться как нехватка собственных средств на выполнение j-ой (в контуре
может интерпретироваться как нехватка собственных средств на выполнение j-ой (в контуре  ) операции. Если
) операции. Если  именно такую величину придется занимать у третьей стороны. Если
именно такую величину придется занимать у третьей стороны. Если  то собственных средств хватает на выполнение j-ой операции.
то собственных средств хватает на выполнение j-ой операции.
Предположим теперь, что задача заключается в определении последовательности выполнения операций, при которой максимальная величина однократного займа внешних средств минимальна при условии, что собственные средства отсутствуют (то есть R0=0). Формально эту-задачу можно представить в следующем виде: определить гамильтонов контур  , имеющий минимальное значение
, имеющий минимальное значение


Решение этой задачи дается теоремой 2.
Система неравенств в рассматриваемой модели может интерпретироваться следующим образом. Первое неравенство утверждает, что минимальная величина привлеченных средств не может быть меньше, чем затраты на операцию, выполняемую первой. Действительно, мы предположили, что величина собственных средств равна нулю (если она не равна нулю, то на нее уменьшится Mmin). Следовательно, на первую операцию придется затратить 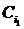 , так как никакие операции еще не выполнялись (нет дохода от их выполнения). Второе неравенство требует, чтобы затраты
, так как никакие операции еще не выполнялись (нет дохода от их выполнения). Второе неравенство требует, чтобы затраты  на выполнение второй операции были меньше, чем заемные средства
на выполнение второй операции были меньше, чем заемные средства  плюс доход
плюс доход  от выполнения первой операции (и т.д. для всех операций).
от выполнения первой операции (и т.д. для всех операций).
Итак, в соответствии с результатом утверждения 2, оптимальное решение имеет следующую структуру:
– упорядочим прибыльные операции (для которых  ) в порядке возрастания затрат (величин
) в порядке возрастания затрат (величин  ) и включим их в последовательность (гамильтонов контур);
) и включим их в последовательность (гамильтонов контур);
– добавим к полученной последовательности убыточные операции (для которых  ) в порядке убывания доходов величин
) в порядке убывания доходов величин  .
.
Таким образом, оптимальной является следующая последовательность: выполнять сначала прибыльные операции в порядке возрастания затрат (сначала наиболее дешевые т.д.), затем выполнять убыточные операции в порядке убывания дохода (сначала приносящие наибольший доход, и т.д.)
В том случае, если, например, найдутся две прибыльные операции с одинаковым параметром значения затрат, совершенно безразлично, какую из двух этих операций выполнять первой, так как при любом порядке их выполнения значение f(t) на отрезке времени, соответствующем выполнению второй операции будет больше, чем для первой, а, следовательно, неважно насколько увеличится финансовый баланс центра в некритический период.
Минимальная величина заемных средств при этом определяется выражением
 (23)
(23)
Содержательная интерпретация этого выражения следующая: как минимум придется занимать либо величину затрат первой операции (если при этом дохода от нее и последующих операций будет хватать на реализацию невыполненных или если объем заемных ср



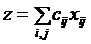

 , зависящие от величины уже найденного потока, следующим образом:
, зависящие от величины уже найденного потока, следующим образом:

 =∞, так как xs1=bs1=1,
=∞, так как xs1=bs1=1, = -1,
= -1, =∞, так как x12=b12=1,
=∞, так как x12=b12=1, = -2,
= -2, =∞, так как x2t=b2t=1,
=∞, так как x2t=b2t=1, =-1,
=-1,




 , для потребителей – требуемые им количества единиц товара bi, i =
, для потребителей – требуемые им количества единиц товара bi, i =  . Также известны затраты sij перевозки единицы товара от i -го поставщика j -му потребителю. Пусть задача является замкнутой, то есть
. Также известны затраты sij перевозки единицы товара от i -го поставщика j -му потребителю. Пусть задача является замкнутой, то есть  =
=  - суммарное предложение равно суммарному спросу (вводя фиктивного поставщика или фиктивного потребителя любую незамкнутую задачу можно свести к замкнутой). Требуется определить потоки товаров от потребителей к поставщикам, минимизирующие суммарные затраты.
- суммарное предложение равно суммарному спросу (вводя фиктивного поставщика или фиктивного потребителя любую незамкнутую задачу можно свести к замкнутой). Требуется определить потоки товаров от потребителей к поставщикам, минимизирующие суммарные затраты.

 ®
®  (12)
(12) = ai, i =
= ai, i = 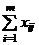 = bj, j =
= bj, j = 
 (15)
(15) = 1, j =
= 1, j =  .
. =
=  . Если при этом назначение является допустимым (то есть все работы выполняются), то решение получено. Если имеется «дисбаланс», то есть не все работы выполняются ($ j1:
. Если при этом назначение является допустимым (то есть все работы выполняются), то решение получено. Если имеется «дисбаланс», то есть не все работы выполняются ($ j1:  > 1), то переходим к следующему шагу.
> 1), то переходим к следующему шагу.
 =
=  .
. - длины дуг.
- длины дуг. ,
,  ,
,  , таких что
, таких что  , для всех i,
, для всех i, 
 ), где
), где  - ее продолжительность,
- ее продолжительность,  = {1, 2,..., n} - множество активных элементов.
= {1, 2,..., n} - множество активных элементов. . Суммарные затраты в этом случае составляют
. Суммарные затраты в этом случае составляют 
 не зависит от взаимного порядка выполнения операций. В том случае, когда центр обладает на момент начала проекта суммой
не зависит от взаимного порядка выполнения операций. В том случае, когда центр обладает на момент начала проекта суммой  , такой что R0 > C0, имеющихся в наличии средств достаточно для выполнения всех операций в любой допустимой последовательности. Если же R0<Co, то возникает задача разработки механизма самофинансирования (самоокупаемости), определяющего оптимальную последовательность выполнения операций, в которой не начатые операции частично финансируются за счет уже выполненных.
, такой что R0 > C0, имеющихся в наличии средств достаточно для выполнения всех операций в любой допустимой последовательности. Если же R0<Co, то возникает задача разработки механизма самофинансирования (самоокупаемости), определяющего оптимальную последовательность выполнения операций, в которой не начатые операции частично финансируются за счет уже выполненных. ),
), 
 0 - доход от i-ой операции, а
0 - доход от i-ой операции, а 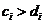 ), а среди операций, обеспечивающих целостность проекта, могут оказаться и убыточные (то есть такие, что
), а среди операций, обеспечивающих целостность проекта, могут оказаться и убыточные (то есть такие, что  —доход от выполнения i–ой операции. Величина р, может быть, разумеется, как положительной, так и отрицательной.
—доход от выполнения i–ой операции. Величина р, может быть, разумеется, как положительной, так и отрицательной. - время начала i - ой операции, R- величину заемных средств. Предположим, что имеется возможность получить беспроцентные кредиты в любом объеме, в произвольный момент времени (дисконтирование отсутствует).
- время начала i - ой операции, R- величину заемных средств. Предположим, что имеется возможность получить беспроцентные кредиты в любом объеме, в произвольный момент времени (дисконтирование отсутствует).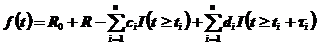
 .
. .
. ).
). (18)
(18)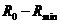 ) центр в условиях задачи (18) обязан привлекать недостающие заемные средства на весь срок проекта.
) центр в условиях задачи (18) обязан привлекать недостающие заемные средства на весь срок проекта. - полную продолжительность проекта.
- полную продолжительность проекта.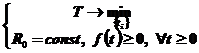 (19)
(19) (20)
(20) , где
, где  - минимальное время продолжительности проекта, а
- минимальное время продолжительности проекта, а  - минимальное время продолжительности проекта, выполненного с привлечением минимума средств (возможно улучшенное, решение задачи (18)). Получив при решении этой задачи набор (Rk, Tk) - оптимальных по Парето сочетаний затраты – продолжительность (то есть в каждом сочетании невозможно уменьшить значение Тк (или Rk), не увеличив одновременно значение
- минимальное время продолжительности проекта, выполненного с привлечением минимума средств (возможно улучшенное, решение задачи (18)). Получив при решении этой задачи набор (Rk, Tk) - оптимальных по Парето сочетаний затраты – продолжительность (то есть в каждом сочетании невозможно уменьшить значение Тк (или Rk), не увеличив одновременно значение 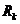 (соответственно Тк)), центр может сделать наилучший выбор, обладая абсолютной полнотой информации.
(соответственно Тк)), центр может сделать наилучший выбор, обладая абсолютной полнотой информации. удовлетворяющих условиям теоремы, причем будем считать, что с0=d0=0.
удовлетворяющих условиям теоремы, причем будем считать, что с0=d0=0. -сумма длин первых j дуг гамильтонова контура
-сумма длин первых j дуг гамильтонова контура 
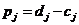

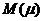 -некоторая характеристика выбранного гамильтонова контура.
-некоторая характеристика выбранного гамильтонова контура. (21)
(21) , в котором с начала идут вершины с pi ≥0 в порядке возрастания величин ci, а затем вершины с pi ≤ 0 в порядке убывания величин di.
, в котором с начала идут вершины с pi ≥0 в порядке возрастания величин ci, а затем вершины с pi ≤ 0 в порядке убывания величин di. j=1,2,…,s, причем
j=1,2,…,s, причем  ,
,  j=s+ 1 ,…,n, причем
j=s+ 1 ,…,n, причем  .
. , сформированным в соответствии с вышеизложенным алгоритмом, равно
, сформированным в соответствии с вышеизложенным алгоритмом, равно (22)
(22) ). Пусть
). Пусть  , 0) - произвольный гамильтонов контур.
, 0) - произвольный гамильтонов контур. сумма длин первых j дуг контура
сумма длин первых j дуг контура  ) требует затрат
) требует затрат  ).
). понимать разность между затратами на выполнение j-ой операции и доходом от i- ой операции, то есть
понимать разность между затратами на выполнение j-ой операции и доходом от i- ой операции, то есть  , то легко видеть, что полученный граф является псевдопотенциальным. Действительно, любой гамильтонов контур соответствует выполнению всех операций. Независимо от последовательности суммирования длин дуг, получим инвариантную (не зависящую от последовательности, то есть контура) величину
, то легко видеть, что полученный граф является псевдопотенциальным. Действительно, любой гамильтонов контур соответствует выполнению всех операций. Независимо от последовательности суммирования длин дуг, получим инвариантную (не зависящую от последовательности, то есть контура) величину
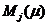 есть взятый с обратным знаком чистый доход от выполнения первых (j-1) операций контура
есть взятый с обратным знаком чистый доход от выполнения первых (j-1) операций контура  именно такую величину придется занимать у третьей стороны. Если
именно такую величину придется занимать у третьей стороны. Если  то собственных средств хватает на выполнение j-ой операции.
то собственных средств хватает на выполнение j-ой операции.

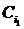 , так как никакие операции еще не выполнялись (нет дохода от их выполнения). Второе неравенство требует, чтобы затраты
, так как никакие операции еще не выполнялись (нет дохода от их выполнения). Второе неравенство требует, чтобы затраты  на выполнение второй операции были меньше, чем заемные средства
на выполнение второй операции были меньше, чем заемные средства  плюс доход
плюс доход  от выполнения первой операции (и т.д. для всех операций).
от выполнения первой операции (и т.д. для всех операций). ) в порядке возрастания затрат (величин
) в порядке возрастания затрат (величин  ) в порядке убывания доходов величин
) в порядке убывания доходов величин 


