Задачи поиска кратчайших и длиннейших путей на графах возникают в различных областях управления. Сначала мы рассмотрим задачи о кратчайшем пути, затем задачи об экстремальных контурах.
Задача о кратчайшем пути
Пусть задана сеть из n+1 вершины, то есть ориентированный граф, в котором выделены две вершины - вход (нулевая вершина) и выход (вершина с номером n). Для каждой дуги заданы числа, называемые длинами дуг. Длиной пути (контура) называется сумма длин входящих в него дуг (если длины дуг не заданы, то длина пути (контура) определяется как число входящих в него дуг). Задача заключается в поиске кратчайшего пути (пути минимальной длины) от входа до выхода сети.
Теорема 1 [8]. Для существования кратчайшего пути необходимо и достаточно отсутствия в сети контуров отрицательной длины.
Предположим, что в сети нет контуров. Тогда всегда можно пронумеровать вершины таким образом, что для любой дуги (i, j) имеет место j > i. Такая нумерация называется правильной.
Известно, что в сети без контуров всегда существует правильная нумерация.
Обозначим lij – длину дуги (i; j). Кратчайший путь в сети, имеющей правильную нумерацию, определяется следующим алгоритмом.
Алгоритм 1.
Шаг 0: Помечаем нулевую вершину индексом l0 = 0;
Шаг k: помечаем вершину k индексом lk =  (li + lik).
(li + lik).
Индекс выхода ln будет равен длине кратчайшего пути.
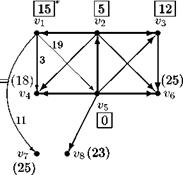
Пример Рассмотрим работу алгоритма определения кратчайшего пути для сети изображенной на рис. 12 (числа у дуг равны длинам дуг, индексы вершин помещены в квадратные скобки, кратчайший путь выделен двойными линиями).
Шаг 0. Вершине 0 присваиваем индекс равный 0.
Шаг 1. Рассматриваем вершину 1. Индекс вершины равен
λ1 =min(λ0 +l01)=0+3=3
| Рис. 12. Поиск кратчайшего пути
| |

Шаг 2. Рассматриваем вершину 1. Индекс вершины равен
λ1 =min(λ0+l01)=0+3=3
Шаг 3. Рассматриваем вершину 3. Индекс вершины равен
λ3 =min(λ1+l13; λ2+l23)=min(3+8;8+2)=10
Шаг 4. Рассматриваем вершину 4. Индекс вершины равен
λ4 =min(λ2 +l24)=8+1=9
Шаг 5. Рассматриваем вершину 5. Индекс вершины равен
λ5 =min(λ3 +l35; λ4 +l45)=min(10+4;9+6)=14
Когда индексы (называемые в некоторых задачах потенциалами вершин) установятся, кратчайший путь определяется методом обратного хода от выхода к входу, то есть кратчайшим является путь m = (0; i1; i2;...; in-1; n), такой, что  = ln - ln-1 и т.д.
= ln - ln-1 и т.д.
Осуществляя обратный ход для рассматриваемого примера получаем:
λ5= λ3+l35;
λ3= λ2+l23;
λ2= λ1+l12;
λ1= λ0+l01;
Таким образом, кратчайший путь проходит через вершины:
0→1→2→3→5
и имеет длину равную 14.
Следующий алгоритм дает возможность определять кратчайший путь в общем случае (то есть при произвольной нумерации вершин).
Алгоритм 2 (алгоритм Форда).
Шаг 0: Помечаем нулевую вершину индексом l0 = 0, все остальные вершины индексами li = +¥, i =  ;
;
Шаг k: Рассматриваем все дуги. Для дуги (i; j), если lj - li >lij, то вычисляем новое значение  = li + lij.
= li + lij.
Индексы устанавливаются за конечное число шагов. Обозначим {  } – установившиеся значения индексов, которые обладают следующим свойством: величина
} – установившиеся значения индексов, которые обладают следующим свойством: величина  равна длине кратчайшего пути из нулевой вершины в вершину i. Кратчайший путь из вершины 0 в вершину i определяется методом обратного хода.
равна длине кратчайшего пути из нулевой вершины в вершину i. Кратчайший путь из вершины 0 в вершину i определяется методом обратного хода.
Пример. Рассмотрим пример работы алгоритма Форда для сети с произвольной нумерацией вершин для сети изображенной на рис. 13.
| Рис. 13. Поиск кратчайшего пути для алгоритма Форда
| |

Шаг 0. λ0=0; λ1=∞; λ2=∞; λ3=∞; λ4=∞; λ5=∞.
Шаг 1. Рассматриваем дугу (0;1). Вычисляем соотношение λ1 – λ0=∞. Проверяем выполнение условия (λ1 – λ0)>l01. Соотношение выполняется, поэтому вычисляем новое значение λ1
λ1=(λ0 +l01)=0+3=3
Шаг 2. Рассматриваем дугу (0;2). Вычисляем соотношение λ2 – λ0=∞. Проверяем выполнение условия (λ2 – λ0)>l01. Соотношение выполняется, поэтому вычисляем новое значение λ2: λ2=(λ0 +l02)=0+9=9
Шаг 3. Рассматриваем дугу (1;3). Вычисляем соотношение λ3 – λ1=∞. Проверяем выполнение условия (λ3 – λ1)>l13. Соотношение выполняется, поэтому вычисляем новое значение λ3: λ3=(λ1 +l13)=3+8=11
Шаг 4. Рассматриваем дугу (3;2). Вычисляем соотношение λ2 – λ3=9 – 11= - 3. Проверяем выполнение условия (λ2 – λ3)>l32. Соотношение не выполняется, поэтому новое значение λ2 не вычисляется.
Шаг 5. Рассматриваем дугу (2;1). Вычисляем соотношение λ1 – λ2=3 – 9= - 6. Проверяем выполнение условия (λ1 – λ2)>l21. Соотношение не выполняется, поэтому новое значение λ1 не вычисляется.
Шаг 6. Рассматриваем дугу (2;4). Вычисляем соотношение λ4 – λ2=∞. Проверяем выполнение условия (λ4 – λ2)>l24. Соотношение выполняется, поэтому вычисляем новое значение λ4: λ4=(λ2 +l24)=9+1=10
Шаг 7. Рассматриваем дугу (3;5). Вычисляем соотношение λ5 – λ3=∞. Проверяем выполнение условия (λ5 – λ3)>l35. Соотношение выполняется, поэтому вычисляем новое значение λ5: λ5=(λ3 +l35)=11+4=15
Шаг 8. Рассматриваем дугу (4;5). Вычисляем соотношение λ5 –λ4=15 – 10 =5. Проверяем выполнение условия (λ5 – λ3)>l01. Соотношение не выполняется, поэтому новое значение λ5 не вычисляется.
Обратным ходом получаем кратчайший путь 5→3→1→0
Если длины всех дуг неотрицательны, то для поиска кратчайшего пути примен и м следующий алгоритм.
Алгоритм 3 (алгоритм Данцига).
Шаг 0: Помечаем нулевую вершину индексом l0 = 0;
Шаг k: Пусть уже помечено некоторое множество вершин. Обозначим Q – множество непомеченных вершин, смежных с помеченными. Для каждой вершины k Î Q вычисляем величину xk = min (lk + lki), где минимум берется по всем помеченным вершинам i, смежным с вершиной k. Помечаем вершину k, для которой величина xk минимальна, индексом lk = xk.
Подобную процедуру повторяем до тех пор, пока не будет помечена вершина n. Длина кратчайшего пути равна ln, а сам кратчайший путь определяется так, как это было описано выше.
Пример алгоритма Данцига
Позволяет найти кратчайший путь между некоторой вершиной s и остальными вершинами при условии, что в графе нет дуг (ребер) с отрицательным весом. Рассмотрим основную идею алгоритма на примере графа на рис. 1 с матрицей смежности С. Пустые клетки означают, что соответствующих дуг в графе нет. Можно считать также, что дуги есть и каждая имеет вес равный ∞). В качестве начальной возьмем вершину v 5.
|
| v1
| v
| v3
| v4
| v5
| v6
| v7
| v8
| v9
| v10
|
| v1
|
|
|
|
|
|
|
|
|
|
|
| v2
|
|
|
|
|
|
|
|
|
|
|
| v3
|
|
|
|
|
|
|
|
|
|
|
| v4
|
|
|
|
|
|
|
|
|
|
|
| v5
|
|
|
|
|
|
|
|
|
|
|
| v6
|
|
|
|
|
|
|
|
|
|
|
| v7
|
|
|
|
|
|
|
|
|
|
|
| v8
|
|
|
|
|
|
|
|
|
|
|
| v9
|
|
|
|
|
|
|
|
|
|
|
| v10
|
|
|
|
|
|
|
|
|
|
|
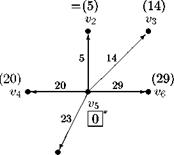 Выделим все вершины смежные рассматриваемой, то есть вершине v5и припишем им числовые метки l (vi), равные весам дуг (v 5 ,vi), как показано на рис. 2 (веса проставлены около дуг, а метки - около вершин и заключены в круглые скобки). Очевидно, что кратчайший путь до v2состоит из единственной дуги (v 5, v 2), а его длина l (v 2)=5.
Выделим все вершины смежные рассматриваемой, то есть вершине v5и припишем им числовые метки l (vi), равные весам дуг (v 5 ,vi), как показано на рис. 2 (веса проставлены около дуг, а метки - около вершин и заключены в круглые скобки). Очевидно, что кратчайший путь до v2состоит из единственной дуги (v 5, v 2), а его длина l (v 2)=5.
Рис. 2
Зафиксируем эту вершину и будем считать ее метку постоянной. Таким образом, для v 2 задача решена. Относительно остальных четырех вершин можно лишь утверждать, что длины кратчайших путей до них не превосходят значений l (vi). Поэтому соответствующие метки пока считаем временными. В дальнейшем, чтобы различать постоянные и временные метки постоянные будем заключать в рамку.
Выделим все вершины смежные v2. Таких четыре v 1, v 3, v 4, v 6и рассмотрим дуги (v 2, vi)изображенные на рис. 3. Поскольку l (v2)+ c (v 2, v 3 )<l( v3 ), "обходной" путь v 5 →v 2→ v 3 короче чем «прямой»
.
Рис. 3
(v5 → v3), поэтому за новое значение метки l(v3) примем сумму
l (v2) +c (v2,v 3)=12.
Аналогичной проверкой устанавливаем, что прямой путь (v5 → v4) короче, чем обходной v 5 →v 2→ v 4, следовательно значение метки l(v4) сохраняется прежним. Для вершины v6, как и для v3, метка корректируется и принимает значение 27. Кроме вершин v3, v 4 и v 6, достижимых из v5 непосредственно, есть еще одна вершина v1, единственный путь к которой лежит через постоянно помеченную v2. Поэтому в качестве значения метки для нее естественно вять сумму l(v2)+c(v2,v1). Будем говорить что теперь метки l(v 1 ),l(v3) и l(v6) получены из вершины v2. Из пяти временных меток минимальной является l(v3)=12, которая и определяет длину кратчайшего пути до v3. Так как метка получена из v2, путь имеет вид v5→v 2 →v3. Таким образом, задача решена идля v3, которая становится постоянно помеченной. Этот факт отражен на рис. 4.
Рис. 4
Кроме уже рассмотренных дуг, изображена и единственная дуга, выходящая из v3. Наличие этой дуги требует пересчета значения метки l(v6). Так как l ( v3 )+c( v3, v6)<27, за новое значение l(v6)примем сумму l (v3) +c (v3, v6)=25. Минимальной среди временных меток является l (v1) = 15. Это значит, что выявлен кратчайший путь v5→v2→v1, а метка вершины v 1 становится постоянной. Последующие действия выполняются аналогично. Для v 1, как последней постоянно помеченной находим множество смежных еще непомеченных вершин v 4, v 5, v 7и анализируем их метки, принимая во внимание длины дуг, связывающих v 1 с этими вершинами. Так как l (v 1) +c (v 1, v 4)< l (v 4), метка вершины v 4 корректируется, становясь равной 18.
Рис. 5
У вершины v 5 метка постоянная и поэтому не меняется. Наконец, v 7, до этого не рассматривавшаяся, получает начальную метку равную l (v 1) +c (v 1, v 7) =25. Граф, отражающий ситуацию, представ лен на рис. 5. Здесь минимальной временной меткой оказывается d (v 4)=18. Теперь вершина v 4 становится постоянно помеченной. Так как вою метку она получила из v 1, кратчайший путь к ней со стоит из кратчайшего пути до v 1 и дуги (v 1, v 4) и выглядит так v5 → v 2→ v 1→ v 4, а его длина равна 18.
Итерационный процесс продолжается до тех пор, пока конечная вершина искомого кратчайшего пути не станет постоянно помеченной. Если же требуется найти кратчайшие пути до всех вершин, итерации выполняются пока все вершины не получат постоянные метки.
Обработку данных в соответствии с алгоритмом целесообразно оформлять в виде таблицы, строки которой соответствуют итерациям, а столбцы - вершинам графа и отражают процесс изменения их временных меток вплоть до момента, когда временная метка становится постоянной. Два дополнительных столбца таблицы нужны, чтобы зафиксировать вершину, которая становится постоянно помеченной на очередной итерации и длину кратчайшего пути до этой вершины
В табл. 2 содержатся результаты расчетов для разобранного выше примера Покажем, как она заполняется.
Таблица 2
| Итерация
| v1
| v2
| v3
| v4
| v5
| v6
| v7
| v8
| v9
| v10
| p
| l(p)
|
1
|
|
|
|
|
|
|
|
|
|
| v5
| 0
|
|
|
|
|
|
|
|
|
|
|
|
| v2
|
|
|
|
|
|
|
|
|
|
|
|
|
| v 3
|
|
|
|
|
|
|
|
|
|
|
|
|
| v1
|
|
|
|
|
|
|
|
|
|
|
|
|
| v4
|
|
6
|
|
|
|
|
| 25
| 23
|
|
|
| v8
| 21
|
|
|
|
|
|
|
|
|
|
|
|
| v7
|
|
|
|
|
|
|
|
|
|
|
|
|
| v 6
|
|
|
|
|
|
|
|
|
|
|
|
|
| v9
|
|
|
|
|
|
|
|
|
|
|
|
|
| v10
|
|
| пред
| v 2
| v 5
| v 2
| vч
| v 5
| vз
| v
| v
| vб
| vб
|
|
|
На первой итерации полагаем временные метки для всех вершин, кроме начальной, равными ∞, а для начальной – 0. Последней постоянно помеченной считаем вершину v 5, а, е метку равной 0.
На второй итерации, используя матрицу С, находим все вершины смежные с вершиной v 5 и перечитываем их временные метки по формуле l (vi) =min { l (vi), l (vp) +c (vp, v i)}. Среди временных меток ищем минимальную. Это метка вершины v2, теперь ее считаем постоянно помеченной.
На третьей итерации находим вершины смежные с v2 и пересчитываем их временные метки. Среди всех временных вновь ищем минимальную метку. На этой итерации постоянно помеченной становится вершина v3, и т.д.
Процесс заканчивается на десятой итерации, когда постоянную метку получает v10. Результаты - длины кратчайших путей - содержатся в двух последних столбцах таблицы.
Чтобы находить сами пути, сформируем еще одну строчку таблицы (пред), в которой для каждой вершины графа указана ее предшественница на кратчайшем пути. С этой целью в каждом столбце отыскиваем самую нижнюю строку с предпоследним значением метки. Например, в первом столбце это вторая строка, в восьмом - пятая. Искомая вершина-предшественница содержится в столбце p найденной строки. Для v 1 это вершина v2, а для v 8 - вершина v 4. Теперь для определения самого пути достаточно записать цепочку вершин-предшественниц начиная с конечной вершины. Так для v 10 имеем: v 6, v 3, v 2, v 5. Это значит, что кратчайший путь между v 5 v 10 имеет вид v 5 v 2 v 3 v 6 v 10.



 (li + lik).
(li + lik).
 = ln - ln-1 и т.д.
= ln - ln-1 и т.д. ;
; = li + lij.
= li + lij. } – установившиеся значения индексов, которые обладают следующим свойством: величина
} – установившиеся значения индексов, которые обладают следующим свойством: величина 

 Выделим все вершины смежные рассматриваемой, то есть вершине v5и припишем им числовые метки l (vi), равные весам дуг (v 5 ,vi), как показано на рис. 2 (веса проставлены около дуг, а метки - около вершин и заключены в круглые скобки). Очевидно, что кратчайший путь до v2состоит из единственной дуги (v 5, v 2), а его длина l (v 2)=5.
Выделим все вершины смежные рассматриваемой, то есть вершине v5и припишем им числовые метки l (vi), равные весам дуг (v 5 ,vi), как показано на рис. 2 (веса проставлены около дуг, а метки - около вершин и заключены в круглые скобки). Очевидно, что кратчайший путь до v2состоит из единственной дуги (v 5, v 2), а его длина l (v 2)=5.