

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...
Топ:
Оснащения врачебно-сестринской бригады.
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении...
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Интересное:
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Какими должны быть абсолютные или относительные погрешности аргументов функций, чтобы ее абсолютная или относительная погрешность не превышала какой-то заданной величины.
Пусть  непрерывно дифференцируема в области
непрерывно дифференцируема в области 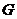 и точка
и точка  вместе параллелепипедом
вместе параллелепипедом 
С какой точностью следует взять приближение  аргументов
аргументов 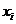 , чтобы приближение
, чтобы приближение  функции
функции  удовлетворяло:
удовлетворяло: 
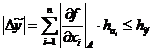

Существуют различные подходы к решению этой задачи. Один из них называется принципом равных влияний. Он заключается в следующем:
- предполагается, что погрешности всех аргументов вносят одинаковые доли в погрешность функции, т.е. что все частные дифференциалы равны между собой по модулю.
В этом случае 
Иногда при решении обратной задачи предполагают, что погрешности всех аргументов равны 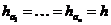
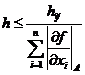
Пример:
С каким числом десятичных знаков следует представить дроби, чтобы сумма их была найдена с точностью до 0,001.
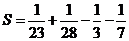


С какой погрешностью нужно взять аргументы 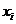 , чтобы
, чтобы 


Поскольку нам необходимо  с недостатком, поэтому мы имеем дело с величиной
с недостатком, поэтому мы имеем дело с величиной  следовательно для достижения цели задачи необходимо в аргументах функции оставлять 4 цифры после запятой.
следовательно для достижения цели задачи необходимо в аргументах функции оставлять 4 цифры после запятой.
Метод границ
Существуют различные способы оценки точности приближ. знач.:
1) метод строгого учета погрешн.
2)приближ. вычисл. без учета погрешн.
3)метод границ
Метод границ позволяет установить границы в кот. закл. знач. выполняемое по ф-ле, если известны границы парам., входящих в эту же ф-лу. Пусть Х-нек. число, нижняя граница НГх, верх. граница Х ВГх, НГх≤х≤ ВГх, НГy≤х≤ ВГy справедлива теор. 1:
Теорема 1
Сумма нижн. границ слаг. явл. нижн. границей суммы слаг. Сумма верх. границ слаг. явл. верх. границей суммы слаг.
|
|
Теорема 2
НГх-у= НГх- ВГy, ВГх-у= ВГх- НГy.
Док-во:
НГх- НГy≤х-у≤ ВГх- ВГy т.о.
НГх-у =НГх- НГy
ВГх-у = ВГх- ВГy
Пример
5.7≤х≤8.4 9≤х+у≤13.8
3.3≤у≤5.4 0.3≤х-у≤5.1
Теорема 3: Если нижние границы сомнож. неотриц., то справедливо след.: НГх* НГy≤ху≤ ВГх* ВГy.
Теорема 4: Если нижн. Граница х неотриц. и n-целое полож. число, то нижн. граница  =(
=( 
 =(
=(
Теорема 5: Если нижн. границах неотриц., то  =
=  и
и  =
= 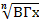
Теорема 6: Если нижняя граница делителя полож., то  ≤
≤  ≤
≤  . Док-во:
. Док-во:  ≤
≤  ≤
≤ 
Пример: Найти А= 
2.57≤х≤2.58;1.45≤у≤1.46;8.33≤z≤8.34 (табл.).
8. Математические модели и численные методы.Вспомогательные сведения из математического анализа. Метод оптимального исключения решения СЛАУ.
Бол-во физ. задач решаются при помощи мат. Знаков один из методов решения таких задач-это эксперимент.Второй-матем. исследование физ. Явления.Такое исслдед. применяется не к реал. Физ. процессу, а к его мат. модели.первая стадия при решении задачи – это постановка задачи или формул- мат. модели.2-ая задача – матем. Модели в завис. От её применения.Числ. методы делятся на:
- точные(дают решение задачи через конечное число арифм. Действий причём, если
исх. данные известны точно и вычисл. производ. без округл., то и вычисл. произв. точно-м. Гауса,Крамера и процесс ортогонализации)
- приближённые или итерационные методы (дают бескон. послед. приближенный, предел кот. если он Э явл. решением задачи – метод простой итерации, метод касат. реш.ур-ний и сист. ур-ний метод секущих, метод Зейделя.
Мн-во х произв.эл-ов наз. метрическим пр-вам, если любым эл-ам х,у став. в соотв. 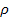 (х,у) наз.расст.между х,у (метрикой) удовл.след.условиям:
(х,у) наз.расст.между х,у (метрикой) удовл.след.условиям:
1)  (х,у)
(х,у) 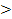 0 и
0 и 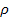 (х,у)=0 если х=у
(х,у)=0 если х=у
2)  (х,у)=
(х,у)=  (у,х)
(у,х)
3)  (х,z)
(х,z)
Послед. {хn 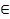 cх}наз.сходящейся если к х*
cх}наз.сходящейся если к х* 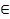 х если метрика между
х если метрика между 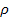 {хn,xm}
{хn,xm} 
Метр.пр-во в коп. всякая фунд.послед.сходится наз.полным.
Пусть х,у-метр.пр-ва,отображение f:х  Y наз.оператором заданное в х со знач.у,то f-отображ.метрич.пр-во на себя.Если f(х)=х,где х
Y наз.оператором заданное в х со знач.у,то f-отображ.метрич.пр-во на себя.Если f(х)=х,где х 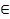 х,то х-неподвиж.точка отображ. f. Метод оптимального исключения по существу является вариацией метода Гаусса. Идея этого метода состоит в том, что последовательным исключением неизвестных матрица системы приводится к диагональному виду. Возможность же таких эквивалентных преобразований следует из теоремы о приведении матрицы к диагональному виду.
х,то х-неподвиж.точка отображ. f. Метод оптимального исключения по существу является вариацией метода Гаусса. Идея этого метода состоит в том, что последовательным исключением неизвестных матрица системы приводится к диагональному виду. Возможность же таких эквивалентных преобразований следует из теоремы о приведении матрицы к диагональному виду.
|
|
Теорема. Для любой квадратной вещественной матрицы А л-го порядка существуют такие квадратные вещественные матрицы и и v (п-го порядка), что матрица UAV - диагональная. (см. с. 29).
|
|
|

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!