maτ=∑Fin
υ2\ρ=ρ∑Fin
0=∑Fib
Проекция на 3. на Mτnb: m*dv/dt=ΣFkτ, m*dv/dt=ΣFkn, m*dv/dt=ΣFkb
37. Относительное движение материальной точки. Дифференциальные уравнения относительного движения точки. Переносная и кориолисова силы инерции. Частные случаи относительного движения точки.
| Динамика относительного движения материальной точки
| След.»
|
|
Второй закон динамики и полученные на его основе уравнения и теоремы верны только для так называемого абсолютного движения точки, то есть движения по отношению к инерциальной (неподвижной) системе отсчета.
Изучим движение материальной точки относительно неинерциальной системы отсчета, то есть подвижной системы отсчета. Рассмотрим материальную точку 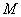 , движущуюся под действием приложенных к ней сил , движущуюся под действием приложенных к ней сил 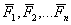 , являющихся результатом взаимодействия точки с другими телами. Будем изучать движение этой точки по отношению к осям , являющихся результатом взаимодействия точки с другими телами. Будем изучать движение этой точки по отношению к осям 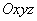 , которые в свою очередь каким-то известным нам образом движутся относительно инерциальной системы отсчета (неподвижных осей) , которые в свою очередь каким-то известным нам образом движутся относительно инерциальной системы отсчета (неподвижных осей) 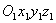 (рис.1). (рис.1).
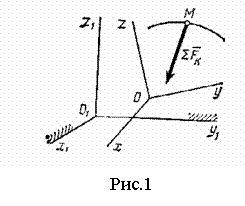 Движение точки
Движение точки 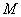 относительно системы относительно системы  называется абсолютным, а движение этой точки относительно системы называется абсолютным, а движение этой точки относительно системы  - относительным. Движение подвижной системы - относительным. Движение подвижной системы 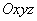 относительно неподвижной системы относительно неподвижной системы 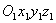 называется переносным движением.
Считая, что переносное движение системы называется переносным движением.
Считая, что переносное движение системы 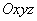 и система сил и система сил 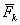 известны, основное уравнение динамики для абсолютного движения точки известны, основное уравнение динамики для абсолютного движения точки 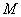 запишется в виде запишется в виде
|
| 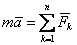
| (1)
| где 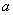 - абсолютное ускорение точки - абсолютное ускорение точки  , а , а 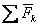 - геометрическая сумма приложенных к точке сил. - геометрическая сумма приложенных к точке сил.
Из кинематики известно, что
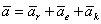
где 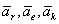 - соответственно относительное, переносное и кориолисово ускорения точки - соответственно относительное, переносное и кориолисово ускорения точки 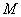 . .
Подставляя это значение 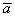 в равенство (1) получим в равенство (1) получим
|
| 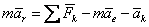
| (2)
| Введем два вектора 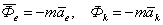 , численно равные , численно равные 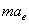 и и 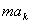 и направленные противоположно ускорениям и направленные противоположно ускорениям 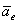 и и 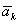 . Эти векторы назовем переносной и кориолисовой силами инерции. . Эти векторы назовем переносной и кориолисовой силами инерции.
Подставим эти векторы в уравнение (2)
|
| 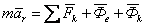
| (3)
| Уравнение (3) представляет собой основное уравнение динамики относительного движения материальной точки. Сопоставив (1) и (3) заключаем: в случае непоступательного переносного движения относительное движение материальной точки можно рассматривать как абсолютное, если к действующим на точку силам присоединить переносную и кориолисову силы инерции.
Это сопоставление показывает также, что в инерциальной системе отсчета ускорение точки является лишь результатом действия на нее сил, в то время как в неинерциальной системе ускорение является как результатом действия на нее сил, так и результатом движения самой системы отсчета.
Спроектировав (3) на оси подвижной системы отсчета 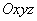 , получим дифференциальные уравнения относительного движения материальной точки , получим дифференциальные уравнения относительного движения материальной точки
|
В предыдущем параграфе показано было как определяется движение точки относительно неподвижной системы отсчета, абсолютное движение. Нередко приходится исследовать движение материальной точки относительно системы, которая сама движется и довольно сложным образом.
Точка М (рис.10) под действием некоторых сил 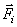 совершает сложное движение. Абсолютное определяется координатами x, y, z, относительное – координатами x 1, y 1, z 1.
совершает сложное движение. Абсолютное определяется координатами x, y, z, относительное – координатами x 1, y 1, z 1.
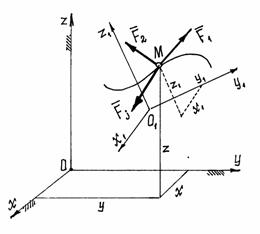
Рис.10
Составим основное уравнение динамики для точки  , где абсолютное ускорение
, где абсолютное ускорение  . Поэтому уравнение будет таким
. Поэтому уравнение будет таким  или
или 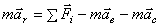 .
.
Но  - переносная сила инерции,
- переносная сила инерции,  - кориолисова сила инерции. Поэтому основное уравнение динамики для относительного движения запишем так
- кориолисова сила инерции. Поэтому основное уравнение динамики для относительного движения запишем так
 . (7)
. (7)
Спроектировав это векторное равенство на подвижные оси x 1, y 1, z 1, имея в виду, что проекции вектора ускорения на оси – есть вторые производные от соответствующих координат по времени, получим дифференциальные уравнения относительного движения
 (8)
(8)
Сравнивая эти уравнения с дифференциальными уравнениями абсолютного движения, замечаем, что относительное движение материальной точки определяется такими же методами, что и абсолютное, надо лишь кроме обычных сил учесть переносную силу инерции и кориолисову силу инерции.
Если переносное движение поступательное, равномерное и прямолинейное, т.е. подвижная система инерциальная, то ускорение  и
и 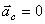 . Значит
. Значит 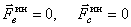 и дифференциальное уравнение (8) будет точно совпадать с дифференциальным уравнением абсолютного движения. Следовательно, движение точки во всех инерциальных системах описывается аналогичными законами (отличаются только постоянными интегрирования, зависящими от начальных условий).
и дифференциальное уравнение (8) будет точно совпадать с дифференциальным уравнением абсолютного движения. Следовательно, движение точки во всех инерциальных системах описывается аналогичными законами (отличаются только постоянными интегрирования, зависящими от начальных условий).
Поэтому невозможно установить, наблюдая за движением точки, движется система поступательно, равномерно и прямолинейно или находится в покое. Этот вывод впервые был сделан Г.Галилеем и называется его именем – принцип относительности Галилея.
Теорема Кориолиса[править | править исходный текст]
Пусть точка совершает сложное движение: движется относительно неинерциальной системы отсчёта  со скоростью
со скоростью  ; система
; система  при этом сама движется относительно инерциальной системы координат
при этом сама движется относительно инерциальной системы координат  , причём линейная скорость движущегося вместе с ней полюса
, причём линейная скорость движущегося вместе с ней полюса  равна
равна  , а угловая скорость системы
, а угловая скорость системы  равна
равна  .
.
Тогда абсолютная скорость рассматриваемой точки (то есть её линейная скорость в инерциальной системе координат) будет такой:
 , причём
, причём  ,
,
где  — радиус-вектор точки относительно полюса
— радиус-вектор точки относительно полюса  . Первые два слагаемых в правой части равенства представляют собой переносную скорость точки, а последнее — её относительную скорость.
. Первые два слагаемых в правой части равенства представляют собой переносную скорость точки, а последнее — её относительную скорость.
Продифференцируем это равенство по времени:

Найдём значение каждого слагаемого в инерциальной системе координат:



где  — линейное ускорение точки относительно системы
— линейное ускорение точки относительно системы  ,
,  — угловое ускорение системы
— угловое ускорение системы  .
.
Таким образом, имеем:

Полученное равенство служит математическим выражением теоремы Кориолиса: Абсолютное ускорение точки в сложном движении равно геометрической сумме её переносного ускорения (сумма первых трёх слагаемых в правой части), относительного ускорения (четвёртое слагаемое) и добавочного кориолисова ускорения (последнее слагаемое), равного  .
.
Используя обозначения  и
и  , получим запись теоремы Кориолиса в более сжатом виде:
, получим запись теоремы Кориолиса в более сжатом виде:

Причиной возникновения кориолисова ускорения является взаимное влияние друг на друга переносного и относительного движений.
Сам Кориолис выражал в 1835 г. свои результаты в иной форме, вводя в рассмотрение переносную и кориолисову силы инерции; общепринятая же ныне чисто кинематическая формулировка теоремы Кориолиса предложена в 1862 г. Анри Эме Резалем[7].
Заметим, что если система  также является неинерциальной и движется относительно другой системы, а та другая относительно следующей и т. д., то величины
также является неинерциальной и движется относительно другой системы, а та другая относительно следующей и т. д., то величины  ,
,  для системы
для системы  в последнем уравнении следует считать полными — то есть как сумму собственных ускорений (скоростей) всех систем координат (каждой относительно предыдущей), начиная с первой подвижной системы, а
в последнем уравнении следует считать полными — то есть как сумму собственных ускорений (скоростей) всех систем координат (каждой относительно предыдущей), начиная с первой подвижной системы, а  — абсолютным ускорением поступательного движения
— абсолютным ускорением поступательного движения  относительно неподвижной инерциальной системы координат.
относительно неподвижной инерциальной системы координат.
Заметим также, что в частности, чтобы точка относительно неинерциальной системы отсчёта двигалась прямолинейно по радиусу к оси вращения (см. рис.), необходимо приложить к ней силу, которая будет противодействующей суммы Кориолисовой силы 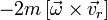 , переносной вращательной силы
, переносной вращательной силы 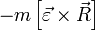 и переносной силы инерции поступательного движения системы отсчёта
и переносной силы инерции поступательного движения системы отсчёта 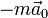 . Составляющая же ускорения
. Составляющая же ускорения  не отклонит тело от этой прямой, так как является осестремительным переносным ускорением и всегда направлена по этой прямой. Действительно, если рассматривать уравнение такого движения, то после компенсации в нём вышеупомянутых сил получится уравнение
не отклонит тело от этой прямой, так как является осестремительным переносным ускорением и всегда направлена по этой прямой. Действительно, если рассматривать уравнение такого движения, то после компенсации в нём вышеупомянутых сил получится уравнение  , которое если умножить векторно на
, которое если умножить векторно на  , то с учетом
, то с учетом  получим относительно
получим относительно  дифференциальное уравнение
дифференциальное уравнение  , имеющее при любых
, имеющее при любых  и
и  общим решением
общим решением  , которое и является уравнением такой прямой —
, которое и является уравнением такой прямой —  .
.



38. Механическая система. Масса системы. Центр масс системы и его координаты. Дифференциальные уравнения движения механической системы. Теорема о движении центра масс системы.







39. Классификация сил, действующих на механическую систему: силы внешние и внутренние. 

40 Моменты инерции твердого тела относительно оси и полюса. Радиус инерции. Теорема о моментах инерции относительно параллельных осей. Осевые моменты инерции некоторых однородных тел.

Момент инерции фигуры относительно координатной оси может быть представлен в виде произведения площади фигуры на квадрат радиуса инерции:

Ввели в рассмотрение еще две геометрические характеристики: радиусы инерции поперечного сечения относительно осей x и y, соответственно. Формула радиуса инерции имеет вид:

Главным центральным осям инерции соответствуют главные радиусы инерции:

Для прямоугольника (см. рис. 4.4, а) главные радиусы инерции равны:

Для круглого сечения формула главных радиусов инерции имеет вид:









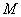 , движущуюся под действием приложенных к ней сил
, движущуюся под действием приложенных к ней сил 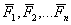 , являющихся результатом взаимодействия точки с другими телами. Будем изучать движение этой точки по отношению к осям
, являющихся результатом взаимодействия точки с другими телами. Будем изучать движение этой точки по отношению к осям 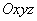 , которые в свою очередь каким-то известным нам образом движутся относительно инерциальной системы отсчета (неподвижных осей)
, которые в свою очередь каким-то известным нам образом движутся относительно инерциальной системы отсчета (неподвижных осей) 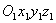 (рис.1).
(рис.1).
 Движение точки
Движение точки 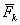 известны, основное уравнение динамики для абсолютного движения точки
известны, основное уравнение динамики для абсолютного движения точки 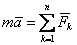
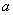 - абсолютное ускорение точки
- абсолютное ускорение точки 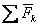 - геометрическая сумма приложенных к точке сил.
- геометрическая сумма приложенных к точке сил.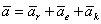
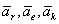 - соответственно относительное, переносное и кориолисово ускорения точки
- соответственно относительное, переносное и кориолисово ускорения точки 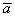 в равенство (1) получим
в равенство (1) получим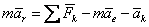
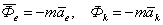 , численно равные
, численно равные 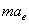 и
и 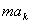 и направленные противоположно ускорениям
и направленные противоположно ускорениям 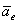 и
и 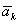 . Эти векторы назовем переносной и кориолисовой силами инерции.
. Эти векторы назовем переносной и кориолисовой силами инерции.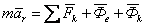
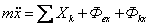 ,
,
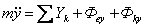 ,
,
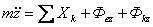
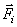 совершает сложное движение. Абсолютное определяется координатами x, y, z, относительное – координатами x 1, y 1, z 1.
совершает сложное движение. Абсолютное определяется координатами x, y, z, относительное – координатами x 1, y 1, z 1.
 , где абсолютное ускорение
, где абсолютное ускорение  . Поэтому уравнение будет таким
. Поэтому уравнение будет таким  или
или 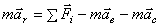 .
. - переносная сила инерции,
- переносная сила инерции,  - кориолисова сила инерции. Поэтому основное уравнение динамики для относительного движения запишем так
- кориолисова сила инерции. Поэтому основное уравнение динамики для относительного движения запишем так . (7)
. (7) (8)
(8) и
и 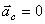 . Значит
. Значит 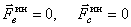 и дифференциальное уравнение (8) будет точно совпадать с дифференциальным уравнением абсолютного движения. Следовательно, движение точки во всех инерциальных системах описывается аналогичными законами (отличаются только постоянными интегрирования, зависящими от начальных условий).
и дифференциальное уравнение (8) будет точно совпадать с дифференциальным уравнением абсолютного движения. Следовательно, движение точки во всех инерциальных системах описывается аналогичными законами (отличаются только постоянными интегрирования, зависящими от начальных условий). со скоростью
со скоростью  ; система
; система  , причём линейная скорость движущегося вместе с ней полюса
, причём линейная скорость движущегося вместе с ней полюса  равна
равна  , а угловая скорость системы
, а угловая скорость системы  .
. , причём
, причём  ,
, — радиус-вектор точки относительно полюса
— радиус-вектор точки относительно полюса 



 — линейное ускорение точки относительно системы
— линейное ускорение точки относительно системы  — угловое ускорение системы
— угловое ускорение системы 
 .
. и
и  , получим запись теоремы Кориолиса в более сжатом виде:
, получим запись теоремы Кориолиса в более сжатом виде:
 ,
,  для системы
для системы  — абсолютным ускорением поступательного движения
— абсолютным ускорением поступательного движения 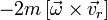 , переносной вращательной силы
, переносной вращательной силы 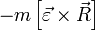 и переносной силы инерции поступательного движения системы отсчёта
и переносной силы инерции поступательного движения системы отсчёта 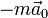 . Составляющая же ускорения
. Составляющая же ускорения  не отклонит тело от этой прямой, так как является осестремительным переносным ускорением и всегда направлена по этой прямой. Действительно, если рассматривать уравнение такого движения, то после компенсации в нём вышеупомянутых сил получится уравнение
не отклонит тело от этой прямой, так как является осестремительным переносным ускорением и всегда направлена по этой прямой. Действительно, если рассматривать уравнение такого движения, то после компенсации в нём вышеупомянутых сил получится уравнение  , которое если умножить векторно на
, которое если умножить векторно на  получим относительно
получим относительно  , имеющее при любых
, имеющее при любых  , которое и является уравнением такой прямой —
, которое и является уравнением такой прямой —  .
.

























