Пусть прямая пересекает Ох и Оусоотв-но в точках А и В. Применяем ф-луур-ния прямой по двум точкам. Координаты А(а;0) и В(0;в): 
Получаем ур-ние 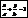 - ур-ниепрямой на отрезках координат.
- ур-ниепрямой на отрезках координат.
Угол между прямыми на плоскости.
Рассмотрим 2 прямые  ,
,  и
и 
О.Углом между прямыми  и
и  наз-тсяменьший из смежных углов, образованных этими пересекающимися прямыми. Очевидно, что jÎ[0;p]. Не сложно заметить, что
наз-тсяменьший из смежных углов, образованных этими пересекающимися прямыми. Очевидно, что jÎ[0;p]. Не сложно заметить, что  . Тогда
. Тогда 
 , по
, по  -это
-это  ,
,  -это
-это  Þ
Þ  . Если прямые параллельны, тогда Ðj=0,
. Если прямые параллельны, тогда Ðj=0, 
 . След-но
. След-но  =
=  - условие параллельности прямых. Если прямые ^, то
- условие параллельности прямых. Если прямые ^, то 
 ,
,  , след-но
, след-но  , т.е.
, т.е.  - условие перпендикулярности прямых.
- условие перпендикулярности прямых.
Пр. Найти угол между прямыми  и
и 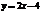

т.к. мы выбираем наим. из смежных углов, то  и ф-ла примет вид
и ф-ла примет вид 
5))Расстояние от точки до прямой на плоскости и взаимное расположение прямых на плоскости.
1) Расстояние от точки до прямой на плоскости.
Т. Расст.  от данной точки
от данной точки 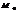 до данной прямой
до данной прямой  , заданной ур-нием
, заданной ур-нием  на плоскости задается ф-лой
на плоскости задается ф-лой

Док-во:
пусть в прямоуг.системе координат Ур-ние прямой имеет вид: 
Не сложно заметить,что расстояние от точки до этой прямой = 2 площади треугольника,разденить на его основание,а также площадь 
А основание треугольника:= 
Запишем Ур-ние прямой проходящей через 2 точки:

Приводим к линейному виду
х( )+у(
)+у( )-х1(
)-х1( )+у1(
)+у1(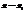 )
)
т.к. по предположению а=m( );b=m(x1-x2);с=m(у1(
);b=m(x1-x2);с=m(у1( )-х1(
)-х1( ))
))
d= (х( )+у(
)+у( )-х1(
)-х1( )+у1(
)+у1( ))/
))/ 
=/ (-а/m)*х-(b/m)*y-c/m / / корень из (-b/m)^2 +(a/m)^2
1/m выносим и сокращаем,получаем исходную формулу.
Пр. Найти расстояние от М(4,3) до прямой 

2) Взаимное расположение двух прямых на плоскости.
Пусть прямые  и
и  заданы своими общими ур-ниями
заданы своими общими ур-ниями 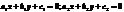
Рассм. с-му, состоящих из этих ур-ний с неизвестными  и
и  .
.
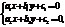

1 случай:  ,
,  ур-ние имеет бесконечное множ-во решений. (прямые совпадают)
ур-ние имеет бесконечное множ-во решений. (прямые совпадают)  и
и 
2 случай:  ,
,  , т.е.
, т.е. 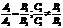 - ур-ние решений не имеет, т.к. прямые параллельны.
- ур-ние решений не имеет, т.к. прямые параллельны.
3 случай:  , ур-ние имеет единственное решение, т.е. прямые пересекаются в единственной точке.
, ур-ние имеет единственное решение, т.е. прямые пересекаются в единственной точке.
Матрицы и действия над ними.
Таблица чисел вида 
 , состоящая из nстрок и mстолбцов наз-тся матрицей размерности n´m.
, состоящая из nстрок и mстолбцов наз-тся матрицей размерности n´m.
Числа 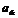 наз-ют её элементами, если m¹n, то матрицу наз-ют прямоугольной, если n=m, то квадратной. Если n=1, а m>1, то матрица примет вид
наз-ют её элементами, если m¹n, то матрицу наз-ют прямоугольной, если n=m, то квадратной. Если n=1, а m>1, то матрица примет вид  и наз-тся матрицей-строкой. Если же n>1, а m=1, то матрица наз-тся матрицей-столбцом. Число строк в квадратной матрице наз-ют ее порядком. Две матрицы наз-ют равными если они имеют одинак. размерность и соответствующие элементы равны.
и наз-тся матрицей-строкой. Если же n>1, а m=1, то матрица наз-тся матрицей-столбцом. Число строк в квадратной матрице наз-ют ее порядком. Две матрицы наз-ют равными если они имеют одинак. размерность и соответствующие элементы равны.
Сложение и вычитание матриц.
О.Суммой двух матриц А и Водинакового размера n´mназ-тся матрица С размерности n´m, элементы к-рой равны сумме соотв-щих элементов матриц А и В.
О. Матрица 0 размерности m´n, все элементы к-рой=0 наз-тся нулевой матрицей.
О.Разностью двух матриц А и В размерности m´nназ-тся матрица С размерности m´n такая, что А=В+С. Из определения следует, что элементы матрицы С равны разности соотв. элементов матриц А и В.
Св-ва сложения:
ü сложение матриц коммутативно, т.е. А+В=В+А
ü сложение матриц ассоциативно, т.е. (А+В)+С=А+(В+С)
ü А+0=0+А=А
Умножение матриц на число.
О. Произведение матрицы А на число aназ-тся матрицей aА, элементы к-рой равны произведению числа a на соотв. элемент матрицы А.
Умножение матриц.
О. Произведение матриц размерности m´n и матрицы В размерности 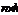 наз-тся матрица С размерности
наз-тся матрица С размерности  , элементы к-рой
, элементы к-рой 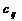 вычисляются как сумма произведений соотв-щих элементов
вычисляются как сумма произведений соотв-щих элементов 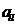
 -строки матрицы А на
-строки матрицы А на 
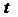 -столбца матрицы В.
-столбца матрицы В.
Пр. 
О.Квадратная матрица порядка nназ-тсяединичной. Обозначается  это матрица с единицами на главной диагонали.
это матрица с единицами на главной диагонали.
Св-ва умножения:
ü умножение не коммутативно, т.е. А*В¹В*А
ü умножение матриц ассоциативно, т.е. (А*В)*С=А*(В*С), если такие произведения существуют.
ü если А матрицы размерности m´n, В размерности  , то
, то 
Транспонирование матрицы.
О. Если в матрице А размерности n´m все стороки заменить соотв-щими столбцами, то получим матрицу  размерности m´n, к-руюназ-ют транспонированной матрицей А.
размерности m´n, к-руюназ-ют транспонированной матрицей А.
Св-ва транспонирования:
Y 
Y 
Y 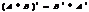
Элементарные преобразования строк матрицы:
* умножение строк матрицы на ненулевое действительное число;
* прибавление к одной строке матрицы другой, умноженной на нек-рое число.
Лемма: с помощью элементарных преобразований можно поменять местами две любые строки матрицы.
Ступенчатая матрица -матрица, обладающая след.св-вами:
1. если iтая строка нулевая то  также нулевая.
также нулевая.
2. если первые ненулевые элементы  той строки и
той строки и  находятся соотв-но в столбцах с номерами k и p. Тогда k<p
находятся соотв-но в столбцах с номерами k и p. Тогда k<p
Теорема. Любую матрицу можно привести к ступенчатому виду с помощью элементарных преобразований строк матрицы.
О. Ранг матрицы - число ненулевых строк в ступенчатом виде этой матрицы.
Пр. 
- ранг 3
Определители, их свойства.
О. Определителем 2-го порядка наз-тся число, вычисляемое по ф-ле 

Определителем 3-го порядка соответствующих матрицы А называется число вычисляемое по формуле, которую удобно связывать со следующим правилом:
Т. Определитель 3-го порядка равен произведению элементов какой-либо строки(столбца) на соотв-щее алгебраическое дополнение.

Определителем  -го порядка, соотв-щим квадратной матрице
-го порядка, соотв-щим квадратной матрице  -го порядка, наз-тся число, равное сумме произведений элементов какой-либо строки(столбца) на их алгебраическое дополнение.
-го порядка, наз-тся число, равное сумме произведений элементов какой-либо строки(столбца) на их алгебраическое дополнение.
О. Минором  наз-ют определитель, полученный из данного путем вычеркивания
наз-ют определитель, полученный из данного путем вычеркивания  той строки и
той строки и  –того столбца. Алгебраическимдаполнением
–того столбца. Алгебраическимдаполнением  наз-ют число равное
наз-ют число равное 
Св-ва определителя:
f Определитель треугольной матрицы равен произведению элементов главной диагонали
f Опред. матрицы с нулевой строкой или нулевым столбцом равен нулю
f При транспонировании матрицы, определитель не меняется.
f Если матрица А получается из матрицы В умножением каждого элемента нек-рой строки(столбца) на число  , то определитель равен
, то определитель равен 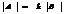
f Если матрица В получается из матрицы А перестановкой строк(столбцов), то определитель меняет знак.
f Определитель матрицы с пропорциональными строками(столбцами) равен 0.
f Определитель матрицы не меняется если к одной из строк прибавить другую, умноженную на нек-рое действительное число.
f Определитель произведения равен произведению определителей.
 , где А и В- квадратные матрицы одног7о порядка.
, где А и В- квадратные матрицы одног7о порядка.
Обратная матрица.
Квадратная матрица А порядка  наз-тся обратимой, если сущ-ет такая матрица В, что
наз-тся обратимой, если сущ-ет такая матрица В, что  . В этом случае В-обратная для матрицы А и обозначают А-1.
. В этом случае В-обратная для матрицы А и обозначают А-1.
Т. Справедливы след.утверждения:
² если матрица обратима, то сущ-ет только одна ей обратная матрица.
² определитель обратимой матрицы отличен от 0.
² если А и В- обратимые матрицы порядка  , то АВ- также обратима. Причем обратная для произведения равна В-1А-1. (АВ)-1= В-1А-1
, то АВ- также обратима. Причем обратная для произведения равна В-1А-1. (АВ)-1= В-1А-1
Док-во:
1)пусть В и С матрицы обратные матрице А тогда АВ=ВА=Е и АС=СА=Е,тогда В=В*Е=АС*В=ЕС=С,противоречиепоказывающее,что обратная матрица только одна.
2)т.к.А*А-1=Е,то /А*А-1/=/Е/=1, А-1 не=0;
3) (АВ)-1= В-1А-1докажем,что В-1А-1 обратная для (АВ),
(АВ)* В-1А-1=А*Е*А-1=Е
(АВ)-1= В-1А-1=Е
Т. Квадратная матрица А обратима тогда и только тогда, когда ее определитель отличен от 0. Если 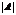 отличен от 0, то А-1=
отличен от 0, то А-1= 

Пр. 
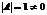 ,
,  ;
; 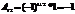 ;
;  ;
; 


Понятие непрерывности ф-и.
Ф.  , определенная на
, определенная на 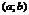 наз-тся непрерывной в точке
наз-тся непрерывной в точке  если
если 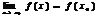
Т. Ф.  непрерывна в точке
непрерывна в точке  только тогда, когда
только тогда, когда 
Док-во:
Предел при (х-х0) стремящемся к 0(f(x)-f(x0))=0;предел при х стремящемся к х0f(x)=f(x0)
Т. Если ф.  и
и  непрерывны в точке
непрерывны в точке  , то непрерывна в этой точке их сумма, разность, произведение, а также частное при усл.
, то непрерывна в этой точке их сумма, разность, произведение, а также частное при усл. 
Док-во:
Док-во непосредственно следует из определения непрерывности и свойств
О. Ф. наз-тся непрерывной на интервале, если она непрерывна в каждой точке этого интервала.
1-ая теорема Бальцама - Коши: Пусть ф.  непрерывна на отрезке
непрерывна на отрезке  и на концах отрезка имеет значение разных знаков, тогда сущ-ет точка
и на концах отрезка имеет значение разных знаков, тогда сущ-ет точка  такая, что
такая, что 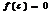
Т. Пусть ф.  непрерывна на отрезке
непрерывна на отрезке  причем
причем  . Пусть
. Пусть  –число, заключенное между А и В, тогда сущ-ет точка
–число, заключенное между А и В, тогда сущ-ет точка 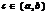 такая, что
такая, что 
1-ая теорема Вейерштрасса: Если ф.  определена и непрерывна на
определена и непрерывна на  , то она ограничена на этом отрезке.
, то она ограничена на этом отрезке.
2-ая теорема Вейерштрасса: Если  непрерывна на
непрерывна на  , то она достигает на этом отрезке своего наиб.инаим. значения.
, то она достигает на этом отрезке своего наиб.инаим. значения.
Системы линейных уравнений.
Совокупность ур-ний вида
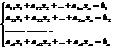 (1) - с-ма
(1) - с-ма  –линейных ур-ний с
–линейных ур-ний с  –неизвестным
–неизвестным 
Числа  наз-тся коэффициентами с-мы. Числа
наз-тся коэффициентами с-мы. Числа  - свободными коэффициентами.
- свободными коэффициентами.
Решением с-мы (1) наз-тся совокупность чисел  при подстановке к-рых в с-му (1) вместо
при подстановке к-рых в с-му (1) вместо  получаем верные числовые рав-ва.
получаем верные числовые рав-ва.
Решить с-му, значит найти все ее решения, либо доказать, что их нет.С-маназ-тся совместной, если она имеет хотя бы одно решение, несовместной- если решений нет. Матрица составлена из коэф-тов
 наз-тся матрицей с-мы (1).
наз-тся матрицей с-мы (1).
Если к данной матрице добавить столбец свободных коэф-тов, такую матрицу наз-ют расширенной матрицей с-мы

Критерий совместимости с-мы.
Т. Кронекера-Копелли: Для того, чтобы с-ма линейных ур-нийбыла совместно необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом матрицы с-мы.
Пр. 

Метод Гаусса: применяется для произвольной с-мы линейных ур-ний.
О. С-му будем наз-тьступенчатой, если матрица имеет ступенчатый вид. При решении с-м линейныхур-ний нам понадобится след алгоритм:
1. Запишем расшир. матрицу и приведем ее к ступенчатому виду.
2. если ранги не равны, то с-манесовместна
3. если ранги равны и равны числу 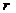 , то с-масовместна и остается записать ее решение
, то с-масовместна и остается записать ее решение
4. используя ступенчатый вид расширенной матрицы запишем соотв. ступенчатую с-му.
5. если 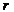 =
=  , т.е. ранг совпадает с числом неизвестных, то с-ма имеет единственное решение.
, т.е. ранг совпадает с числом неизвестных, то с-ма имеет единственное решение.
 Двигаясь снизу вверх выражаем каждую из неизвестных.
Двигаясь снизу вверх выражаем каждую из неизвестных.
6. если  <
<  , то в с-ме
, то в с-ме 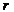 ур-ний и
ур-ний и  неизвестных. Неизвестные, к-рые первыми встречаются в ступенчатой с-ме (
неизвестных. Неизвестные, к-рые первыми встречаются в ступенчатой с-ме ( -неизвестных) назовем главными неизвестными, а остальные –свободными неизвестными. Снизу вверх выражаем каждую из главных неизвестных свободные неизвестные могут принимать любые значения, в этом случае с-ма имеет бесконечно много решений.
-неизвестных) назовем главными неизвестными, а остальные –свободными неизвестными. Снизу вверх выражаем каждую из главных неизвестных свободные неизвестные могут принимать любые значения, в этом случае с-ма имеет бесконечно много решений.
Правила Крамера:
С-ма линейных ур-нийназ-тся крамеровской, если число ур-ний совпадает с числом неизвестных и определитель матрицы с-мы отличен от 0.
Т. Крамеровская с-ма имеет единственное решение, к-рое находится по ф-лам
 , где D-определитель матрицы с-мы, а
, где D-определитель матрицы с-мы, а  - определитель, полученный из D подстановкой вместо
- определитель, полученный из D подстановкой вместо  того столбца столбец свободных коэф-тов.
того столбца столбец свободных коэф-тов.
Док-во:
т.к матрица системы А не вырождена,то для нее существует обратная матрица А-1,вычисляемая по формуле:
А-1= 

Запишем систему в виде матричного Ур-ния АХ=С,
А-1АХ= А-1С
ЕХ= А-1С;Х= А-1С
Предположим,что решение не единственное,тогда
АХ1=С и АХ2=С;АХ1=АХ2;Х1=Х2-данное протеворечиепоказывает,что решение единственное..найдемрешение Ур-ния Х= А-1С
Пр. 
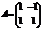 ;
;  ;
;  ;
;  ;
; 




 - ур-ниепрямой на отрезках координат.
- ур-ниепрямой на отрезках координат. ,
,  и
и 
 и
и  наз-тсяменьший из смежных углов, образованных этими пересекающимися прямыми. Очевидно, что jÎ[0;p]. Не сложно заметить, что
наз-тсяменьший из смежных углов, образованных этими пересекающимися прямыми. Очевидно, что jÎ[0;p]. Не сложно заметить, что  . Тогда
. Тогда 
 , по
, по  -это
-это  ,
,  -это
-это  Þ
Þ  . Если прямые параллельны, тогда Ðj=0,
. Если прямые параллельны, тогда Ðj=0,  . След-но
. След-но  =
=  - условие параллельности прямых. Если прямые ^, то
- условие параллельности прямых. Если прямые ^, то  ,
,  , след-но
, след-но  , т.е.
, т.е.  - условие перпендикулярности прямых.
- условие перпендикулярности прямых. и
и 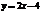

 и ф-ла примет вид
и ф-ла примет вид 
 от данной точки
от данной точки 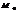 до данной прямой
до данной прямой  , заданной ур-нием
, заданной ур-нием  на плоскости задается ф-лой
на плоскости задается ф-лой




 )+у(
)+у( )-х1(
)-х1( )+у1(
)+у1(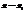 )
) );b=m(x1-x2);с=m(у1(
);b=m(x1-x2);с=m(у1( )-х1(
)-х1( ))
)) )+у(
)+у( )-х1(
)-х1( ))/
))/ 


 и
и  заданы своими общими ур-ниями
заданы своими общими ур-ниями 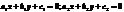
 и
и  .
.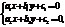

 ,
,  ур-ние имеет бесконечное множ-во решений. (прямые совпадают)
ур-ние имеет бесконечное множ-во решений. (прямые совпадают)  и
и 
 ,
,  , т.е.
, т.е. 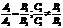 - ур-ние решений не имеет, т.к. прямые параллельны.
- ур-ние решений не имеет, т.к. прямые параллельны. , ур-ние имеет единственное решение, т.е. прямые пересекаются в единственной точке.
, ур-ние имеет единственное решение, т.е. прямые пересекаются в единственной точке.
 , состоящая из nстрок и mстолбцов наз-тся матрицей размерности n´m.
, состоящая из nстрок и mстолбцов наз-тся матрицей размерности n´m.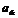 наз-ют её элементами, если m¹n, то матрицу наз-ют прямоугольной, если n=m, то квадратной. Если n=1, а m>1, то матрица примет вид
наз-ют её элементами, если m¹n, то матрицу наз-ют прямоугольной, если n=m, то квадратной. Если n=1, а m>1, то матрица примет вид  и наз-тся матрицей-строкой. Если же n>1, а m=1, то матрица наз-тся матрицей-столбцом. Число строк в квадратной матрице наз-ют ее порядком. Две матрицы наз-ют равными если они имеют одинак. размерность и соответствующие элементы равны.
и наз-тся матрицей-строкой. Если же n>1, а m=1, то матрица наз-тся матрицей-столбцом. Число строк в квадратной матрице наз-ют ее порядком. Две матрицы наз-ют равными если они имеют одинак. размерность и соответствующие элементы равны.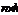 наз-тся матрица С размерности
наз-тся матрица С размерности  , элементы к-рой
, элементы к-рой 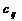 вычисляются как сумма произведений соотв-щих элементов
вычисляются как сумма произведений соотв-щих элементов 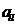
 -строки матрицы А на
-строки матрицы А на 
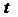 -столбца матрицы В.
-столбца матрицы В.
 это матрица с единицами на главной диагонали.
это матрица с единицами на главной диагонали. , то
, то 
 размерности m´n, к-руюназ-ют транспонированной матрицей А.
размерности m´n, к-руюназ-ют транспонированной матрицей А.

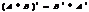
 также нулевая.
также нулевая. той строки и
той строки и  находятся соотв-но в столбцах с номерами k и p. Тогда k<p
находятся соотв-но в столбцах с номерами k и p. Тогда k<p



 -го порядка, соотв-щим квадратной матрице
-го порядка, соотв-щим квадратной матрице  -го порядка, наз-тся число, равное сумме произведений элементов какой-либо строки(столбца) на их алгебраическое дополнение.
-го порядка, наз-тся число, равное сумме произведений элементов какой-либо строки(столбца) на их алгебраическое дополнение. наз-ют определитель, полученный из данного путем вычеркивания
наз-ют определитель, полученный из данного путем вычеркивания  той строки и
той строки и  –того столбца. Алгебраическимдаполнением
–того столбца. Алгебраическимдаполнением  наз-ют число равное
наз-ют число равное 
 , то определитель равен
, то определитель равен 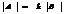
 , где А и В- квадратные матрицы одног7о порядка.
, где А и В- квадратные матрицы одног7о порядка. наз-тся обратимой, если сущ-ет такая матрица В, что
наз-тся обратимой, если сущ-ет такая матрица В, что  . В этом случае В-обратная для матрицы А и обозначают А-1.
. В этом случае В-обратная для матрицы А и обозначают А-1. , то АВ- также обратима. Причем обратная для произведения равна В-1А-1. (АВ)-1= В-1А-1
, то АВ- также обратима. Причем обратная для произведения равна В-1А-1. (АВ)-1= В-1А-1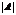 отличен от 0, то А-1=
отличен от 0, то А-1= 


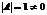 ,
,  ;
; 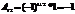 ;
;  ;
; 


 , определенная на
, определенная на 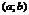 наз-тся непрерывной в точке
наз-тся непрерывной в точке  если
если 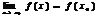
 непрерывна в точке
непрерывна в точке  только тогда, когда
только тогда, когда 
 и
и  непрерывны в точке
непрерывны в точке  , то непрерывна в этой точке их сумма, разность, произведение, а также частное при усл.
, то непрерывна в этой точке их сумма, разность, произведение, а также частное при усл. 
 непрерывна на отрезке
непрерывна на отрезке  и на концах отрезка имеет значение разных знаков, тогда сущ-ет точка
и на концах отрезка имеет значение разных знаков, тогда сущ-ет точка  такая, что
такая, что 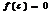
 непрерывна на отрезке
непрерывна на отрезке  причем
причем  . Пусть
. Пусть  –число, заключенное между А и В, тогда сущ-ет точка
–число, заключенное между А и В, тогда сущ-ет точка 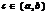 такая, что
такая, что 
 определена и непрерывна на
определена и непрерывна на  , то она ограничена на этом отрезке.
, то она ограничена на этом отрезке. , то она достигает на этом отрезке своего наиб.инаим. значения.
, то она достигает на этом отрезке своего наиб.инаим. значения.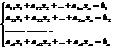 (1) - с-ма
(1) - с-ма  –линейных ур-ний с
–линейных ур-ний с  –неизвестным
–неизвестным 
 наз-тся коэффициентами с-мы. Числа
наз-тся коэффициентами с-мы. Числа  - свободными коэффициентами.
- свободными коэффициентами. при подстановке к-рых в с-му (1) вместо
при подстановке к-рых в с-му (1) вместо  получаем верные числовые рав-ва.
получаем верные числовые рав-ва. наз-тся матрицей с-мы (1).
наз-тся матрицей с-мы (1).


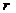 , то с-масовместна и остается записать ее решение
, то с-масовместна и остается записать ее решение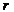 =
=  , т.е. ранг совпадает с числом неизвестных, то с-ма имеет единственное решение.
, т.е. ранг совпадает с числом неизвестных, то с-ма имеет единственное решение. Двигаясь снизу вверх выражаем каждую из неизвестных.
Двигаясь снизу вверх выражаем каждую из неизвестных. <
<  , где D-определитель матрицы с-мы, а
, где D-определитель матрицы с-мы, а  - определитель, полученный из D подстановкой вместо
- определитель, полученный из D подстановкой вместо 


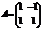 ;
;  ;
;  ;
;  ;
; 



