Функция f(x) называется непрерывной в точке 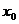 , если она удовлетворяет след.трем условиям: 1)определена в точке
, если она удовлетворяет след.трем условиям: 1)определена в точке 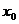 (т.е. существует f(
(т.е. существует f(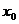 )); 2) имеет конечный предел функции при
)); 2) имеет конечный предел функции при 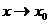 ;3) этот предел равен значению функции в точке
;3) этот предел равен значению функции в точке 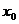 , т.е.
, т.е.
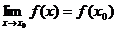
Функция y=f(x) называется непрерывной в точке 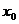 , если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:
, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: 
Св-ва функций, непрерывных на отрезке:
1) Если функция y=f(x) непрерывна на отрезке [a,b], то она ограничена на этом отрезке.
2) Если функция y=f(x) непрерывна на отрезке [a,b], то она достигает на этом отрезке наименьшего значения m и наибольшего значения М.
3) Если функция у=f(x) непрерывна на отрезке [a,b] и значения ее на концах отрезка f(a) и f(b) имеют противоположные знаки, то внутри отрезка найдется точка 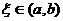 такая, что f(
такая, что f(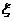 )=0/
)=0/
7. Производная функции и дифференциал.
Производной функции у=f(x) наз.предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю(если этот предел существует): 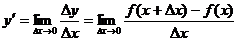 .
.
Нахождение производной функции наз. Дифференцированием этой функции. Если функция в точке х имеет конечную производную, то функция наз. Дифференцируемой в этой точке.
Если функция у=f(x) дифференцируема в точке 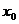 , то она в этой точке непрерывна. (непрерывность функции-необходимое, но недостаточное условие дифференцируемости функции.)
, то она в этой точке непрерывна. (непрерывность функции-необходимое, но недостаточное условие дифференцируемости функции.)
Дифференциалом функции наз.Главная, линейная относительно 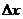 часть приращения функции, равная
часть приращения функции, равная 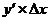 . Dy=dx=
. Dy=dx= 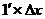
Dy= 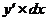 .
.
Дифференциал равен приращению ординаты касательной в данной точке, когда х получает приращение 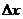 .
.
Св-ва дифференциала: 1)d(cf)=cdf, c=const. D(cf)= 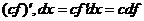
2)d(f 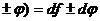
3)d(f 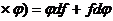
4)d(f/ 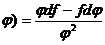 .
.
8. Производные и дифференциалы высших порядков.
Производной n-ого порядка наз.производная от производной (n-1)-ого порядка. Обозначение: 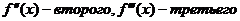 и т.п. Для обозначения производных более высокого порядка используются арабские цифры в скобках или римские цифры.
и т.п. Для обозначения производных более высокого порядка используются арабские цифры в скобках или римские цифры.
Дифф.Высш.порядков. 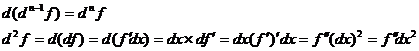
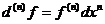

Геометрический и физический смысл производной и дифференциала. Приложения производной в экономических расчетах. (для экономики)
10. Правила дифференцирования сумм, произведения и частного функций. Производная сложной и обратной функций.
Если функции u=u(x) и v=v(x) имеют в точке x производные, то сумма (разность), произведение и частное этих функций также имеют производные в этой точке, и справедливы следующие формулы:
1) (u±v) =u/±v/,
2) (u·v)/=u/v+v/u,
3) 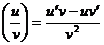
Теорема. Если функция y=f(x) имеет в точке 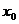 производную
производную 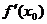 не равную нулю, то обратная функция x=φ(y) имеет в соответствующей точке
не равную нулю, то обратная функция x=φ(y) имеет в соответствующей точке 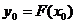 производную, которая вычисляется по формуле: φ/(y0)=1f/(x0).
производную, которая вычисляется по формуле: φ/(y0)=1f/(x0).
Доказательство y/=limΔx→0ΔxΔy,ϕ/(x0)=limΔy→0ΔyΔx=limΔy→01ΔxΔy=∣∣∣limΔx→0Δy=0∣∣∣=1limΔx→0ΔxΔy=1f/(x0).
Теорема Если функция x=φ(t) имеет производную в точке t0, а функция y=f(x) имеет производную в точкеx0=φ(t0), то сложная функция y(t)=f(φ(t)) имеет производную в точке t0 и справедлива формула: y/(t0)=f/(x0)·ϕ/(t0).



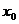 , если она удовлетворяет след.трем условиям: 1)определена в точке
, если она удовлетворяет след.трем условиям: 1)определена в точке 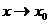 ;3) этот предел равен значению функции в точке
;3) этот предел равен значению функции в точке 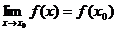

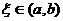 такая, что f(
такая, что f(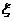 )=0/
)=0/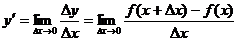 .
.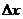 часть приращения функции, равная
часть приращения функции, равная 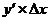 . Dy=dx=
. Dy=dx= 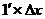
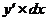 .
.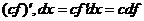
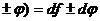
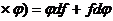
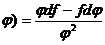 .
.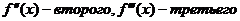 и т.п. Для обозначения производных более высокого порядка используются арабские цифры в скобках или римские цифры.
и т.п. Для обозначения производных более высокого порядка используются арабские цифры в скобках или римские цифры.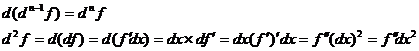
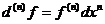

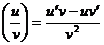
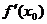 не равную нулю, то обратная функция x=φ(y) имеет в соответствующей точке
не равную нулю, то обратная функция x=φ(y) имеет в соответствующей точке 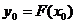 производную, которая вычисляется по формуле: φ/(y0)=1f/(x0).
производную, которая вычисляется по формуле: φ/(y0)=1f/(x0).


