Вычетом функции  относительно точки
относительно точки  (обозначается
(обозначается  или
или  ) называется число, равное
) называется число, равное
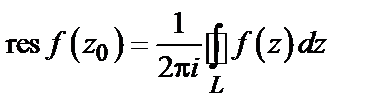 ,
,
где  - простой замкнутый контур, лежащий в области аналитичности функции
- простой замкнутый контур, лежащий в области аналитичности функции  и содержащий внутри себя только одну особую точку
и содержащий внутри себя только одну особую точку  .
.
В качестве  удобно брать окружность
удобно брать окружность  достаточно малого радиуса
достаточно малого радиуса  . Из определения следует, что вычет функции
. Из определения следует, что вычет функции  совпадает с коэффициентом
совпадает с коэффициентом  разложения ее в ряд Лорана по степеням
разложения ее в ряд Лорана по степеням  :
:  . Отсюда следует, что вычет в устранимой особой точке равен нулю. Вычет
. Отсюда следует, что вычет в устранимой особой точке равен нулю. Вычет  в простом полюсе равен
в простом полюсе равен
 .
.
Вычет функции  в полюсе
в полюсе  порядка
порядка  равен
равен
 .
.
Если  – существенно особая точка функции
– существенно особая точка функции  , то для определения
, то для определения  необходимо найти коэффициент
необходимо найти коэффициент  в лорановском разложении функции
в лорановском разложении функции  в окрестности точки
в окрестности точки  .
.
Теорема Коши о вычетах. Если функция  - аналитическая на границе
- аналитическая на границе  области
области  и внутри области, за исключением конечного числа изолированных особых точек
и внутри области, за исключением конечного числа изолированных особых точек  , то
, то



Теоремы Коши для односвязной и для многосвязной областей.
Теорема Коши для односвязной области. Если D - односвязная ограниченная область, w = f(z) - аналитическая в этой области функция, то для любого кусочно-гладкого замкнутого контура L, лежащего в D, интеграл от f(z) по L равен нулю:. 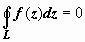 Доказательство. Удивительно, но эта важнейшая теорема непосредственно и просто следует из условий Коши-Римана и формулы Грина. Так как, по доказанному выше,
Доказательство. Удивительно, но эта важнейшая теорема непосредственно и просто следует из условий Коши-Римана и формулы Грина. Так как, по доказанному выше, 
 , то, применяя к действительным криволинейным интегралам формулу Грина, получим
, то, применяя к действительным криволинейным интегралам формулу Грина, получим  вследствие условий Коши-Римана.
вследствие условий Коши-Римана.  Символом G в доказательстве обозначена область, заключённая внутри контура L.
Символом G в доказательстве обозначена область, заключённая внутри контура L.
2. Теорема Коши для многосвязной области. Если функция w = f(z) аналитична в замкнутой многосвязной ограниченной области  , ограниченной контурами L0 (внешняя граница), L1, L2, …, Lk, то интеграл от f(z), взятый по полной границе области
, ограниченной контурами L0 (внешняя граница), L1, L2, …, Lk, то интеграл от f(z), взятый по полной границе области  , проходимой так, что область остаётся с одной стороны, равен нулю.
, проходимой так, что область остаётся с одной стороны, равен нулю.
Интегральные формулы Коши для ФКП:прямая и обобщенная.
Если функция  аналитическая в
аналитическая в  ,
,  и
и  - контур, охватывающий точку
- контур, охватывающий точку  , то
, то
 ,
,  . (10)
. (10)
Формула(10) показывает, что значения аналитической ФКП внутри контура определяются значениями функций на самом контуре. Например, если ФКП f(z0) на (y) равна нулю (или, вообще, одному и тому же постоянному числу c), то, как следует из (10), f(z)=0 (илиf(z)=c) во всех точках внутри контура(y). Действительнозначные дифференцируемые функции в действительной области подобным свойством не обладают. Например,  – определена и непрерывна внутри и на границе круга
– определена и непрерывна внутри и на границе круга  . На контуре
. На контуре  эта функция f(x,y) равна нулю, но в любой внутренней точке круга
эта функция f(x,y) равна нулю, но в любой внутренней точке круга  .
.
При этом функция  имеет всюду в
имеет всюду в  производные любого порядка, для которых справедливы формулы
производные любого порядка, для которых справедливы формулы
 .
.
Элементы теории поля
Скалярное поле
Определения
Скалярное поле определяется скалярной функцией точки  где
где  - точка пространства,
- точка пространства,  - ее радиус-вектор.
- ее радиус-вектор.
Градиент
Градиент скалярного поля – вектор

Свойства градиента

Векторное поле Определение Векторное поле определяется векторной функцией точки 
где  - точка пространства,
- точка пространства,  - ее радиус-вектор.
- ее радиус-вектор.
Формула Остроградского





 относительно точки
относительно точки  (обозначается
(обозначается  или
или  ) называется число, равное
) называется число, равное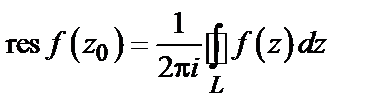 ,
, - простой замкнутый контур, лежащий в области аналитичности функции
- простой замкнутый контур, лежащий в области аналитичности функции  и содержащий внутри себя только одну особую точку
и содержащий внутри себя только одну особую точку  достаточно малого радиуса
достаточно малого радиуса  . Из определения следует, что вычет функции
. Из определения следует, что вычет функции  совпадает с коэффициентом
совпадает с коэффициентом  разложения ее в ряд Лорана по степеням
разложения ее в ряд Лорана по степеням  :
:  . Отсюда следует, что вычет в устранимой особой точке равен нулю. Вычет
. Отсюда следует, что вычет в устранимой особой точке равен нулю. Вычет  в простом полюсе равен
в простом полюсе равен .
. в полюсе
в полюсе  равен
равен .
. необходимо найти коэффициент
необходимо найти коэффициент  в лорановском разложении функции
в лорановском разложении функции  в окрестности точки
в окрестности точки  - аналитическая на границе
- аналитическая на границе  и внутри области, за исключением конечного числа изолированных особых точек
и внутри области, за исключением конечного числа изолированных особых точек  , то
, то


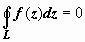 Доказательство. Удивительно, но эта важнейшая теорема непосредственно и просто следует из условий Коши-Римана и формулы Грина. Так как, по доказанному выше,
Доказательство. Удивительно, но эта важнейшая теорема непосредственно и просто следует из условий Коши-Римана и формулы Грина. Так как, по доказанному выше, 
 , то, применяя к действительным криволинейным интегралам формулу Грина, получим
, то, применяя к действительным криволинейным интегралам формулу Грина, получим  вследствие условий Коши-Римана.
вследствие условий Коши-Римана.  Символом G в доказательстве обозначена область, заключённая внутри контура L.
Символом G в доказательстве обозначена область, заключённая внутри контура L. , ограниченной контурами L0 (внешняя граница), L1, L2, …, Lk, то интеграл от f(z), взятый по полной границе области
, ограниченной контурами L0 (внешняя граница), L1, L2, …, Lk, то интеграл от f(z), взятый по полной границе области  аналитическая в
аналитическая в  и
и  - контур, охватывающий точку
- контур, охватывающий точку  ,
,  . (10)
. (10) – определена и непрерывна внутри и на границе круга
– определена и непрерывна внутри и на границе круга  . На контуре
. На контуре  эта функция f(x,y) равна нулю, но в любой внутренней точке круга
эта функция f(x,y) равна нулю, но в любой внутренней точке круга  .
. имеет всюду в
имеет всюду в  .
. где
где  - точка пространства,
- точка пространства,  - ее радиус-вектор.
- ее радиус-вектор.







