Билет №1 (№17)
I. Числовая функция. Способы задания. Монотонность, ограниченность, четность, нечетность функции.
Числовая функция — это функция, области определения и значений которой являются подмножествами числовых множеств — как правило, множества вещественных чисел или множества комплексных чисел.
1. Аналитический способ - задание функции с помощью формулы (или формул). Напр: у=2х, или х2 и.д. y=x√y=|xl
2. Графический способ - задание функции с помощью графика. Если дана функция y=f(x),x∈X и на координатной плоскости xOy отмечены все точки вида (x;y), где x∈X, а y=f(x), то множество этих точек называют графиком функции y=f(x),x∈X. y=kx+m - прямая
3.Словесный (описательный) –с помощью словесного описания. Напр: Каждому действительному аргументу Х ставится в соответствии его удвоенное значение. Если Х=3,то У=3, и т. Д.
4. Табличный – задание функции с помощью таблицы.
Областью определения функции y=f(x) называют множество всех значений x, для которых функция имеет смысл.
Множество всех значений функции y=f(x), x∈X называют областью значений функции.
Монотонность – говорят что функция возрастает на[а;б] если из неравенства x1<x2 -> f(x1)<f(x2) говорят что функция убывает на[а;б] если из неравенства x1<x2 -> f(x1)>f(x2). график чётной функции симметричен относительно оY
график не чётной функции симметричен относительно точки [0;0]. Ограниченности. С геометрической точки зрения- это означает, что график функции расположен между параллельными горизонтальными прямыми
пример: y=sin(x) -1≤sin(x)≤1.В некоторых случаях речь идёт об граничных точках только с верху или только с низу в этом случаи для всех х ϵ множеству Х f(x)≤B или Х f(x)≥А пример: x^
 -нечет.
-нечет.
 - четн.
- четн.
 - Ф.О.В
- Ф.О.В
 -Ф.О.В (функц.общего вида)
-Ф.О.В (функц.общего вида)
Билет№2
1) Степень с произвольным действительным показателем и его свойства.
Можно определить степень  не только для рационального, но и для любого действительного показателя x. Для этого рассматривают последовательность рациональных приближений к числу x, т. е. последовательность рациональных чисел
не только для рационального, но и для любого действительного показателя x. Для этого рассматривают последовательность рациональных приближений к числу x, т. е. последовательность рациональных чисел  которые задают число x с любой степенью точности. Затем вычисляют степени с рациональными показателями
которые задают число x с любой степенью точности. Затем вычисляют степени с рациональными показателями  Оказывается, что эти числа являются приближениями к некоторому числу y, причём, уточнением рационального приближения числа x можно добиться вычисления
Оказывается, что эти числа являются приближениями к некоторому числу y, причём, уточнением рационального приближения числа x можно добиться вычисления  с любой степенью точности. Это число и считают степенью
с любой степенью точности. Это число и считают степенью  с показателем x.
с показателем x.
Свойства степени с действительным показателем
На степени с действительными показателями переносятся все свойства степеней с рациональными показателями.
1) 
2) 
3) 
4) 
5) 
6) 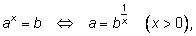
7)  при любом действительном x,
при любом действительном x,
8) пусть  Если
Если  то
то  если
если  то
то 
Основания степеней везде считаются положительными.
Аксиомы стереометрии. Параллельность прямой и плоскости.
Аксиомы стереометрии состоят из 9 аксиом планиметрии и 3 аксиом группы С
Аксиомы группы С
1. Какова бы ни была плоскость, существуют точки в пространстве, принадлежащие этой плоскости, и точки, не принадлежащие ей.
2. Если две разные плоскости имеют общую точку, то они имеют и общую прямую, проходящую через эту точку.
3. Если две разные прямые имеют общую точку, то через них можно провести плоскость, и притом единственную.
4. Для произвольной плоскости выполняются аксиомы планиметрии.
Аксиомы стереометрии.
1. Какова не была прямая сущ. 2 точки, принадлежащие ей и не принадлежащие. Через любые 2 точки можно провести прямую, и только одну.
2. Прямая разбивает плоскость на 2 полуплоскости.
3. На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины и только один.
4. Из 3 точек на прямой и только 1 лежит между двумя.
Билет№3 (№18)
1) Логарифмы. десятичные и натуральные лагорифм ы
Логарифм, взятый по основанию 10, носит название — десятичный логарифм.
Десятичные логарифмы принято обозначать так: lg. Десятичный логарифм единицы равен нулю.
Десятичный логарифм чисел 10, 100, 1000 равен соответвенно 1, 2, 3, и т.д. т.е., имеют столько положительных единиц, сколько нулей стоит после единицы.
Десятичный логарифм чисел 0.1, 0.01, 0.001 равен соответвенно -1,-2, -3, и т.д. т.е. имеют столько отрицательных единиц сколько нулей стоит перед единицей, считая и ноль целых.
Десятичный логарифм других чисел имеет дробную часть. log10(N) = lg N.
Натуральный логарифм — это логарифм по основанию e, где e -иррациональная константа, равная приблизительно 2,718281828. Натуральный логарифм обычно обозначают как ln(x), loge(x) или иногда просто log(x), если основание e подразумевается.
2) Пирамида. Усеченная пирамида.
Пирамида - тело поверхность которого состоит из основания, точки основания не лежащей на основ. И всех отрезков соединяющих вершину пирамиды с точками основания.
Высота пирамиды -перпендикуляр опущенный из вершины пирамиды к основанию.
Апофемой -высота боковой грани.
Усеченная пирамида -тело заключенное между 2-мя основаниями. 
Билет№4
❶ Определение. Функция F (x) называется первообразной для функции f (x) на данном промежутке, если для любого х из данного промежутка F'(x)= f (x). Основное свойство первообразных. Если F (x) – первообразная функции f (x), то и функция F (x)+ C, где C –произвольная постоянная, также является первообразной функции f (x) (т.е. все первообразные функции f(x) записываются в виде F(x) + С).
Геометрическая интерпретация. Графики всех первообразных данной функции f (x) получаются из графика какой-либо одной первообразной параллельными переносами вдоль оси Оу.

Таблица первообразных.

Правила нахождения первообразных. Пусть F(x) и G(x) – первообразные соответственно функций f(x) и g(x). Тогда:
1. F (x) ± G (x) – первообразная для f (x) ± g (x);
2. а F (x) – первообразная для а f (x);
3.  – первообразная для а f (kx + b).
– первообразная для а f (kx + b).
❷ Конусом называется тело, состоящее из основания, точки не лежащей на основании (вершина конуса), и всех отрезков соединяющих вершину конуса с точками основания (образующая). Высотой конуса называется перпендикуляр опущенный из вершины конуса к основанию (Sбоковое= ПRL). Усеченным конусом называется тело, заключенное между двумя основаниями. (Sбоковое= П (R1+R2) ×L.
Билет№5
1)Неопределенный интеграл и его свойства: Множество всех первообразных некоторой функции f (x) называется неопределенным интегралом функции f (x) и обозначается как 
Таким образом, если F - некоторая частная первообразная, то справедливо выражение
 где С - произвольная постоянная.
где С - произвольная постоянная.
Свойства неопределенного интеграла
В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f,
а, k, C - постоянные величины.




Усеченный конус. Конус.
Конус – тело состоящее из основани, точки не лежащей на основании(вершина конуса) и всех отрезков соединяющих вершину конуса с точками основания.(образующие)
Высотой конуса называют перпендикуляр опущенный из вершины к основанию.
Усеченный конус - тело заключенное между 2 мя основаниями.
Sбок=ПRL
Sбок.усечен.= П(R1 +R2)L
Билет№6
1) Показательная и логарифмическая функция,свойства и графики: Показательная функция, такая функция, которая может быть задана формулой 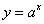 , где а - любое положительное число, не равное единице.
, где а - любое положительное число, не равное единице.
Билет№7
1) Свойства и графики тригонометрической функции: Основными тригонометрическими функциями являются функции y=sin(x), y=cos(x), y=tg(x), y=ctg(x). Рассмотрим каждую из них в отдельности.
Y = sin(x)
График функции y=sin(x).

Основные свойства:
1. Область определения вся числовая ось.
2. Функция ограниченная. Множество значений – отрезок [-1;1].
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным 2*π.
Y = cos(x)
График функции y=cos(x).
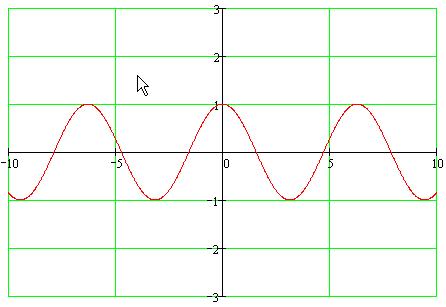
Основные свойства:
1. Область определения вся числовая ось.
2. Функция ограниченная. Множество значений – отрезок [-1;1].
3. Функция четная.
4.Функция периодическая с наименьшим положительным периодом равным 2*π.
Y = tg(x)
График функции y=tg(x).

Основные свойства:
1. Область определения вся числовая ось, за исключением точек вида x=π/2 +π*k, где k – целое.
2. Функция неограниченная. Множество значение вся числовая прямая.
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным π.
Y = ctg(x)
График функции y=ctg(x).

2) Вектор. Векторы на плоскости и в пространстве. Действие над векторами:
3) Вектор — это направленный отрезок имеющий начало и конец.
4) Длинна вектора - абсолютная величина. Равными называются векторы, имеющие одинаковые длины и одинаковое направление. Это значит, что вектор можно перенести параллельно себе в любую точку плоскости.
Единичным называется вектор, длина которого равна 1 . Нулевым — вектор, длина которого равна нулю, то есть его начало совпадает с концом.
5) Сложения векторов — правило треугольника. Возьмем те же векторы  и
и  . К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов
. К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов  и
и  .
. 

Вычитание. Вектор  направлен противоположно вектору
направлен противоположно вектору  . Длины векторов
. Длины векторов  и
и  равны.
равны.

Теперь понятно, что такое вычитание векторов. Разность векторов  и
и  — это сумма вектора
— это сумма вектора  и вектора
и вектора  .
. 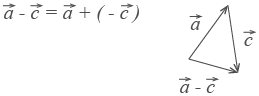
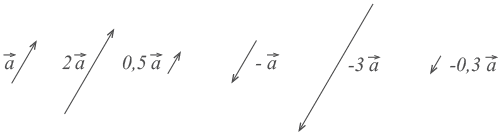
При умножении вектора  на число k получается вектор, длина которого в k раз отличается от длины
на число k получается вектор, длина которого в k раз отличается от длины  . Он сонаправлен с вектором
. Он сонаправлен с вектором  , если k больше нуля, и направлен противоположно
, если k больше нуля, и направлен противоположно  , если k меньше нуля.
, если k меньше нуля.
Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.

Билет№8
1)Проиводная, ее геометрический и физический смысл. Производная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке
 Уравнение касательной к графику функции y=f(x) в точке x0:
Уравнение касательной к графику функции y=f(x) в точке x0:
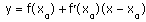 Физический смысл производной.
Физический смысл производной.
Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:

2)Геометрические тела. Многогранники:
Геометрия – это наука изучающая св – во геометрических фигур.
Геометрическое тело — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.
Многогранник – это такое тело, поверхность которого состоит из конечного числа плоских многоугольников
Куб – правильный четырех угольник. 8 вершин, 6 граней, 12 ребер.
5 видов правильных многоугольников: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.
Тетраэдр  , октаэдр
, октаэдр  , додекаэдр
, додекаэдр  .
.
Билет №9(20)
Известно, что каким бы ни было действительное число t, ему можно поставить в соответствие однозначно определённое число sint.
Правило соответствия следующее: нужно
1. расположить числовую окружность на координатной плоскости так, чтобы центр окружности совпал с началом координат, а начальная точка A окружности попала в точку (1;0);
2. на окружности найти точку, соответствующую числу t;
3. найти ординату этой точки, которая и есть sint.
Это и будет функция s=sint,t∈R
Аналогично можно сказать ещё о трёх функциях:
s=cost;s=tgt;s=ctgt.
Все эти функции называют тригонометрическими функциями числового аргумента t.
Есть равенства, связывающие значения различных тригонометрических функций. Некоторые из этих равенств уже известны:
sin2t+cos2t=1;tgt=sintcost,t≠π2+πk;ctgt=costsint,t≠πk,k∈Z.
Из двух последних равенств получим соотношение, связывающее tgt и ctgt:
tgt⋅ctgt=1,t≠πk2,k∈Z.
Выполняя преобразования, можно получить ещё две важные формулы:1+tg2t=1cos2t,t≠π2+πk;1+ctg2t=1sin2t,t≠πk,k∈Z.
| Связь между тригонометрическими функциями одного и того же аргумента:
|
Билет№10(16)
1) Определеный интеграл и его значение:Определенным интегралом от a до b непрерывной функции y=f(x), определенной на интервале [a;b], называется приращение первообразной F(x) для этой функции, то есть

Числа a и b называются нижним и верхним пределами интегрирования.
Площать S криволинейной трапеции (фируры, ограниченной графиком непрерывной положительной на интервале [a;b] функции y=f(x), осью OX и прямыми x = a и x = b вычисляется по формуле:

2) Шар и Сфера:
Сфе́ра — это геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки (центра сферы). Расстояние от точек сферы до её центра называется радиусом сферы и обычно обозначается R. Радиусом также называется любой отрезок, соединяющий точку сферы с её центром. Сфера – это граница шара. Центр, радиус и диаметр сферы являются также центром, радиусом и диаметром шара. Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии не более чем на данное расстояние. Другими словами, шар – это объединение сферы и всех ее внутренних точек.


Шар Сфера
Билет№11
1) Системы уравнений и неравенств. Способы решения систем уравнений(подстановкой,сложения, графический, с Крамера) Метод подстановки.  1.Выразить у через х из одного уравнения системы.
1.Выразить у через х из одного уравнения системы.
2.Подставить полученное выражение вместо у в другое уравнение системы.3.Решить полученное уравнение относительно х.4.Подставить поочередно каждый из найденных на 3 шаге корней уравнения вместо х в выражение у через х, полученное на первом шаге.5.Записать ответ в виде пар значений (х;у). Метод Крамера Одним из основных методов решения данной системы является метод Крамера или метод определителей. По коэффициентам данной системы составляем три определителя:  (главный),
(главный),  х – определитель неизвестного х;
х – определитель неизвестного х;  у – определитель неизвестного у.
у – определитель неизвестного у.
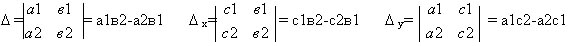

Билет №12(15)
Схема исследования функции
- Найти область определения функции;
- Исследовать функцию на четность, нечетность, периодичность;
3. Найти точки пересечения графика функции с осями координат;
4. Исследовать функцию на монотонность, то есть найти промежутки возрастания и убывания функции;
5. Найти точки экстремума и экстремальные значения функции;
Построить график функции.
Билет
1)Производная. Ее геометрический и физический смысл.
Физический (механический) смысл производной состоит в следующем. Если s(t) — закон прямолинейного движения тела, то производная выражает мгновенную скорость в момент времени t: v=s′(t).
Величина тока.
Геометрический смысл производной состоит в следующем. Если к графику функции y=f(x) в точке с абсциссой x=a можно провести касательную, непараллельную оси y, то f′(a) выражает угловой коэффициент касательной:
k=f′(a).
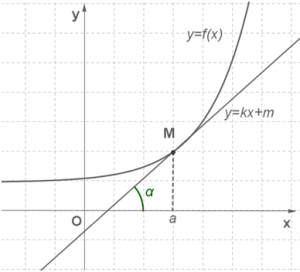
Поскольку k=tgα, то верно равенство f′(a)=tgα.
2) Вероятность
Теория вероятностей — это область математики, которая изучает случайные события и общие свойства событий, процессов.
В теории вероятностей эксперименты называются опытами, а возможные результаты — исходами. Все возможные исходы вместе создают множество исходов.
Любое утверждение о результате опыта, правильность которого возможно проверить, называется событием.
Событие, которое не может произойти, называется невозможным событием.
Событие, которое происходит всегда, называется достоверным событием.
Усло́вная вероя́тность — вероятность одного события при условии, что другое событие уже произошло.
Теорема. Вероятность суммы конечного числа несовместных событий  равна сумме вероятностей этих событий
равна сумме вероятностей этих событий
Теорема сложения вероятностей позволяет вычислять вероятности суммы двух или нескольких событий. Для двух событий теорема формулируется следующим образом.
Вероятность суммы двух событий равна сумме вероятностей этих событий минус вероятность их произведения: P(A+B)= P(A) + P(B) – P(AB).
Билет№14
1) Системы уравнений и неравенств. Способы решения систем уравнений(подстановкой,сложения, графический, с Крамера) Метод подстановки.  1.Выразить у через х из одного уравнения системы.
1.Выразить у через х из одного уравнения системы.
2.Подставить полученное выражение вместо у в другое уравнение системы.3.Решить полученное уравнение относительно х.4.Подставить поочередно каждый из найденных на 3 шаге корней уравнения вместо х в выражение у через х, полученное на первом шаге.5.Записать ответ в виде пар значений (х;у). Метод Крамера Одним из основных методов решения данной системы является метод Крамера или метод определителей. По коэффициентам данной системы составляем три определителя:  (главный),
(главный),  х – определитель неизвестного х;
х – определитель неизвестного х;  у – определитель неизвестного у.
у – определитель неизвестного у.
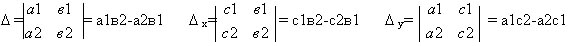

❷Признаки перпендикулярности прямой и плоскости: 1) Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости. 2) Если плоскость перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой. Наклонная к плоскости. Прямая, пересекающая плоскость и не перпендикулярная ей, называется наклонной к плоскости. Теорема о трех перпендикулярах. Наклонная к плоскости перпендикулярна к прямой, лежащей в этой плоскости, тогда и только тогда, когда проекция наклонной перпендикулярна этой прямой. Теорема, обратная теореме о трех перпендикулярах. Прямая, проведённая в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к её проекции.
Признак перпендикулярности плоскостей: если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны. Теорема об общем перпендикуляре к двум скрещивающимся прямым. Для любых двух скрещивающихся прямых существует единственный общий перпендикуляр.
Билет№19
1) Системы уравнений и неравенств. Способы решения систем уравнений(подстановкой,сложения, графический, с Крамера) Метод подстановки.  1.Выразить у через х из одного уравнения системы.
1.Выразить у через х из одного уравнения системы.
2.Подставить полученное выражение вместо у в другое уравнение системы.3.Решить полученное уравнение относительно х.4.Подставить поочередно каждый из найденных на 3 шаге корней уравнения вместо х в выражение у через х, полученное на первом шаге.5.Записать ответ в виде пар значений (х;у). Метод Крамера Одним из основных методов решения данной системы является метод Крамера или метод определителей. По коэффициентам данной системы составляем три определителя:  (главный),
(главный),  х – определитель неизвестного х;
х – определитель неизвестного х;  у – определитель неизвестного у.
у – определитель неизвестного у.
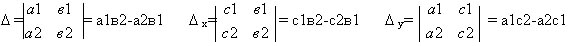

Билет №1 (№17)
I. Числовая функция. Способы задания. Монотонность, ограниченность, четность, нечетность функции.
Числовая функция — это функция, области определения и значений которой являются подмножествами числовых множеств — как правило, множества вещественных чисел или множества комплексных чисел.
1. Аналитический способ - задание функции с помощью формулы (или формул). Напр: у=2х, или х2 и.д. y=x√y=|xl
2. Графический способ - задание функции с помощью графика. Если дана функция y=f(x),x∈X и на координатной плоскости xOy отмечены все точки вида (x;y), где x∈X, а y=f(x), то множество этих точек называют графиком функции y=f(x),x∈X. y=kx+m - прямая
3.Словесный (описательный) –с помощью словесного описания. Напр: Каждому действительному аргументу Х ставится в соответствии его удвоенное значение. Если Х=3,то У=3, и т. Д.
4. Табличный – задание функции с помощью таблицы.
Областью определения функции y=f(x) называют множество всех значений x, для которых функция имеет смысл.
Множество всех значений функции y=f(x), x∈X называют областью значений функции.
Монотонность – говорят что функция возрастает на[а;б] если из неравенства x1<x2 -> f(x1)<f(x2) говорят что функция убывает на[а;б] если из неравенства x1<x2 -> f(x1)>f(x2). график чётной функции симметричен относительно оY
график не чётной функции симметричен относительно точки [0;0]. Ограниченности. С геометрической точки зрения- это означает, что график функции расположен между параллельными горизонтальными прямыми
пример: y=sin(x) -1≤sin(x)≤1.В некоторых случаях речь идёт об граничных точках только с верху или только с низу в этом случаи для всех х ϵ множеству Х f(x)≤B или Х f(x)≥А пример: x^
 -нечет.
-нечет.
 - четн.
- четн.
 - Ф.О.В
- Ф.О.В
 -Ф.О.В (функц.общего вида)
-Ф.О.В (функц.общего вида)
II. Геометрические тела. Многогранники. Призма. Параллелепипед и его свойства.
Геометрия – это наука изучающая св – во геометрических фигур.
Геометрическое тело — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.
Наружная граница геометрического тела является его гранью, у тела может быть одна либо несколько граней. Множество плоских граней определяет множество вершин и ребер геометрического тела.
| Тела вращения — это объёмные тела, которые возникают следствием вращения плоской геометрической фигуры, которая ограничена кривой, вокруг оси. Эта ось лежит в той же плоскости.
|
Многогранник – это такое тело, поверхность которого состоит из конечного числа плоских многоугольников
Куб – правильный четырех угольник. 8 вершин, 6 граней, 12 ребер.
5 видов правильных многоугольников: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.
Тетраэдр  , октаэдр
, октаэдр  , додекаэдр
, додекаэдр  .
.
Призма – это многогранник состоит из 2-х плоских многоугольн., лежащих в разных плоскостях и совмещенных параллельным переносом. (4-х угольная призма и 3-х)
Высотой призмы – называется расстояние между 2-мя основаниями.
Призма назыв. прямой, если ее боковые ребра перпендикулярны основаниям, в противном случае прямой.
Полная поверхность призмы равна сумме боковых поверхностей и площадей оснований.
Sполн.= 2 Sосн. + Sбок.
SБок.= P осн.*h
Параллелепипед (от греч. — параллельный, плоскость) — призма, основанием которой служит параллелограмм.
Типы параллелепипедов
прямые и наклонные.
Прямым параллелепипедом называется прямая призма, основание которой — параллелограмм.
Свойства
1.Параллелепипед симметричен относительно середины его диагонали, соединяющей противоположные вершины.
2.Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
3.Противолежащие грани параллелепипеда параллельны и равны.
4. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
5. Аффинное преобразование всегда переводит параллелепипед в параллелепипед. Для любого параллелепипеда существует аффинное преобразование, которое преобразует его в куб.
Билет№2
1) Степень с произвольным действительным показателем и его свойства.
Можно определить степень  не только для рационального, но и для любого действительного показателя x. Для этого рассматривают последовательность рациональных приближений к числу x, т. е. последовательность рациональных чисел
не только для рационального, но и для любого действительного показателя x. Для этого рассматривают последовательность рациональных приближений к числу x, т. е. последовательность рациональных чисел  которые задают число x с любой степенью точности. Затем вычисляют степени с рациональными показателями
которые задают число x с любой степенью точности. Затем вычисляют степени с рациональными показателями  Оказывается, что эти числа являются приближениями к некоторому числу y, причём, уточнением рационального приближения числа x можно добиться вычисления
Оказывается, что эти числа являются приближениями к некоторому числу y, причём, уточнением рационального приближения числа x можно добиться вычисления  с любой степенью точности. Это число и считают степенью
с любой степенью точности. Это число и считают степенью  с показателем x.
с показателем x.
Свойства степени с действительным показателем
На степени с действительными показателями переносятся все свойства степеней с рациональными показателями.
1) 
2) 
3) 
4) 
5) 
6) 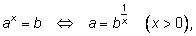
7)  при любом действительном x,
при любом действительном x,
8) пусть  Если
Если  то
то  если
если  то
то 
Основания степеней везде считаются положительными.



 -нечет.
-нечет. - четн.
- четн. - Ф.О.В
- Ф.О.В -Ф.О.В (функц.общего вида)
-Ф.О.В (функц.общего вида) не только для рационального, но и для любого действительного показателя x. Для этого рассматривают последовательность рациональных приближений к числу x, т. е. последовательность рациональных чисел
не только для рационального, но и для любого действительного показателя x. Для этого рассматривают последовательность рациональных приближений к числу x, т. е. последовательность рациональных чисел  которые задают число x с любой степенью точности. Затем вычисляют степени с рациональными показателями
которые задают число x с любой степенью точности. Затем вычисляют степени с рациональными показателями  Оказывается, что эти числа являются приближениями к некоторому числу y, причём, уточнением рационального приближения числа x можно добиться вычисления
Оказывается, что эти числа являются приближениями к некоторому числу y, причём, уточнением рационального приближения числа x можно добиться вычисления  с любой степенью точности. Это число и считают степенью
с любой степенью точности. Это число и считают степенью 




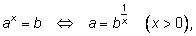
 при любом действительном x,
при любом действительном x, Если
Если  то
то  если
если  то
то 



 – первообразная для а f (kx + b).
– первообразная для а f (kx + b).
 где С - произвольная постоянная.
где С - произвольная постоянная. 



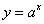 , где а - любое положительное число, не равное единице.
, где а - любое положительное число, не равное единице.



 и
и  . К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов
. К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов 

 направлен противоположно вектору
направлен противоположно вектору  . Длины векторов
. Длины векторов 
 .
. 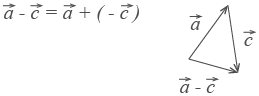


 Уравнение касательной к графику функции y=f(x) в точке x0:
Уравнение касательной к графику функции y=f(x) в точке x0: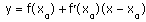 Физический смысл производной.
Физический смысл производной.
 , октаэдр
, октаэдр  , додекаэдр
, додекаэдр  .
.
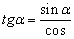

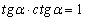

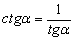
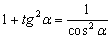









 1.Выразить у через х из одного уравнения системы.
1.Выразить у через х из одного уравнения системы. (главный),
(главный),  х – определитель неизвестного х;
х – определитель неизвестного х; 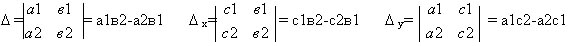


 равна сумме вероятностей этих событий
равна сумме вероятностей этих событий


