Рациональной называется функция, представимая в виде дроби  , где
, где  и
и  -- многочлены. Рациональная дробь называется правильной если степень многочлена, стоящего в числителе, меньше степени многочлена в знаменателе. В противном случае рациональная дробь называется неправильной. Рассмотрим сначала два частных случая интегрирования правильной рациональной дроби, когда в знаменателе стоит многочлен второй степени.
-- многочлены. Рациональная дробь называется правильной если степень многочлена, стоящего в числителе, меньше степени многочлена в знаменателе. В противном случае рациональная дробь называется неправильной. Рассмотрим сначала два частных случая интегрирования правильной рациональной дроби, когда в знаменателе стоит многочлен второй степени.
1)  . В этом случае нужно в знаменателе выделить полный квадрат.
. В этом случае нужно в знаменателе выделить полный квадрат.
Пример 1.21. Вычислить  .
.
Выделим в знаменателе квадрат суммы, получим

 .
.
2)  . Чтобы вычислить такого типа интеграл, нужно в числителе выделить производную знаменателя.
. Чтобы вычислить такого типа интеграл, нужно в числителе выделить производную знаменателя.
Пример 1.22. Вычислить  .
.
Найдем производную знаменателя:  . Для того, чтобы выделить такое же выражение в числителе, умножим и разделим числитель на 2. Получим
. Для того, чтобы выделить такое же выражение в числителе, умножим и разделим числитель на 2. Получим
 В первом интеграле многочлен, стоящий в числителе внесем под знак дифференциала, а второй интеграл после вынесения постоянного множителя 6 за интеграл, станет интегралом первого типа, рассмотренного выше. Тогда
В первом интеграле многочлен, стоящий в числителе внесем под знак дифференциала, а второй интеграл после вынесения постоянного множителя 6 за интеграл, станет интегралом первого типа, рассмотренного выше. Тогда

 .
.
Если знаменатель  правильной рациональной дроби степени выше, чем вторая, то он может быть представлен в виде
правильной рациональной дроби степени выше, чем вторая, то он может быть представлен в виде
 ,
,
где А – коэффициент при старшей степени многочлена  -- корни уравнения
-- корни уравнения  , а трехчлены не имеют действительных корней. Тогда эта дробь разлагается на сумму элементарных дробей следующим образом:
, а трехчлены не имеют действительных корней. Тогда эта дробь разлагается на сумму элементарных дробей следующим образом:

 (1.4),
(1.4),
где  -- некоторые неизвестные числа (коэффициенты). Для их определения умножаем обе части последнего равенства на
-- некоторые неизвестные числа (коэффициенты). Для их определения умножаем обе части последнего равенства на  . Получаем равенство двух многочленов. Далее, приравнивая между собой коэффициенты при одинаковых степенях в левой и правой частях, получим систему линейных уравнений, из которой найдем неизвестные числа.
. Получаем равенство двух многочленов. Далее, приравнивая между собой коэффициенты при одинаковых степенях в левой и правой частях, получим систему линейных уравнений, из которой найдем неизвестные числа.
Заметим, что после умножения на  , в случае, когда
, в случае, когда  имеет действительные корни, целесообразно подставить в обе части получившегося равенства последовательно эти корни. В результате найдем часть неизвестных чисел. Изложенный метод отыскания разложения рациональной функции называется методом неопределенных коэффициентов.
имеет действительные корни, целесообразно подставить в обе части получившегося равенства последовательно эти корни. В результате найдем часть неизвестных чисел. Изложенный метод отыскания разложения рациональной функции называется методом неопределенных коэффициентов.
Если рациональная дробь неправильная, то всегда с помощью деления многочлена  на
на  можем представить
можем представить  , где
, где  --многочлен, а
--многочлен, а  --- правильная рациональная дробь.
--- правильная рациональная дробь.
Пример 1.23. Вычислить  .
.
Подынтегральная функция – правильная рациональная дробь. Так как  не имеет действительных корней, то по формуле (1.4) имеем
не имеет действительных корней, то по формуле (1.4) имеем
 , где
, где  --- неизвестные коэффициенты. Умножая обе части равенства на
--- неизвестные коэффициенты. Умножая обе части равенства на  , получаем
, получаем
 , или
, или
 .
.
Приравнивая коэффициенты при одинаковых степенях 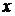 , придем к системе уравнений
, придем к системе уравнений

Решая эту систему, найдем  . Искомое разложение имеет вид:
. Искомое разложение имеет вид:  . Следовательно,
. Следовательно,

 .
.
Пример 1.24. Вычислить  .
.
Подынтегральная функция – правильная рациональная дробь. Так как  , причем второй сомножитель не имеет действительных корней, то по формуле (1.4) имеем
, причем второй сомножитель не имеет действительных корней, то по формуле (1.4) имеем  , где
, где  -- неизвестные коэффициенты. Умножая обе части равенства на
-- неизвестные коэффициенты. Умножая обе части равенства на  , получаем
, получаем 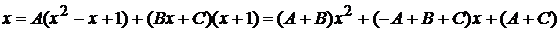 .
.
Приравнивая коэффициенты при одинаковых степенях 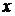 и решая систему уравнений, получим
и решая систему уравнений, получим  . Таким образом,
. Таким образом,



 .
.
Обратите внимание, последний интеграл в этом соотношении оказался интегралом первого типа из рассматриваемых нами выше, поэтому для его вычисления мы в квадратном трехчлене  выделили полный квадрат.
выделили полный квадрат.
Пример 1.25. Вычислить  .
.
Подынтегральная функция --- неправильная рациональная дробь, поэтому выделим ее целую часть делением числителя на знаменатель. В результате получим:  . Полученную справа правильную дробь разложим на простые дроби.
. Полученную справа правильную дробь разложим на простые дроби.  .
.
Отсюда  . Полагая
. Полагая  , находим
, находим  . Сравнивая коэффициенты при одинаковых степенях
. Сравнивая коэффициенты при одинаковых степенях 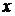 , получим
, получим

Следовательно,  . Далее, находим
. Далее, находим


 .
.
Пример 1.26. Вычислить 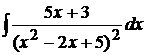 .
.
В числителе подынтегральной функции выделим производную квадратного трехчлена, стоящего в знаменателе 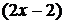 .
.


 .
.
При вычислении последнего интеграла мы воспользовались формулой (1.3).
Упражнения.
1.4. Вычислить интегралы (в скобках указаны ответы).
1).  ;
;
2).  ;
;
3).  ;
;
4).  ;
;
5).  ;
;
6). 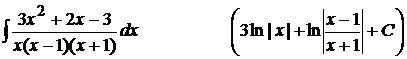 ;
;
7). 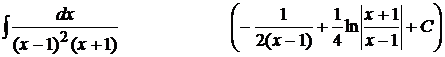 ;
;
8).  ;
;
9). 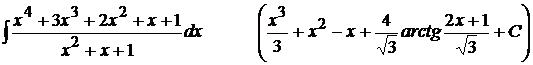 ;
;
10).  ;
;
11).  ;
;
12).  ;
;
13).  ;
;
14). 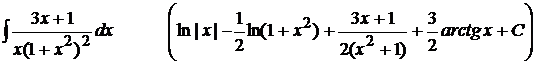 ;
;
15). 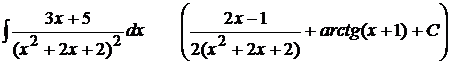 .
.
1.5. Нахождение интегралов вида 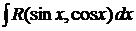 .
.
Отметим, что R обозначает рациональную функцию своих аргументов  и
и  . Эти интегралы сводятся к интегралам от рациональной функции с помощью так называемой универсальной подстановки
. Эти интегралы сводятся к интегралам от рациональной функции с помощью так называемой универсальной подстановки  .
.
Так как  , то
, то  .
.  .
.
 .
.
Пример 1.27. Вычислить
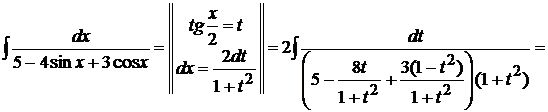
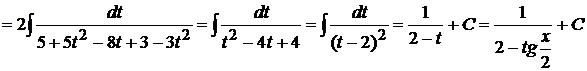 .
.
Однако на практике универсальная подстановка часто приводит к слишком сложным и трудоемким выкладкам, поэтому наряду с универсальной подстановкой полезно знать и другие постановки, которые во многих случаях быстрее приводят к цели.
Если функция 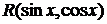 нечетна относительно
нечетна относительно  , то есть
, то есть 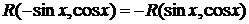 , то рационализация интеграла достигается с помощью подстановки
, то рационализация интеграла достигается с помощью подстановки 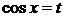 .
.
Если функция 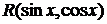 нечетна относительно
нечетна относительно  , то используется подстановка
, то используется подстановка 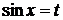 .
.
Если функция 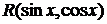 четна относительно
четна относительно  и
и  , то есть
, то есть  , то целесообразна подстановка
, то целесообразна подстановка 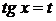 .
.
Пример 1.28. Вычислить

 .
.
Пример 1.29. Вычислить

 .
.
Иногда при вычислении интегралов указанного вида бывает полезно прибегать и к другим искусственным приемам, используя известные тригонометрические формулы, как, например, формулу  .
.
Пример 1.30. Вычислить
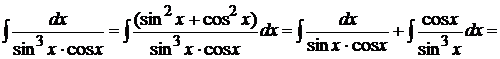
 .
.
Замечание 1. Если в интеграле вида  оба показателя степени m и n положительны и четны, то целесообразно применять формулы
оба показателя степени m и n положительны и четны, то целесообразно применять формулы
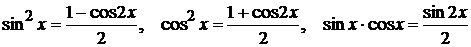 ,
,
которые приводят данный интеграл к интегралу с меньшими неотрицательными показателями.
Замечание 2. Интегралы вида  непосредственно вычисляются с помощью формул:
непосредственно вычисляются с помощью формул: 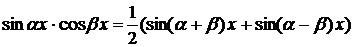 ,
,
 ,
,
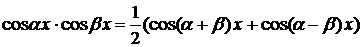 .
.
Пример 1.31. Вычислить



 .
.
Упражнения.
1.5. Вычислить интегралы (в скобках указаны ответы).
1).  ;
;
2).  ;
;
3). 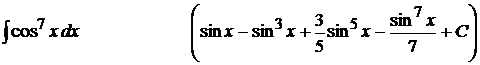 ;
;
4). 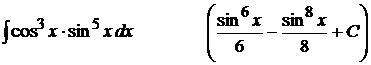 ;
;
5). 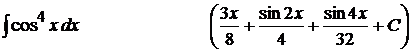 ;
;
6).  ;
;
7).  ;
;
8).  ;
;
9).  ;
;
10). 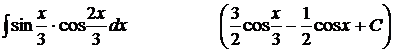 ;
;
11).  ;
;
12).  ;
;
13).  ;
;
14).  ;
;
15). 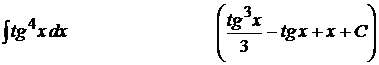 ;
;
16). 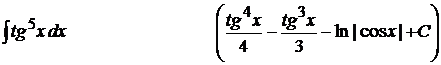 ;
;
17).  ;
;
18). 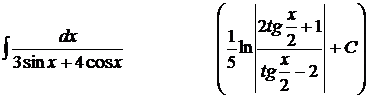 ;
;
19).  ;
;
20). 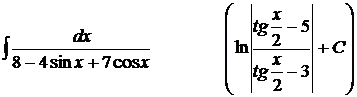 ;
;
21).  ;
;
22).  ;
;
23).  .
.
Определенный интеграл
2.1. Определение определенного интеграла. Пусть функция  определена на отрезке
определена на отрезке 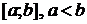 . Разобьем отрезок на
. Разобьем отрезок на 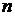 произвольных частей точками
произвольных частей точками  . В каждом из полученных частичных отрезков
. В каждом из полученных частичных отрезков 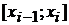 выберем произвольную точку
выберем произвольную точку 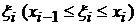 и составим сумму
и составим сумму  , где
, где  . Эта сумма называется интегральной суммой для функции
. Эта сумма называется интегральной суммой для функции  на
на  . Обозначим через
. Обозначим через 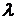 длину наибольшего частичного отрезка разбиения:
длину наибольшего частичного отрезка разбиения:  .
.
Определение 2.1. Если существует конечный предел  интегральной суммы при
интегральной суммы при 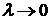 и он не зависит от выбора точек
и он не зависит от выбора точек  , то этот предел называется определенным интегралом от функции
, то этот предел называется определенным интегралом от функции  по отрезку
по отрезку  и обозначается следующим образом:
и обозначается следующим образом:
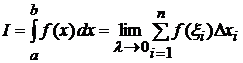 .
.
В этом случае функция  называется интегрируемой на
называется интегрируемой на  . Числа
. Числа  и
и 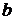 называются соответственно нижним и верхним пределами интегрирования,
называются соответственно нижним и верхним пределами интегрирования,  -- подынтегральной функцией,
-- подынтегральной функцией, 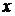 --переменной интегрирования.
--переменной интегрирования.
Для интегрируемости функции достаточно ее непрерывности на  . В дальнейшем будем предполагать, что рассматриваемые функции непрерывны на
. В дальнейшем будем предполагать, что рассматриваемые функции непрерывны на  .
.



 , где
, где  и
и  -- многочлены. Рациональная дробь называется правильной если степень многочлена, стоящего в числителе, меньше степени многочлена в знаменателе. В противном случае рациональная дробь называется неправильной. Рассмотрим сначала два частных случая интегрирования правильной рациональной дроби, когда в знаменателе стоит многочлен второй степени.
-- многочлены. Рациональная дробь называется правильной если степень многочлена, стоящего в числителе, меньше степени многочлена в знаменателе. В противном случае рациональная дробь называется неправильной. Рассмотрим сначала два частных случая интегрирования правильной рациональной дроби, когда в знаменателе стоит многочлен второй степени. . В этом случае нужно в знаменателе выделить полный квадрат.
. В этом случае нужно в знаменателе выделить полный квадрат. .
.
 .
. . Чтобы вычислить такого типа интеграл, нужно в числителе выделить производную знаменателя.
. Чтобы вычислить такого типа интеграл, нужно в числителе выделить производную знаменателя. .
. . Для того, чтобы выделить такое же выражение в числителе, умножим и разделим числитель на 2. Получим
. Для того, чтобы выделить такое же выражение в числителе, умножим и разделим числитель на 2. Получим В первом интеграле многочлен, стоящий в числителе внесем под знак дифференциала, а второй интеграл после вынесения постоянного множителя 6 за интеграл, станет интегралом первого типа, рассмотренного выше. Тогда
В первом интеграле многочлен, стоящий в числителе внесем под знак дифференциала, а второй интеграл после вынесения постоянного множителя 6 за интеграл, станет интегралом первого типа, рассмотренного выше. Тогда
 .
. ,
, -- корни уравнения
-- корни уравнения  , а трехчлены не имеют действительных корней. Тогда эта дробь разлагается на сумму элементарных дробей следующим образом:
, а трехчлены не имеют действительных корней. Тогда эта дробь разлагается на сумму элементарных дробей следующим образом:
 (1.4),
(1.4), -- некоторые неизвестные числа (коэффициенты). Для их определения умножаем обе части последнего равенства на
-- некоторые неизвестные числа (коэффициенты). Для их определения умножаем обе части последнего равенства на  , где
, где  --многочлен, а
--многочлен, а  --- правильная рациональная дробь.
--- правильная рациональная дробь. .
. не имеет действительных корней, то по формуле (1.4) имеем
не имеет действительных корней, то по формуле (1.4) имеем , где
, где  --- неизвестные коэффициенты. Умножая обе части равенства на
--- неизвестные коэффициенты. Умножая обе части равенства на  , получаем
, получаем , или
, или .
.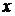 , придем к системе уравнений
, придем к системе уравнений
 . Искомое разложение имеет вид:
. Искомое разложение имеет вид:  . Следовательно,
. Следовательно,
 .
. .
. , причем второй сомножитель не имеет действительных корней, то по формуле (1.4) имеем
, причем второй сомножитель не имеет действительных корней, то по формуле (1.4) имеем  , где
, где  -- неизвестные коэффициенты. Умножая обе части равенства на
-- неизвестные коэффициенты. Умножая обе части равенства на  , получаем
, получаем 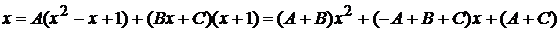 .
. . Таким образом,
. Таким образом,


 .
. выделили полный квадрат.
выделили полный квадрат. .
. . Полученную справа правильную дробь разложим на простые дроби.
. Полученную справа правильную дробь разложим на простые дроби.  .
. . Полагая
. Полагая  , находим
, находим  . Сравнивая коэффициенты при одинаковых степенях
. Сравнивая коэффициенты при одинаковых степенях 
 . Далее, находим
. Далее, находим

 .
.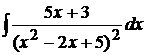 .
.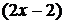 .
.

 .
. ;
; ;
; ;
; ;
; ;
;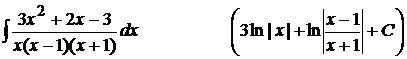 ;
;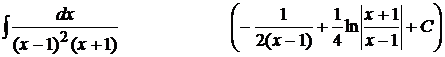 ;
; ;
;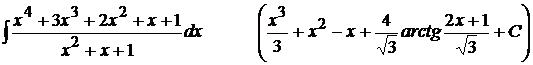 ;
; ;
; ;
; ;
; ;
;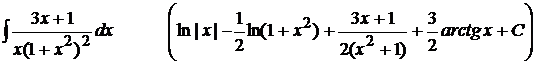 ;
;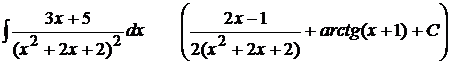 .
. .
. и
и  . Эти интегралы сводятся к интегралам от рациональной функции с помощью так называемой универсальной подстановки
. Эти интегралы сводятся к интегралам от рациональной функции с помощью так называемой универсальной подстановки  .
. , то
, то  .
.  .
. .
.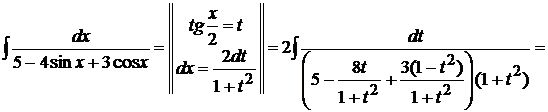
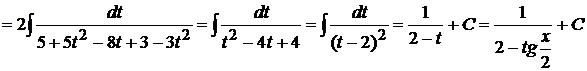 .
.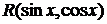 нечетна относительно
нечетна относительно 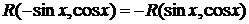 , то рационализация интеграла достигается с помощью подстановки
, то рационализация интеграла достигается с помощью подстановки 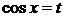 .
.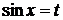 .
. , то целесообразна подстановка
, то целесообразна подстановка 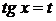 .
.
 .
.
 .
. .
.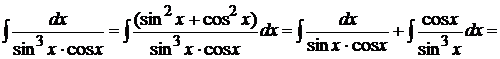
 .
. оба показателя степени m и n положительны и четны, то целесообразно применять формулы
оба показателя степени m и n положительны и четны, то целесообразно применять формулы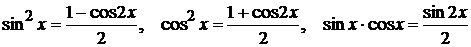 ,
, непосредственно вычисляются с помощью формул:
непосредственно вычисляются с помощью формул: 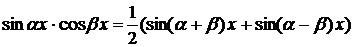 ,
, ,
,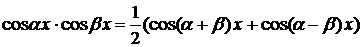 .
.


 .
. ;
; ;
;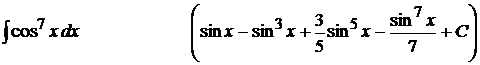 ;
;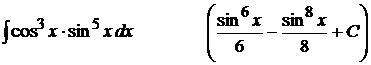 ;
;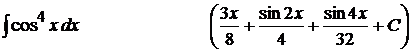 ;
; ;
; ;
; ;
; ;
;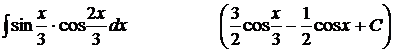 ;
; ;
; ;
; ;
; ;
;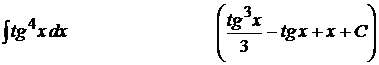 ;
;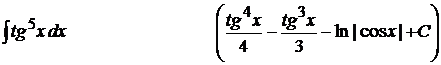 ;
; ;
;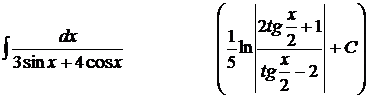 ;
; ;
;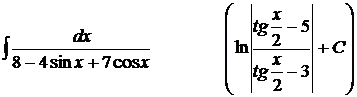 ;
; ;
; ;
; .
. определена на отрезке
определена на отрезке 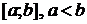 . Разобьем отрезок на
. Разобьем отрезок на 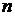 произвольных частей точками
произвольных частей точками  . В каждом из полученных частичных отрезков
. В каждом из полученных частичных отрезков 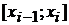 выберем произвольную точку
выберем произвольную точку 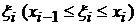 и составим сумму
и составим сумму  , где
, где  . Эта сумма называется интегральной суммой для функции
. Эта сумма называется интегральной суммой для функции  . Обозначим через
. Обозначим через 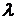 длину наибольшего частичного отрезка разбиения:
длину наибольшего частичного отрезка разбиения:  .
. интегральной суммы при
интегральной суммы при 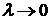 и он не зависит от выбора точек
и он не зависит от выбора точек  , то этот предел называется определенным интегралом от функции
, то этот предел называется определенным интегралом от функции 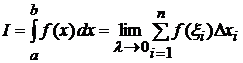 .
. и
и 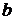 называются соответственно нижним и верхним пределами интегрирования,
называются соответственно нижним и верхним пределами интегрирования,