Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.
Непрерывную случайную величину можно задать с помощью функции распределения
F (x) = P (X< x)
Геометрически это равенство можно истолковать так: F (x) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
Рассмотрим свойства функции распределения.
Свойство 1. Значения функции распределения принадлежат отрезку [0,1]:
 .
.
Свойство 2. F (x) – неубывающая функция, т.е.
 , если
, если  .
.
Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале:
 .
.
Следствие 2. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.
Свойство 3. Если возможные значения случайной величины принадлежат интервалу (a, b),то 1) F (x)=0 при 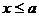 ;
;
2) F (x)=1 при  .
.
Следствие. Если возможные значения непрерывной случайной величины расположены на всей оси х, то справедливы следующие предельные соотношения:
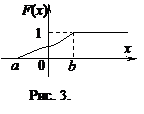
 F (x)=0;
F (x)=0;  F (x)=1.
F (x)=1.
График функции распределения непрерывной случайной величины расположен в полосе, ограниченной прямыми у =0, у =1 и изображен на рис.3.
Непрерывную случайную величину можно задать, используя кроме функции распределения F (x), функцию, называемую плотностью распределения или плотностью вероятности.
Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f (x) – первую производную от функции распределения F (x):
f (x) =  .
.
Зная плотность распределения f (x), можно найти функцию распределения F (x) по формуле
F (x)=  ,
,
Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b:
 или
или 
Геометрически полученный результат можно истолковать так: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью Ох, кривой распределения f (x) и прямыми x=a и x=b.
Плотность распределенияобладает свойствами
Свойство 1. Плотность распределения – неотрицательная функция:
f (x)  .
.
Свойство 2. Несобственный интеграл от плотности распределения в пределах от 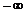 до
до  равен единице:
равен единице:
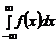 =1.
=1.
Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью Ох и кривой распределения, равна единице.
В частности, если все возможные значения случайной величины принадлежат интервалу (a, b), то
 =1.
=1.
Пример 3.1. Задана плотность распределения вероятности случайной величины Х
f (x)= 
Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5; 1).
Решение. Искомая вероятность
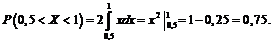
Пример 3.2. Найти функцию распределения по данной плотноcти распределения:
 0 при
0 при  ,
,
f (x)= 1/(b-a)при  ,
,
0 при  .
.
Воспользуемся формулой F (x)= 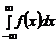 . Если
. Если  , f (x)=0, следовательно, F (x)=0. Если
, f (x)=0, следовательно, F (x)=0. Если  , то f (x)= 1/(b-a), следовательно, F (x)=
, то f (x)= 1/(b-a), следовательно, F (x)= 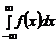 =
= 
 =
=  .
.
Если x > b, то F (x)= 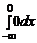 +
+ 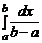 +
+  =
=  .
.
Итак, искомая функция распределения
 0 при
0 при  ,
,
F (x)= (x-a)/(b-a)при  ,
,
1 при 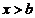 .
.
Пример 3.3. Случайная величина Х подчинена закону распределения с плотностью f (x), причем
f (x)= 
Требуется: 1) Найти коэффициент a; 2) построить график распределения плотности у = f (x); 3) найти вероятность попадания Х в промежуток (1,2).
Решение. 1) Так как все значения данной случайной величины заключены на отрезке[0,3], то  , откуда
, откуда
 или
или 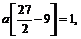 т.е. a = 2/9.
т.е. a = 2/9.
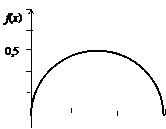 2) Графиком функции f (x) в интервале[0,3] является парабола
2) Графиком функции f (x) в интервале[0,3] является парабола  , а вне этого интервала графиком служит сама ось абсцисс (рис. 4).
, а вне этого интервала графиком служит сама ось абсцисс (рис. 4).
3)Вероятность попадания
случайной величины Х в про-
 межуток (1,2) найдется из ра-
межуток (1,2) найдется из ра-
венства

Задачи для самостоятельного решения
1. Задана плотность распределения вероятностей случайной величины Х
f (x)= 
Найти значение параметра a и определить вероятность попадания случайной величины на интервал (3,4).
2. Задана плотность распределения вероятности случайной величины Х: f (x)= cos x при х 
 [0,
[0,  вне этого интервала плотность распределения вероятностей равна нулю. Найти функцию распределения.
вне этого интервала плотность распределения вероятностей равна нулю. Найти функцию распределения.
3. Случайная величина Х задана в интервале (-2,2) плотностью вероятностей f (x)=1/4; вне этого интервала f (x)=0. Найти вероятность того, что в результате трех независимых испытаний случайная величина ровно два раза попадет в интервал (1,2).
Ответы: 1. a =3/64; p (3  x
x  4)=0,2969. 3. р= 0,140025.
4)=0,2969. 3. р= 0,140025.



 .
. , если
, если  .
. .
.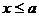 ;
; .
.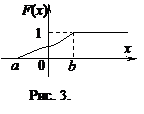
 F (x)=0;
F (x)=0;  F (x)=1.
F (x)=1. .
. ,
, или
или 
 .
.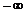 до
до  равен единице:
равен единице: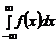 =1.
=1. =1.
=1.
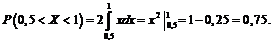
 0 при
0 при  ,
, ,
, .
. , то f (x)= 1/(b-a), следовательно, F (x)=
, то f (x)= 1/(b-a), следовательно, F (x)= 
 =
=  .
.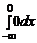 +
+ 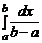 +
+  =
=  .
. 0 при
0 при  ,
, ,
,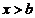 .
.
 , откуда
, откуда или
или 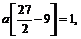 т.е. a = 2/9.
т.е. a = 2/9.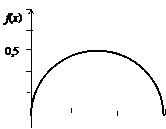 2) Графиком функции f (x) в интервале[0,3] является парабола
2) Графиком функции f (x) в интервале[0,3] является парабола  , а вне этого интервала графиком служит сама ось абсцисс (рис. 4).
, а вне этого интервала графиком служит сама ось абсцисс (рис. 4).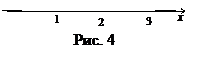 межуток (1,2) найдется из ра-
межуток (1,2) найдется из ра-


 [0,
[0,  вне этого интервала плотность распределения вероятностей равна нулю. Найти функцию распределения.
вне этого интервала плотность распределения вероятностей равна нулю. Найти функцию распределения. x
x 


